小井沟水库围堰溃决洪水演进预测分析

李先明，王占军

（1.中国水务投资有限公司，北京 100053；2.南京水利科学研究院 大坝安全与管理研究所，江苏 南京 210029）

水库大坝 （围堰）溃决后破坏性极大[1]，往往带来巨大的生命财产损失和生态环境破坏。因此，预测分析水库大坝 （围堰）溃决洪水演进过程，可采取工程措施提前切断洪水传播路径或采取非工程措施减少洪水对下游的损害[2]，对防洪减灾具有重要意义。鉴此，本文选用适宜的高精度二维溃坝数学模型，计算施工围堰在遭遇超标洪水时漫顶造成围堰溃决后二维溃坝洪水演进过程，以期提高小井沟水库工程对施工期间洪涝灾害或突发紧急情况的应急反应能力。

1 工程概况

小井沟水库位于岷江左岸一级支流越溪河干流上。越溪河流域水系呈羽状分布，干流全长239 km，河道纵坡比降0.18%，流域面积2667 km2。水库正常蓄水位429.00 m，100年一遇设计洪水位429.00 m，2000年一遇校核洪水位430.75 m。水库总库容1.6595亿m3，为Ⅱ等大 （2）型工程。大坝为混凝土面板堆石坝，最大坝高87.6 m，坝顶宽8.0 m。上游围堰为土石围堰，堰顶高程381.50 m，顶宽10.0 m，上、下游边坡坡比均为1∶1.8。下游围堰为粘土心墙土石围堰，顶高程353.50 m，顶宽6.0 m。围堰迎水面和背水面坡度均为1∶1.5。

2 围堰溃决分析

2.1 溃决主要因素分析

根据小井沟工程自然条件及枢纽布置特点，施工期上游围堰采用土石围堰，溃决主要因素如下:

（1）超标准洪水。按照小井沟工程2012年度度汛方案，围堰施工期间如遇水位迅速上涨，在水位接近填筑面2.0 m且继续上涨趋势时，拟在围堰填筑面上游侧抢修一道宽1 m、高2 m的编织袋装土(编织袋内装防渗土料)临时挡水子堰，防止洪水漫堰。但遇超标准水位，上游水位持续快速增长，则可能会引起围堰溃决。

（2）人工破堰。如水位继续上涨，拟在水位接近编织袋挡水堰顶高程0.5 m且有继续上涨趋势时，采取破堰处理，人工破堰可能引起围堰溃决。

（3）工程质量。就一般土石围堰而言，若存在施工质量问题，则可能出现由工程质量差引起的溃决，如管涌等。考虑到本工程的施工围堰在上游侧敷设复合土工膜1层，且复合土工膜嵌入两侧岸坡防渗槽内，宽40 cm，防渗槽内设φ22，L=1.5 m锚杆，注M20砂浆，锚入岸坡基岩1 m，伸入混凝土内50 cm，插筋2排，间距1.5 m；土工膜两侧喷20 cm厚C20混凝土；下部与戗堤粘土斜墙相接；则该围堰因管涌引起的溃决的可能性较小。

故，本次溃决分析选择超标准洪水引起的溃决。

2.2 溃决方式及溃口流量过程计算

根据小井沟枢纽设计洪水成果5%洪峰流量990 m3/s，调洪计算成果显示，相应的库水位分别为388.7 m，已经超过382.0 m。根据设计条件，当水位上升至382 m高程且有继续上升趋势时，采取破堰措施。为安全考虑，此时上游围堰破堰为爆破形式，形成的溃坝洪水采用全溃的方式进行计算，且溃决时不利时机为同时遭遇洪水洪峰时。

由于围堰下游坡度大，基本为急流，可以按照下游水位流量关系计算坝下水位。根据宽顶堰出流公式[3]计算所得溃口流量过程如图1所示。

图1 上游围堰如溃决其溃口流量过程

3 溃坝洪水演进模型及其验证

为安全起见，考虑研究小井沟水库施工围堰在遭遇超标洪水时漫顶造成围堰溃决后溃坝洪水波演进过程。施工围堰溃坝洪水演进的区域大部分位于山谷，该山谷底坡大且蜿蜒曲折，有大洪水取直的可能，选用适宜的高精度二维溃坝数学模型计算，以更好地了解溃坝洪水演进过程及产生的危害。

3.1 基本方程

连续方程

动量方程

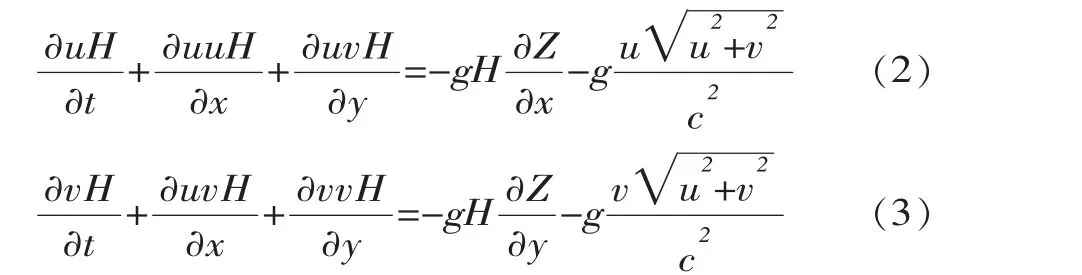
式中，H、Z为水深和水位，m；u、v为x、y向的流速，m/s；ρ为水体密度，kg/m3；c为谢才系数。

3.2 定解条件

（2）边界条件:上游边界以溃决流量作为其边界条件，下游采用无反射边界条件。

3.3 数值方法

为保证良好的计算精度，采用二阶FDS格式的有限体积法计算二维溃坝洪水演进过程。

3.4 计算区域及网格

溃坝洪水演进计算区域应包含主要敏感点及洪水出路。本工程主要敏感点主要为施工围堰下游山谷旁的村庄、零散民居等。故，计算区域包括施工围堰以下至征远村的380 m等高线以下所有区域。采用三角形网格剖分，共布置计算节点90855个，控制单元174276个。由于山谷狭窄，地形变化大，网格采用均匀间距20 m布置 （见图2）。

图2 计算区域及网格布置

3.5 计算参数

本模型计算参数根据工程实际情况并参考以往研究资料确定。主要参数为糙率n，由于该工程溃坝洪水演进水流流势急，大部分为急流，该参数不敏感。根据工程附近的实际情况，山谷糙率采用0.028～0.036，河道糙率取0.026。溃坝洪水水流湍急，非线性特性极强，模型计算时间步长取0.01 s。

3.6 模型验证

模型验证计算采用二维、平底、无摩阻、局部溃坝问题。模拟区大小为200 m×200 m，初始坝址水位为10 m，相应坝下水位为5.0 m。溃坝缺口为75 m宽 （见图3），溃决瞬间形成一激波向下游传播同时有一负波向上游扩散。计算区划分为40×40个矩形单元，计算时步长为0.2 s。溃坝7.2 s后与基于N-S方程的三维模型模拟结果以及Fennema和Chaundry的计算结果进行了对比验证 （见图4和图5）。验证结果表明，本模型可满足计算要求。

4 淹没范围预测分析

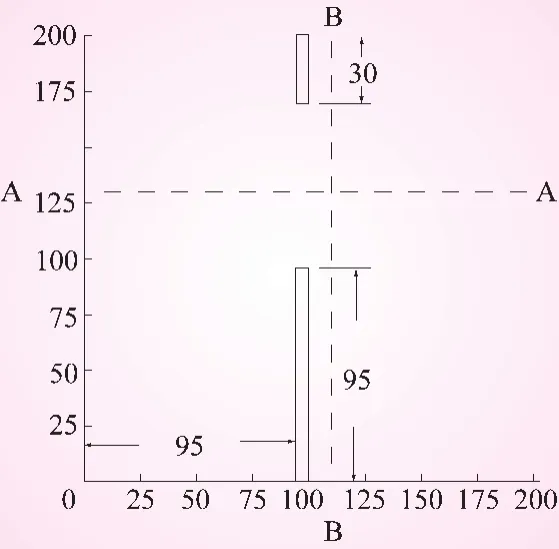
图3 溃坝验证计算区域

图4 溃坝7.2 s后与三维模型水面对比

图5 溃坝7.2 s后典型断面水深对比

由溃坝洪水演进数值模拟得到20年一遇洪水条件下围堰溃决时溃坝洪水演进水深等值线过程 （见图 6）。

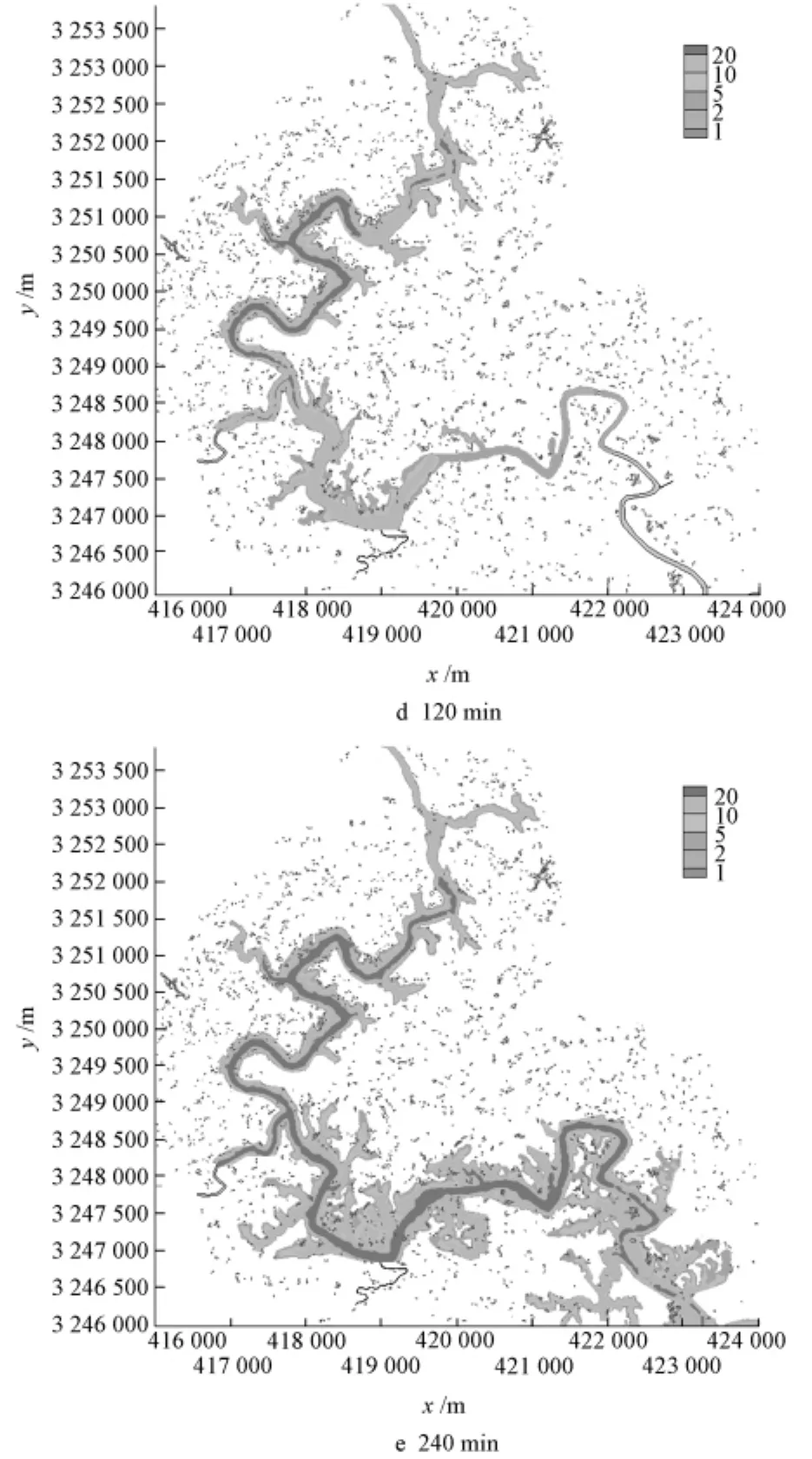
图6 遭遇20年一遇洪水溃决时洪水演进淹没水深过程

图6中，x、y分别为纬、经度方向的坐标。溃坝洪水的模拟时间为溃坝后4 h，其间天然洪水洪量约1406万m3，上游围堰水位达到382.00 m时库容约1200万m3，合计溃坝洪量约2606万m3。计算得4 h溃坝洪水约向下游演进29.5 km，平均演进速度2.0 m/s，按平均水面宽100 m计算，平均水深约8.7 m。

由图6可以看出，该工程下游底坡陡，河谷狭窄，槽蓄量不大，造成的溃坝洪水具有演进快、水深大的特点。遭遇20年一遇洪水围堰溃决时下游4 h后最大淹没水深显示 （见图6e），围堰溃决时下游有较多的民房将被冲毁，但只要破堰前提前组织民众撤离，能有效避免人员伤亡。

5 结语

本文选用高精度二维溃坝数学模型，计算了小井沟水库施工围堰遭遇超标洪水时漫顶造成围堰溃决后二维溃坝洪水演进过程，得到20年一遇超标准洪水条件下围堰溃决时溃坝洪水演进水深等值线。4 h溃坝洪水约向下游演进29.5 km，平均水深约8.7 m，围堰溃决时下游有较多的民房将被冲毁。但只要破堰前提前组织民众撤离，能有效避免人员伤亡、减少下游损失。

［1］解家毕，孙东亚.全国水库溃坝统计及溃坝原因分析［J］.水利水电技术， 2009， 40（12）:124-128.

［2］黄凌，孙月峰，李颖.水库溃坝洪水数值模拟与防洪管理对策研究［J］.天津大学学报: 社会科学版， 2011， 13（2）:116-120.

［3］吴持恭.水力学［M］.3版.北京:高等教育出版社，2003.