市场环境下梯级水电站短期优化调度研究

徐 刚

（三峡大学水利与环境学院，湖北 宜昌 443002）

0 引言

市场经济条件下，由于市场竞争，电价和电量均存在不确定性。在此情况下，制定梯级水电站短期优化调度计划分为竞价阶段和负荷分配执行阶段。每个阶段有其个自不同的优化调度目标。竞价阶段，梯级水电站根据当前水情和市场情况，报送时段价格及出力计划至电网交易中心，其短期优化调度计划主要目的是发电收入最大化。负荷分配执行阶段，梯级水电站根据电网下达的负荷要求进行厂间负荷分配，在流域梯级统一电价前提下短期优化调度计划主要目的为发电耗水量最小；若流域梯级水电站具有不同电价，则目标设定为梯级发电收入最大。研究不同阶段采用不同的优化调度模型和算法，对流域梯级水电站合理制定梯级短期发电计划、增加梯级水电站发电效益、节约梯级水资源具有积极意义。

目前，国内外对于梯级短期优化调度方面的研究主要有纪昌明等[1]、李安强等[2]、谢红胜等[3]、宋洋[4]、 杨道辉[5]、 陈立华[6]、 Nenad Tufegdzic[7]、 Xiaohui Yuan等[8]、J.P.S.Catal等[9]各种模型及方法。在这绝大部分文献中，忽略或没有明确说明梯级短期优化调度各阶段具有不同特点，在当前电力市场条件下，特别是在面临日前96点电价和负荷情况下，在高维数、强约束条件下，上述文献模型或方法没有针对各阶段特点形成整体解决框架方案予以应用。本文探讨如何根据不同阶段特点建立优化调度模型，继而进行优化求解，构建可靠的求解算法；进而希望为梯级水电厂短期梯级优化调度问题构建整体解决框架提供进一步思路。

1 短期优化调度模型

1.1 市场竞价阶段模型

已知电网次日96点边际电价，梯级各水电站水库初末水位，求各站的96点时段出力，使调度期内梯级水电站总的发电收入最大。目标函数

约束条件:

水量平衡约束

水库蓄水量约束

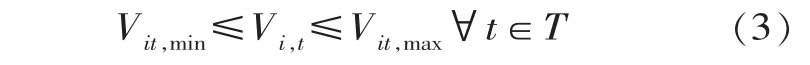
水库下泄流量约束

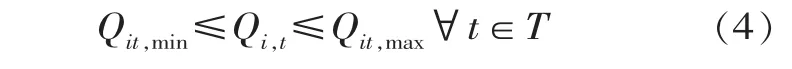
水电站出力约束

式中，J为梯级水电站控制期内发电收入；Ai为第i个水电站综合出力系数；pt为t时段预测系统边际电价；Qi，t为第i个水电站在t时段发电流量，m3/s；Hi，t为第i个水电站在t时段平均发电净水头，m；T为日内计算总时段 （计算时段为日，T=96）；Mt第t时段小时数 （0.25 h）， h； Vi，t+1为第 i个水电站第 t时段末水库蓄水量，m3；Vi，t为第i个水电站第t时段初水库蓄水量，m3；qi，t为第i个水电站第 t时段平均入库 （区间）流量， m3/s； qi-1，t-τ为第 i-1个水电站第t-τ时段平均下泄流量 （τ为流达时间），m3/s； Si，t为第 i个水电站在 t时段弃水流量， m3/s； Vi，t，min为第i个水电站第t时段应保证的水库最小蓄水量，m3； Vi，t为第 i个水电站第 t时段水库蓄水量， m3；Vi，t，max为第 i个水电站第 t时段允许的水库最大蓄水量， m3； Qi，t，min为第 i个水电站第 t时段应保证的最小下泄流量， m3/s； Qi，t，max为第 i个水电站第 t时段允许的最大下泄流量，m3/s；Ni，min为第i个水电站允许的最小出力，MW；Ni，max为第i个水电站的最大出力限制，MW。

1.2 负荷分配阶段模型

在流域梯级统一电价背景下，目前常用的是经济运行模型为考虑启停费用的耗水量最小模型。它是指已知梯级各水电站初始水位和调度期内负荷曲线，求梯级水电站在调度期内的最优出力过程，使耗水量达到最小。目标函数

目前，机组启停费用没有统一的标准，通常是将其等价为机组满带负荷3～5 min内消耗的水量[1]。

若流域各水电站具不同电价，则考虑采用满足负荷分配要求下发电收入最大化模型，目标函数

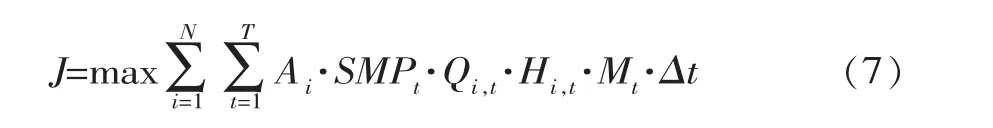
约束条件:

动力 （负荷）平衡约束

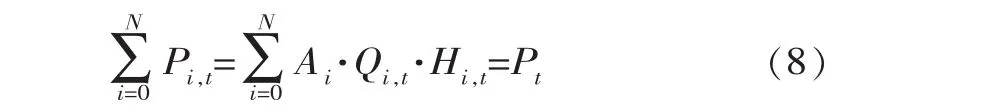
水量平衡约束

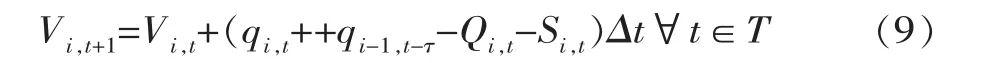
水库蓄水量约束

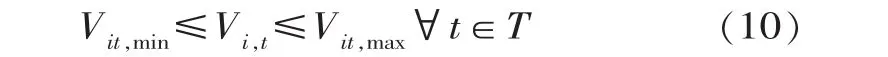
发电流量约束

水电站出力约束

式中，F为梯级水电站总耗水量，m3；SMPt为t时段系统边际电价；Pi，t为第i电厂第t时段内的出力，MW；Pt为系统在第t时段内对梯级总出力要求，MW ；Qsi，t为第i个水电站在t时段启停流量，m3/s（无启停则该项为0）。

2 求解算法模型

目前， 市场竞价阶段常用的模型求解算法[1，3，5]的基本原理是:定义水库调度线为求解路径，利用逐步调整、状态转移、信息素更新和邻域搜索等方法，调整路径逐步向最优值逼近，求解全局最优解。

本文针对梯级厂间负荷分配模型提出层次化负荷分配算法。为了保证求解可靠性，进行结构化分层，将算法划分为初始可行解的构建和优化解求解两个层次。其中，初始可行解采用随机负荷分配算法，在初始可行解基础上采用负荷微增逐次寻优算法，寻求最优解。以发电收入最大化模型为例。

2.1 厂间负荷随机分配算法

算法原理:为了满足动力平衡约束，采用梯级水电站出力作为决策变量，确定逐级水电站的出力后，利用出力反推发电流量算法反推出各级水电站发电流量，进行水量平衡计算，确定各级水电站水位、库容等状态变量。步骤如下:

（1）给定初始水位，从第1时段开始逐时段分配负荷，按梯级水电站数目利用随机数生成分配出力 Pi，t（i=1，…，N）， 总和为梯级时段总负荷 Pt。

（2）从梯级第1级水电站开始，利用出力反推流量算法，进行试算求解对应出力P1，t的发电流量Q1，t；进行水量平衡计算，得到时段末水位、库容，若出力过大，水量平衡将不能满足则回到步骤1。

（3）将上一级水电站下泄流量加上本级水电站区间流量作为入流，按步骤（2）以同样方式计算本级水电站发电流量和时段末水位、库容，进行水量平衡校核；计算至梯级最后一级水电站。

（4）比较最后一级水电站分配负荷PN，t与实际可发出力 P′N，t， 若差别过大 （＞1%）， 表明最后一级水电站可能发生弃水，本时段梯级负荷分配方案不合理，回到步骤1重新分配该时段各梯级负荷Pi，t。

（5）至此一个时段负荷分配完毕，各梯级水电站时段末水位、库容状态也以确定，回到步骤1开始分配下一时段，计算至最后一个时段结束，得到1 组梯级厂间负荷分配可行解 Pi，t（i=1，…，N）。

（6）反复运算多次得到多组可行解，作为下一层次优化求解算法基础。

2.2 负荷微增逐次寻优算法

算法原理:对每组可行解，任意挑选其中两个水电站负荷进行一正一负微增量调整操作，以保证时段总负荷不变，比较调整前后梯级总发电收入，逐次迭代调整直至梯级发电收入收敛。算法步骤:

（1）对每一组可行解 Pi，t（i=1，…，N）进行出力微增操作计算； 任意挑选其中两个水电站负荷Pl，N、Pj，N（j≠l）， 对水电站负荷 Pl，N增加一个微小负荷△P、Pj，N相应减少负荷△P。

（2）对受到负荷调整影响的每个时段及水电站进行负荷调整计算 （出力反推和水量平衡计算），得到负荷调整后相应的发电流量及时段末水位、库容。

（3）计算比较调整前后的目标函数即总发电收入，保留使得发电收入增大的负荷调整方案P′i，t（i=1，…，N）作为新的梯级负荷分配优化解。

（4）对每组可行解进行以上步骤的出力微增操作；挑选所有负荷分配方案中发电收入的最优值，完成一次迭代。

（5）逐次迭代，直至发电收入目标函数收敛，该收敛目标可以为两次迭代值之差小于设定阈值，也可以为预设的迭代次数。

该层次化负荷分配算法首先以梯级水电站出力为决策变量，满足负荷平衡，同时通过出力反推流量计算和水量平衡计算满足水量平衡，以此保证初始解的可行性；其次进行出力微增调整，进行逐次迭代，根据逐次优化原理，逼近最优解。

3 实例计算

本研究以金沙江左岸一级支流西溪河流域梯级水电站为例。该梯级目前已建成洛古、联补、地洛等三个水电站，洛古为季调节水电站，联补、地洛为日调节水电站，联补、地洛水电站水库有区间入流汇入。已知梯级入流量，区间来水量，梯级电站间流达时间，预测的系统边际电价为:0:00－6:30为144.5元/MW，6:45－10:30为 385.8元/MW，10:45－13:30为 289元/MW，13:45－18:15为 385.8元/MW，18:30－23:45为144.5元/MW。给定洛古、联补、地洛水电站日开始水位分别为2041、1674、1217 m，日结束水位分别为2041、1674、1217 m作为计算初始条件。求竞价阶段梯级水电站短期优化调度计划使得梯级发电收益最大 （见图1，图2）。

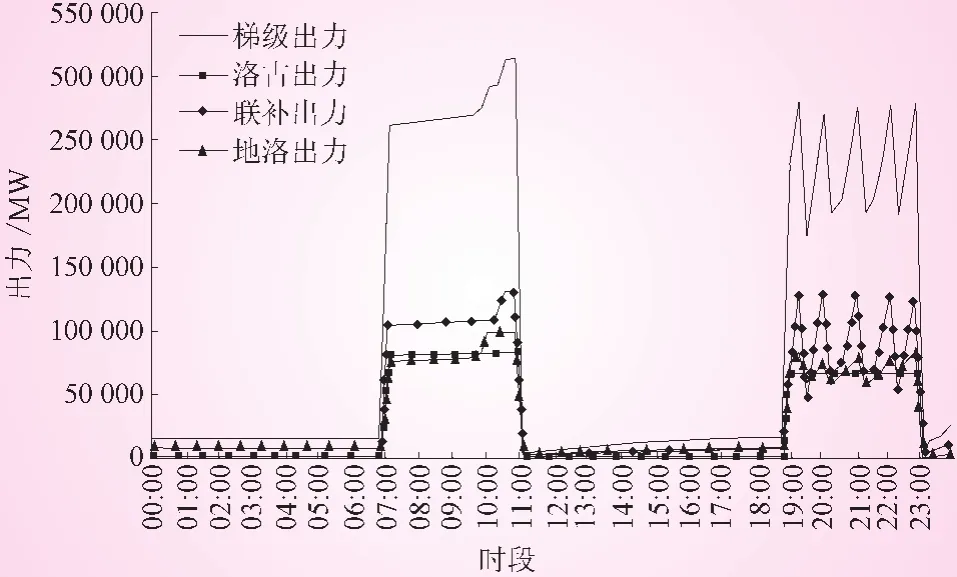
图1 梯级各水电站出力过程

图2 梯级各水电站水位过程

表1 层次化负荷分配算法不同目标结果对比

分析图1、图2可看出，各水电站间水位变化过程相互对应，均在高电价时段加大下泄，低电价时段蓄水；同时，洛古水电站发挥了龙头水库的优势，通过水库蓄放，调配更多的水量在联补、地洛水电站高电价时段发电。图1中高电价时段梯级明显多发电，且时间与边际电价时段对应，梯级发电效益相应增大，可见模型和算法求解结果是合理的。

在负荷分配阶段，若电力系统下达的日负荷为:0:00-6:30为150 MW，6:45-10:30为200 MW，10:45-13:30为150 MW，13:45-18:15为200 MW，18:30-23:45为150 MW。为比较起见，梯级耗水量最小为目标时，设各时段流域统一电价为相应时段系统边际电价，具体值同前面预测值；梯级总发电收入最大为目标时，设各时段洛古、联补、地洛电价为各自枯水期峰、平、谷段电价。给定洛古、联补、地洛水电站日开始水位分别为2041、1674、1217 m作为计算初始条件，求不同的梯级水电站厂间负荷分配方案分别使梯级总耗水量最小、总发电收入最大2个不同目标。

利用梯级水电站间负荷分配算法分别求解出梯级耗水量最小化和发电收入最大化时的洛古、联补、地洛水电站及梯级总的发电量、发电收入和耗水量见表1。

由表1可以看出，求解的各水电站出力时段之和等于电网下达的时段梯级负荷要求，达到了负荷分配目的。耗水量最小化与发电收入最大化目标求解结果比较，在完成电网下达的负荷要求前提下，洛古耗水量前者较后者减少0.5%。追求耗水量最小化目标设定为所有梯级水电站耗水量最小，从出力过程线看显著增加了启停次数，出力变化过于频繁，故该目标制定的出力分配方式虽然较优，但不实用。发电收入最大化目标使具有较高电价的洛古水电站多发电，并且出力过程较为均匀，故推荐该目标函数制定的负荷分配计划。在采用不同目标进行优化后，可以增加发电收入、节约水资源。结果表明，层次化负荷分配算法求解结果合理有效。

根据上述模型和算法，研究构建了基于Web的梯级水电站调度决策支持系统。系统为梯级短期优化调度提供了一个有效的整体解决框架，为竞价前和下达负荷不同阶段、不同方式下梯级短期优化调度提供了决策支持。

4 结语

本文通过对梯级水电站短期优化调度整体框架的研究，以节约梯级水资源、增加梯级发电收入为目的，建立不同阶段下梯级优化调度模型，针对不同模型提出求解算法。实例验证表明，算法解决了高维、多约束条件下梯级短期优化调度问题。研究为梯级短期优化调度整体解决框架提供了一个思路。研究在模型构建过程中将梯级水电站概化为单一机组，未进一步深入结合厂内机组经济运行研究，有待今后工作中继续深入及完善。

［1］纪昌明，张玉山，李继清.市场环境下水电系统厂间经济运行问题研究［J］.华北电力大学学报， 2005， 32（1）:99-102.

［2］李安强，王丽萍，蔺伟民，等.免疫粒子群算法在梯级水电站短期优化调度中的应用［J］.水利学报， 2008， 39（4）:426-432.

［3］谢红胜，吴相林，陈阳，等.梯级水水电站短期优化调度研究［J］.水力发电学报， 2008， 27（6）:1-7.

［4］宋洋，钟登华，钟炜，等.面向电力市场的梯级水水电站联合优化调度研究［J］.水力发电学报， 2007， 26（3）:22-28.

［5］杨道辉，马光文，杨梅.育种粒子群算法在梯级水水电站优化调度中的应用［J］.水力发电学报， 2010， 29（1）:207-212.

［6］陈立华，梅亚东，杨娜.自适应多策略粒子群算法在水库群优化调度中的应用［J］.水力发电学报， 2010， 29（2）:139-143.

［7］TUFEGDZIC N,HYSLOP P.An optimal real-time short term operation of independent hydro generator company in the open electricity market［J］.Electric Power Systems Research,1997， 41（1）:5-11.

［8］YUAN Xiaohui,WANG Liang,YUAN Yanbin.Application of enhanced PSO approach to optimal scheduling of hydro system ［J］.Energy Conversion and Management,2008,49（11）:2966-2972.

［9］CATALAO J P S,POUSINHO H M I,MENDES V M F.Mixed-integer nonlinear approach for the optimal scheduling of a head-dependent hydro chain［J］.Electric Power Systems Research.2010,80（8）:935-942.