基于有限元法的流体与结构的耦合研究

赵大为

（中国舰船研究设计中心， 湖北 武汉430064）

基于有限元法的流体与结构的耦合研究

赵大为

（中国舰船研究设计中心， 湖北 武汉430064）

对有限元法离散流固耦合方程进行了简要的介绍，给出了粘性流体与弹性结构的全耦合模型。流体采用k-ε湍流模型进行了有限元计算，采用ALE描述实现固体Lagrangian描述到流体Eulerian描述的过渡，使大变形带来的流体域网格畸变得以避免。对流固耦合方程，采用流固全耦合的迭代算法进行了迭代求解，最后模拟了高雷诺数下湍流流动中冲击致使涡轮结构旋转的过程。计算结果表明，流固耦合的算法是可靠的。

有限元法(FEM)；流体冲击；流固耦合

0 引言

在海洋工程领域中，都会遇到流体和结构的相互作用问题，简称为流固耦合问题。流固耦合力学的重要特征是两相介质间的交互作用，即固体在流体载荷作用下会产生变形或运动，而变形或运动反过来又影响流场的流动，从而改变流体载荷的分布和大小。一般流固耦合的特点是方程的定义域同时有流体域和固体域，未知变量既有流体变量又有固体变量，而且流体域和固体域通常无法单独求解。

从总体上看，按照耦合机理流固耦合问题可以分为两大类。第一类是两相域部分或全部重叠在一起，很难明显地分开，使描述物理现象的方程，特别是本构方程需要针对具体的物理现象来建立，其耦合效应通过描述问题的微分方程而体现，如渗流问题。第二类问题的特征是耦合作用仅发生在两相交界面上，在方程上耦合是由两相耦合面的平衡及协调关系引入的。Zienkiewcz和Bettess[1]曾将上述第二类流固耦合问题分为三种情况，一是流固间有大的相对运动情况，如飞机飞行状态下的气动弹性力学问题；二是有限流体运动的短周期情况，如流体受冲击和水下爆炸问题；三是有限流体位移的长周期情况，如含液容器的流固耦合振动问题。

1 流固耦合的分析方法

流固耦合问题的历史可以追溯到 1843年，当时Stokes[2]研究了一个无限长圆柱体在无限流体介质中的均匀加速问题。他得出的结论是：流体对圆柱体运动仅有的影响是增加了它的有效质量。Stokes早年的这种引入附加有效质量的基本概念和做法极大地影响了流固耦合分析理论后来的发展。

现代流固耦合分析开始于20世纪50年代。最早进行航天运载器中液体燃料容器的分析研究，而对于核动力系统，最著名的是Fritz和Kiss[3]关于同心圆柱体摆动运动的研究报告，其中流体介质是有限的，固体是刚性体。

自20世纪70年代以来，人们开始研究流体与弹性体间的流固耦合问题。最早的论文是Krajcinovic在1974年发表的。早期的流体-结构耦合分析一般是以核反应堆安全分析为背景的，Belytschko在1977年对这一阶段进行了总结[4]，指出当时的耦合分析实际是以解耦的方式进行的，即：首先，忽略结构变形，将结构看作流体的刚性壁，计算流场分布；然后，将流体计算得到的刚性壁压力加在结构上，计算结构的变形、响应。一般认为，流场作用于刚性壁的压力比柔性壁要大，所以结果对结构来说是趋于保守的。这种解耦算法一方面导致结构的过于安全的设计；另一方面，当流体—结构系统发生共振时，这种算法是不可信、不安全的。正是因为采用解耦的算法，流体域可以采用有限元，也可以采用有限差分。

在随后的三十多年中，由于计算固体力学、计算流体力学的不断发展完善以及计算经验的不断积累，最初的分析方法不再被采用。耦合的算法取代了解耦算法，因为有限差分与有限元联合计算有很大困难以及有限元在流场计算中的不断完善，有限元成为流体—结构耦合的主导算法。

2 标准k-ε湍流模型的封闭方程组

Reynolds首先认为流体的运动在从层流状态过渡到湍流状态后，流体的物理和力学性质没有变化，流体的连续性没有受到破外，Navier-Stokes方程仍能描写湍流的瞬时规律。上述假定虽然至今仍未能得到严密论证和证实，但一百多年以来，研究湍流的实践表明，这些假定并没有与实际情况发生矛盾，说明Navier-Stokes方程应用于湍流问题是适宜的。如用f表示流动变量的瞬时值，表示f的统计平均值，各量的瞬时值与统计平均值之差即为各量大的脉动值 ′，即：

根据式(1)，将连续方程、动量方程平均化后得(为符号简单起见，平均值速度u、压力p符号上的“-”都去掉了)。

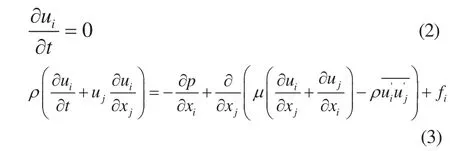
方程(3)首先由Reynolds于1895年导出，因而通常称为 Reynolds方程。其中称为Reynolds应力。 方程(2)、(3)中只有缓变的平均值，故消除了因脉动而引起的不规则变化，使方程便于应用。由于方程中出现了许多新项，又产生了新的困难。方程中未变量的个数多于方程个数，因而是不封闭的，必须在试验资料基础上做出一些假设，建立补充关系后才能求解。对雷诺应力采用与层流类似的模型，可将其表示为：

式中， 为湍流粘性；k为湍流脉动动能的平均值；在式(4)中引进了两个未知量 和k，为了封闭还要求两个方程。对于大Reynolds数流动，由量纲分析可得：

式中，ε为脉动动能的耗损速率。关于k和ε的精确方程可有Navier-Stokes方程和Reynolds方程导得，对其中的各项进行分析和某些假设(模式化)后，可以得出能量输运方程：

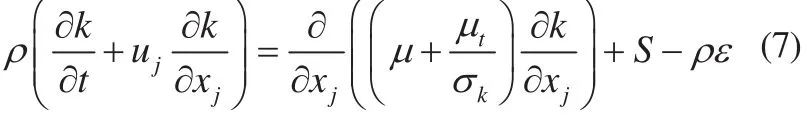
方程式中的S为脉动流在单位时间内通过 Reynolds应力从平均流所获得的能量：

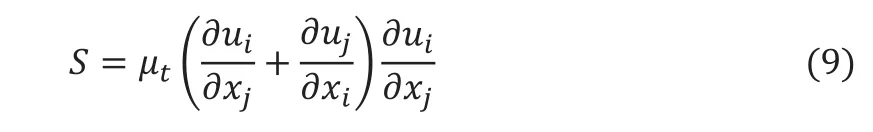
式中， 、 、 、、为经验常数，对标准模型，Spalding和 Launder[4-5]建议分别取0.09、1.00、1.30、1.44、1.92。

上述方程组成了标准的k-ε湍流模型的封闭方程组。

3 流固耦合系统的方程

ALE描述实际只是与物质时间导数相关，反映了物理量时间上的绝对变化和相对变化的关系，从而容易得到N-S方程的ALE描述形式如下：

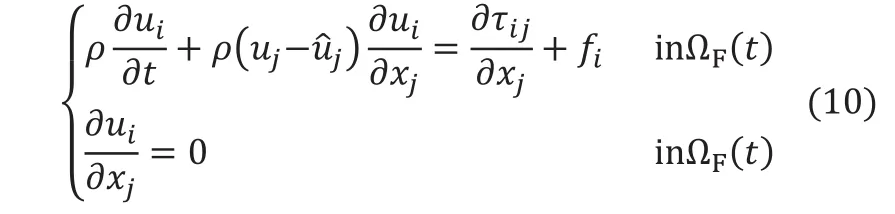
从式(10)可以看出，ALE描述并不影响空间导数项。针对边界问题，相当于调整网格后，使对原问题的描述既不是Lagrangian描述，也不是Eulerian描述，调整网格引入的对流量 也必须考虑在内。

根据公式(10)，ALE描述的k-ε湍流模型封闭方程组可写为：

4 迭代法求解双向耦合

在很多耦合问题中，流体的作用力影响结构的变形，同时结构的位移又影响流场的形态。这正是进行流固耦合分析的原因，这种类型的分析叫做“双向耦合(two-way coupling)”。在某些情况下，结构的变形非常小，它对流体的影响可以忽略。只有流体的应力需要施加到结构上，流体和结构模型之间不需要迭代，这种类型的耦合叫做“单项耦合(one-way coupling)”。

迭代法求解双向耦合的解法也叫做分离法。流体和结构的求解变量是完全耦合的。流体方程和结构方程是按顺序相互迭代求解的，各自在每一步得到的结果提供给另一部份使用，直到耦合系统的解达到收敛，迭代停止。

计算过程可以概括为：为了得到t+Δt时刻的解，在流体模型和结构模型之间开始迭代计算。设初始解为：。对迭代步k=1，2，··，进行下面的求解过程以得到(t+Δt)X。

2)如果只需要满足应力收敛条件，则只要计算应力残量并与迭代容差相比较。如果这个标准满足了，以下3)到5)步骤就可以忽略了。

5)如果只需要满足位移收敛条件，则要计算位移残量并与迭代容差相比较。如果应力和位移的标准都要求满足，则两个收敛条件都要检查。如果迭代不收敛，回到第1)步继续下一个迭代，直到达到FSI迭代的最大数。

6)保存并输出流体和结构的结果。在这种求解方法中，时间步和求解时间是由流体模型控制的。然而，结构模型中定义的所有时间函数必须覆盖计算的时间范围。耦合系统最终控制收敛的参数是由流体模型决定的。这些参数包括应力和位移迭代容差，松弛因子，收敛标准等。流体和结构模型的收敛分别由各自的方程控制。保存和输出解也同样由各自的模型控制。

5 算例

此算例模拟在湍流流体作用下致使结构旋转，流体模型仍然为k-ε湍流模型。如图1所示，开始分析时，涡轮是静止的。在涡轮入口处突然施加一个入口边界的压力，流体流过涡轮箱，使涡轮旋转。

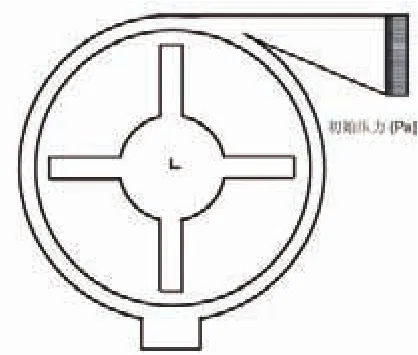
图1 几何形状和入口条件

各参数取值为：①流体：密度ρ=1000kg/m3，运动粘性系数ν=0.01m2/s，初始压力为P=500Pa。②涡轮：密度ρ=7800kg/m3，弹性模量E=207GPa，泊松比ν′=0.3。

采用滑移网格，时间步长 Δt=0.2s。本问题计算所得的流场压力等值域和速度矢量见图2、3，图2中同时给出了涡轮大幅转动以及应力变化。从图中可以清楚地看到，在施加突然的压力之后，随着涡轮内部流场的变化，涡轮叶片产生了明显的应力变化和转动。

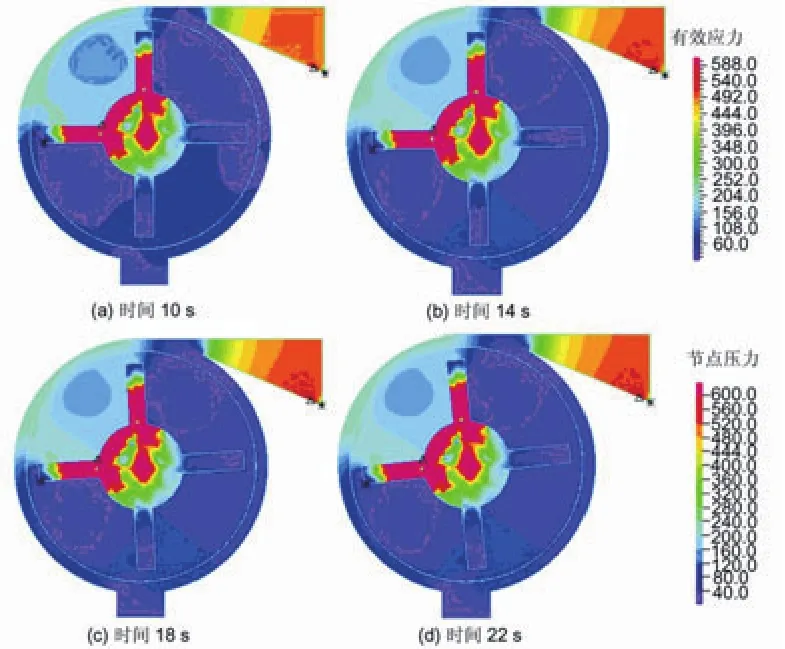
图2 不同时刻流体节点压力云图及涡轮有效应力云图(Pa)

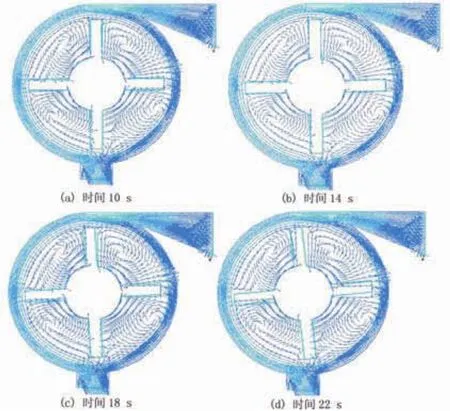
图3 不同时刻速度矢量图

6 结论

上述算例分析了涡轮结构在来流压力作用下的旋转，结构在受来流的冲击开始旋转，从计算结果可以看出，流体的压力能够让流体域中的结构产生运动和变形，涡轮叶片的受力也极不均匀，转动轴心处的应力变化较大。

[1] Zienkiewicz O C, Bettess P. Fluid-structure dynamic interaction and wave forces: an introduction to numerical treatment[J]. Int. J. Num. Meth. Eng.,1978(13): 1-16.

[2] Karamcheti K. Principle of idea-fluid aerodynamics[M]. New York: John Wiley & Sons,1966.

[3] Fritz R J. The effect of liquids on the dynamic motion of solid [J]. J. Eng. Ind., 1972, 94(1):167-173.

[4] Belytschko T. Method and programs for analysis of fluid-structure systems [J]. Nucl. Eng. Des. ,1977,42:41-52.

[5] Launder B E, Spalding B E. Lectures in mathematical models of turbulence[M]. London: Academic Press,1972: 78-115.

Coupling Research of Fluid and Structure Based on Finite Element Method

ZHAO Da-wei

(China Ship Development and Design Center, Wuhan 430064, China)

The process of the fluid-solid coupling equation discretized by finite element method is simply introduced. It also gives the full coupled model of viscous fluid and elastic structure. The finite element calculation of the fluid is carried out by using k-ε turbulence model. Using ALE description achieves the translation from the lagrangin description of solid to the Eulerian description of the fluid to avoid the mesh distortion of the fluid grid caused by the great deformation. Fluid solid coupling equation iterative solution is carried out by using iterative algorithm fluid-solid coupling. Finally, the rotating process of turbine structure caused by turbulent flow impact in high Reynolds number is simulated. The calculation results show that the fluid solid coupling method is reliable.

finite element method (FEM);fluid impact;fluid-solid coupling (FSI)

U664.5+8

A

赵大为(1982-，男，工程师。研究方向：船舶系统。