突发8PSK信号载波同步算法研究
李腾飞,张利锋,方 远
(1.中国电子科技集团第五十四研究所,河北石家庄 050081;2.中国人民解放军63891部队,河南洛阳 471003)
0 引言
调制解调在卫星通信系统中占有非常重要的位置。解调又是调制解调中的关键,解调中的载波同步实现的好坏是解调的关键。在现有的TDMA系统中多采用突发通信,突发信号对解调的载波和时钟捕获时间要求比较高,解调的入锁和同步需要在十几个码元时间内实现。传统的解调器中一般使用科斯塔斯环的方法实现载波同步,但由于会出现“悬隔效应”的问题,不太适用于突发信号的解调。下面针对8PSK突发信号研究基于开环的载波同步方法。
1 模型分析
1.1 开环估计
图1中接收信号在经过中频数字正交下变频分解为基带信号,在完成数字化和A/D采样后,送入匹配滤波器进行滤波,之后送入时钟恢复单元完成码元的时钟恢复,载波频偏和初始相偏由开环相位估计器估计得出。
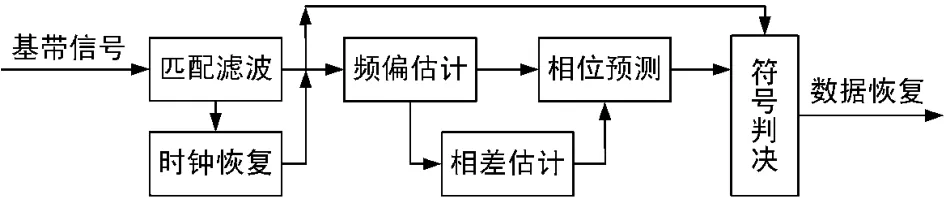
图1 开环结构8PSK解调模型
1.2 相位预测与符号判决
首先对包含载波相差和载波频差的信号进行非线性处理,从而去除调制信号对相位的影响,提取出所需要的载波频偏。
根据载波频偏的估计值和初始相差的估计值消除相位偏差并预测当前相位。在与当前载波相位进行比较判决后输出数据。
2 频偏估计
假设定时恢复理想,则载波恢复的输入信号为:
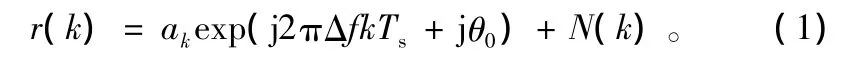
式中,ak为8PSK数据的抽样值;Δf表示本地载波频偏;θ0为相位差值;Ts为采样周期;N(k)=NI(K)+jNQ(k)表示加性复高斯白噪声和因Δf≠0而引入的码间串扰。由于N(k)中码间串扰引起的噪声分量可以忽略不计,N(k)=NI(K)+jNQ(k)可以等效为均值为0、方差为N0/(2Es)=N0/(4Eb)的加性复高斯白噪声,Es为符号能量,Eb为比特能量。通过计算相邻码元的相位差得到频偏估计的大小。
r(k)中的加性噪声在高信噪比条件下可以等效为相位噪声,由文献[3],θ(k)可以表示为:
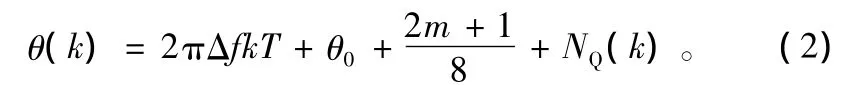
式中,k=-(H -1)/2,……,(H -1)/2;m取0,1,…,7,估计间隔为H*T(H≤N,N是一个突发中的符号数);NQ(k)是均值为零、方差为N0/Eb的等效相位高斯噪声。将θ(k)乘以8以消除调制分量,有
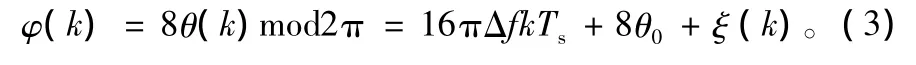
式中,ξ(k)=8NQ(k)mod2π,mod2π表示模2π操作。对φ(k)做差分运算可以得到:
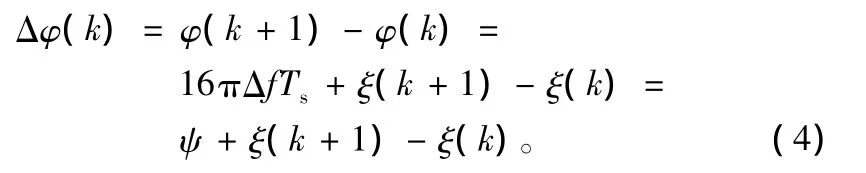
式中,k=-(H -1)/2,……,(H -3)/2;ψ =16πΔfTs。从式(4)中可以明显看出,想要得到Δf的估计值,估计出均值ψ就可以了:
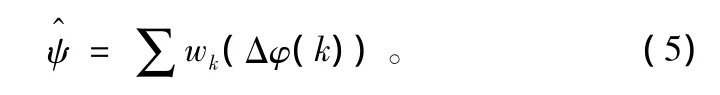
式中,wk为窗函数。ψ的估计值会随着窗函数的不同有较大差异,对于最简单的窗函数可得:
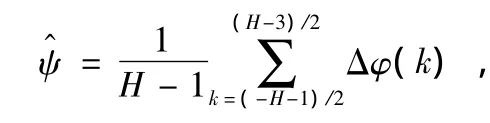
但通过这种方法得到的ψ不是最优估计值。文献[4]给出了ψ的无偏估计算法。观测矢量
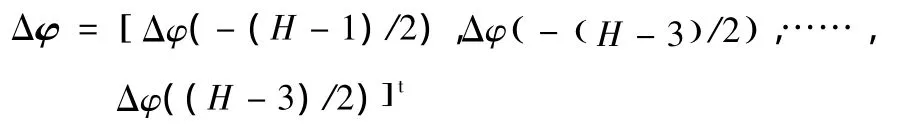
(t表示求转置)的条件概率密度函数为:
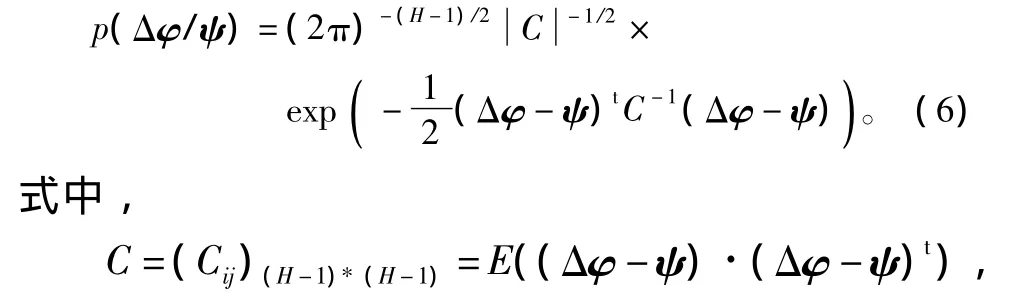
ψ=[ψ,ψ,……,ψ]t,为协方差矩阵。通过最大似然估计准则,得出ψ无偏估计的计算公式为:
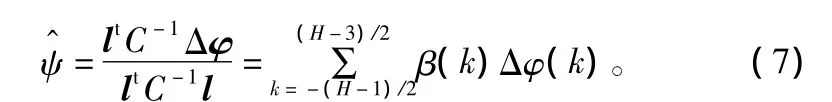
式中,l= [1111……1]t;β(k)为式(5)中的窗函数wk,且有
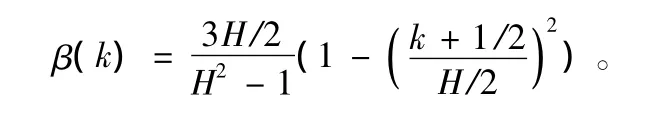
文献[5]已经证明式(8)中估计量的方差与有效估计的Cramer-Rao界一致:
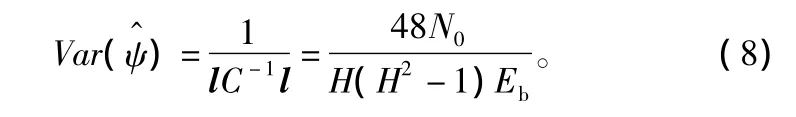
由上两式可得归一化载波频偏ΔfT的无偏估计和估计方差:
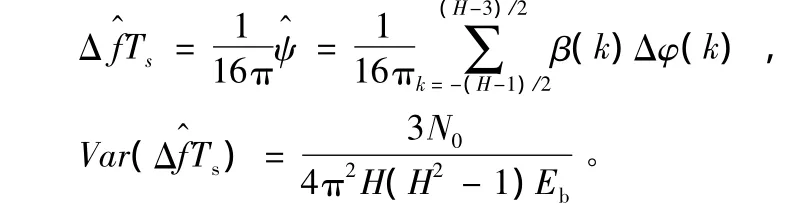
所采用的频偏估计器的仿真模型如图2所示。

图2 载波频偏估计
3 载波相位估计
由于突发中的 Δf和 θ0均需独立估计[6],所以先对输入复信号进行非线性操作,让抽样后的同相和正交分量(xn,yn)通过非线性变换得到复采样值):
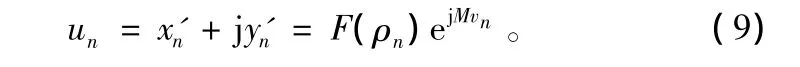
式中,ρn=;vn=arctan(yn/xn);F(·)是 ρn的非线性变换;F(ρ)=,且 m ∈{0,1,2,…,7}。
由un得到相位平均值,
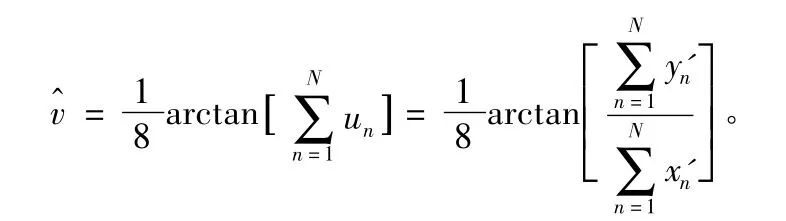
4 仿真结果及分析
在存在定时误差的情况下,定时同步后对不同信噪比情况下的频偏估计情况和相位预测情况进行仿真。载波频偏估计均值在不同信噪比条件下的曲线图如图3所示。
仿真条件:滚降系数α=0.35,符号数1008,4倍采样,归一化定时误差为 ±1/16,仿真次数1000次,为了避免归一化频偏与FFT的点数成倍数关系而造成的载波频偏不准确的问题,归一化频偏设为1/64+1/4096。
如图3所示,频偏估计均值在0.0159附近,与归一化频偏相符合。
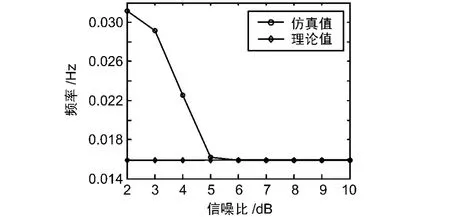
图3 频偏估计均值
在Eb/N0=5 dB和6 dB,数据长度1008,仿真次数104情况下采用上述频偏估计形式,估计载波频偏,验证估计精度。图4可以看出仿真次数为104的情况下,当Eb/N0=5 dB的时候,经统计有172个不满足解调要求的点,当Eb/N0=6 dB时,只出现了5个以内不满足要求的点,载波频偏满足估计精度要求。
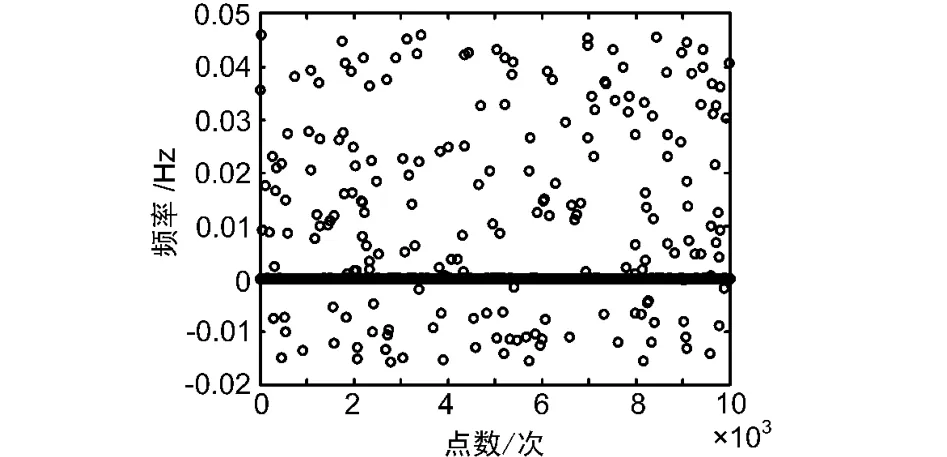
图4 Eb/N0=5 dB时的载波频偏估计精度
在频偏估计之后对本地载波的相位差进行估计,如图5所示。符号速率16 Hz,初始相差22.5°,相位估计器长度16,在不同信噪比下信号的相位差均值相对估计均值变化不大。载波初始相位差的估计值能在 -π/8~π/8变化,这是因为8PSK的相位是以π/4为间隔的。
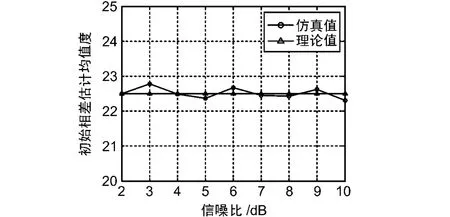
图5 相位差估计均值
因此可以得出相位估计法在实际解调过程中可以比较有效地消除载波相差,完成解调。由图6可以看出,解调器的比特误码率性能与理论值相比较仅下降了0.3 dB左右,和理论的误码率很接近,因此所提出的载波相位和载波频偏估计算法都是在较低信噪比条件下的性能也比较好。
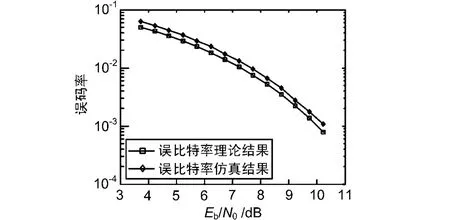
图6 算法解调误码性能
5 结束语
开环估计算法在解调过程中能避免“悬隔效应”的产生,可以有效地实现载波频差和相差的消除,实现信号的载波同步。该算法相对传统的科斯塔斯环可以对突发信号进行快速有效的解调,为以后突发TDMA解调的研究打下了良好的基础。
同时对载波恢复中相位估计算法的研究,为以后研制较高速率的数字化突发信号解调器提供了理论和实验依据。 ■
[1]VITERBI A J,VITERBI A M.Nonlinear Estimation of PSK Modulated Carrier Phase with Application to Burst Digital Transmission[J].IEEE Trans Inform,1983,29(4):543 -551.
[2]MORLET C,BOUCHERET M L.Low-complexity Carrier Phase Estimator Suited to on Board Implementation[J].IEEE Trans Inform,2000,48(9):1451 -1454.
[3]TRETTER S A.Estimating the Frequency of a Noisy Sinusoid by Linear Regression [J].IEEE Trans Inform,1985,31(6):832-835.
[4]POOI Y,PRANESH S.A Viterbi-Type Algorithm for Efficient Estimation of M-PSK Sequence over the Gaussian Channel with Unknown CarrierPhase[J].IEEE Trans Inform,1995,43(9):2429 -2433.
[5]KAY S.A Fast and Accurate Single Frequency Estimation[J].IEEE Trans Inform,1989,37(12):1987 -1990.
[6]LUISE M,REGGIANNINI R.Carrier Frequency Recovery in ALL-Digital Modems for Burst-Mode Transmissions[J].IEEE Trans Inform,1995,43(2/3/4):1169-1178.

