环形交叉口通行能力分析

张世亮，王小东

（长安大学 公路学院，陕西 西安 710064）

随着我国经济的发展，城市面积不断扩张，道路网建设也越来越密集，多条道路相交的情况越来越普遍，作为解决这种交通问题的有效手段之一，环形交叉口的广泛应用势在必行。但是在应用的过程当中也产生了许多的问题，由于环形交叉口的通行能力一般只有普通交叉口或者路段的一半，经常引起交通拥堵。研究环形交叉口的交通特性，改善其通行能力，对于我国未来发展具有实际意义。对于环形交叉口的通行能力的定义，在《道路通行能力分析》一书中给出：环形交叉口的通行能力为在一段时间段和通常道路，交通，管制条件下，并且假设在良好的气候条件和路面条件下，能合情合理地期望车辆通过车道或道路均匀断面的最大小时交通量。

1 我国环形交叉口概况

1.1 通行能力影响因素

影响环形交叉口通行能力的因素包括中心岛半径，进口渠化，交通组成，流向组成等。

1）由于中心岛的半径的限制作用，在环岛内形式的车辆的车速不可能很高，在微型环形交叉口，由于受半径的影响，需要连续的转弯来改变方向，转角过大，为了有更大的扭矩，车速会大幅降低，影响到环形交叉口通行能力。

2）环形交叉口的实质是对道路的渠化，这样就明确了道路上各个方向的路权，对于冲突的减少和提高通行能力都有重要的意义。

3）环形交叉口的临界间隙和随车时距受到车辆类型的影响。在大型车比例较高的交叉口内，由于自身的性能原因，必然产生速差。为了保持安全状态，需要更大的行车间距，这就减小了通行能力，同理，对于随车时距也有较大的影响。

4）环形交叉口在进入时避免冲突的发生，但是在出环岛时却产生冲突点，不同流向的交通流在交叉口里的行驶距离不同，其受影响程度也不相同，即左转车辆的比例越大，通行能力越低。

其中，临界间隙是指交叉口允许次要道路某等待穿越车辆通过主要道路所需的最短时间。随车时距是指支路排队车辆连续通过交叉口时相邻两车之间的时间间隔。

1.2 环形交叉口交通特性

1）交叉口渠化：交叉口内一般渠化较好，增加了行人和非机动车流，所以一般要设置人行道，有的还设置了专门的非机动车道及机非隔离设施。

2）空间利用较好：由于城市用地限制，环形交叉口形成的巨大环岛成为新的开发热点。可以在环岛上设置一些有象征意义的雕塑，建筑或广场，充分利用土地。

3）公交车站点的设置：由于在环形交叉口的出口道上设置了公交站点影响了进入交叉口交通流连续性，吸引了大量的行人，干扰了交叉口通行。

2 环形交叉口通行能力计算方法

环岛形交叉口的特殊结构和交通流的特性，在分析它的通行能力时需要对于进口车道条数的不同情况区别分析，分析的原理主要基于间隙接受理论模型，同时也有一些经验方法，在此只就间隙接受模型做简要研究。

2.1 单环道交叉口

2.1.1 一般理论方法

当进车道为一条车道时，这样的环形交叉口的间隙接受模型可从两股车流相互作用时的排队模型中推导出来。由于在这样的环形交叉口上无法进行超车行为，可以认为车头时距服从移位负指数分布，在交通较为拥堵，可自由行驶的条件下，认为车流会以最小行车时距tm（s）行驶，假设ɑ表示车头时距大于tm（s）的自由流比例，环形车流量为q（pcu／s），环形车流的车头时距大于和等于tm（s）概率分别为ɑ和1－ɑ，同时设tf为进环车流的随车时距，即当环形车流的车头时距较大时，允许两辆车以上进入时，进口车道上排队进入环形交叉口时的相邻两车的车头时距。

当tc＜h＜tc＋tf时，允许一辆汽车进入交叉口；当tc＋（1－k）tf＜h＜tc＋tf时，允许k辆车进入交叉口。设环形交叉口车流出现tc＋（1－k）tf＜h＜tc＋tf的概率为

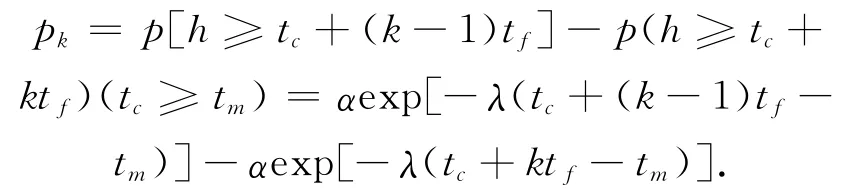
设进环车辆的通行能力为ce，则

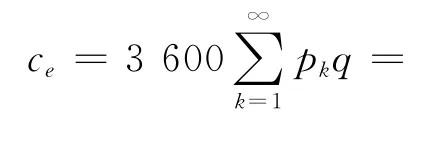
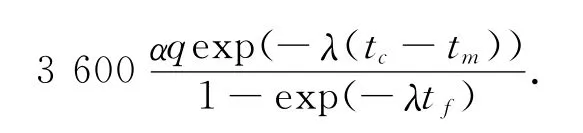
2.1.2 改善方法

对于移位负指数方法还可以进行改进，用M3分布假设车流由两部分组成的，一部分以车队状态行驶，另一部分按自由流状态行驶。其余假设同上述一致

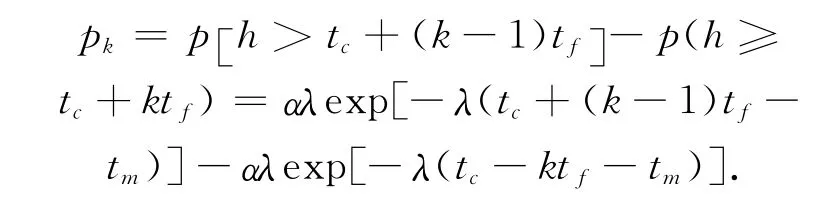
式中：tm（s）为最小车头时距，λ为衰减常量，α为自由车流的概率。

这几个参数之间的关系有

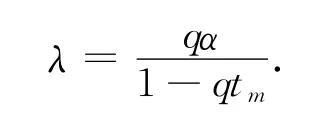
设进环车辆的通行能力为ce，则

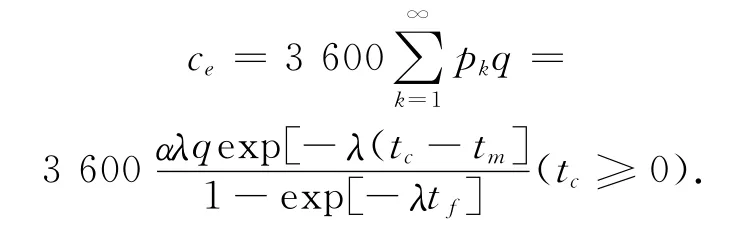
这种方法只需要tc≥0就可以应用，更为普遍。上面所述的方法是较为理想化，在实际的情况中达不到使用条件，为简化计算，在公路通行能力手册中给出较为简便的计算方法。

2.1.3 实际使用方法

对于进口道为一条的环形交叉口，其冲突方式体现为环形车道交通流与进口道交通流的交叉运行，单环行车道有明显的优先性。单车道环形交叉口的优先等级为，沿中心岛运行的交通流处于较高的优先等级，而希望进入环形交叉口的车辆则处于较低的优先等级。结合冲突流的理论得出各个进口道冲突交通量计算方式（见表1）。

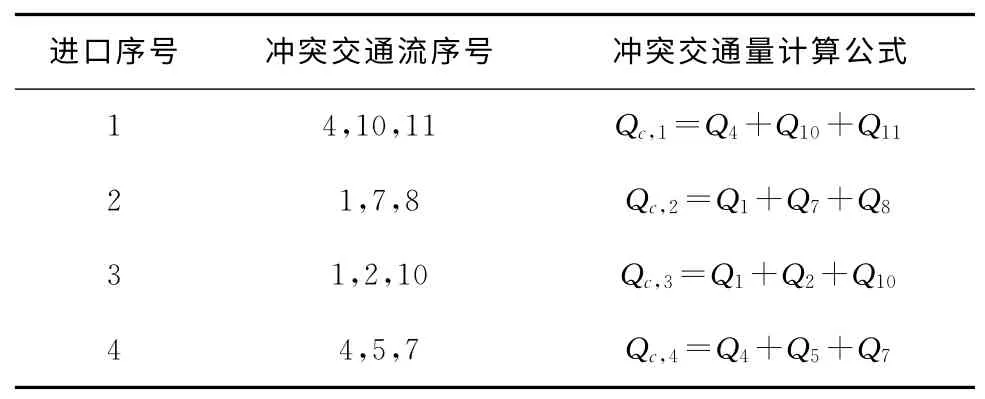
表1 一条进口道环形交叉口冲突交通量计算方法

临界间隙指车流中出现的最小可接受间隙，这个间隙往往无法观测，但是对于随车时距已通过大量的实测数据得出，而这两个参数之间存在着一定的关系，这给标定参数带来方便。一般随车时距与临界间隙比在0.5～0.6。在公路通行能力手册中给出以下参考数据（见表2），供实践时参考。

表2 一条进口道环形交叉口临界间隙和随车时距

由以上表格，结合冲突流理论模型可以得出基于此理论的单环道交叉口通行能力计算公式

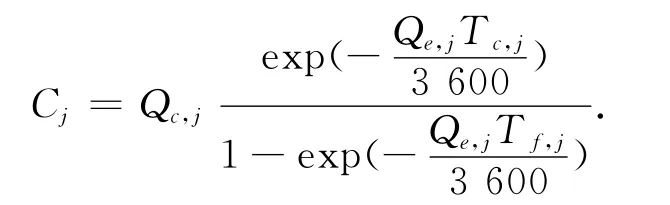
式中：cj为进口道的通行能力，pcu／h；Qc，j为进口j的冲突交通量，pcu／h；Tc，j为进口j中车辆进入环行车流时需要的临界间隙，s；Tf，j为进口j中的随车时距，s。

2.2 双环道交叉口

2.2.1 一般方法

当进口道和环形交叉口车道均为两条，车辆进入交叉口时，左侧车流与外侧环形车流穿插并与内侧环形车流合流，而右侧车流只与外侧环形车流合流。设ce1和ce2分别为左，右两侧进口车道能够进入交叉口的车辆数，计算方法如下所示，ce2的计算方法与进环车道为一条时的计算方法相同

ce＝ce1＋ce2.

当左侧车辆进入交叉口时，可把环形车流假设成一当量车流与原车流具有以下对应关系：

1）当量车头时距大于tm时，服从移位负指数分布；当量车头时距小于tm时服从均匀分布。

2）当量交通量等于两车道交通量之和，即q＝q1＋q2，式中q1，q2分别为内，外侧环形车流的流量。

3）当量车流车头时距小于tm的概率为p（t＜其中为两环形车流平均车头时距的均值，即基于以上假设，可推出当量车头时距具有的分布形式

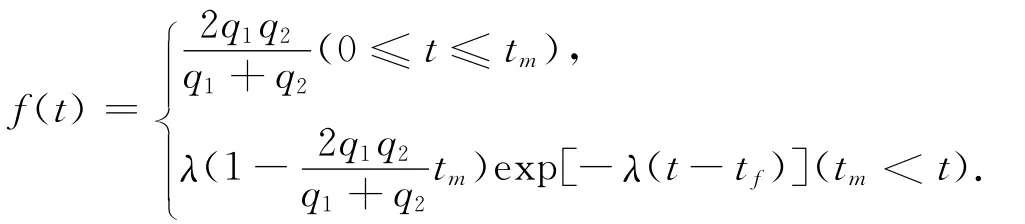
式中

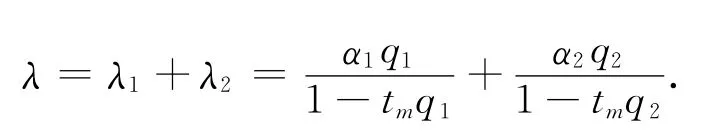
左侧车道的通行能力公式如下

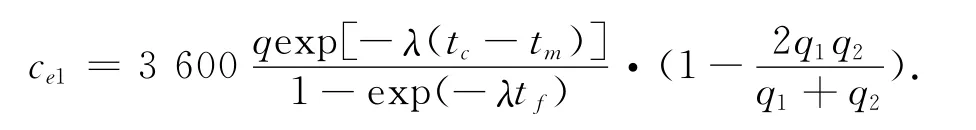
进环车道总通行能力公式如下

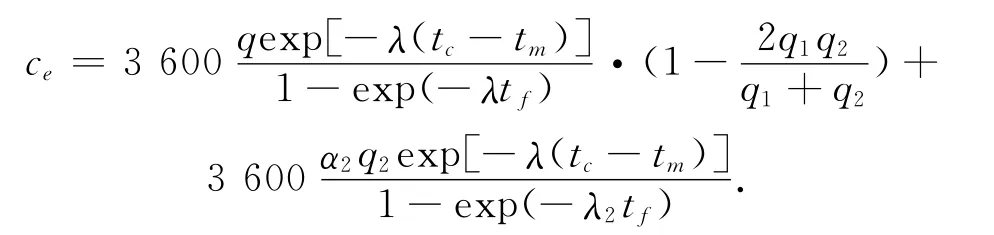
2.2.2 改善方法

类似的，也可以用M3分布对上述方法进行修改，修改后的M3分布对于描述公路上的车辆状况更为客观

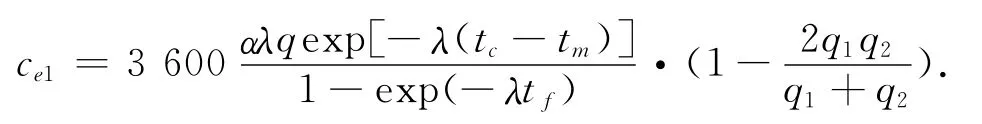
总通行能力

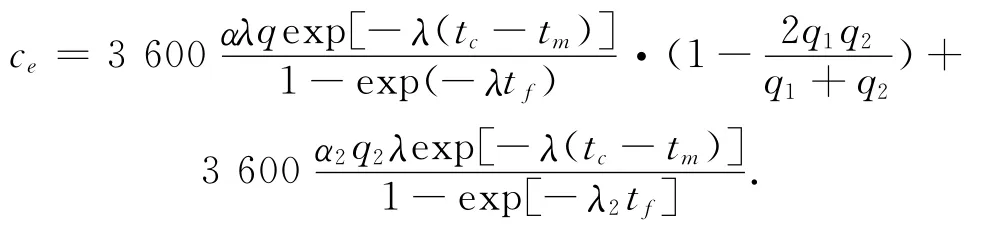
2.2.3 实际使用方法

两个进口车道的环形交叉口采用冲突模型来分析，冲突交通量指与进口左转和直行交通量与对向左转以及左侧进口的直行交通量之和，计算方法见表3，冲突示意图见图1。为简化计算，将双环行车道的环形交叉口运行规律简化。其中：

1）环形交叉口两个环形车道的出环车流成为出环车流A。

2）环形交叉口环行车道的所有绕环行驶的车流成为绕环车流D。

3）环形交叉口入口处两个车道中的右转车流C。

4）环形交叉口入口处来那个车道中入环车流成为环车流B。

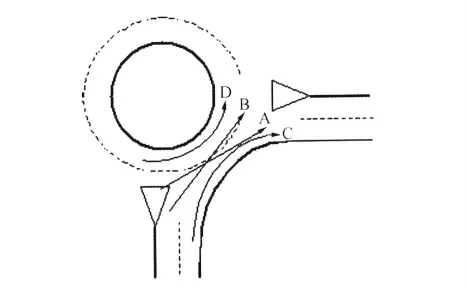
图1 双环道交叉口交通特性

表3 双环道交叉口交通流计算公式

同样，根据冲突流理论模型可以给出相应的双环道交叉口通行能力计算公式

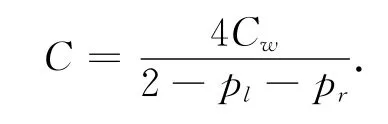
式中：C为交叉口通行能力，pcu／h；pl为各进口的左转车比例之和；Cw为交叉口中交织区通行能力，通常取1 700pcu／h；pl为各进口的左转车比例之和。

这样的方法不论在形式上还是在思路上都与理论相去甚远，为了能够应用理论方法，下面对照单环道通行能力（见表4），给出相应的通行能力计算公式

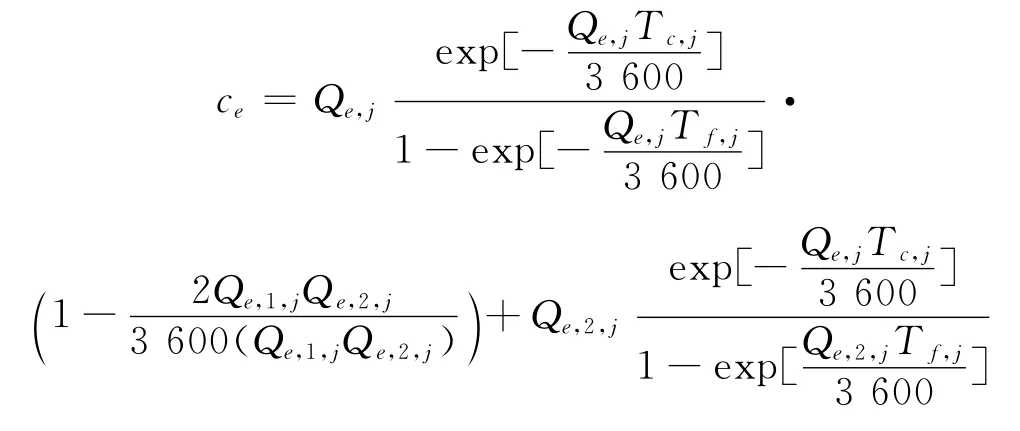
式中：ce为双环道通行能力；Qe，j为进口道j的冲突交通量，其值为Qe，1，j和Qe，2，j的和；Tc，j为进口j中车辆进入环行车流时需要的临界间隙，s；Tf，j为进口j中的随车时距，s。

表4 改进方法的双环交叉口交通流计算公式

3 环形交叉口的评价

3.1 延误

3.1.1 延误的一般方法

延误分为几何延误和交通延误。前者由交叉口几何形状确定。包括车辆加减速和转弯引起的延误。不同类型交叉口，几何延误不同。具体如表5所示。

表5 不同尺寸环形交叉口几何延误

在分析交通延误时，由于与交通流的大小即排队的长度有关，根据饱和度区别分析：在饱和度小于1，即交通流较为稳定，观测时间满足下式时，所计算的交通延误可信度较高

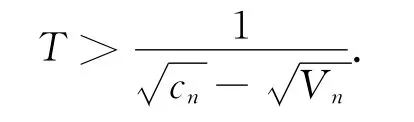
式中：cn为环形交叉口通行能力，pcu／h；Vn为进口车道上交通流率，pcu／h。

交通延误模型为

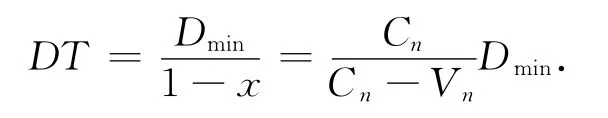
式中：x为进环车流的饱和度（CV／Cn），其中CV为进口道上的车流量；Dmin为延误时间，s，无信号控制交叉口优先型交通流延误。

如果进入环岛的车流排队长度为几何分布时，则

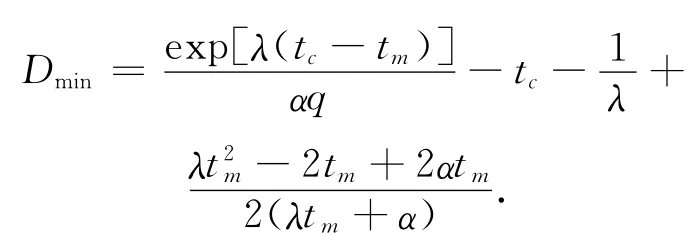
由于进环车辆随时间不停的变化，车辆延误在一段时间内不稳定，为了能够应用上式计算，将区间划分成几段，假定在不同段内，车流稳定，进行加权计算得下式

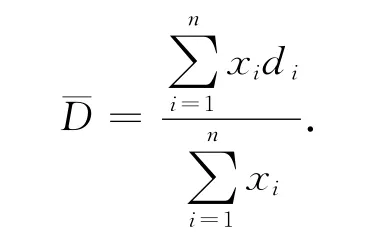
式中：di为第i个时间间隔内延误，xi为第i个时间间隔内的饱和度，n为时间间隔数。

3.1.2 延误的改善方法

对于不稳定状态的交通流，引入微积分概念，将计算区间划分成n段，用环道上交通量做为自变量，这样得出的数据跟加精确，得出的曲线也较为平滑。用积分中值定理类似的有计算公式为

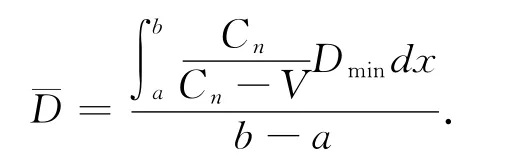
其中V表示进环车流的交通量。所以，环形交叉口的总延误时间为

D＝DT＋DG.

对于环形交叉口的通行能力评价，通常采用无信号交叉口的服务水平进行划分。道路服务水平是指道路使用者从道路状况，交通条件，道路环境等方面可能得到的服务程度或服务质量（见表6）。

表6 适用于我国的公路无信号交叉口服务水平的划分

4 结束语

本文在已有成果基础上，对现存的环形交叉口通行能力计算做了部分改进。旨在为后续的研究提供一定的参考，同时，存在着不足，只是就基本通行能力的计算上进行讨论，但是由于地域差异的存在，实际中还需要对基本通行能力进行折算才能够应用到实践中去。

［1］陈宽民，严宝杰.道路通行能力分析［M］.北京：人民交通出版社，2003.

［2］周荣贵，荣建，任福田，等.公路通行能力手册［M］.北京：交通部公路科学研究院，2006.

［3］郭采香.城市无信号环形交叉口通行能力及延误研究［A］.江苏：东南大学出版社.2008.

［4］徐吉谦.交通工程总论［M］.北京：人民交通出版社，1993.

［5］王炜，过秀成.交通工程学［M］.江苏：东南大学出版社，2000.

［6］李正元.高等数学辅导［M］.北京：国家行政学院出版社，2004.

［7］张生瑞.交通流理论与方法［M］.北京：中国铁道出版社，2010.

［8］王正武，张亚萍.无信号交叉口次要道路通行能力［J］.中南公路工程，2001（2）：70－71.

［9］李芳，吴芳.基于交通冲突技术的交叉口安全评价［J］.交通科技与经济，2011（5）：64－66.