预应力混凝土箱涵结构理论分析及计算

颜 毅，肖 伟，马占武

（1.林同棪（重庆）国际工程技术有限公司，重庆 401121；2.重庆市建筑科学研究院，重庆 400015）

我国设计的箱涵最常用的跨径一般为1～4m，跨径5m 以上的箱涵很少设计。随着高等级公路的快速建设发展，桥梁设计中经常设置成单孔小跨径，如果基础承载力不能满足要求，通常的做法是增大跨径、加设桥孔数量或把桥台设置成桩基础，势必成倍提高工程难度及价格。箱涵有其独特的优势，对地基承载力的要求较低、具有较好整体性且受力合理，如果施加预应力，则箱涵的孔径可以进一步增大。对于不符合要求的地质，尽量把桥改为涵，就能大大降低工程造价。相对于普通钢筋混凝土箱涵，施加预应力可以减小箱涵顶、底板的厚度，节省混凝土用量，防止混凝土开裂，增加箱涵的耐久性、降低成本、延长使用寿命。

1 箱涵预应力筋形状及布置方法

预应力筋布置及外形应尽可能与弯矩图一致。当承受均布荷载时，用正反抛物线形式；当承受集中荷载时，预应力筋在集中力处弯折，按折线形布置，折线形布置方案不宜用于三跨以上的箱涵，施工困难，预应力损失较大；侧墙端部弯矩较小的单跨或多跨预应力箱涵，顶、底板外端采用直线与抛物线相切的布筋方式，可减少预应力损失；通过箱涵板和墙交界处的预应力筋，应尽量使核心区混凝土均匀受压，采用正反抛物线与直线的混合布置方式；顶、底厚度较小的箱涵，当满足设计要求时，采用直线预应力筋，施工方便，预应力损失小；多跨箱涵布筋可采用上述形式进行组合；必要时可在侧墙设置预应力，当侧墙较厚时采用侧抛物线与直线混合布置的形式，当墙体较薄时采用直线预应力。

2 箱涵预应力筋线形公式

箱涵顶、底板预应力筋的布置，应使预应力筋的外形尽可能与外力作用下顶、底板的弯矩图形一致，对于板端弯矩与板跨中弯矩基本相近的单孔箱涵，预应力筋布置成正、反抛物线是一种被广泛采用的形式，如图1 所示。正、反抛物线在反弯点C（或E）处相切，且C（或E）点位于B（F）与D的抛物线上，其抛物线方程为

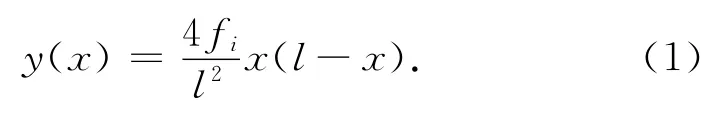
式中：fi和l分别为抛物线的矢高和跨度；图1 中f1和f2为BC（EF）段和CE段抛物线矢高。

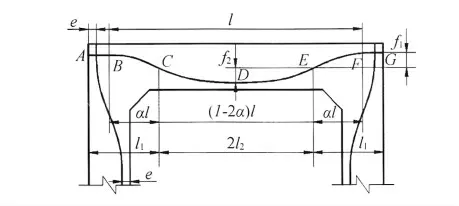
图1 箱涵预应力钢筋线形

f根据预应力筋的排列而定，宜取最大值。

连接BD，根据得到的两个直角三角形对应边成比例的关系，得

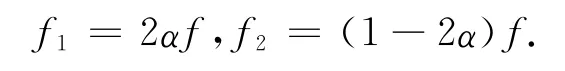
将f1和f2代入式（1）得板端BC（或EF）段抛物线方程为

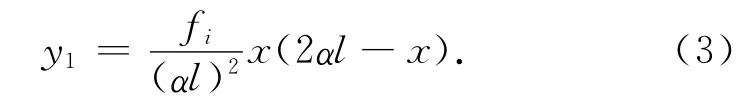
跨中CE段抛物线方程为

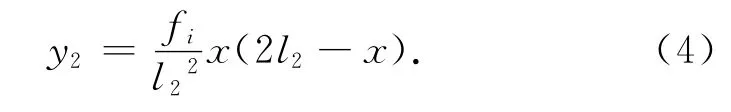
α在0.1～0.2取值为宜，其他预应力筋的布置形式类似。

当箱涵侧墙预应力筋的布置形式尽量接近荷载弯矩图形，在侧墙顶、中截面偏心距e应取最大值，如图1所示。对于板端弯矩较小的单孔或多孔箱涵的侧墙，侧墙预应力筋布置成直线与抛物线相切的形式。

3 箱涵顶、底板正截面承载力计算

预应力箱涵顶、底板承载力计算公式，预应力筋有效预应力为σpe，预应力以等效荷载的形式作用于结构，箱涵板弯矩为Mp、轴力为Np，孔道灌浆后，由变形协调原理，在极限荷载时应力增大至极限强度fpy，预应力筋的应力增量为fpy－σpe。设外荷载作用下控制截面的弯矩设计值为Ms，等效荷载作用下的弯矩值为Mp，轴力Np（压力为正），设预应力荷载分项系数为1.0，取控制截面隔离体，如图2所示，由平衡方程∑M＝0及∑X＝0得

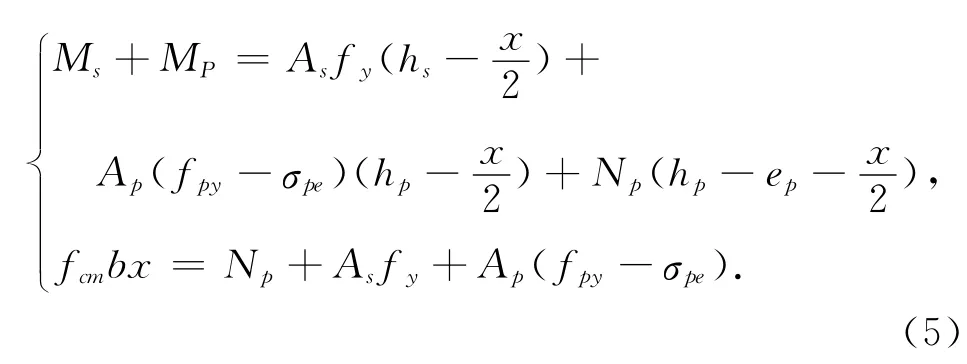
式中：ep为预应力筋合力点距截面形心轴的距离，Ap为预应力筋面积，As为非预应力筋面积，hp为预应力筋形心至混凝土受压边缘距离，hs为非预应力筋形心至混土受压边缘距离。

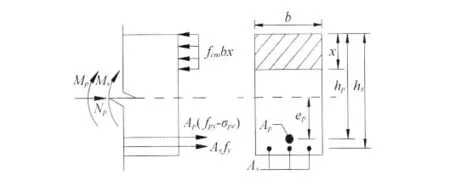
图2 控制截面隔离体

Np与Apσpe关系，对于轴向无约束的梁板，二者相等；对轴向有约束的梁板，Np小于Apσpe。如果侧墙抗侧刚度较大，则顶、底板均张拉预应力，否则侧墙将发生顶、底板的轴向变形，阻止预应力向顶、底板中传递，产生次拉力，其值为Np－Apσpe，降低顶、底板的承载力。

4 箱涵承压计算

4.1 端部承压的截面尺寸计算

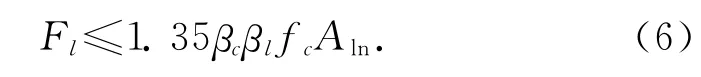
式中：Fl为混凝土的局部承压的预应力，Fl＋1.2σcon Ap；fc为混凝土的轴心抗压强度，在后张法预应力混凝土构件的张拉阶段的验算中，应根据相应阶段的混凝土立方体抗压强度值以线性内插法确定；βc为混凝土强度影响系数；βl为混凝土局部承压时的强度提高系数；Ab为局部承压状态下计算底面积；Al为混凝土局部承压状态面积；Aln为混凝土局部受压状态净面积。

4.2 局部承压承载力验算

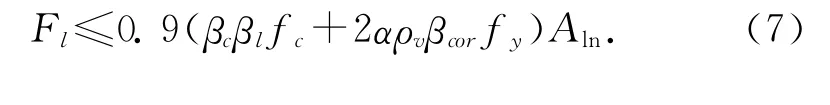
当间接钢筋为方格时

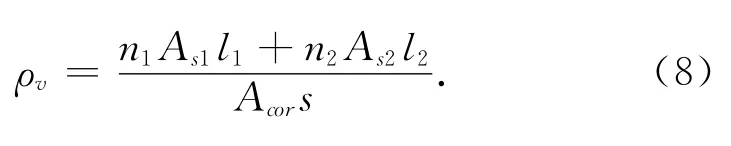
当间接钢筋为螺旋筋时

式中：βcor为局部承压强度的提高系数；ρv为间接钢筋的配筋率；α为间接钢筋约束作用的折减系数；n1，As1为钢筋网在梁截面宽度的根数及单根钢筋截面积；n2，As2为钢筋网在梁截面高度的根数及单根钢筋截面积；As3为螺旋钢筋截面积；dcor为螺旋式间接钢筋内表面的截面面积；s为钢筋间距。

5 箱涵挠度验算

5.1 刚度计算

受弯构件的刚度B可按下式计算为

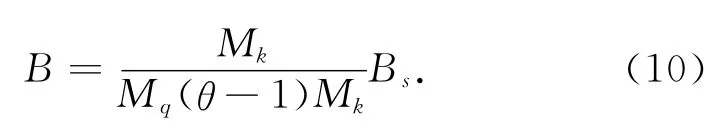
式中：Mk为按荷载效应的标准组合计算的弯矩取计算区段内的最大弯矩值，Mq为按荷载效应的准永久组合计算的弯矩取计算区段内的最大弯矩值，Bs为荷载效应的标准组合作用下受弯构件的短期刚度，θ考虑荷载长期作用对挠度增大的影响系数。

5.2 挠度验算

短期荷载作用下挠度和预应力引起的反拱值，由弯矩图形相乘法，得梁板挠度为

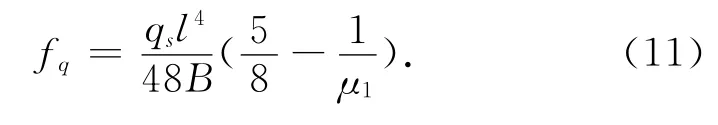
预应力引起的梁板反拱值为

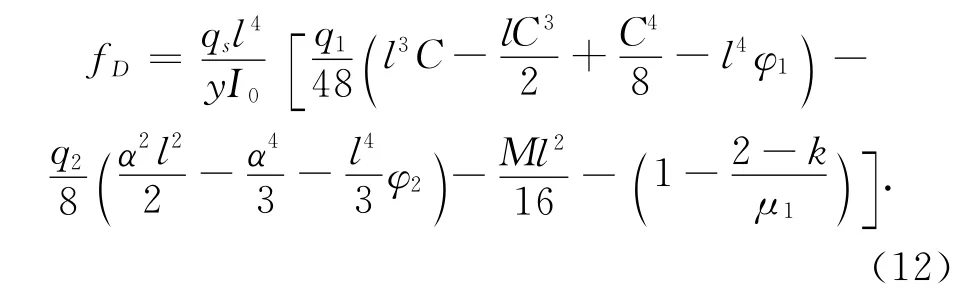
式中：k为箱涵顶、底板与边侧墙的线刚度之比；

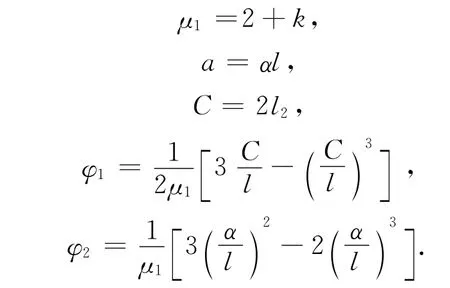
式中：a为预应力筋的回缩量。

挠度验算为

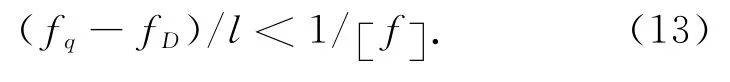
6 箱涵结构设计

6.1 工程实例

计算荷载：公路Ⅰ级；净跨径：l0＝8.6m ；净高h0＝8.8m；填土厚度：H＝8m；材料：砼C30，主钢HRB335；材料容重：填土r1＝19kN／m3；钢筋砼r2＝26kN／m3；土的内摩擦角φ＝30°；基底置于卵石土上，［σ］＝400kPa。

6.2 预应力箱涵结构设计

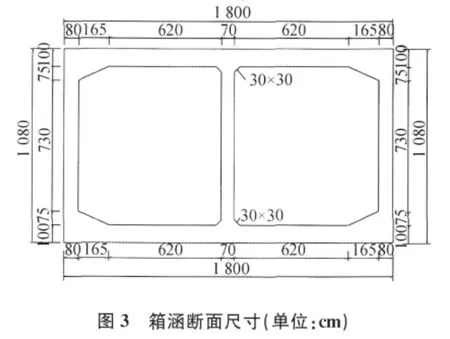
原设计为混凝土箱涵，其截面尺寸如图3所示。现对箱涵的顶、底板施加预应力，计算所用尺寸参数与原箱涵相同，两种曲线预应力布置方式及MIDAS有限元计算模型如图4 所示。其中，（a）种布束方式的钢束末端偏离顶、底板中心进行锚固定，（b）种布束方式在顶、底板的中心进行锚固定。

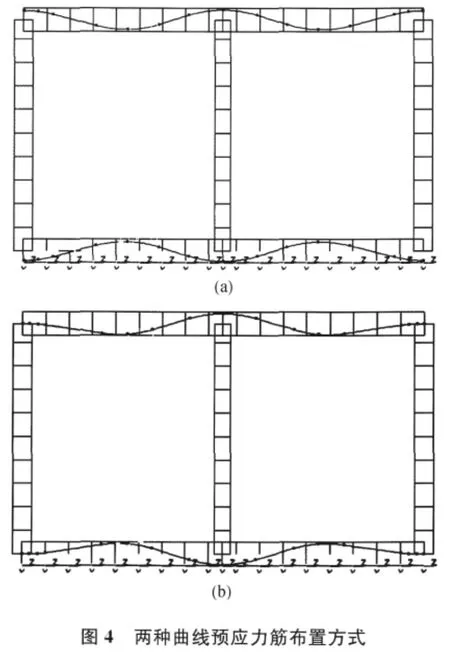
计算结果表明，在布置相同数量预应力筋的情况下，短期及长期效应组合下的应力，两种布束方式应力相差不大，箱涵顶、底板混凝土单元没有拉应力出现，均为压应力，（b）种布束方式较好，且施工更方便。

为达到与原设计相同的效果，并体现出预应力在合适截面下的优势，在保持混凝土箱涵其他尺寸不变的情况下，仅把顶、底板厚度减为30cm 进行计算（原箱涵顶、底板厚100cm），采用直线预应力钢束，计算采用单位宽度计算时，顶、底板分别用了8根φ15.2的预应力钢筋，预应力布置和计算模型如图5所示。

计算结果表明，在短、长期效应组合下，箱涵的顶、底没有拉应力的出现，不会有裂缝的产生，混凝土的耐久性得到了保证。与原设计相比，顶、底板可节约混凝土70%，其配筋仅为构造配筋。

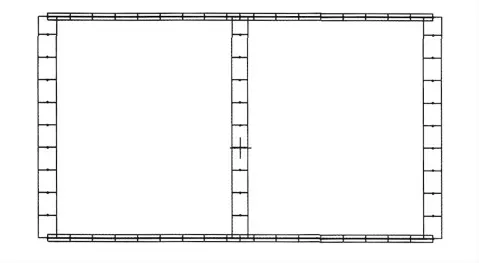
图5 直线预应力筋布置方式

7 结束语

通过对预应力混凝土箱涵的理论分析，得出了预应力筋的几种布置形式、布置方法及计算公式。并对预应力混凝土箱涵的顶、底板正截面承载力、预应力荷载的分项系数、端部承压的截面尺寸、局部承压承载力进行理论分析，给出挠度验算公式及方法。最后，对预应力混凝土箱涵进行对比设计计算，结果表明，构件没有拉应力的出现，因此不会有裂缝的产生，混凝土耐久性有保证。采用单位宽度计算比较，顶、底板分别用8 根φ15.2 的预应力钢筋，与原设计相比，顶、底板可节约混凝土约70%，其配筋仅为构造配筋，可明显降低成本。

［1］熊学玉.预应力混凝土结构荷载效应组合及正截面承载力设计计算的建议［J］.工业建筑，1998（2）：1－5.

［2］GB5001022002混凝土结构设计规范［S］.北京：中国建筑工业出版社，2002.

［3］中华人民共和国交通部标准.JTG D60－2004 公路桥涵通用设计规范［S］.北京：人民交通出版社，2004.

［4］中华人民共和国交通部标准.JTG D62－2004 公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京：人民交通出版社，2004.

［5］聂利英，吴鸿庆.钢筋混凝土地道桥力学特性的研究［J］.兰州铁道学院学报，2001，20（3）：19－24.

［6］周家新.下穿铁路斜交框架桥的空间结构分析［J］.铁道建筑，2005（7）：31－33.

［7］陈锐，朱尔玉.施加预应力对框架式混凝土地道桥的影响［J］.铁道建筑，2007（11）：16－17.

［8］李家稳，张海燕.四孔连续框构桥设计技术的研究［J］.北京交通大学学报，2008，32（1）：12－19.

［9］张桃，肖盛燮，陶韬.预应力混凝土连接刚构桥预拱度的设置与控制［J］.交通科技与经济，2012，14（4）：7－10.