Stokes漂流对海洋上层混合层的影响研究＊

王智峰，吴克俭，2＊＊

（中国海洋大学1.海洋环境学院；2.物理海洋教育部重点实验室，山东 青岛266100）

Stokes［1］最早提出Stokes漂流的概念，认为表面重力波的非线性作用，导致海表水质点轨迹不封闭，使得它在波浪传播方向上，产生1个拉格朗日净输运，称之为Stokes漂流。Langmuir［2］提出“Langmuir环流”的概念，认为“Langmuir环流”是1种发生在上层海洋中，轴向平行风向的纵向螺旋状运动，是波流相互作用主要表现形式之一。Craik ＆ Leibovich［3－4］（即著名的CL理论）指出Stokes漂流与风驱水平流的相互作用，是引起“Langmuir环流”的核心机制，它们之间的相互作用力，us×ω（us为Stokes drift，f×u为涡度矢量），称之为“Stokes－Vortex力”。Skyllingstad ＆ Denbo［5］通过大涡模拟 （Large－eddy simulation，LED），对比发现加入“Stokes－Vortex力”后，海洋上层混合程度明显加强。McWilliams［6］在 CL 理论的基础上，提出了“Langmuir湍流”的理论。他认为上层湍流除了需要考虑传统的雷诺效应外，还需要考虑由Langmuir环流导致的湍动能增加项，它与Stokes漂流有关，称之为“Stokes湍动能生成项”。McWilliams et al.［7］在此基础上，建立了一个浅水模型，系统阐述了考虑“Stokes－Vortex力”后，近岸浪流之间的相互作用，以及由此引起的波浪增水、水位和压强变化等一系列物理现象。Li et al.［8］将“Stokes湍动能生成项”应用到 Mellor－Yamada 2.5层湍闭合模型中，同时考虑波浪破碎和Stokes漂流。模拟结果表明，波浪破碎效应主要集中在海表，而Stokes漂流引起的混合效应可以达到整个混合层。Uchiyama et al.［9－10］以 McWilliams et al.［7］理论为基础，先后建立了近岸正压和三维浪流相互作用模型，再次肯定了“Stokes－Vortex力”对加深混合等方面的作用。Kenyon［11］将海表面Stokes漂流速度与风速建立相关，认为Stokes漂流速度是随着风速大小变化的，同时Stokes输运可能会对海表面总的平均流产生重大影响。Hasselmann［12］提出，Stokes漂流与大尺度行星涡度的作用可以产生一项欧拉动量平衡下的力，f×us（其中f 为科氏参数），称之为“Coriolis－Stokes力”。McWilliams ＆ Restrepo［13］对Boussinesq运动方程和连续方程进行波浪平均，考虑“Coriolis－Stokes力”，提出了比较完整的大尺度波浪驱动的大洋环流理论框架，从流体输运角度指出了波浪诱导的输运在高风速区可达与风生环流输运可比较的量级。Wu et al.［14－15］考虑“Coriolis－Stokes力”，给出常涡粘性系数下波浪对Ekman层能量输入的解析表达式。研究指出，海洋Ekman层的机械能输入包括两部分：一是风应力对Ekman层的直接能量输入，其受波浪的影响；二是波浪对Ekman层的能量输入，其与风应力、波浪参数和波向与风应力的相对方向有关。Deng et al.［16］利用POM－SWAN耦合模式进行理想实验，对“Coriolis－Stokes力”驱动的流速和导致的能量输入变化进行研究，揭示了“Coriolis－Stokes力”对海洋上层环流影响的重要性。

由此可见，在海洋上层混合层中Stokes漂流是“Stokes－Vortex力”和“Coriolis－Stokes力”的重要源项，起着举足轻重的作用。然而，以前的研究是将小尺度的“Stokes－Vortex力”和大尺度的“Coriolis－Stokes力”分开来研究。而且在研究的过程中，多采用单独的湍流模型来研究“Stokes－Vortex力”，或采用单独的动量模型来研究“Coriolis－Stokes力”，而没有将动量、温盐、湍流等效应综合在一起进行研究。本文的目的是将两种力结合起来，着眼于大、中尺度，在计算中既考虑“Stokes－Vortex力”引起的湍流混合效应，又考虑了“Coriolis－Stokes力”对流速剖面的改变和对温盐等的输运作用，以此来综合研究Stokes漂流对海洋上层混合层的影响。

2 数值模型

2.1 波浪平均的N－S方程

对于粘性不可压缩流体，动量方程和连续方程可以写为

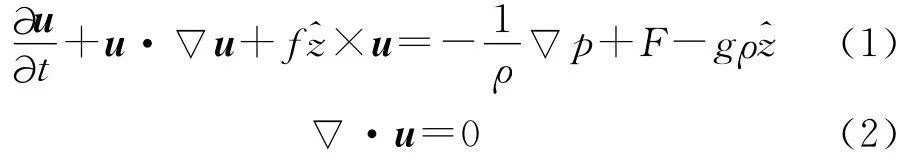
对珔u进行时间平均

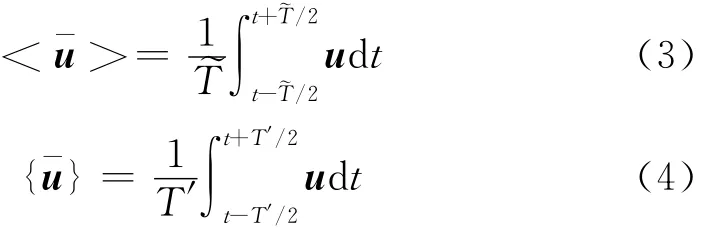
其中：＜u＞表示波浪尺度平均；｛u｝表示湍扰动平均，有

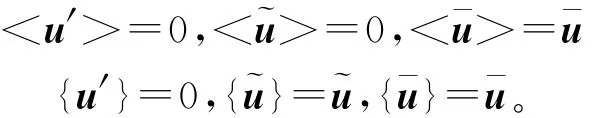
这样，将u＝珔u＋珘u＋u′，p＝珚p＋珟p＋p′代入方程（1）和（2），进行时间平均，可以得到

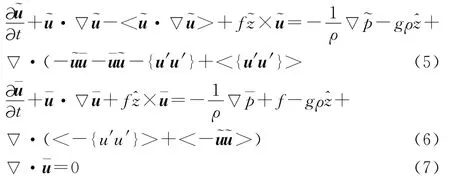
其中：（5）为波动方程，（6）为平均动量方程。

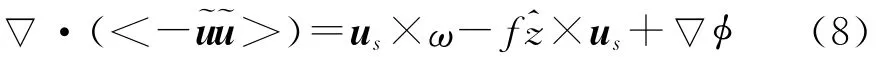
其中：us为Stokes输运速度，若为线性单频波，表达式为

us×ω（ω 为涡度矢量），称之为“Stokes－Vortex力”，是 1 种 小尺 度 力。Craik ＆ Leibovich［3－4］指 出Stokes漂流与风驱水平流的相互作用力，us×ω，是引起Langmuir环流的核心机制。

f＾z×us，称之为“Coriolis－Stokes力”，是1种大尺度力。许多学者［12，17－19］认为，考虑地球旋转后，垂直波浪传导方向产生偏移，会诱导产生1个波浪应力项，即是“Coriolis－Stokes力”。

McWilliams et al.［7］和 Lane et al.［21］对温盐方程进行波浪平均，得到

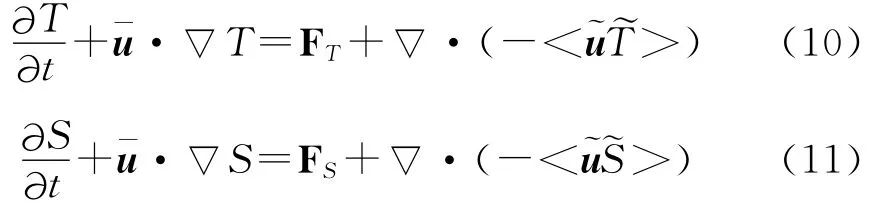
其中：

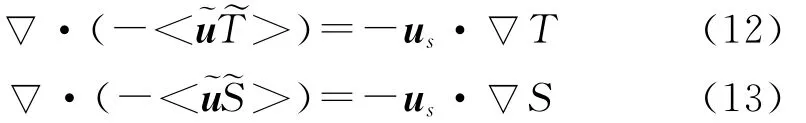
即波浪扰动和温盐扰动的相互作用项，可以表达为Stokes漂流对温盐的输运。

McWilliams［6］以 Langmuir数 作 为 衡 量 “Langmuir湍流”和雷诺效应相对大小的标准，Langmuir数越小，表明该海区“Langmuir湍流”越占主导。Sullivan，et al.［22－23］在 McWilliams［6］的理论上进行发展和完善，形成如下的湍动能方程：

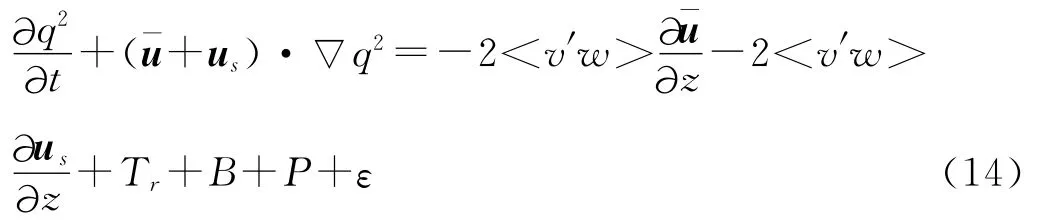
2.2 POM模式的应用

POM 模式（Princeton Ocean Model）是由美国普林斯顿（Princeton）大学Blumberg和 Mellor于1977年共同建立起来的1个三维斜压原始方程数值海洋模式，经过不断的改进，成为国内外应用较为广泛的河口、近岸海洋模式。将上面的数值模型应用到POM模式中，可以得到

连续方程：

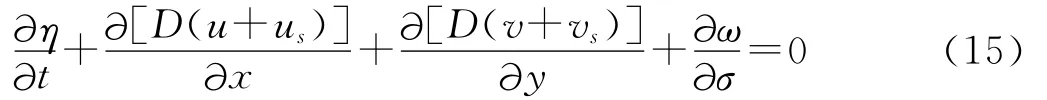
此处，

下面的研究主要基于修改后的POM模式进行数值计算。

2.3 实验参数的选取

若只考虑温度和压强对密度的影响，有

其中：u＊为海面摩擦速度；σs为Stokes漂流影响深度；n1，n2为系数；n1表示特征速度与u＊之比；n2表示特征尺度与δs之比。

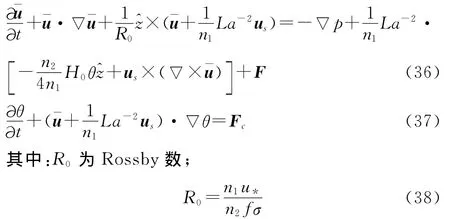
H0为 Hoenikker数，Skyllingstad ＆ Denbo［5］用它来衡量某一过程中，输入输入热量的相对变化；

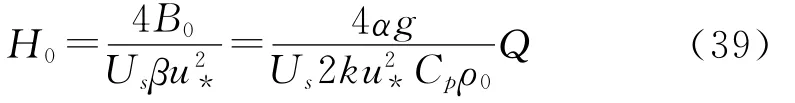
La为Langmuir数，表示海面摩擦速度与Stokes漂流的相对大小，Langmuir数越小，表示Stokes漂流越占优势。McWilliams［6］定义Langmuir数为

在本文的理想实验中，主要根据这几个参数的变化进行设计和计算研究。

3 数值实验

本文旨在研究Stokes漂流对上层混合层的影响，因为全球大部分海域的Stokes影响深度σs＝1／2k在20m以内，所以取恒定水深为20m的矩形网格进行数值实验。此外，不同风速情况下，Stokes漂流的大小会有变化，但是各变量随Stokes漂流的变化规律是相同的。经计算ECMWF再分析风场全球平均风速在7m／s左右，本文取恒定风速7m／s，方向自西向东。南北向取201个格点，东西向取101个格点，垂向分层为21层。取初始温度20℃，初始盐度30，科氏参数取中纬度特征值0.000 1。

3.1 空间尺度的变化

为了比较不同尺度下Stokes漂流的影响，选取了3种空间间隔进行研究，分别为180，1 800m（约中纬度相隔1′之间的距离）和18 000m。经计算，表层流大约为0.1～0.12m／s。这样180m 和1 800m 对应的Rossby数分别约为6.67，0.667，处于中尺度的范围，18 000m 对应的 Rossby数约为0.066 7，处于大尺度的范围。

假定Hoenikker数为0，作为对比实验，分别取不考虑Stokes漂流时和Langmuir数为0.3时2种情况进行研究。具体设置如表1所示。

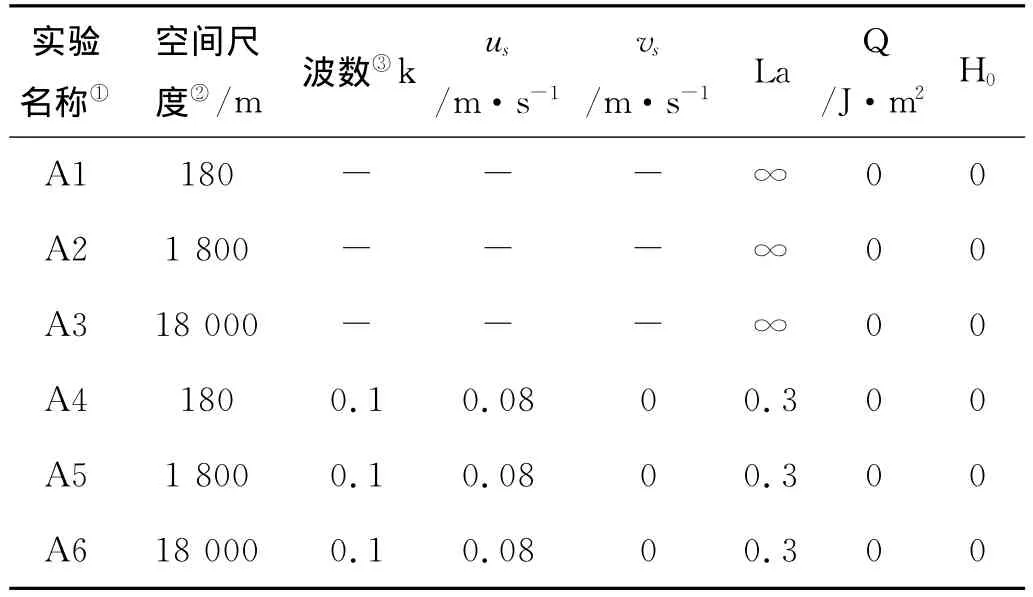
表1 空间尺度的变化对应的实验设置Table 1 Experiment settings according to diversity of spatial scales

图1为计算达到稳定后，不同尺度下混合系数和湍动能的垂向变化曲线。从中可以看出，3种空间尺度下，无论是不考虑Stokes漂流的情况还是Langmuir数为0.3的情况，混合系数和湍动能的曲线几乎都是重合的。这说明在混合方案等外部条件不变时，大、中尺度对应的混合系数km和湍动能q2变化较小。

从整个文本来说，它里面重复记录一件事情的情况很多，各种不同的类型的文字杂糅在一起，家谱、仪式方式、伦理、法律、历史故事掺杂起来，给人感觉混乱不堪。

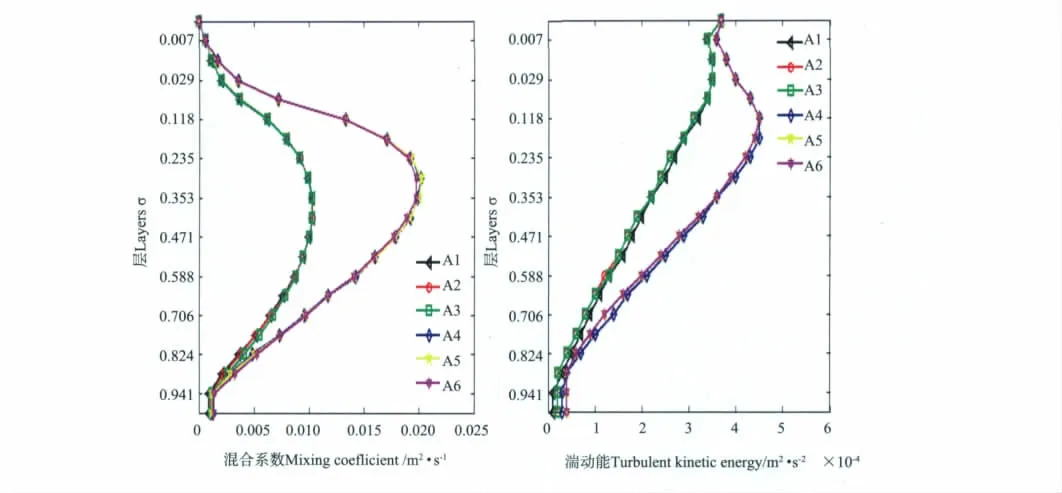
图1 混合系数km（左）和湍动能q2（右）在不同尺度下的变化曲线Fig.1 Changes of km （left）and q2（right）with three spatial scales

图2为计算达到稳定后，不同尺度下，U向平均流和V向平均流的垂向变化曲线。可以看出，对于U向平均流，空间间隔为180和1 800m时，两者对应的曲线区别很小，几乎重合。当间隔增大至18 000m时，无论是不考虑Stokes漂流的情况（实验A3）还是Langmuir数为0.3（实验A6）的情况，曲线相比前2个空间间隔都向正向移动。对于V向平均流，空间间隔为180和1 800m时，两者对应的曲线同样几乎重合。而当间隔增大至18 000m时，无论是实验A3还是实验A6，曲线相比前两者向负向移动。这说明同为中尺度下，平均流变化很小。而大尺度和中尺度的平均流之间有所变化，但是不考虑Stokes漂流和Langmuir数为0.3两种情况下，平均流的变化趋势一致。

本文的目的是研究大、中尺度下，Stokes漂流对上层海洋的影响，因此取空间间隔为1 800m具有代表意义，在下面的实验中，继续使用此间隔作为特征尺度进行研究。

图2 U向平均流（左）和V向平均流（右）在不同尺度下的变化曲线Fig.2 Changes of mean currents U （left）and V （right）with three spatial scales

3.2 Langmuir数的变化

假定空间尺度为1 800m，波数为0.1，Hoenikker数为0。随着Stokes漂流的减小，Langmuir数逐渐增大，实验设置见表2所示。

表2 Langmuir数的变化对应的实验设置Table 2 Experiment settings according to diversity of Langmuir numbers

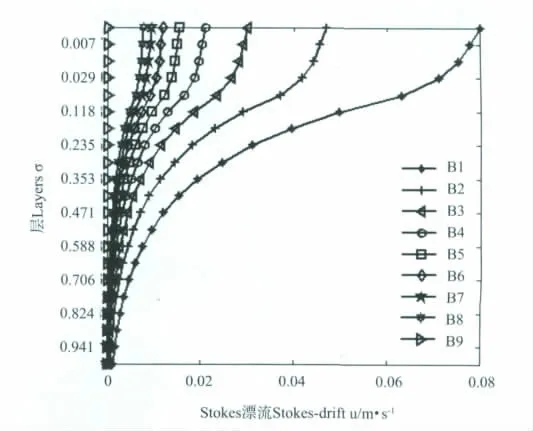
图3 Stokes漂流随Langmuir数的变化曲线Fig.3 Changes of Stokes漂流 with Langmuir numbers

图3 所示为Stokes漂流随Langmuir数的变化曲线。随着Langmuir数增大，Stokes漂流的值逐渐减小。当Langmuir数达到10时（实验B9），Stokes漂流已经减小到可以忽略不计。各层Stokes漂流呈现指数衰减的趋势，当深度达到σs＝1／2k时，此处的Stokes漂流值约为表层的0.36，σs称为Stokes漂流的影响深度。

图4（左）为计算达到稳定后，湍动能随Langmuir数的变化曲线。从中可以看出，Langmuir数为0.3时（实验B1），引起的湍动能最大。随着Langmuir数的增大，不同Langmuir数对应的湍动能数值会有重合，但总体还是逐渐减小的趋势。图4（右）所示为计算达到稳定后，混合系数随Langmuir数的变化曲线。可以看出，实验B9和实验B10的曲线是重合的，这是因为当Langmuir数增大到某一数值时，Stokes漂流已经对混合系数贡献很小，可以忽略。随着Langmuir数的减小，Stokes漂流的贡献逐渐越大，垂向不稳定性增强，混合系数增大。

图5（左）为计算达到稳定后，U向平均流随Langmuir数的变化曲线。可以看出，当Langmuir数为10时，曲线与没有Stokes漂流时的曲线是重合的，这说明此时的Stokes漂流对平均流影响已经极小。随着Langmuir数的减小，表层U 向平均流逐渐减小，这是因为在假定总漂流（拉格朗日流速UL）不变的情况下，Uo＝UL－Us，Us，所占比重增大，相应的欧拉平均流Uo就会减小。随着深度增加，U向平均流逐渐由正值变为负值，且Langmuir数越小，U 向平均流的曲线越向负向移动。图5（右）为计算达到稳定后，V向平均流随Langmuir数的变化曲线。可以看出，随着Langmuir数的减小，V向平均流的绝对值逐渐减小。且以σ＝0.35左右为拐点，V向平均流从负值变为正值。这是受科氏力f＾z×U，和“Coriolis－Stokes力”f＾z×Us共同作用的结果。

3.3 Hoenikker数的变化

Skyllingstad ＆ Denbo［5］利 用 大 涡 模 拟，考 虑Hoenikker数对“Langmuir环流”的影响。但他们只考虑了冷却情况下的影响，而没有考虑加热的情况。这是因为混合层受冷时，计算容易达到稳定，而混合层受热时，会产生分层现象，不容易稳定。本文同时考虑了热通量为正、负和无热通量下，Stokes漂流的影响效果。分别取不考虑Stokes漂流（见表3）和Langmuir数为0.3（见表4）2种情况，对应 Hoenikker数从－0.25～0.25，间隔0.05。

表3 不考虑Stokes漂流时Hoenikker数的变化对应的实验设置Table 3 Experiment settings according to diversity of Hoenikker numbers without considering Stokes drift

表4 Langmuir数为0.3时Hoenikker数的变化对应的实验设置Table 4 Experiment settings according to diversity of Hoenikker numbers when Langmuir number is 0.3

在环流模式中，实际计算海面热通量计算时，需要考虑大气反馈项的修正作用（Haney［26］）

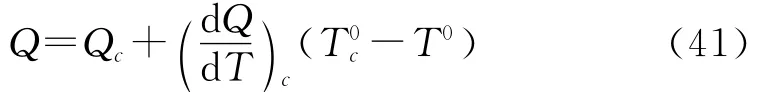
其中：下标C表示气候态平均数据；T0表示模式计算的海面温度。

由于本文旨在研究不同Hoenikker数变化下，上层混合层各个参量的变化，因此没有采用公式（41）的修正作用。这样随着热通量的增减，海水温度会有一个持续升高或降低的过程。并且Hoenikker数为负值时（热通量为负）时，混合系数随时间逐渐变大；当Hoenikker数为正值时（热通量为正）时，混合系数随时间逐渐变小，但是当计算超过6h后因为层化作用而逐渐变得杂乱无章。为了比较同一时刻海水温度和混合系数随不同Hoenikker数的变化，本文取计算开始至4小时的实验结果进行分析。

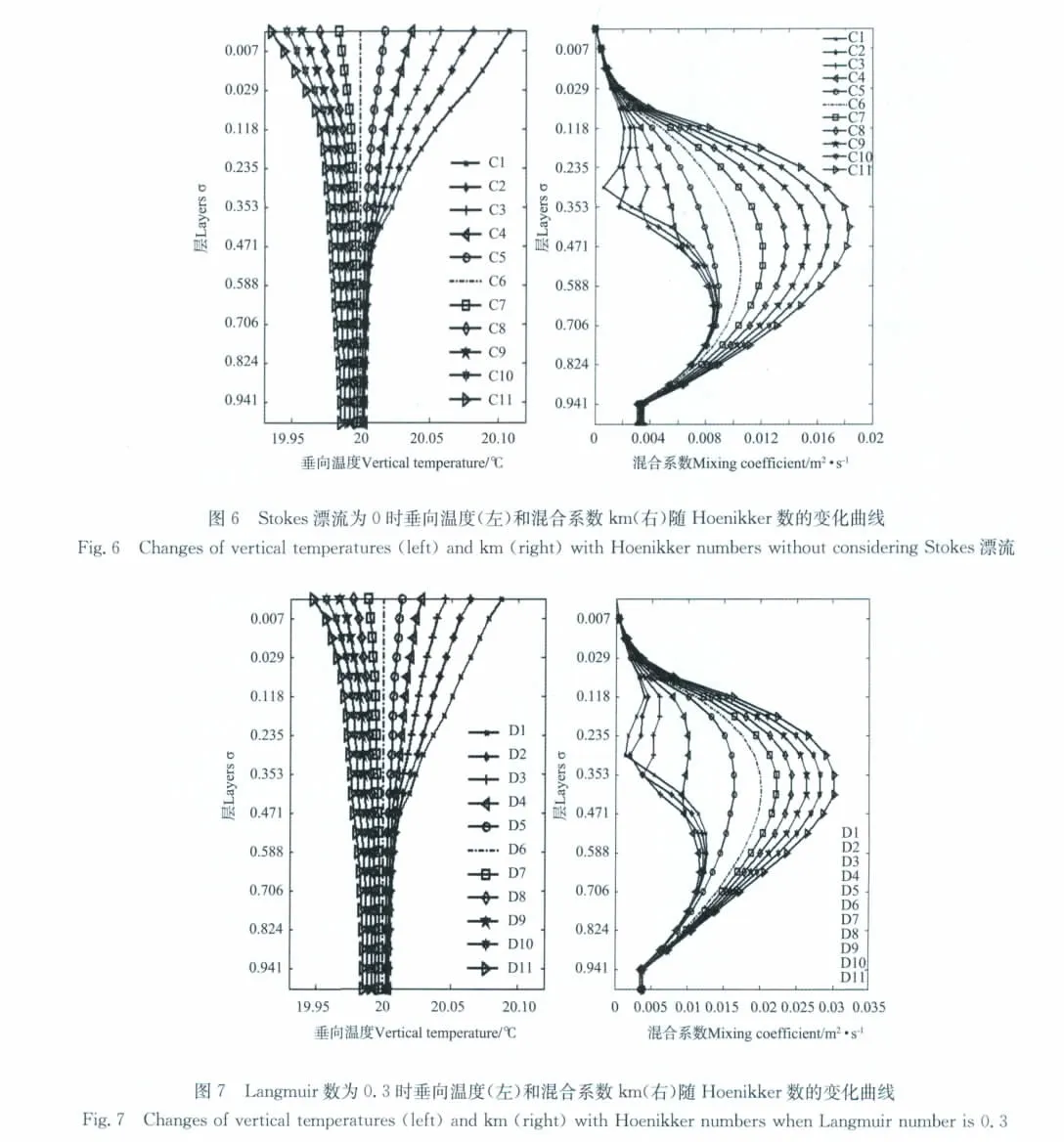
图6为不考虑Stokes漂流时垂向温度和混合系数随Hoenikker数的变化曲线。结合这2张图可以看出，Hoenikker数为负值时，温度降低，混合系数值变大，混合深度变深，这是因为温度的降低减小了海水层化效果，使海水不稳定性增强。与之相反，Hoenikker数为正值时，上层海水温度升高，混合系数值变小，混合深度变浅，这是因为温度的升高增大了海水层化现象，使海水变得更加稳定。

图7为Langmuir数等于0.3时，垂向温度和混合系数随Hoenikker数的变化曲线。结合图6可以看出，考虑Stokes漂流前后，混合系数和垂向温度随Hoenikker数的变化趋势是一致的。但是比较图6（左）和图7（左），Hoenikker数变化相同时，不考虑Stokes漂流时上层海洋温度的变化幅度（绝对值），要比Langmuir数等于0.3时的变化幅度大。这说明考虑Stokes漂流后，温度的敏感性有所减小。同时比较图6（右）和图7（右），可以看出，若Hoenikker数改变相等的量值，Langmuir数等于0.3时混合系数的变化幅度，要大于不考虑Stokes漂流时的变化幅度。这说明Hoenikker数相同时，考虑Stokes漂流后混合系数的敏感性变大。

4 结论

本文在总结前人研究的基础上，对N－S方程进行波浪平均，得到新的包括Stokes漂流影响的三维数值模型。着眼于大、中尺度，同时考虑“Stokes－Vortex力”引起的湍流混合效应和“Coriolis－Stokes力”的输运作用，将数值模型应用到三维环流模式POM中，选取参数进行理想数值实验，得到以下结论：

（1）混合方案等外部条件不变时，大、中尺度对应的混合系数km和湍动能q2变化较小。同为中尺度下，平均流变化很小。而大尺度和中尺度的平均流之间有所变化，但是考虑Stokes漂流前后，各尺度平均流的变化趋势一致。

（2）随着Stokes漂流不断增大，Langmuir数逐渐减小，垂向不稳定性增强，湍动能增强，混合系数增大。Langmuir数越小，对平均流的影响越大。

（3）Hoenikker数为负值时（热通量为负），温度降低，减小了海水层化效果，海水不稳定性增强，混合系数增大，混合深度加深。Hoenikker数为正值时（热通量为正），温度升高，增大了海水层化现象，使海水变得更加稳定，混合系数变小，混合深度变浅。

由此可见，Stokes drift不仅改变了混合层的垂向流速切面，并且影响了混合层的湍流生成和混合，进而对混合层的动力学结构乃至热力学结构有着非常重要的作用。

［1］ Stokes G G.On the theory of oscillatory waves［J］.Trans Cambridge Philos Soc，1984，8：441－455.

［2］ Langmuir I.Surface motion of water induced by wind ［J］.Science，1983，87：119－123.

［3］ Craik A D，Leibovich S.A rational model for Langmuir circulations［J］.J Fluid Mesh，1976，73：401－426.

［4］ Craik A D.The generation of Langmuir circulation by an instability mechanism ［J］.J Fluid Mesh，1977，125：37－52.

［5］ Skyllingstad E D，Denbo D W.An ocean large－eddy simulation of Langmuir circulations and convection in the surface mixed layer［J］.J Geophys Res，1995，100：8501－8522.

［6］ Mc Willianms J C，Sullivan P P，Moeng C H.Langmuir turbulence in the ocean［J］.J Fluid Mesh，1997，334：1－30.

［7］ McWilliams J C，Testrepo J M，Lane E M.An asymptotic theory for the ocean［J］.J Fluid Mesh，2004，511：135－178.

［8］ Li S，Song J B，Sun Q.Effect of Stokes drift on upper ocean mixing［J］.Acta Oceanologica Sinica，2008，27：11－20.

［9］ Uchiyama Y，McWilliams J C，Restrepo J M.Wave current interaction in nearshore shear instability analyzed with a vortex－force formalism ［J］.J Geophys Res，2009，114，C06021.doi：10.1029／2008JC005135.

［10］ Uchiyama Y，McWilliams J C，Alexander F Shchepetkin.Wave current interaction in an oceanic circulation model with a vortexforce formalism：Application to the surf zone［J］.Ocean Model－ling，2010，34：16－35.

［11］ Kenyon K E.Stokes transport［J］.J Geophys Res，1970，75：1133－1135.

［12］ Hasselmann K.Wave－driven inertial oscillations［J］.Geophys Fluid Dyn，1970，1：463－502.

［13］ McWilliams J C，Restrepo J M.The wave－driven ocean circulation［J］.J Phys Oceanogr，1999，29：2523－2540.

［14］ Wu K J，Liu B.Stokes drift induced and direct wind energy inputs into the Ekman layer within the Antarctic Circumpolar Current［J］.J Geophys Res，2008，113，C10002，doi：10.1029／2007JC004579.

［15］ Wu K J，Yang Z L，Liu B，et al.Wave energy input into the Ekman layer［J］.Science in China Series D：Earth Sciences，2008，51：134－141.

［16］ Deng Zengan，Xie Lian，Han Guijun，et al.The effect of Coriolis－Stokes forcing on upper ocean circulation in a two－way coupled wave－current model［J］.Chinese Journal of Oceanology and Limnology，2012，30（2）：321－335.

［17］ Webber J E.Steady wind－and wave－induced currents in the upper ocean［J］.J Phys Oceanogr，1983，13：524－530.

［18］ Xu Zhigang，Bowen A J.Wave－and wind－driven flow in water of finite depth［J］.J Phys Oceanogr，1994，24：1850－1866.

［19］ Sun F，Gao S，Wang W，et al.Wave－induced stress and estimation of its driven effect on currents［J］.Science in China Ser.D：Earth Sciences，2004，47：1147－1154.

［20］ Smith J A.Wave－current interactions in finite－depth［J］.J Phys Oceanogr，2006，36：1403－1419.

［21］ Lane E M，Restrepo J M，McWilliams J C.Wave current interaction：A comparison of radiation－stress and vortex－force representations［J］.J Phys Oceanogr，2007，37：1122－1141.

［22］ Sullivan P P，McWilliams J C，Melville W K.Surface gravity wave effects in the oceanic boundary layer：Large－eddy simulation with vortex force and stochastic breakers［J］.J Fluid Mechanics，2007，593：405－452.

［23］ Sullivan P P，McWilliams J C.Dynamics of winds and currents coupled to surface waves［J］.Annual Review of Fluid Mechanics，2010，42：19－42.

［24］ Holm D D.The ideal Craik– Leibovich equations［J］.Physica D，1996，98：415－441.

［25］ Kantha L H，Clayson A C.On the effect of surface gravity waves on mixing in the oceanic mixed layer ［J］.Ocean Modelling，2004，6：104－124.

［26］ Haney L R.Surface thermal boundary condition for ocean circulation models［J］.J Phys Oceanogr，1971，4：241－248.