再生废旧纤维非织造布制造蜂窝夹层结构的设计

许兰涛 王山英 粘伟诚 田雨胜 吴晓青

(1.天津工业大学先进纺织复合材料教育部重点实验室，天津，300387：2.福建鑫华股份有限公司，晋江，362241)

我国是纤维生产和使用大国，每年各类纤维及织物的消耗量超过千万吨，且多数纤维都具有不可降解性。纺织厂的边角料及废旧服装的数量非常可观，造成了浪费，对环境产生的污染也越来越严重，还暗藏着火灾等许多隐患［1-2］。利用废旧纤维纺织品制造非织造布的工艺成熟，其产品的柔韧度、厚薄度、各种性能和形状也可以自由改变［3］。再生废旧纤维的利用不仅体现出非织造布在原料应用上的环保特色，而且其生产过程也具有环保特色，甚至可达到绿色生产［4］。夹层结构复合材料是由两片坚硬的面板和轻质夹心组成，具有强度高、刚度大、密度低、导热率低和耐腐蚀等优良的性能，被广泛应用于航空航天、汽车、船舶、铁路运输以及风力发电等领域［5-8］。目前制备的蜂窝夹层结构材料一般以玻纤布、纸、棉布或铝等为原料。天津工业大学等单位突破传统观念，设计开发了以再生废旧纤维非织造布为原料制备的蜂窝夹层结构材料［9］。本文主要论述蜂窝夹层结构材料中蜂窝芯的宽厚比和蜂窝边长的设计过程。

1 蜂窝夹层结构的设计依据及平压破坏方程推导

蜂窝夹层复合材料一般是由上、下面板和夹在中间的一层比较厚的软夹芯构成。蜂窝芯的形状根据其平面几何投影，可分为六边形、菱形、矩形、正弦曲线形和加强带六边形等［10］，其中正六边形蜂窝制造简单，用料省，强度也较高，应用最广泛。本文主要是依据不同平压破坏形式对六边形蜂窝夹层结构进行设计。

1.1 平压破坏形式

蜂窝夹层结构根据其结构特征的不同，可以有三种不同的破坏形式［11］:①以斜壁失稳后最大平均应力控制破坏;②以纵壁应力达到材料压缩强度控制破坏;③以纵壁的失稳控制破坏。三种不同的破坏形式对应三种不同的破坏强度。下面就蜂窝夹层结构的三种破坏形式推导其三种破坏强度方程。

1.2 平压破坏方程的推导

判断压缩是否造成破坏要有依据，把蜂窝夹层结构简化为四边简支平板给出三种判据，根据三种破坏形式和判据可以推导出蜂窝芯子及夹层结构的平压破坏方程。

1.2.1 压缩破坏的三种判据

蜂窝夹层结构的平压破坏实际是蜂壁壁板的压缩破坏，把蜂壁壁板简化为四边简支板，根据板的弹性屈曲理论，在理想弹性状态下，蜂壁的破坏应力有:

临界失稳应力［12］:

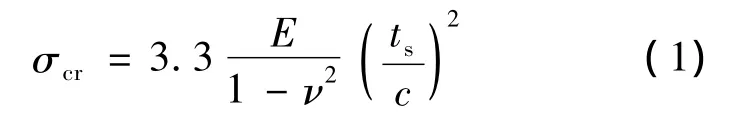
极限载荷:

失稳后最大平均应力:

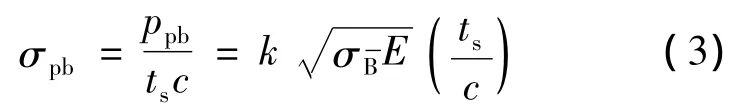
式中:E——材料的压缩模量;

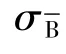
ts——蜂壁厚度:

c——蜂窝边长;

ν——泊松比:

k——常数。

1.2.2 蜂窝芯子三种平压破坏方程

根据三种破坏形式以及压缩破坏的三种判据推导平压破坏方程。

(1)以斜壁失稳后最大平均应力控制破坏的平压方程［11］

平压破坏方程为:

式中:σsmax——蜂窝芯子壁承受的最大平均应力。

(2)以纵壁应力达到材料压缩强度控制破坏的平压方程

平压破坏方程为:

(3)以纵壁的失稳控制破坏的平压方程

平压破坏方程为:

1.2.3 蜂窝夹层结构与芯子的关系

从蜂窝夹层结构复合材料中截取一个结构单元作为代表，说明蜂窝夹层芯子与结构板材的关系，如图1所示。图中c和d表示蜂窝边长，θ表示芯子斜壁与板材间的夹角。

图1 蜂窝夹层结构代表单元(俯视图)

由力的平衡可知，夹层结构平压应力和蜂窝芯子壁压应力之比与其面积成反比，故:

蜂格为正六边形:c=d，θ=60°，则:

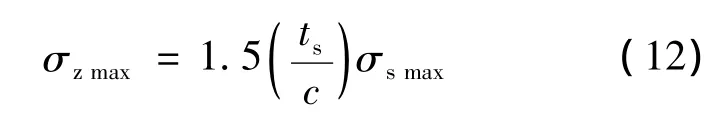
式中:σzmax——夹层结构所承受的最大平均应力。

1.2.4 蜂窝夹层结构的平压强度

根据蜂窝芯子的平压破坏强度公式(4)、公式(5)、公式(6)以及蜂窝夹层结构平压强度与芯子平压强度的关系公式(12)得到蜂窝夹层结构板材的平压强度:

2 非织造布蜂窝夹层板材的设计

2.1 宽厚比的设计

蜂格为正六边形:c=d，θ=60°。

将上述参数代入平压破坏方程，得:

由此可以得出:

2.2 蜂窝壁边长的设计

表1 时蜂窝边长和厚度的取值

3 结语

［1］ 吴晓青，邱冠雄，李嘉禄，等.废旧纤维制造装饰板材的研究［J］.新型建筑材料，2002(5):44-45.

［2］ 周文聪，张贤，张铁江，等.废旧纤维回收技术及原理［J］.纺织科技进展，2010(6):18-22.

［3］ 王延熹.非织造布生产技术［M］.上海:中国纺织大学出版社，1998:389，431.

［4］ 牛海涛，周华，郭秉臣.非织造布在环保领域的应用［J］.北京纺织，2005，26(1):11-14.

［5］ BELOUETTAR S，ABBADI A，AZARI Z，et al.Experimental investigation of static and fatigue behaviour of composites honeycomb materials using four point bending tests［J］.Composite Structures，2009，87:265-273.

［6］ QIAO Pizhong，YANG Mijia.Impact analysis of fiber reinforced polymerhoneycomb composite sandwich beams［J］.Composites:Part B，2007，38:739-750.

［7］ QIAO Pizhong，FAN Wei，JULIO F.Optimization of transverse shear module for composite honeycomb cores［J］.Composite Structures，2008，85:265-274.

［8］ CHEN Zheng，YAN Ning，DEND J.Flexural creep behavior of sandwich panels containing kraft paper honeycomb core and wood composite skins［J］.Materials Science and Engineering A，2011，528:5621-5626.

［9］ 孙洪强，粘伟诚，王山英，等.利用废旧纤维制备非织造布蜂窝夹层复合材料及其性能研究［J］.产业用纺织品，2013，31(1):21-25.

［10］范秋习.蜂窝夹层复合材料［J］.北京轻工业学院学报，1998，16(2):77-81.

［11］张汝光.玻璃钢蜂窝夹层结构的平压破坏形式和强度预测［J］.玻璃钢，1999(2):1-7.

［12］美国全国航空和搴宇宙航行局.结构稳定性手册［M］.卫星.北京:国防工业出版社，1972:26-29.

［13］周祝林.玻璃钢夹层结构制造——性能及设计简介［J］.玻璃钢，1980(4):26-33.