不同水平男子跳高运动员起跳腿空间夹角的运动学分析
王 鹏 王继艳
(曲靖师范学院体育学院,云南曲靖 655011)
1 前言
背越式跳高起跳脚着地瞬间,小腿在空间中会形成两个重要的角度,即小腿与横杆垂直面夹角(∠α)和横杆矢状面(∠β)夹角。∠α的存在是正确弧线助跑的结果,它使身体以内倾的姿势进入起跳,可以为身体获得旋转过竿的的动量,而且保证运动员垂直起跳而不会过早倒杆;∠β使身体在起跳开始时处于一种后仰的的状态,为起跳缓冲和身体重心速度的转化提供基础。这两个角度在随着起跳的完成逐渐减小,其大小决定着起跳的效果以及离地后身体的运行轨迹,适当的两角度值使运动员蹬伸前处于合理的身体姿态,不仅能使更多的动能通过肌肉的“退让”工作,转化为压紧身体的弹性势能,对提高身体重心垂直速度也有重要的影响。国内学者对于这方面的研究很少[1]。因此,本文通过分析不同水平运动员的技术录像,对这两个角度在不同的起跳高度上的变化情况进行分析,以及起跳成功与失败时两角度的变化进行分析,找出合理角度范围和影响因素,为训练和教学提供合理的建议,丰富跳高技术的理论研究。
2 研究对象与方法
2.1 研究对象
高水平选手选取2008年6月26日在江苏省举行全国田径大奖男子跳高比赛的前8名(表1),一般水平选手为2011年9月云南省第六届大学生运动会男子跳高决赛的前八名(表2)。
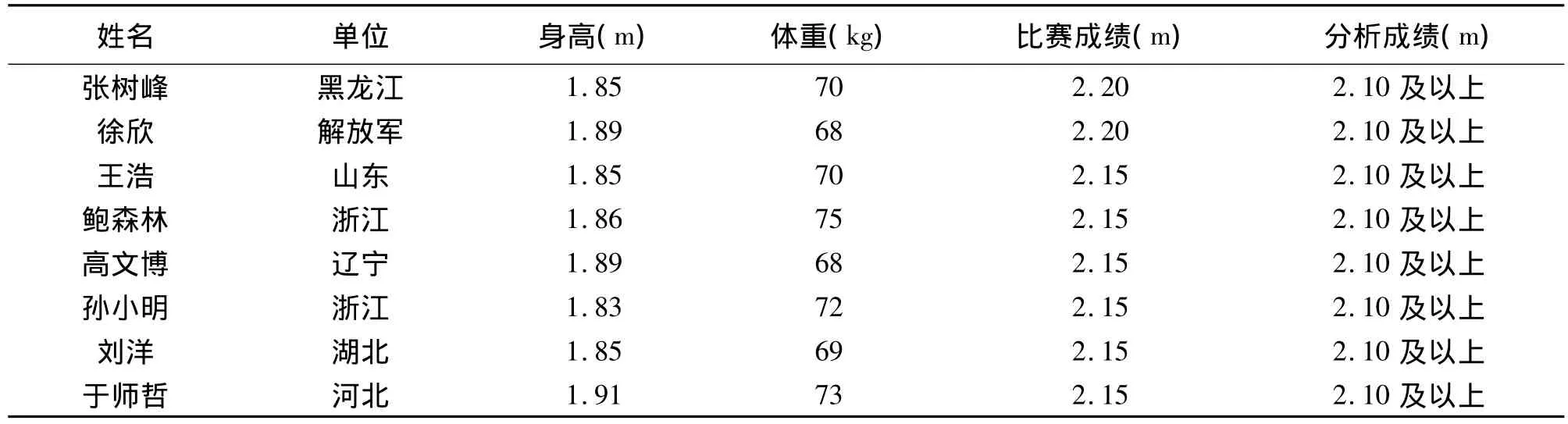
表1 高水平研究对象基本情况一览表
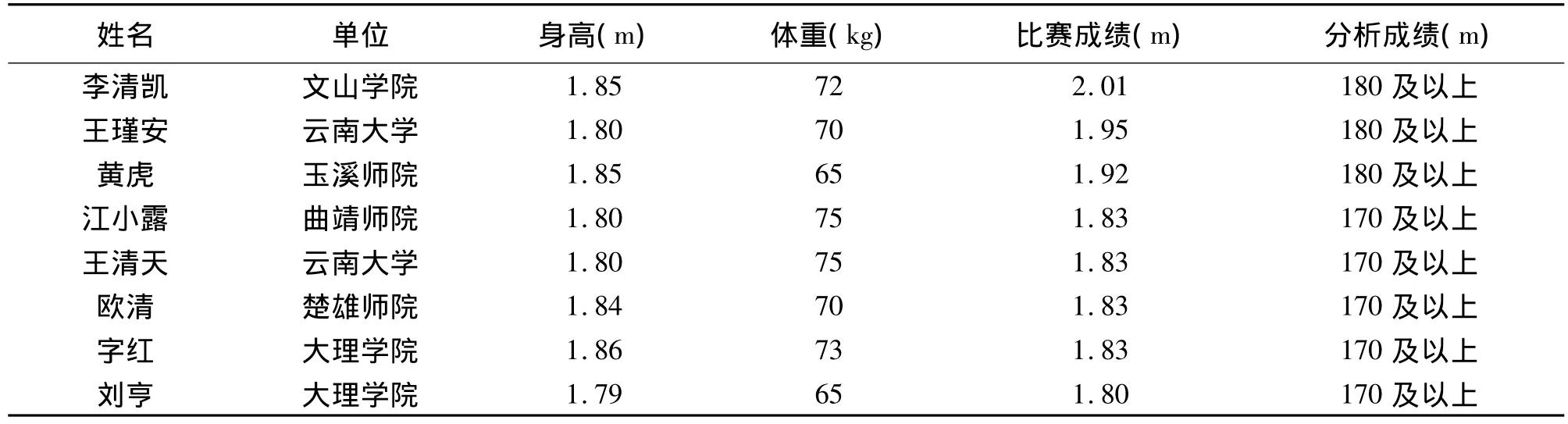
表2 一般水平研究对象基本情况一览表
2.2 研究方法
2.2.1 文献资料法
根据研究需要,通过中国期刊网,查阅相关资料,为研究提供理论依据。
2.2.2 录像拍摄法
高水平组拍摄采用两台AG-DVC180常速摄像机以50帧/秒的速度对研究对象最后三步助跑及起跳的完整技术录像。两台摄像机主光轴距起跳点14m,机高为1.20m,两机主光轴夹角在90度间,比赛前后分别拍摄爱捷三维辐射立体框架。一般水平组拍摄参数同高水平组一致。
2.2.3 影像解析法
使用Ariel运动解析系统对视频进行量化处理,采用日本松井秀治人体惯性参数模型,并依据人体模型的标准和研究需要选取19个关节点,对跳高整个技术过程进行解析处理,对解析数据通过低通数字滤波法进行平滑处理,平滑系数为6,将获取的原始数据指标保存到EXCEL软件中。
2.2.4 数理统计法
利用SPSS12.0统计软件对原始数据进行统计学处理。
3 分析与讨论
3.1 不同水平运动员两角度随起跳高度的变化
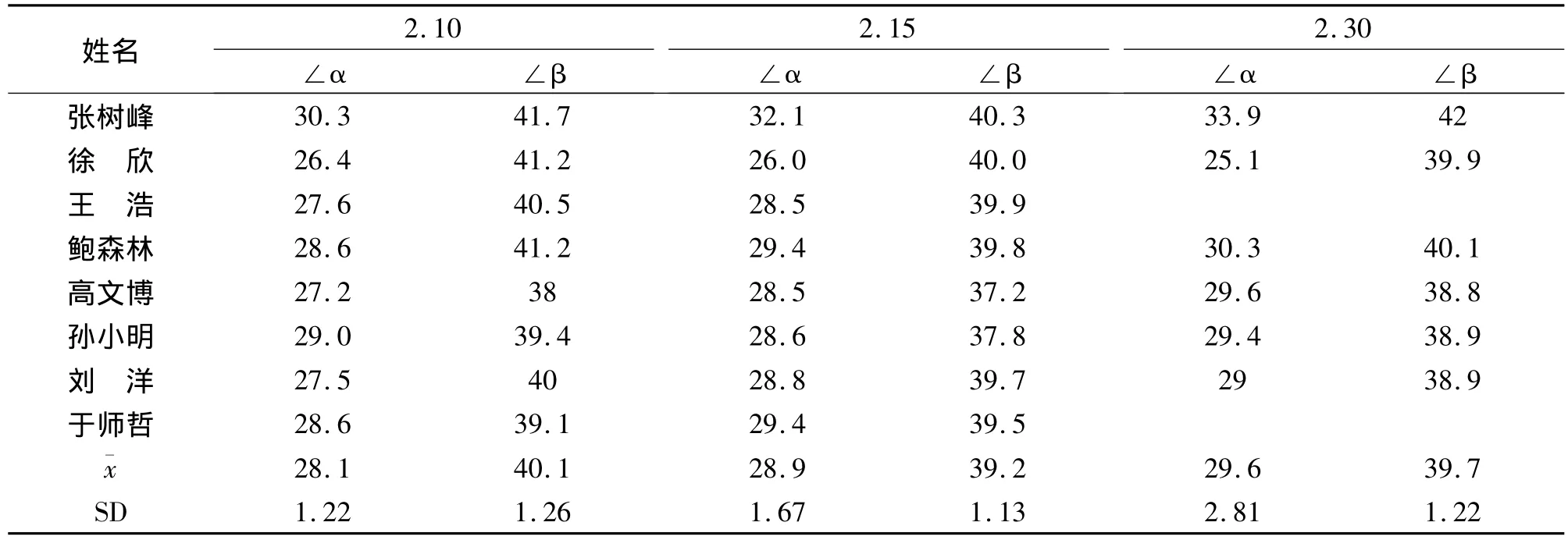
表3 高水平运动员两角度在不同高度上的值(°)
关于起跳着地瞬间运动员身体空间角度的研究,主要集中在身体内倾角方面,起跳腿的空间夹角研究较少,但是跳高的起跳动作都是以起跳腿为轴的空间运动,因此对起跳腿的空间夹角进行分析同样具有重要的意义[2,3,4,5]从表 3 可以看出∠α 随着起跳高度的增加而逐渐增加,在2.10 m-2.20m高度范围内,∠α均数增加了2.6度。对2.10 m-2.15m∠α的值进行差异性检验,t= -2.727,p<0.05,说明在高水平运动中2.10 m-2.15m的高度上∠α有显著性差异,用相同的方法也可以得出2.15m-2.20m中∠α也具有显著性差异。∠α在三个高度上的变化范围不是很大,但是有些个体的差异比较大,在2.10 m时张树峰与王浩的∠α相差达4度,说明在高水平运动员中由于自身的技术特点,个别运动员∠α的差异很明显。高水平运动员在所有的跳次中∠α主要集中在28.5,上下波动范围1.5度,总体上看∠α的波动不大,这反映出高水平运动员技术比较稳定的特点。
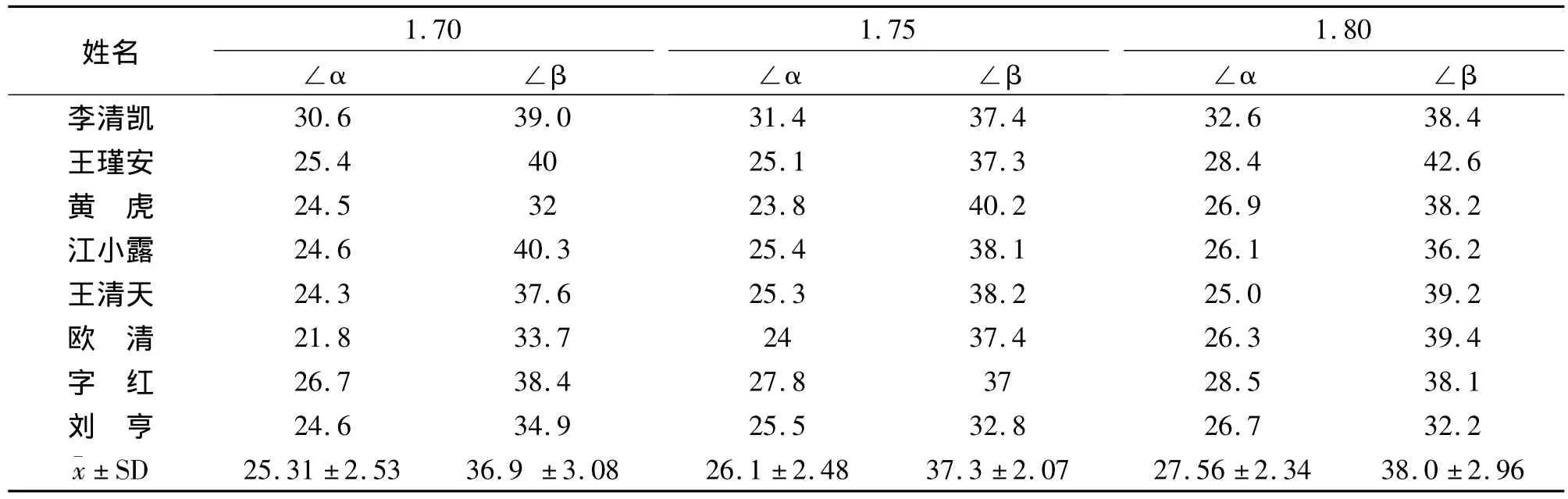
表4 一般水平运动员两角度在不同高度上的值(°)
∠β随着起跳高度的变化也有所波动(表3),但是从三个高度均值来看,变化范围比较小,从离散程度来看也要比∠α的离散程度小,同时也没有呈现出明显的变化趋势。从每名运动员变化值来看,大多数运动员∠β的变化都在2度以内。高水平运动∠β在所有跳次中的值集中在39度,上下波动范围为1.5度。对2.10 m-2.15m高度的∠β值进行差异性检验,t= -2.364,P>0.05说明在高水平运动中不同的高度∠β差异不显著,2.10 m-2.15m高度∠β差异也不显著。由以上检验可以得出,∠β的值随高度的增加没有明显的递增或递减趋势。
对一般水平运动员∠α值进行分析(表4),从总体上看1.70m-1.80m∠α的均值是不断增大的,在相同高度上,比如1.70m时,∠α的最大值与最小值之差达到8.9度,个体之间相差明显要比高水平运动员大,说明参加一般水平选手技术水平差距比较大。个体在不同高度上,∠α的值变化也比较明显,比如欧清1.70m-1.80m三个高度∠α的值分别为21.8、24、26.3,最高值与最低值相差了3.5度。从∠α的均值的离散程度来看,也要远高于高水平运动员的值,可以说明一般水平运动员的技术稳定性与高水平差距明显。
对一般水平运动员的∠β值进行分析,从1.70m-1.80m三个高度∠β的均值来分析,随着高度的增加∠β的均值也稍有增加,两高度之间大约相差0.6度。1.70m-1.80m三高度的∠β值的标准差大于高水平运动员。可以看出一般水平运动员∠β波动范围较大,稳定性比高水平运动员差。对1.70m与1.75m两组∠β进行的差异性检验,t=-0.113,P>0.05,说明这两个高度∠β差异不显著,1.75m-1.80 m两个高度∠β差异也不显著。由以上检验可以得出,一般水平运动员∠β在不同高度的差异较小,与高水平运动员相似。分析个体∠β的值可以看到相差较大,如在1.80m时王瑾安与刘亨∠β分别为42.6、32.2,相差了10.4度,在高水平运动员则差异较小。
从以上分析可以看出,∠α在高水平和一般水平运动员中都是随起跳高度的增加而逐渐增大,变化趋势相同,高水平运动员∠α明显高于一般水平,这说明在较高高度上适当的增加∠α有利于成功试跳。∠β无论是在高水平运动员中还是在一般水平运动员中在相临的高度上差异都较小,但是从整体上看高水平运动员∠β更大,不同水平之间差异非常显著。
3.2 两角度在不同水平运动员中试跳成功与失败时变化情况的分析

表5 高水平运动员成功与失败时两角度的值(°)

表6 一般水平运动员成功与失败时两角度的值(°)
在高水平运动员中选取六名运动员,这六名运动员试跳成功与失败时的起跳高度不同,但是每名运动员选择的试跳成功与失败是同一高度。高水平运动员起跳高度在2.10米及以上。一般水平运动员选取跳次方法相同,高度在1.70米以上。
由表5可以看出高水平运动员两角度的值在成功与失败时存在差距,绝大多数运动员成功时的值比失败时大,这种差距大约在1.5-2度之间,有个别运动员差距稍大。通过对对试跳成功与失败时的∠α和∠β进行差异性检验,P值分别为0.031和0.033,都小于0.05,有显著性差异,说明高水平运动员适当增大两角度有利于顺利完成起跳。
一般水平运动员两角度的变化趋势与高水平运动员相似(表6),在变化幅度上存在差别。从整体上来看试跳成功时∠α的均值比试跳失败要大,均值之差是1.3度,这一数值要比高水平运动员的差值小,∠β的均值变化同∠α相似。通过对试跳成功与失败时的∠α和∠β进行差异性检验,P值分别为0.042和0.001,∠α有显著性差异,∠β有非常显著性差异,说明增大∠β对一般水平运动员更有意义。
3.3 重心速度与两角度关系的分析
3.3.1 两角度与起跳腿着地时刻重心水平速度的相关性分析
首先,对高水平运动员重心水平速度与∠α的值进行皮尔逊相关系数检验,V0与∠α的检验结果是r=0.879,P<0.01,说明在高水平运动员起跳脚着地时重心水平速度与∠α有显著性的正相关,也就是说在高水平运动员在一定的范围内∠α随V0的增加而有增大的趋势。

表7 不同水平运动员起跳脚着地时刻重心水平速度与两角度一览表
V0与∠β值的检验结果显示在高水平运动员中最后一步重心水平速度与∠β的值并不存在显著的相关,原因是因为影响∠β值的因素比较多,如助跑时的弧线曲率,最后一步步长,手臂的摆动速度,着地时刻膝关节的弯曲程度等因素对∠β值都会有不同程度的影响。但是从理论上来说当助跑速度达到较大的值时相应的增大∠β值将有效的缓冲身体向前的冲力,减小身体腾起时的重心水平速度,使助跑速度更多的转化到垂直速度上。在高水平运动员中张树峰与徐欣就是很好的例子,他们都是高水平运动员中最后一步重心水平速度较快的运动员,尤其是张树峰是所选运动员中最后一步重心水平速度最快的运动员,而且两位运动员也是本次比赛中成绩最好的两名运动员,两名运动员∠α,∠β的值也要比其他高水平运动员的稍大。
对一般水平运动员的V0与∠α,∠β进行皮尔逊相关系数检验,V0与∠α的检验结果是 r=0.650,P<0.01,说明在一般水平运动员最后一步重心水平速度与∠α有显著性的正相关,而且这种趋势比较明显。这一点与高水平运动员的检验结果比较相似,进一步证明V0与∠α成显著性的正相关。这一点在取得本次比赛第一名的数据中体现的比较明显,李清凯是本次比赛中助跑速度最快的运动员,两角度的大小接近优秀运动员,尤其是∠α的值要比参加本次比赛的其他运动员大。对一般水平运动员的V0与∠β的值进行皮尔逊相关系数检V0与∠β的检验结果是r=0.000,P >0.05,说明在一般水平运动员最后一步重心水平速度与∠β没有显著性相关,高水平运动员情况相似。
通过以上的分析,可以得出在不同水平运动员中最后一步重心水平速度与∠α成正相关,与∠β没有显著性相关,从整体上来分析在一定的范围内∠α和∠β的值随速度的增加而增加。
3.3.2 ∠α在速度转化中作用的分析
本文所研究的∠α与起跳脚着地时刻的内倾角存在着一定的相关性,起跳脚着地时刻的内倾角是指起跳脚着地瞬间身体重心朝助跑弧线圆心倾斜方向与地面所形成的角度,从理论上讲本文研究的∠α与这一时刻的内倾角成负相关。离地时刻垂直速度在背越式跳高起跳中是随身体重心的不断上升而增大的。由于背越式跳高弧线助跑的作用,由内倾转化为竖直的过程就是∠α的值变化为零的过程,由内倾变为竖直过程中身体重心不断加速上升,使垂直速度加速增大。适度的∠α的值使身体重心保持在一个合理的范围内,能有效的增加起跳的工作距离;使身体由内倾变为竖直过程中身体重心不断加速上升,能有效的增加垂直速度。如果起跳脚着地时刻∠α的值较小,身体重心就会过早、过快通过起跳点,导致运动员的身体倒向横杆,使起跳失败。
3.3.4 对∠β在速度转化过程中所起作用的分析
背越式跳高助跑速度的转化有两种方式,第一种是缓冲阶段起跳腿伸肌获得的弹性势能,另一种方式是在起跳阶段由平动动能向转动动能的转化,它是依靠在起跳过程中人体的制动所产生的以起跳腿的支撑点为中心的转动[6]。根据材料力学的观点,人体如果在起跳开始瞬间以向后倾斜的刚性姿态形成强有力的支撑,那么助跑的平动动能则更容易转化为重力势能,也就是说在这一过程中∠β的大小对助跑速度的转化有着一定的影响。
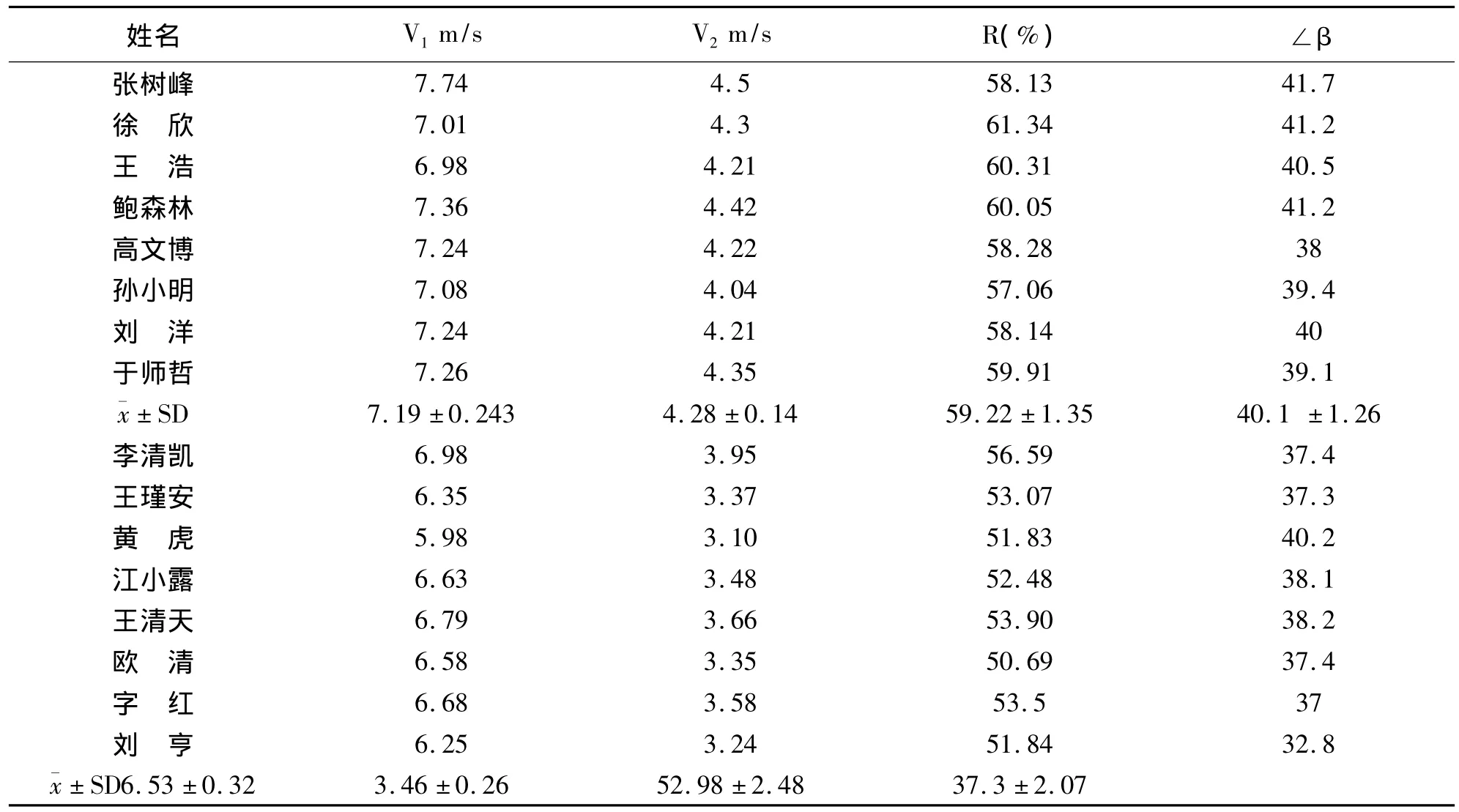
表8 不同水平运动员重心速度及速度转化率一览表
根据动量定理和几何原理,不难推断出助跑水平速度与垂直分量(仅由转动引起的)之间的关系,用公式表示为:Vz=V0/tanβ(Vz为垂直分量,V0为水平速度,可见由转动引起的垂直分量与水平速度和∠β的正切值成反比。也就是说,在一定的范围内∠β角越小,向上的垂直分量越大。这里值得一提的是,不能因垂直分量与∠β存在的这种关系而刻意地减小∠β,因为∠β过小会影响起跳的制动效果,从而影响助跑平动动能向起跳腿伸肌弹性势能的转化,另一方面还有可能错失蹬伸良机,从而使身体过早地倒向横杆。∠β过大会加大地面的水平制动力,使起跳腿的负担过重,从而使身体出现"下塌"现象,影响后继的蹬伸效果,所以∠β的大小应根据自身的身体条件在运动实践中调整。
经检验不同运动员起跳着地时的重心水平速度成显著性差异(表8),一般水平运动员与高水平运动员离地瞬间重心垂直速度的值,以及速度转化率成非常显著性差异。不同水平运动员速度转化率差异的主要原因是因为一般水平运动员起跳离地瞬间重心垂直速度低造成的。对所有运动员速度转化率的值与∠β进行相关性检验,得到r=0.7130,P<0.01,说明速度转化率的值与∠β的值成正相关,即∠β的值较大时速度转化率也相对较高。
3.4 起跳脚着地时刻着地点与横竿垂直面的距离(L)对∠α影响的分析
对表9中高水平运动员L值与∠α进行皮尔逊相关系数检验,得出r=0.617,P<0.05,呈显著性正相关,说明∠α与L具有一定的相关性,在大多数情况下∠α随L值的增加有所增大,但L的值应该在一个有效的范围之内,超过了L值的最大范围,∠α与L的相关性就没有意义了。通过对高水平运动员的录像进行观察,也可以发现同一名队员在相同的高度上如果有两次或三次试跳,成功试跳的L值与∠α要稍大于失败的试跳值,∠α的值差距大约在1-3度之间,所以适当的增加L与∠α有利于成功试跳。通过对表10中的L与∠α进行皮尔逊相关系数检验,得出r=0.874,P<0.01,呈显著性正相关,说明∠α的值与L的值具有一定的相关性,在大多数情况下∠α随L的增加而增加。一般水平运动员L值偏小(以0.70m为界,小于0.70m为偏小)时,∠α的值也较小,伴随着失败的跳次较多。
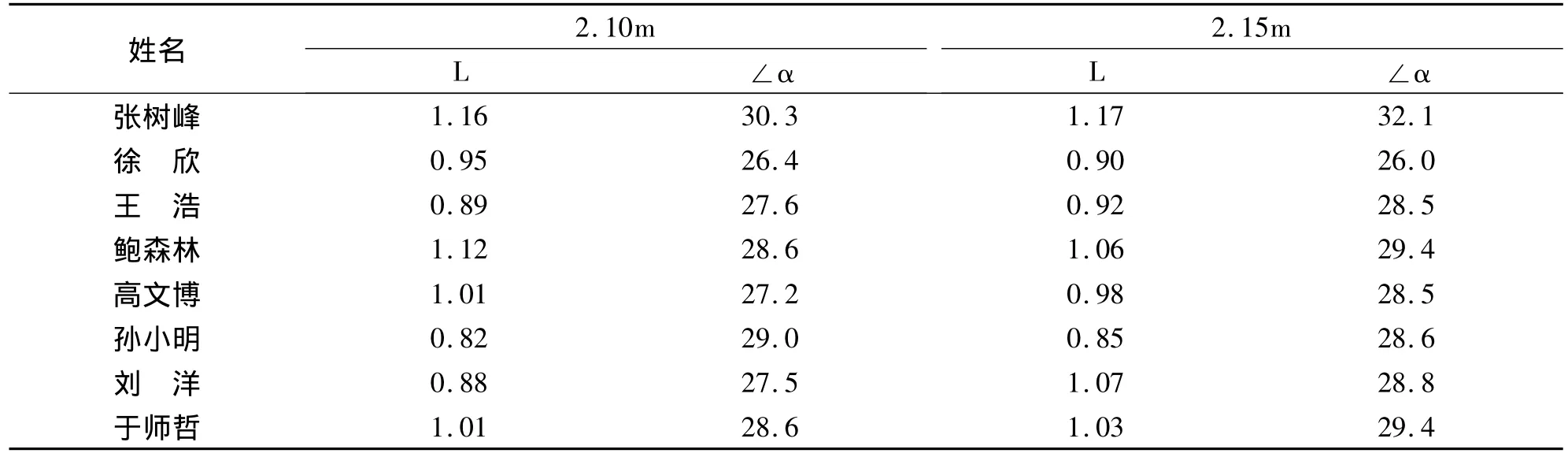
表9 高水平运动员起跳点距横杆距离与∠α一览表
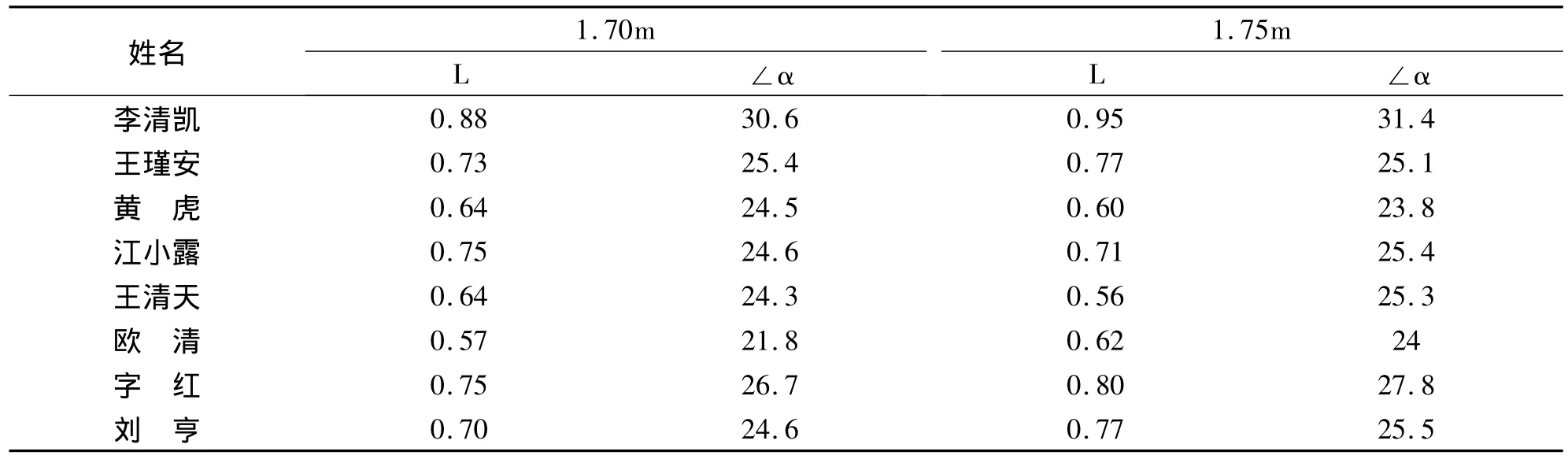
表10 一般水平运动员起跳点距横杆距离与∠α一览表
通过上述分析,不同水平运动员的∠α同起跳点与横竿垂直面的距离有一定的关系,一般水平运动员更为明显,主要是因为起跳点与横竿垂直面的距离偏小,会对运动员的心理有一定的影响,使其不敢做动作,动作的幅度就会有所减小,这样对∠α影响就会更明显,使∠α有所减小,这样以来就减弱了这一角度在起跳中应有的作用,容易造成偏心起跳,以及身体过早的倒向横杆。
4 结论
1.从整体上来看高水平运动员的∠α和∠β明显高于一般水平运动员。不同水平运动员∠α随起跳高度的变化成相同的趋势,∠α随起跳高度的增加而逐渐增加。无论是在高水平运动员中还是一般水平运动员的∠β在相临的高度上差异都较小。高水平运动员在不同的跳次中这两角度的变化幅度较小,一般水平运动员的变化幅度较大,这说明一般水平选手的起跳技术稳定性较差。
2.不同水平运动员试跳成功时的两角度都要比失败时大,经检验在不同水平运动员中起跳成功时与起跳失败时两角度的值都成显著性差异,说明在不同水平运动员中,适当的增大两角度都有利于成功完成试跳。通过对一般水平运动员试跳成功与失败时的∠α和∠β进行差异性检验,∠β有非常显著性差异,增大∠β对成功试跳更有意义。
3.不同水平运动员中最后一步重心水平速度与∠α成正相关,对∠β的值与速度转化率之间的关系进行分析,∠β的值与速度转换率成正相关。在一定的范围内适当的增加∠β的值将有利于速度的转化。
4.不同水平的运动员∠α的值同起跳脚最后一步着地时着地点与横竿垂直面的距离成正相关,这种相关性在一般水平运动员更明显,原因是一般水平运动员起跳点与横竿的距离偏小,会影响到∠α的值。
[1]黄玉保,邓重生,邓京捷.不同等级女子跳高运动员起跳腾空的运动学分析[J].山东体育学院学报,2006,22(3):75-76.
[2]汪丽华.对我国优秀男子背越式跳高运动员起跳技术的三维运动学分析[J].中国体育科技,2001,37(8):36-38.
[3]黄建军.背越式跳高技术类型新划分及运动学比较研究[J].北京体育大学学报,2004,27(3):408-409.
[4]林明,娄春风,韩敬.背越式跳高有关技术理论及训练方法的思考[J].西安体育学院学报,2003,20(3):75-76.
[5]宋跃先,彭支玉,王舟舟.跳高技术的运动生物力学分析[J].福建体育科技,2003,22(5):15-16.
[6]闫之朴.跳高助跑速度转化率的生物力学研究[J].山东体育学院学报,2005,21(6):72-73.

