悬移质泥沙的垂线分布

莫 磊，李瑞杰，2，李佳芮，刘华锋

(1.河海大学海岸灾害及防护教育部重点实验室，江苏南京 210098;2.河海大学环境海洋实验室，江苏南京 210098)

悬移质泥沙的浓度分布理论多种多样［1］，但都可以统一到扩散理论的形式，不同点主要表现为扩散系数中考虑的主要影响因素和影响方式的差别。扩散理论的关键是合理确定扩散系数，由于泥沙问题的复杂性，扩散系数的确定经常带有半经验性，通常引入施密特数Sc(Sc=vt/εs)或修正系数β(β=1/Sc)，认为紊动扩散系数εs正比于水流紊动黏性系数vt［2］。进一步假定水流质点的紊动扩散与水流动量的紊动交换过程类似，紊动扩散系数等于水流紊动黏性系数。在研究含沙量沿垂向分布以及紊流计算中，经常要用到水流的紊动黏性系数［3］。基于有限掺混长度理论，不同掺混长度的表达式对应着不同的水流紊动黏性系数［4］。由于不同区域的泥沙特性不一样，因此考虑泥沙垂线分布时也要考虑到不同区域的泥沙特性［5-7］。泥沙垂线分布公式的形式很多［8-11］，其中Rouse提出的公式应用最多，但Rouse公式有一定的局限性。笔者拟从水流的应力分析入手，对实测资料进行最小二乘拟合，期望得出新的掺混长度公式，进而导出新的悬沙垂线分布公式以弥补Rouse公式的一些缺陷。

1 紊动黏性系数

1.1 应力分析

根据紊流理论，切应力由两部分组成:

其中

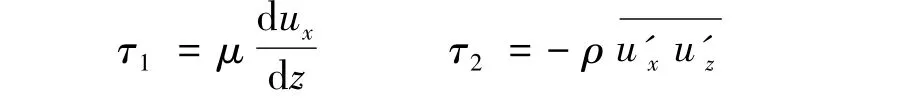
式中:τ1——黏滞切应力;τ2——紊动切应力;μ——水流的动力黏性系数;ux——顺流向的速度分量;ρ——水的密度;u'x——x方向的脉动流速;u'z——z方向的脉动流速。

对于二维均匀流，τ沿垂线的分布呈线性变化:

其中

式中:τ0——床面切应力;z——垂向位置坐标(z轴的正方向与重力方向相反)，在床面上时取z=0;h——水深;u*——摩阻流速。

紊流中，在黏性底层以外的流区，满足:

根据Prandtl的混合长度理论，τ2又可表示为

1.2 掺混长度

Prandtl假设掺混长度的表达式为l=κz，其中κ为卡门常数。而Rouse公式中，采用二维均匀流的切应力垂线分布τ=τ0(1-z/h)，得到紊流掺混长度公式为

根据Einstein和Chien的泥沙试验资料，采用最小二乘法拟合出一条平滑的曲线。该曲线的表达式为

式中A为待定系数，A的拟合结果为0.172375。

将Prandtl及Rouse采用的紊流掺混长度公式与式(6)进行比较(图1)，可知Prandtl掺混长度在整个垂线方向为线性形式，这与实际不符。同样，Rouse公式的掺混长度在水面处等于零，这也与实际不符。

再将Prandtl，Rouse和式(6)的紊流掺混长度与试验资料进行比较(图2)，可知式(6)结果与Einstein和Chien的泥沙试验资料最切合。

1.3 紊动黏性系数的计算

1887年Boussinesq类比层流提出了紊动黏性系数νt的概念，根据其假定:

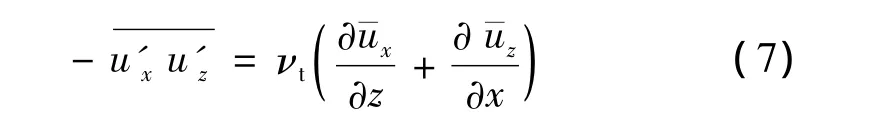
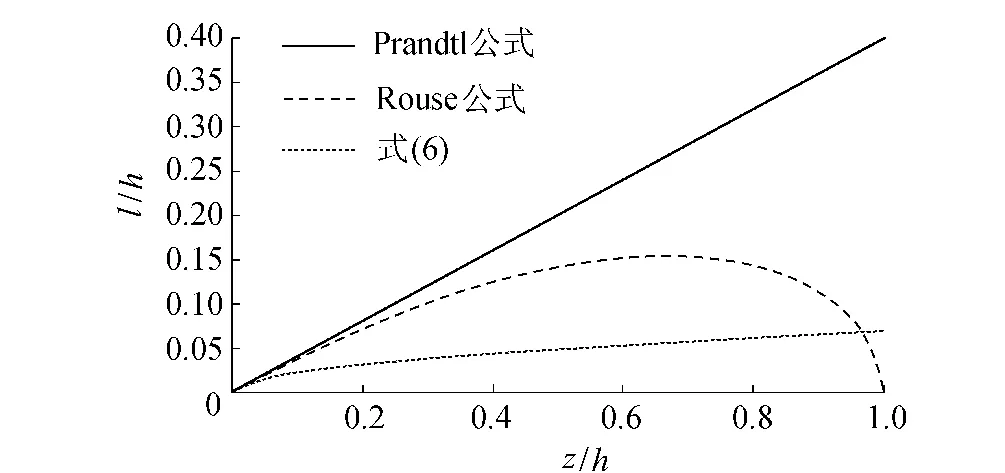
图1 Prandtl和Rouse采用的紊流掺混长度与式(6)结果的比较Fig.1 Comparison of Prandtl and Rouse’s mixing length with Eq.(6)

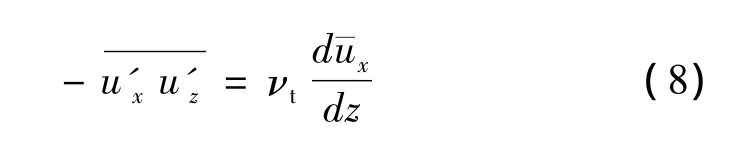
将式(3)代入式(1)，并将 τ0=ρ代入，联立式(8)可得

图2 Prandtl，Rouse及式(6)的紊流掺混长度与Einstein和Chien试验资料的比较Fig.2 Comparison of Prandtl and Rouse’s mixing length，and Eq.(6)with Einstein and Chien’s test data

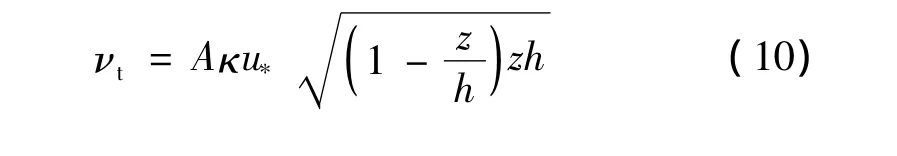
2 悬沙垂线分布公式

式中:ω——泥沙颗粒在静止清水中的沉降速度;c——含沙量;εs——泥沙颗粒交换系数，取εs≈νt，可得

悬移质在水流中处于平衡状态时应满足的质量守恒方程为

式中ca为z=a处的含沙量。

而Rouse公式为

其中

瓯江口的泥沙为黏性沙，根据Krone发现的泥沙沉速随着含沙量的增加而增加的规律［12］，认为可取

式中K为经验系数，取为0.001。在已知u*和ω的情况下，即可求得Rouse数。

取Rouse数等于1时，Rouse公式和式(12)结果的比较如图3所示。结果显示，式(12)与Rouse公式的相关系数达到0.9628，但式(12)却克服了Rouse公式所在水面处和河底部位出现的缺陷，即式(12)不仅当悬浮指标不大时所描述的水面含沙量不为零，而且当参考点取得相当小时所描述的含沙量仍不会出现等于无穷大的不合理现象。

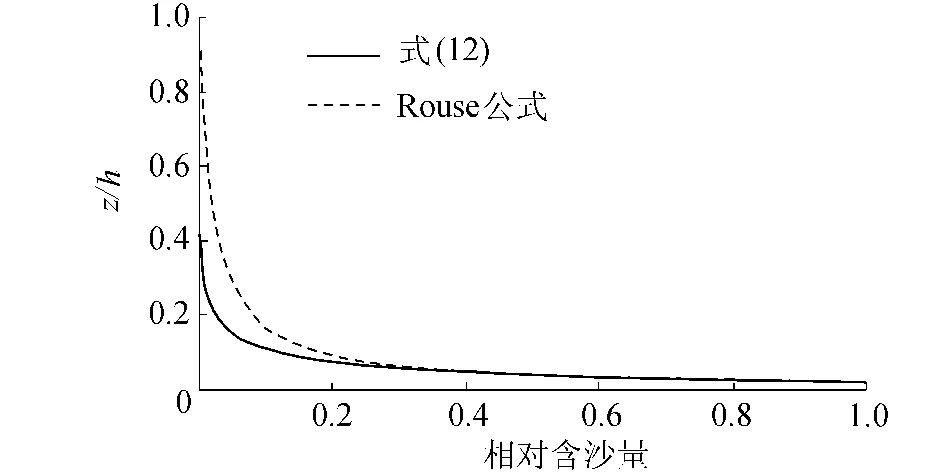
图3 Rouse公式结果与式(12)结果的比较(Rouse数为1)Fig.3 Comparison of Rouse formula and Eq.(12)(assuming Rouse number is equal to 1)

3 实测资料验证分析

选取2010年瓯江口1号和2号站点的中潮实测资料(各层含沙量)对式(12)进行分析验证(参考层取为0.2层)，小潮和大潮的结果与中潮类似。

如图4、图5所示，虽然瓯江口海域输沙量大，但含沙量都比较低，泥沙分布特征不明显，下层含沙量与上层差异不大。式(12)的计算结果与实测整体趋势一致，均能客观地反映含沙量垂线分布规律。整体上，式(12)合理地反映了整个水体的含沙量垂线分布规律。

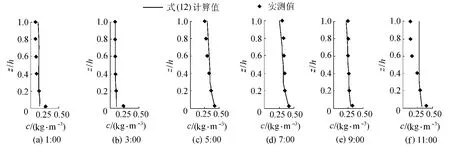
图4 瓯江1号站位(中潮)计算与实测含沙量对比omparison of computed sediment concentration and field data at station No.1 in Oujiang Estuary(middle tide)

图5 瓯江2号站位(中潮)计算与实测含沙量对比omparison of computed sediment concentration and field data at station No.2 in Oujiang Estuary(middle tide)

4 结 语

根据Einstein和Chien的泥沙试验资料，采用最小二乘法拟合出新的掺混长度经验公式，在此基础上推导得到新的悬沙垂线分布公式，将此公式与2010年瓯江口各层含沙量实测资料进行对比，结果表明新公式能够较好地反映悬沙垂线分布规律。

［1］倪晋仁，遇惠甲.悬移质浓度垂线分布的各种理论及其间关系［J］.水利水运科学研究，1988(1):83-95.(NI Jinren，YU Huijia.The theory and its relationship of vertical distribution of concentration［J］.Hydro-Science and Engineering，1988(1):83-95.(in Chinese))

［2］钱宁，万兆惠.泥沙运动力学［M］.北京:科学出版社，1986.

［3］张红武.黄河下游洪水模型相似率的研究［D］.北京:清华大学，1995.

［4］严冰，张庆河.基于有限掺混长度概念的悬沙浓度垂线分布研究［J］.泥沙研究，2008(1):9-16.(YAN Bing，ZHANG Qinghe.Distribution of vertical suspended sediment concentration based on the finite mixing length conception［J］.Journal of Sediment Research，2008(1):9-16.(in Chinese))

［5］JUNG K T，JIN JY，KANG H W，et al.LEE Ho Jin.An analytical solution for the local suspended sediment concentration profile in tidal sea region［J］.Estuarine，Coastal and Shelf Science，2004，61(4):657-667.

［6］BUDIANTO O，MANO A.A turbulent and suspended sediment transport model for plunging breakers［J］.Coastal Engineering Journal，2008，50(3):349-367.

［7］傅旭东，王光谦.细颗粒悬沙浓度分布的影响因素分析［J］.水动力学研究与进展，2004，19(2):231-239.(FU Xudong，WANG Guangqian.Analysis on the factors affecting the vertical concentration distribution of fine sediment［J］.Journal of Hydrodynamics，2004，19(2):231-239.(in Chinese))

［8］VANRJIN L C.Sediment transport，partⅡ:suspended load transport［J］.Journal of Hydraulic Engineering，1984，110(11):1613-1641.

［9］吴剑，岳红艳，廖小永.悬移质含沙量沿垂线分布的探讨［J］.人民黄河，1998，20(4):4-5.(WU Jian，YUE Hongyan，LIAO Xiaoyong.Study on vertical distribution of concentration of suspended load［J］.Yellow River，1998，20(4):4-5.(in Chinese))

［10］陈永宽.悬移质含沙量沿垂线的分布［J］.泥沙研究，1984(1):31-39.(CHEN Yongkuan.Vertical distribution of suspended sediment in open channel［J］.Journal of Sediment Research，1984(1):31-39.(in Chinese))

［11］刘建军.明渠水流含沙量沿垂线分布研究［J］.泥沙研究，1996(2):105-108.(LIU Jianjun.Study on vertical distribution of concentration in open channel［J］.Journal of Sediment Research，1996(2):105-108.(in Chinese))

［12］McANALLY W H，MEHTA A J.Significance of aggregation of fine sediment particles in their deposition［J］.Estuarine，Coastal and Shelf Science，2002(4):643-653.