斐波那契数列与电路分析

张广华，于洲春

(国网技术学院电气工程系，山东济南250002)

斐波那契(Fibonacci)数列是数学史上一个著名的数列，又称“兔子数列”。1228年，文献［1] 提出了一个著名而有趣的关于兔子数量的问题，得到如下一串数:1、1、2、3、5、8、13、21、34、55、89、144……，这串数里隐含着一个规律:从第3个数起，后面的每个数都是它前面那两个数的和。

我们用数列{Fn}表示这串数，它便是斐波那契数列，具有非常简单的递推关系:

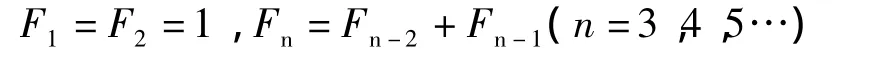
该数列是从兔子问题中抽象出来的，如果没有其它方面的应用，它就不会有强大的生命力。事实是，斐波那契数列确实在许多问题中出现，例如植物的生长、种子的排列和花瓣的数目等。而且，在数学、物理和化学等领域，斐波纳契数列也都有许多应用。可以说，斐波那契数列以他的兔子数列问题揭示了大自然某些规律。

斐波纳契数列有许多奇特的的性质，本文先列举两条与本文有关的内容。然后，介绍斐波那契数列在电路分析中的应用。

1 斐波纳契数列的特性

1.1 与黄金分割率的关系

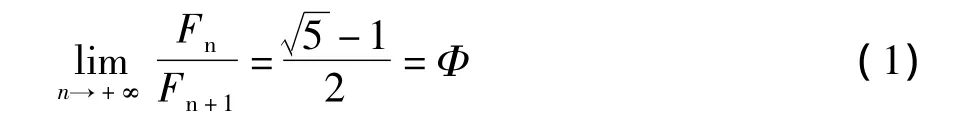
因此斐波纳契数列，又称黄金分割数列。斐波那契数列使我们对黄金分割的认识从静态走向动态。这里用Φ表示黄金分割率。

斐波那契数列{Fn}中每相邻两项的比值也构成一新的数列，我们用{Un}表示:

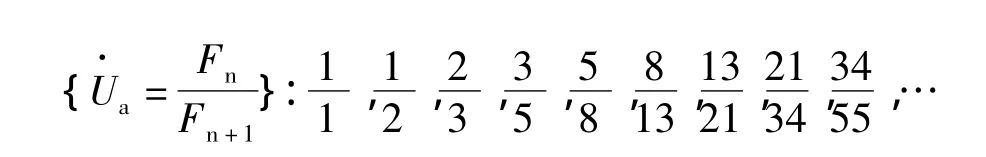
可以验证:数列{Un}中相邻两项分布于Φ的两侧，且奇数项大于Φ，偶数项小于Φ，但数列{Un}的极限为Φ。

由{Un}奇数项构成的数列为

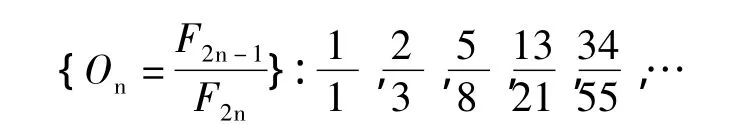
数列{On}是一单调递减数列，但各项均大于Φ，其极限为Φ，即数列{On}从大于Φ的方向趋近于Φ。

而由{Un}偶数项构成的数列为

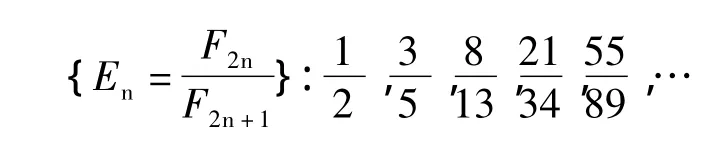
数列{En}是一单调递增数列，各项均小于Φ，其极限也为Φ，即数列{En}从小于Φ的方向趋近于Φ。

这样我们可以得到斐波那契数列{Fn}的三个派生数列:{Un}，{On}，{En}。

1.2 与矩阵的关系

易用数学归纳法证明(补充定义:F0=0)

两边取行列式，可得斐波那契数列的邻项公式

即斐波那契数列奇数项的平方比前后项的乘积大1，偶数项的平方比前后项的乘积小1。若仅考虑偶数项的情况，有

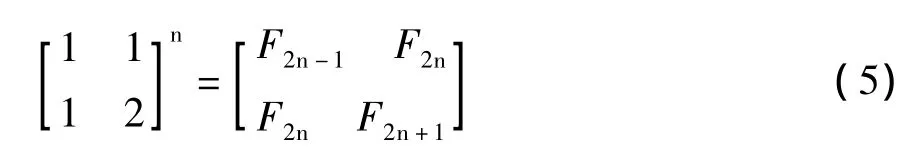
两边取行列式，同样可得式(4)。其实式(5)就是式(2)仅考虑偶数的情况。

这里我们得到斐波那契数列{Fn}的两个特性矩阵，二者分别对应式(2)和式(5)。

2 多级梯形网络的等效电阻

2.1 多级梯形网络的入端电阻

图1(a)所示电路可称为Γ型电路。图1(b)、(c)和(d)电路可看做由2节、3节及n节Γ型电路构成。我们称图1(d)所示电路为链型电路或梯形网络。

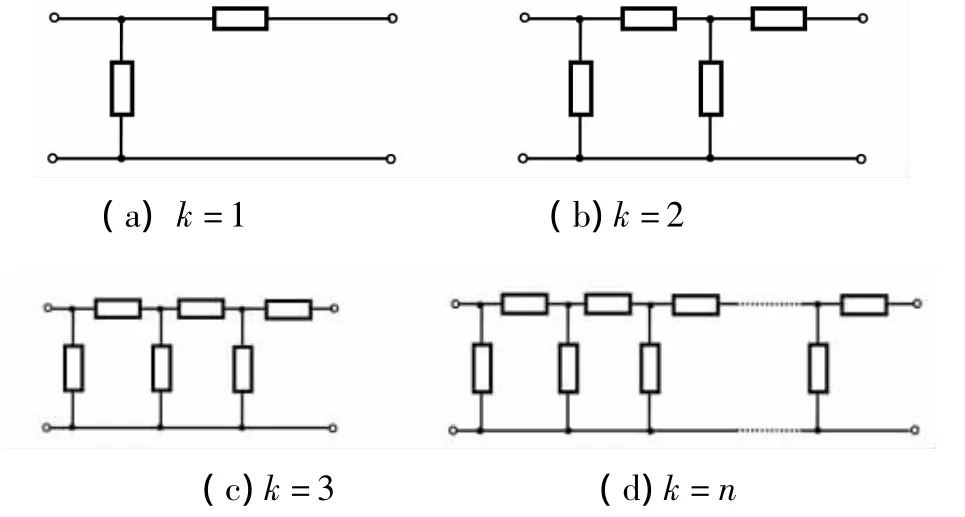
图1 多级梯形网络(多节Γ型电路)

若各电阻均为1Ω，下面我们来计算此类电路从始端看进去的等效电阻(又称为入端电阻)［4]。

我们很容易计算图1(a)、(b)和(c)所示1、2和3节Γ型电路的入端电阻:

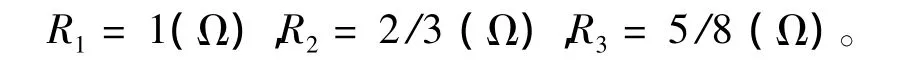
我们对比斐波那契数列{Fn}，发现:R1=F1/F2(Ω)，R2=F3/F4(Ω)，R3=F5/F6(Ω)，可推知

我们用归纳法证明上述推断:k=1时，R1=F1/F2显然成立。假设k=n－1时，表达式也成立，即Rn－1=F2(n－1)－1/F2(n－1)=F2n－3/2n－1。则须证明k=n时的表达式也应成立。现证明如下。

图1(d)所示n节Γ型电路，可重画如图2。

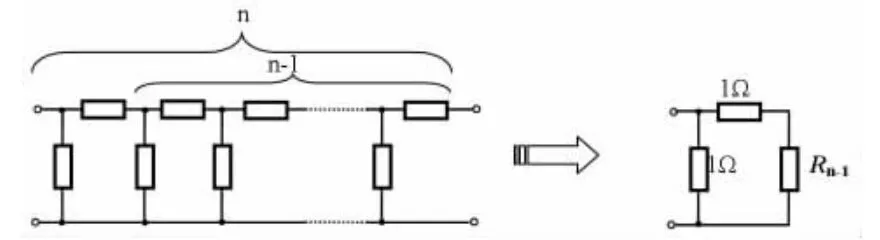
图2 n节Γ型电路的入端电阻

我们注意斐波那契数列{Fn}的递推特性:Fn=Fn－2+Fn－1，根据图2右侧的电阻并联关系得到

由上式推断可得结论:图1所示梯形网络的等效电阻Rn(n=1，2，3…)构成的数列{Rn}就是斐波那契数列{Fn}的派生数列{On}。

则无限多级梯形网络电路的入端电阻为

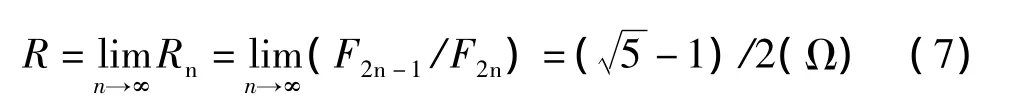
2.2 电路的一般分析方法

如图3所示的无限多级梯形网络，若入端电阻存在，不妨设为R，而去掉前面第一节后，其入端电阻不变，仍为R。

图3 无限多级梯形网络的等效电阻的求解

因此有R=［1/1+1/(1+R)]－1，可解得R=－1)/2(Ω)。

对比上述两种解法:应用斐波那契数列的性质和极限的思想分析此类电路，突出了动态的渐进过程，对理解结果和结论很有帮助。常规分析方法虽然看起来简洁清晰，但结果的得出略显晦涩，不便于我们理解和分析结论。

通过对比两种算法，我们也实现了从电路角度验证斐波那契数列{Fn}的重要特性:即斐波那契数列与黄金分割的关系，即式(1)。

3 多级梯形网络分析

3.1 二端口网络的传输参数方程

图4所示为无源二端口网络，其传输参数方程为［5]

我们将其改写成矩阵形式:

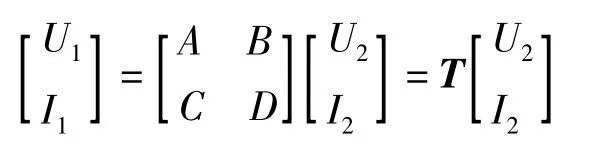
其中传输参数矩阵:

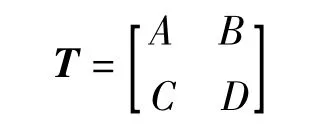
重画图1(a)所示电路，如图5所示。其传输参数方程为

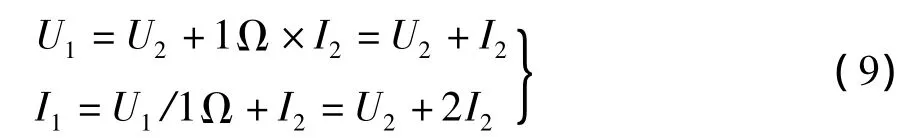
写成矩阵形式:

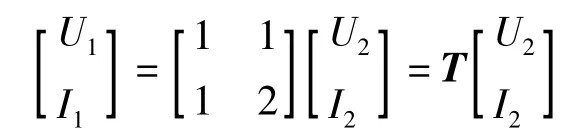
即图1(a)所示一节Γ型电路传输参数矩阵为

对比式(5)，矩阵T即为斐波那契数列{Fn}的特性矩阵。

图4 二端口网络

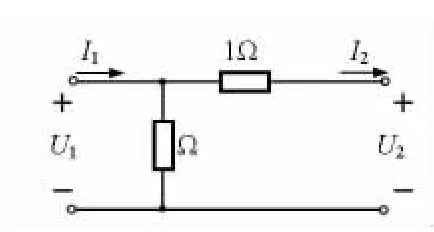
图5 二端口网络T参数计算

而图1(b)和图1(c)所示由2节和3节Γ型电路组成的级联网络。由电路理论分析可得，传输参数矩阵分别为

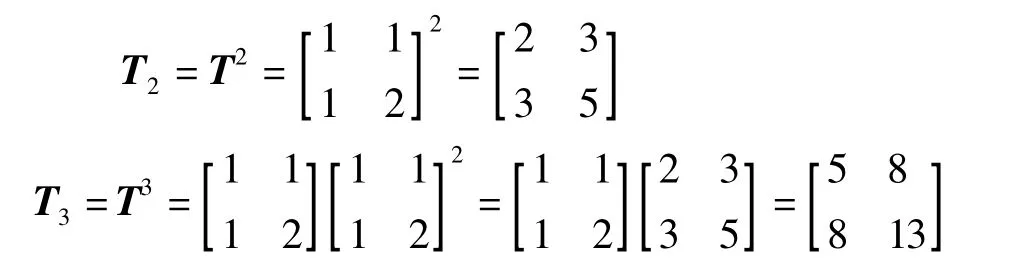
对比斐波那契数列{Fn}，我们发现

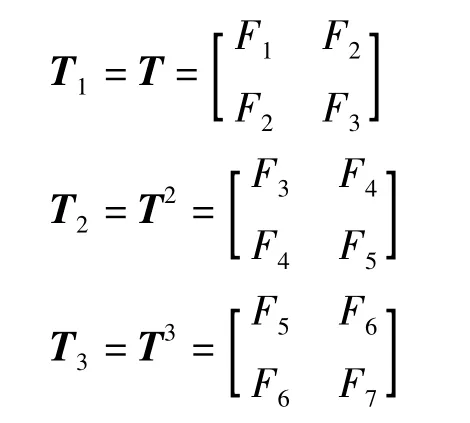
则对于图1(d)，由n节Γ型电路组成的级联网络，其传输参数矩阵为

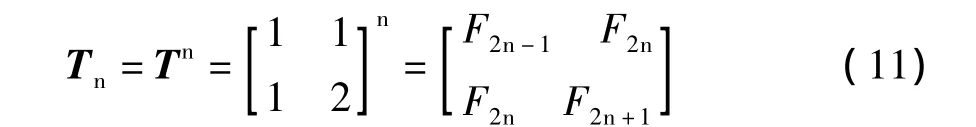
式中，T的下标1、2、3…n，表示1节、2节、3节…n节Γ型电路。

对比式(5)，斐波那契数列{Fn}的特性矩阵式(10)就有了其电路含义。此矩阵为图1(a)所示一节Γ型电路的传输参数矩阵T，而Tn即为图1(d)所示n节Γ型电路级联网络的传输参数矩阵。而斐波那契数列{Fn}与矩阵的关系(式5)，这样一个纯数学的公式也就具有了电路意义，我们可以从电路角度验证和解释这个公式。

图1所示电路为互易电路，根据电路理论，其传输参数满足:AD－BC=1［5]，而斐波那契数列恰好具有F2n－1F2n+1－=1如式(4)所示。

3.2 多级梯形网络的入端电阻

二端口网络输出接任意负载RL，如图6所示，其入端电阻为

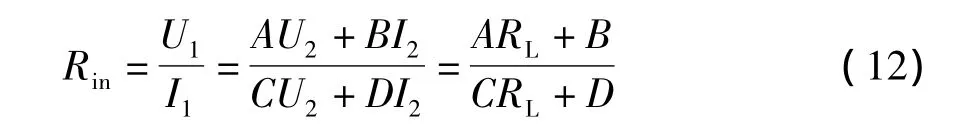
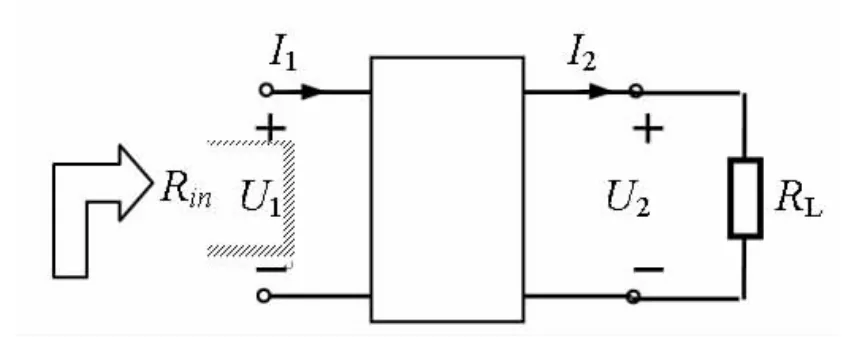
图6 二端口网络的入端电阻

特殊地情况下，若输出端开路，入端电阻:Rin(oc)=A/C;若输出端短路，入端电阻:Rin(sc)=B/D。

对于图1(d)所示n节Γ型电路，可以得到如下结果:

(1)输出端开路，入端电阻:Rin(oc)·n=A/C=F 2n－1/F2n，即:

Rin(oc)1=F1/F2=1(Ω)，Rin(oc)2=F3/F4=2/3(Ω)，Rin(oc)3=F5/F6=5/8(Ω)，…

可见:数列{Rin(oc)n}就是斐波那契数列{Fn}的派生数列{On}，这也与前面的结论一致。

(2)输出端短路，入端电阻:Rin(sc)n=B/D=F2n/F2n+1，即:

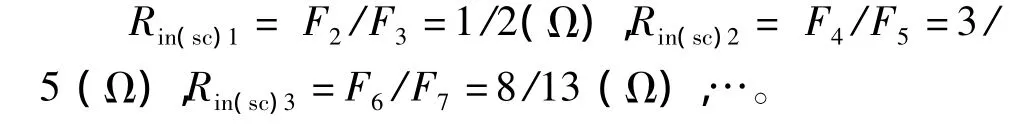
数列{Rin(sc)·n}就是斐波那契数列{Fn}的派生数列{En}，其极限也为Φ。

3.3 结论

图1所示n节Γ型电路(n=1，2，3…)，输出开路时，入端电阻构成的数列即为斐波那契数列{Fn}的派生数列{On};输出短路时，入端电阻构成的数列即为斐波那契数列{Fn}的派生数列{En}，这样斐波那契数列{Fn}的派生数列{On}和{En}便都具有了电路意义。

{On}和{En}的极限都为Φ，也即图3所示无限多级梯形网络(n=∞)，无论输出开路或是短路，其入端电阻是一样的，都等于Φ，这是很令人惊奇的。其实，更进一步分析，无论输出接任何负载，入端电阻也不变，等于Φ。下面给出证明:

图1(d)所示n级梯形网络，接任意负载RL时的入端电阻为:

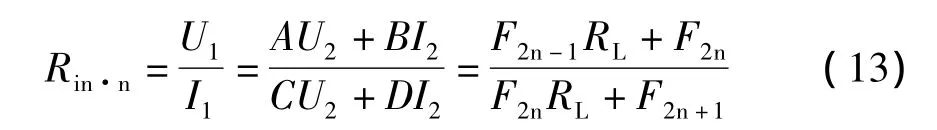
取极限，则得到无限多级梯形网络接任意负载RL时的入端电阻为

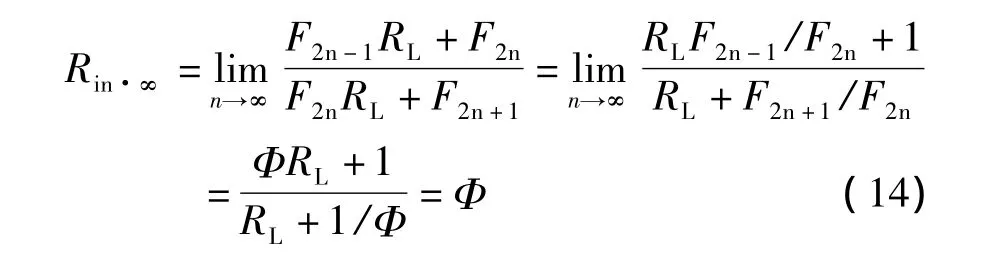
4 结语

本文给出了斐波那契数列与特定矩阵T的关系，研究了斐波那契数列的两个派生数列{On}和{En}，进而从电路角度分析验证斐波那契数列的相关特性，并应用斐波那契数列的性质和极限思想完成特定电路分析和计算。

［1] 莱昂纳多·斐波那契(Leonardo Fibonacci)·算盘书［M] (Liber Abaci)，1228

［2] 吴振奎·斐波那契数列欣赏［M] ·哈尔滨:哈尔滨工业大学出版社，2012

［3] 康士凯·斐波那契数列［M] ·上海:上海科技教育出版社，1992.05

［4] 郑金·斐波那契电路［J] ·北京:数理天地(高中版)，2009.9

［5] 江辑光·电路原理［M] ·北京:清华大学出版社，1996