基于NSGA－Ⅱ算法的多目标无功优化

孙银锋，闫 旭，李泽财

(1．东北电力大学电气工程学院，吉林吉林132012;2．北京航空航天大学自动化与电气工程学院，北京100191;3．华能铜川电厂，陕西铜川727100)

随着电力系统运行水平的提高，无功优化已不再是单纯考虑网损最小的单目标优化问题，而是逐渐发展成一个综合考虑各运行指标的多目标优化问题［1］。无功优化可以优化电网的无功潮流分布，并降低电网网损和电压损耗，从而改善电压质量，同时保正用电设备安全可靠运行。传统优化方法将各优化目标设置不同的权重［2］，通过权重的调整得到pareto最优值，亦可将部分优化目标视为约束条件，最终实现多目标问题向单目标问题的转化。然而这样做一方面增加了主观因素，另一方面每次也仅能得到一个解。因此，本文引入了NSGA－Ⅱ算法［3］，采用有效的精英策略，解集以成组形式逼近pareto域，具有较低的计算复杂度，并无需指定共享半径。将NSGA－Ⅱ算法应用于无功优化问题的求解过程，建立了以补偿设备投资成本和网损最小为优化子目标的优化模型。

1 无功优化的多目标优化模型

电力系统无功优化多目标问题优化模型为

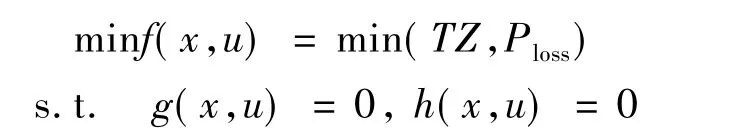
式中:u为控制变量(包括发电机有功、无功输出功率、发电机机端电压和变压器变比等);x为状态变量(如节点电压幅值和相角);f(x，u)为标量目标函数，常为发电费用或网损;TZ为补偿设备投资成本;Ploss表示网损;g(x，u)是潮流方程等式约束;h(x，u)是不等式约束，分为变量不等式和函数不等式，常为系统的安全约束和元件的运行限值约束［4］。

有功网损最小化的目标函数为

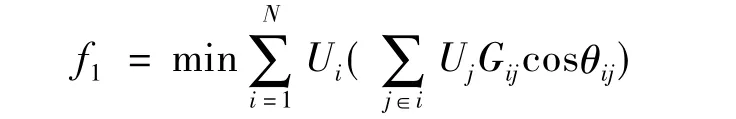
式中:N为所有线路支路的集合;Gij为系统节点导纳矩阵的实部;Ui，Uj分别为节点 i，j的电压; θij是节点i，j的相角差值。

以无功补偿投资最优的目标函数为

式中:Ns为补偿装置的补偿点集;Ci为补偿节点i的安装费用;Cv为补偿装置单位容量的运行费用(万元/a·MVar);Qci为补偿节点i的补偿容量。

约束条件包括等式约束和不等式约束，等式约束即满足潮流方程

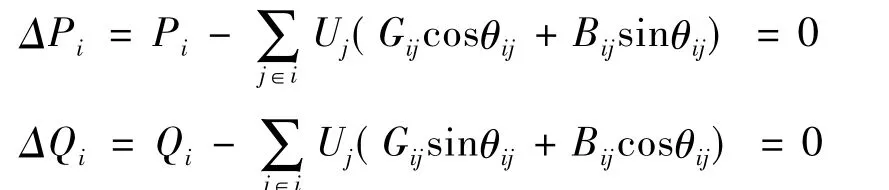
不等式约束考虑:PV节点的电压，有载调压变压器的档位，无功补偿装置的组数等控制变量上下限;PQ节点的电压幅值，PV节点无功注入，支路电流幅值等状态变量上下限。

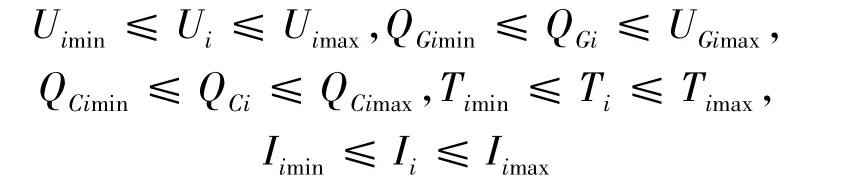
式中:QCimax、QCimin分别表示第i无功补偿器的无功补偿容量上下限;Uimax、Uimin分别表示节点i电压幅值上下限;Iimax、Iimin分别表示第i条支路的电流上下限;Timax、Timin表示第i台有载调压变压器分接头档位的调节上下限。

2 NSGA－Ⅱ算法实现

NSGA－Ⅱ算法由于利用非支配排序，提高了收敛速度，对拥挤距离的定义避免了选择共享参数的困难，同时为了扩大采样空间引入了精英策略的保优机制［5］。

2．1 编码设计

根据无功优化问题的特点，采用实数编码，所有无功补偿装置的位置和容量皆由十进制整数求出，而补偿装置的配置范围是0－最大节点号。

2．2 初始群体生成

初始化规模为N的群体每个无功补偿点的位置和容量。

2．3 快速非支配排序

计算前，要先根据无功优化的多目标模型进行潮流解算，得到个体的目标函数值，依据个体的非支配水平进行种群分层排序。

2．4 计算拥挤距离

拥挤距离的概念是为了防止个体局部堆积从而保持个体多样性而提出的。根据快速非支配排序结果，对一层中的pareto解利用无功优化中目标函数值计算拥挤距离。目标空间第i点的拥挤距离等于它与同一等级相邻点i－1和i+1组成的矩形的两个边长之和。这一方法可自动调整小生境，使得计算结果在目标空间均匀散布，鲁棒性较好［6］。个体i的拥挤距离D［i］表示为

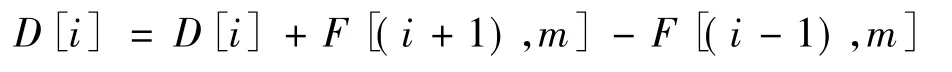
其中，F［i，m］表示个体i的第m个目标函数值。

2．5 选择、交叉和变异算子

选择算子的作用是为了防止有效基因的损失，使高性能的个体得到更大的生存概率，可以提高全局收敛性和计算效率。选择算子采用精英策略与轮赛制选择相结合的方法。轮赛制选择是随机选2个个体，若非劣解等级不同，则取等级高(级数小)的个体。否则，如果两点在同一等级上，则取比较稀疏区域内的点，可使进化向非劣解和均匀散布的方向进行。

精英策略即保留父代中优良的个体直接进入子代，它也是遗传算法以概率1收敛的必要条件。具体方法是:将父代和子代全部个体合为统一的种群，并放入进化池中，种群的个体数变为2N;按非劣解等级分类，计算每一个个体局部拥挤距离，依等级逐一选取个体，直至个体总数达到N;形成新一轮进化的父代种群(个体数为N)，同时开始新一轮的选择、交叉和变异，形成新的子代种群［7］。

交叉算子对上行附加码采用部分匹配交叉策略，而下行变量码不动，即交叉过程中只对选址单元编号在附加码中的排列顺序进行调整，即相应地改变了1型基因的分布。

变异操作采用倒位遗传算子。从父个体随机选择两个变异点，两点间的上行附加码按反序重新排列，而下行的变量码顺序不变。

2．6 适应度计算

首先，解码染色体;然后按优化模型计算每个个体相应的目标函数，再依据目标函数值进行非劣分层，计算每层个体虚拟适应度。

1)对同层的个体距离初始化，令L［i］=0。

2)对同层的个体按第m个目标函数值进行升序排列，令 L=sort(L，m)。

3)使排序边缘上的个体拥有选择优势，给定一个较大数 L［1］=L［N］=M 。

4)计算排序中间的个体拥挤距离为

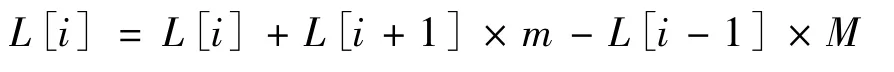
式中，L［i］×m为第i个体的第m目标函数。

5)对不同的目标函数，重复操作步骤2)～4)。

3 算例分析

本文以IEEE39节点系统为例，对无功补偿装置(电容器/电抗器)的位置和容量［8］进行优化配置计算。该系统包含10台发电机，12台可调变压器，34条线路，19个负荷点，基准容量为100 MW，发电机母线电压为20 kV，可调变压器变比上下限为1.05 和0．95，发电机电压上下限为 1．1 和 0．9，设无功补偿设备补偿点为4个。

NSGA－Ⅱ计算过程中所需参数设置:种群规模取为300，最大迭代次数为200，交叉率设为0．9，变异率取0．1。经过仿真计算，从pareto最优解空间中抽取几个典型的解示于图1中，从左至右依次将这些解编号为1－8。

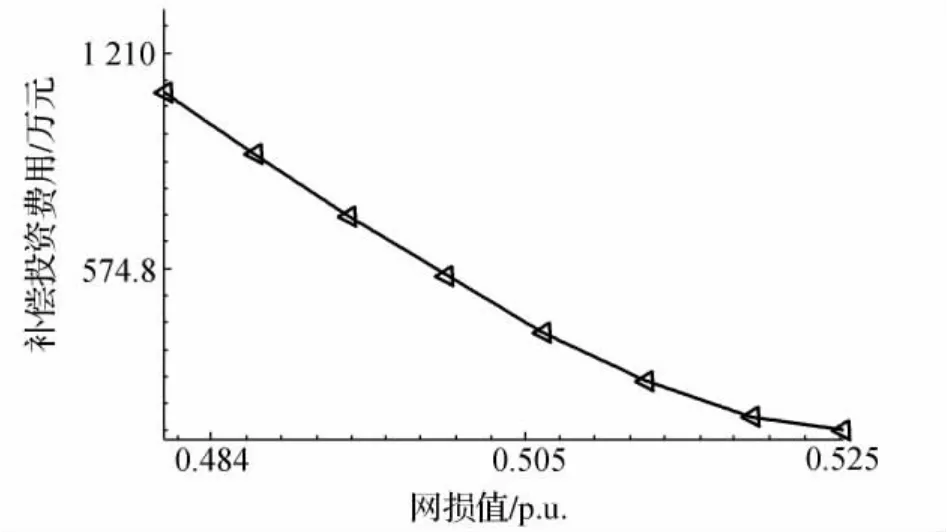
图1 优化得到的几个典型最优解

从图1可以看出，解1的网损最小，但是补偿设备投资却很大，而解8投资最省但网损非常大。因此尚需对优化解进行比较分析，具体的结果见表1。

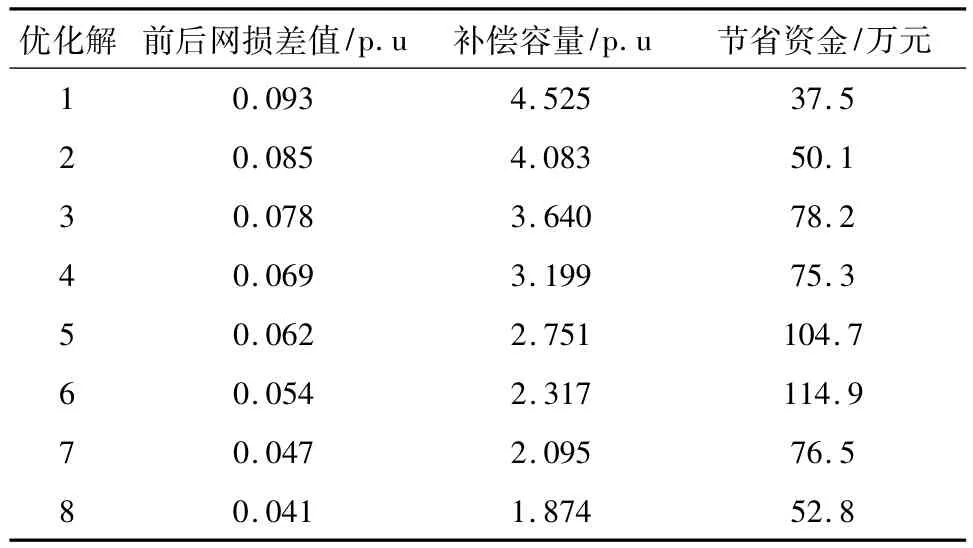
表1 优化解的进一步比较

由表1可得解6的补偿效果最好，获得了最大的经济效益，因此为所要求的全局最优解，而此时的最优补偿地点为节点20、24、9和7。

优化前后各节点电压变化情况如图2所示。显然优化后的各母线电压也均有不同程度的提高。

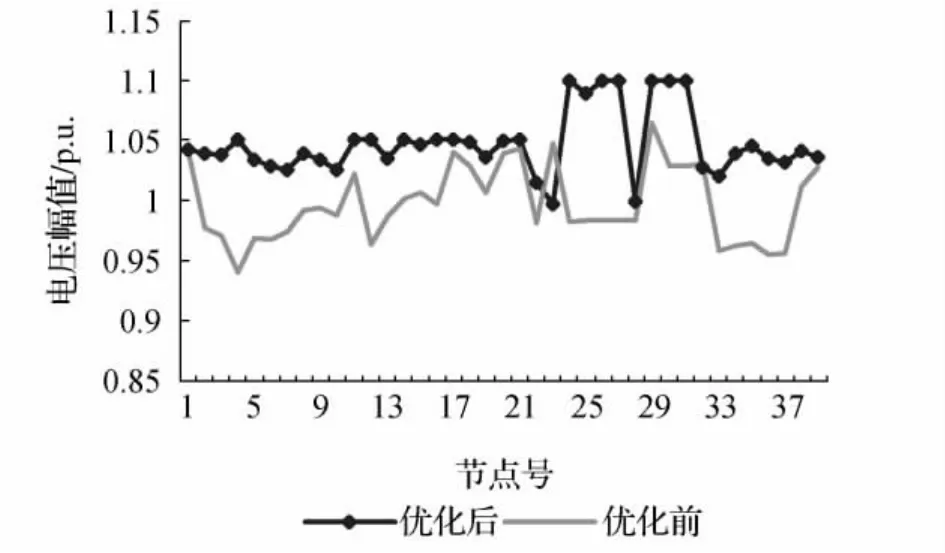
图2 优化前后系统各节点电压变化

4 结束语

本文应用NSGA－Ⅱ算法针对IEEE－39节点系统，通过编码、快速非支配排序、交叉、排序和变异等步骤实现了多目标函数的无功优化仿真计算。结果表明，此方法能够真实地反映实际物理过程，并可以很好地协调网损和无功补偿设备的投资费用这两个优化目标。经过优化解空间的精选可以很方便找到协调多目标函数的全局最优解。

［1］李智欢，段献忠．多目标进化算法求解无功优化问题的对比分析［J］．中国电机工程学报，2010，30(10):57 －65．

［2］张杰，周硕．运筹学模型与实验［M］．北京:中国电力出版社，2007．

［3］DEB K，PRATAP A，AGARWAL S，etal．A fast and elitist multiobjective genetic algorithm:NSGA－Ⅱ［J］．IEEE Transactions on Evolutionary Computation，2002，6(2):182 －197．

［4］王向臣，徐宏全，于长永等．电网无功补偿实用技术［M］．北京:中国水利水电出版社，2009．

［5］赵国波，刘天琪，王春明等．基于NSGA－Ⅱ算法的分布式电源优化配置［J］．现代电力，2012，29(1):1 －5．

［6］张成芬，赵彦珍，陈锋，等．基于改进NSGA－Ⅱ算法的干式空心电抗器多目标优化设计［J］．中国电机工程学报，2010，30(18):115－121．

［7］包伟，姚建刚，李晴，等．GIS支持下基于NSGA－Ⅱ算法的火电厂多目标选址［J］．电力系统保护与控制，2008，36(22):25－28．

［8］刘传铨，张焰．电力系统无功补偿点及其补偿容量的确定［J］．电网技术．2007，31(12):78 －81．