变压器直流偏磁对交流励磁的影响

史海涛，潘 超

(东北电力大学输变电技术学院，吉林吉林132012)

通过电路等效参数计算获得。

棱边单元插值函数为

高压直流输电(HVDC)、地磁感应电流(GIC)中变压器的直流偏磁计算与分析是备受重视的前沿课题。变压器电磁场计算通常采用有限元法直接在时域求解场域方程，计算量大，效率低［1］。文献［2］采用T法建立变压器三维模型，分析其突发短路，但T法求解多连通问题困难，文中只针对单连通模型进行分析，未考虑变压器的整体磁路。由于T－φ法处理多连通问题难度较大，目前大都采用A－V法计算变压器磁场［3］。本文基于棱边有限元方法建立变压器三维磁场模型，分析直流偏磁时原、副边电流的变化和对应关系。通过与实验对比，讨论不同直流注入方式下变压器的直流偏磁效果，并归纳其变化规律。

1 变压器直流注入方式及仿真模型

变压器直流偏磁实验有两种实验方式:方式1为交流、直流电源处于变压器两侧;方式2为交流、直流电源处于变压器的同侧，如图1所示。

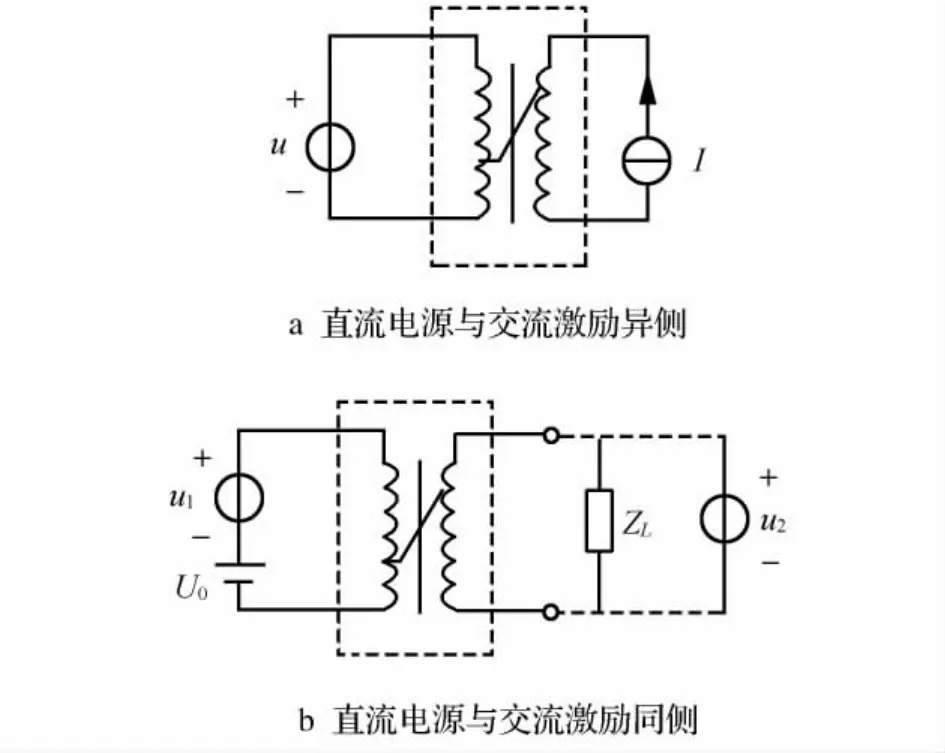
图1 不同的直流注入方式

三维棱边有限元法采用矢量磁位A，根据Maxwell得到非线性磁场方程为

式中:μ为导磁材料的磁导率;J为电流密度，需要

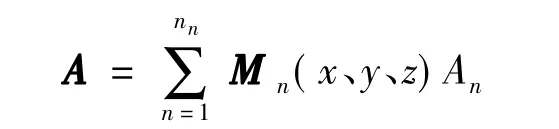
式中:{Mn，n=1，2，…，nn}为基函数序列，由相关单元形状函数Nl对应叠加形成;n为基函数序列通项编号;nn为总项数(总棱边数)。

应用格林定理，得伽辽金加权余量方程为

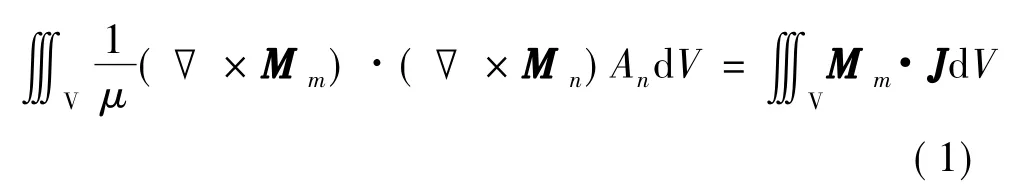
通过电路等效参数计算获得。

棱边单元插值函数为

式中{Mm}为基函数序列，且权函数与基函数相同。若已知电流i，将权函数代入方程(1)，针对全部权函数，将加权余量方程离散形成代数方程组，求解可得所有节点或棱边上的A，进而计算其他场量，如B和H等。

2 实验平台

实际实验平台如图2所示，实验变压器型号为BK500，参数如表1所示，两种直流注入方式对应的实验接线如图3所示。

图2 变压器直流偏磁实验平台

3 结果分析

利用三维有限元模型，对不同注入方式下变压器的直流偏磁进行实验和仿真。变压器负载运行，副边接220 V/40 W的灯具，无直流注入时，原、副边电流的计算结果和实验结果对比如图4所示。

图4中i1、i2为原、副边电流;ie为励磁电流，且ie=(n1i1－ n2i2)/n1，n1、n2为匝数。不难看出，无直流时仿真结果与实验测量数据基本一致，说明了仿真计算的正确性和有效性。

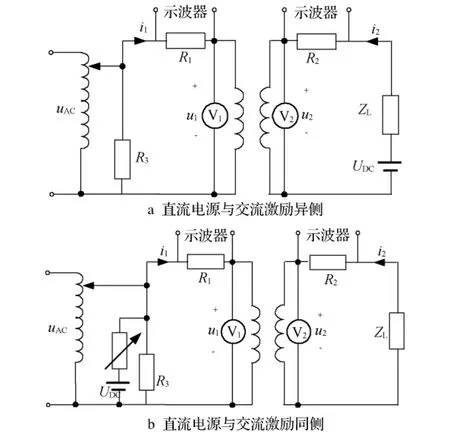
图3 不同直流注入方式的实验接线图

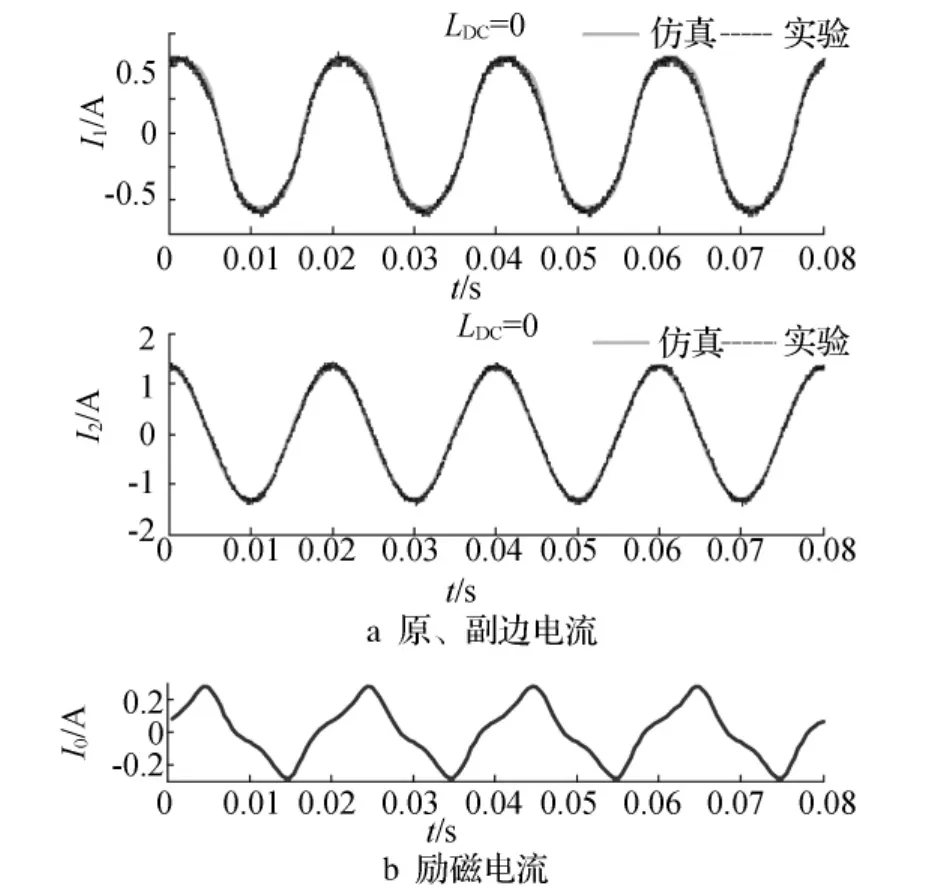
图4 负载运行无直流时的原、副边电流

方式1:副边接12 V直流电压源时，直流电流折算至原边约为50%I0，I0为变压器空载电流实测值(见表1)。此时，原、副边电流的计算结果和实验结果对比如图5所示。

方式2:原边接12 V直流电压源，直流电流约为50%I0。此时，原、副边电流的计算结果和实验结果对比如图6所示。

表1 实验变压器参数

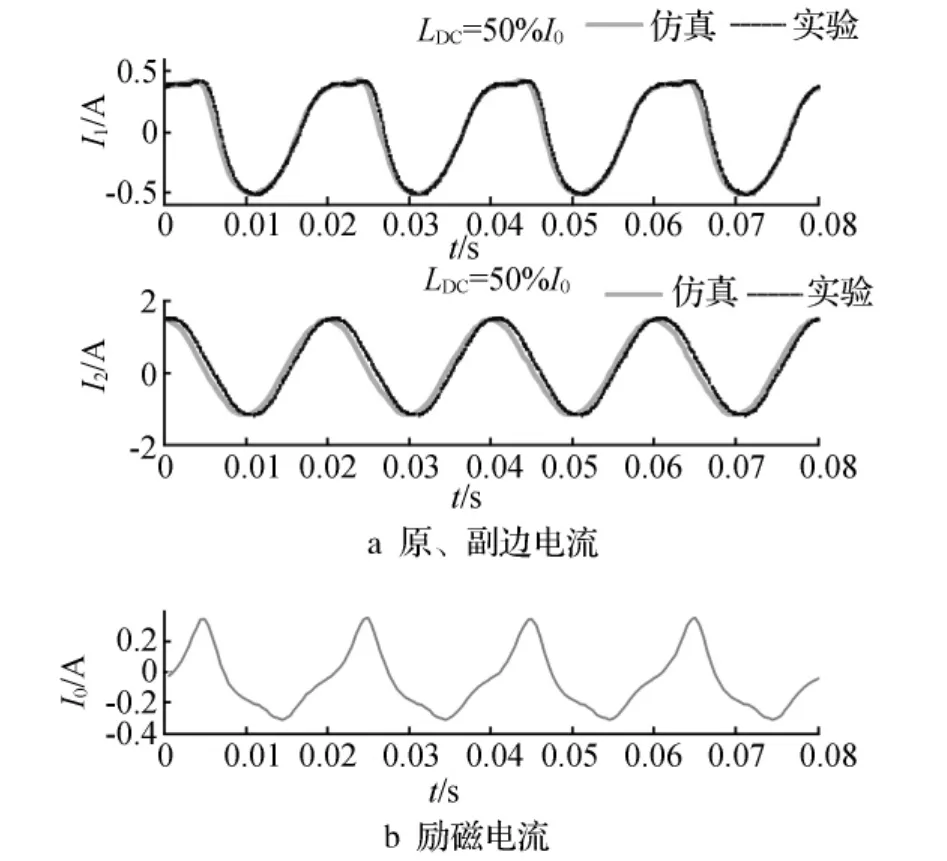
图5 IDC=50%I0时方式1的原、副边电流

从图5、图6中可以看到，变压器发生直流偏磁时，铁心励磁饱和程度加深，励磁电流增大，原边电流发生明显畸变，副边电流只受副边绕组注入直流大小的影响而整体变化，不同直流注入方式下变压器交流的励磁变化情况相同。

4 结论

1)利用三维有限元方法计算变压器直流偏磁，可以反映出变压器电流在直流扰动下的变化规律。负载运行直流偏磁的电流计算结果与实验结果基本相同，验证了该方法的正确性。

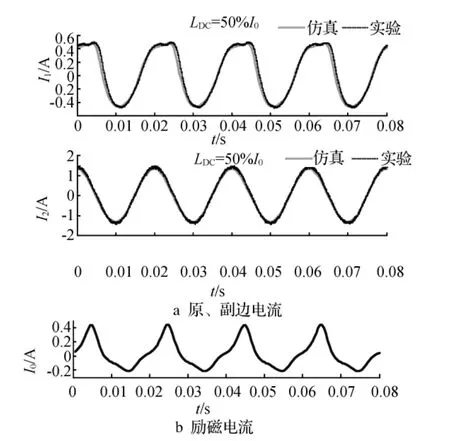
图6 IDC=50%I0时方式2的原、副边电流

2)直流电流在原边或副边注入都能有效模拟变压器在直流偏磁时的饱和励磁情况，两种注入方式下的交流电流计算结果基本相同。

［1］程志光，高桥则雄，博扎尼·弗甘尼，等．电气工程电磁热场模拟与应用［M］．北京:科学出版社，2009．

［2］梁振光，唐任远．三相电力变压器的场路耦合模型及突发短路过程计算［J］．电工技术学报，2004，19(3):46 －51．

［3］张秀敏，苑津莎，崔翔．用棱边法与节点有限元耦合的E－E－ψ法计算三维涡流场［J］．中国电机工程学报，2003，23(5):70 －74．