一种考虑系统内损的竞争性设施选址模型和方法

李 佳， 徐福缘， 叶 佳

（上海理工大学 管理学院，上海 200093）

传统竞争性设施选址问题的研究重点只局限于新建设施，为了克服这一局限性，本文将竞争性设施选址问题的研究对象拓展到系统的层面.首先引用供需网系统［1］的相关理念，将竞争性设施理解为：在给定地区内已经存在提供同类产品和服务设施（包括系统内部的设施和系统外部的设施）的情况下，为了充分满足客户的需求，系统在该地区内建立的新设施.进而将系统解释为企业与企业之间的合作体，或者是企业与供应链，乃至供应链之间的合作体，强调了它们以合作为主——即尽量减少系统内竞争性内损，而不是只强调企业之间、供应链之间的竞争性为主.

现有的竞争性设施选址研究总结起来有以下几个特点：a.研究目标——以利润最大化为目标.很明显，在现有的研究中，利润最大化是研究的主要目标，这主要是考虑了来自供应链外的竞争.b.研究对象——以新建竞争性设施及其所在供应链为研究对象.c.研究侧重——侧重于研究供应链外部竞争性设施对供应链内部竞争性设施建设的影响.然而，从充分合作与共赢及减少恶性竞争的角度出发［2］，可以将优化的目标（范围）扩大化，即扩大到相关企业和供应链（可以不止一个供应链）内外的更大范围内.将这个范围作为一个系统，并对其所涉及的目标进行优化.因为当新的设施进入系统时，现有设施的市场份额可能会降低，这看似只是整个系统的市场份额在系统内各设施之间简单的转移现象，并无负面效应产生.但是，实际上将会对整个系统及系统内其它设施造成损失，本文把这种现象称为“系统内自损”.实际上，当系统内某设施的市场份额减少到某一程度时，其可能对于整个系统来说，不再具有盈利能力.这时，系统不得不关闭该设施或者减少其运营成本（包括裁员或者降低设施质量），而这些通常会对系统的形象产生影响，或者提升设施的质量（这就意味着产生更多的成本，而且系统内其它设施将会因此遭受自损）.以当前汽车销售的主要渠道——4s专卖模式为例进行说明：假设某汽车品牌在某市已有3家本品牌4s专卖店（供需网系统内部），5家同类品牌的4s专卖店（系统外部），为满足日益增长的客户需求，拟在某市新建一家该品牌4s专卖店，该新店的选址问题即为本文将要研究的内容.不同于其它研究的是，该研究旨在针对以下问题进行分析：由于新店的进入，系统内部各4s店之间的竞争加剧，市场份额遭受一定程度的流失，从而产生“系统内自损”；而各设施之间为了保持自己的市场份额，势必会采取一定的措施，从而带来一系列问题，如恶性竞争、窜货等渠道横向冲突行为，这些行为的产生更加剧了“系统内自损”的严重程度，从而对系统利益造成更大的损害.因此要优化竞争性设施选址问题，必须使“系统内自损”水平达到一定条件下的最小化.

综上所述，本文将竞争性设施选址问题中“系统内自损”最小化作为系统研究的目标，并建立相应的优化模型，力图使竞争性设施的选址达到某种意义上的最优.

1 模型的建立

1.1 研究假设及指标分析

现拟在某地区建立一新设施，假设在该地区已经存在同类设施数量为m，其中，前k（k≥1）个设施是系统内部设施（m＞k）.同时，假设有n个需求点，每个需求点的位置和购买力为已知量.现有设施的位置和质量也均为已知量.

本文将出现的所有符号意义如下：

x表示新设施的位置，x＝（x1，x2）；

n表示需求点的数量，已知量；

pi表示需求点的位置，pi＝（pi1，pi2），已知量；

qi表示需求点pi的购买力（需求）；

m表示现有设施的数量；

tj表示现有设施，j＝（1，…，m）；

k表示系统内现有设施的数量，k∈（0，m）；

d表示需求点和设施之间的距离；

dij表示需求点pi和现有设施tj之间的距离；

dix表示需求点pi和新建设施x的距离；

α表示设施对需求点的引力值；

αix表示新建设施x对需求点pi的引力值；

αij表示现有设施tj对需求点pi的引力值；

fi（·）表示描述距离对吸引力造成的阻力，是以距离为自变量的非负增函数；

ui（·）表示效用函数，其中ui（·）＝αλ1·（fi（·））－1；

uij表示需求点pi从现有设施获得的效用；

uix表示需求点pi从新建设施获得的效用；

X表示新建设施的备选设施节点集合；

R表示系统内竞争者已建立的设施集合；

Fl表示备选设施l的运营成本，l∈N，N为备选设施数量；

F表示服务设施的运营总费用；

xl表示为0，1变量，xl＝1表示备选设施l开放，否则xl＝0.

引力值主要指设施的商誉、规模、服务水平、商品质量等因素，可通过市场调查及模糊综合评价法等综合评定，设施对需求点引力值的大小对需求点客户的购买力去向具有重要的作用.

效用是影响客户选择的一项重要影响因子，简单地说就是客户从竞争性设施所提供的购物服务中感受到的满足程度.效用函数的概念最早是由Huff［3］针对零售店竞争性选址问题提出的.典型的效用函数形式为

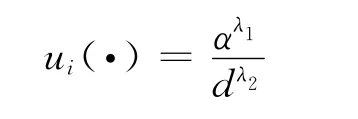
式中，λ1，λ2为已知参数表示距离产生的阻力.

为了避免效用函数的分母为0，Nakanishi［4］对该式进行了修正，其形式为

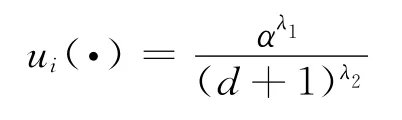
1.2 目标函数建立

基于以上假设，在“系统内自损”最小化为目标的前提下，本文得出，在新设施建立之前，系统内部现有设施所占的市场份额为

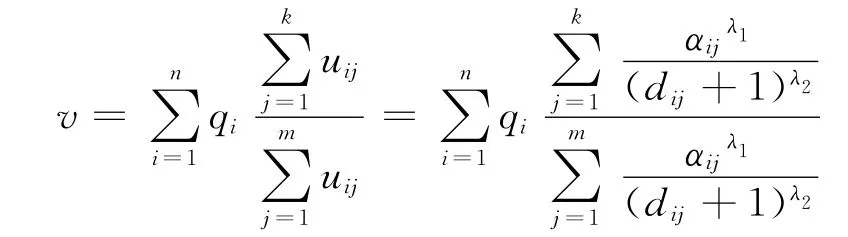
新设施建立之后现有设施所占的市场份额为

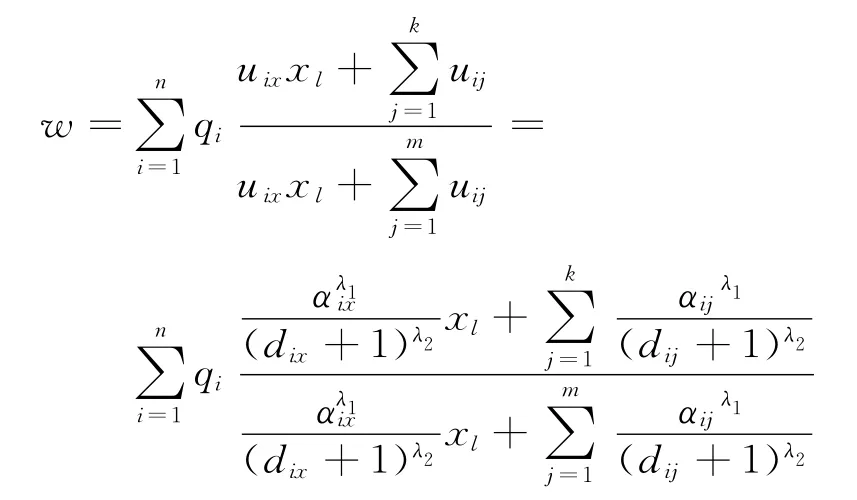
则有目标函数

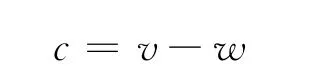
因此，目标应是新设施建设前后系统内自损最小，即

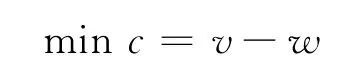
则目标函数最终形式为

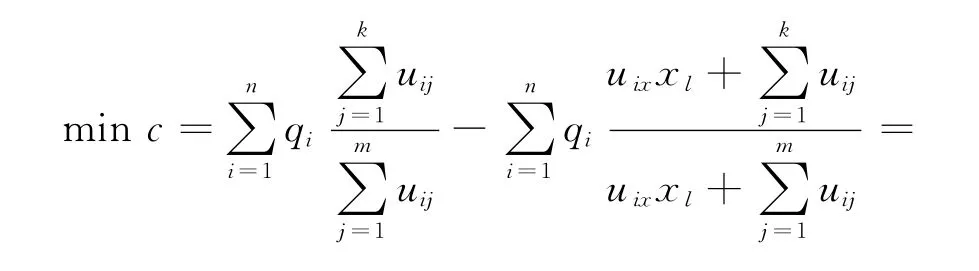
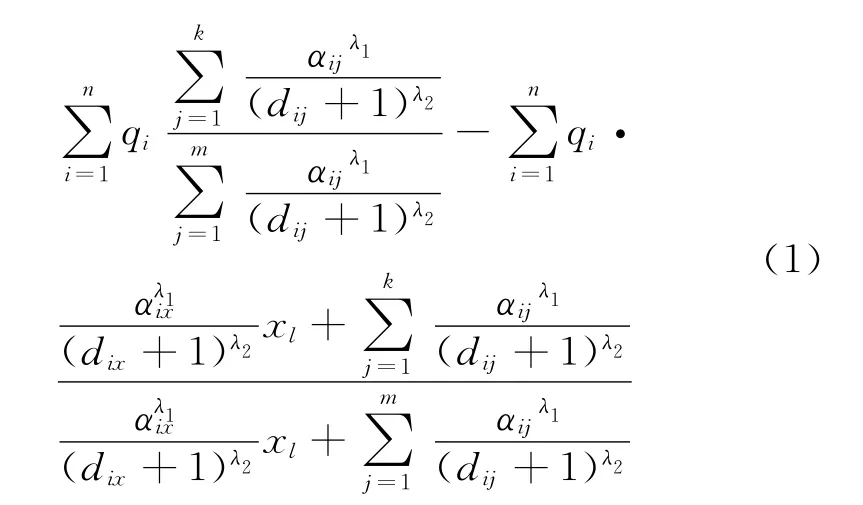
可以看出

1.3 模型建立

问题可描述为

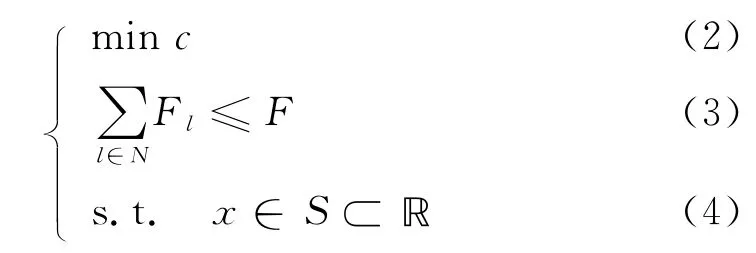
式中，S表示平面上新的竞争性设施拟选址的目标区域；R表示实数集.

2 分散搜索算法

2.1 算法基本思想

竞争性设施选址模型的求解过程较为复杂，一直以来都是个难题.针对设施选址模型的求解，现有的文献尝试并设计出了多种算法.文献［5－6］设计出线性逼近算法和分枝定界算法，这两类算法的优势在于求解中小规模的问题，但是对于大规模问题的求解却存在很大的局限.这种情况下，文献［7］首次提出了分散搜索算法，该算法是一种智能进化算法，与一般的智能算法有着显著的差异性.这种差异性主要体现在解的产生方式上.分散搜索算法不是按传统的方法随机给出解，而是不断地对具备较好性能的解进行组合、可行化处理以及局部改善等一系列操作，最终产生保留父代优良性能的解.文献［8］创新性地使用分散搜索算法解决了物流中心的选址问题，并取得了良好效果.文献［9］给出一种基于人工蚂蚁优化思想的新的求解方法，得到了满意效果.文献［10］运用蜂群算法，给出了一种新的求解方法，通过调整算法参数，得到了较好结果，并且验证了算法的可行性和有效性.本文拟利用分散搜索算法对模型（1）进行求解.

2.2 分散搜索算法步骤

分散搜索算法的基本步骤是：

a.由初始群产生一个具有差异化的参考集；

b.遵循一定的标准，从参考集中产生一个解集集合；

c.对由参考集产生的解集集合中的所有解集进行循环性的组合、可行化处理和局部改善，从而产生新的解；

d.将最终产生的新解加入初始种群产生的参考集，形成新的参考集（新参考集中的解既能够保留父代的优良性能，同时又能防止过早收敛）；

e.按照上述方法一直循环迭代至参考集中解的质量达到最优，即不能再被改善.

2.3 分散搜索算法实施策略

下面简要叙述模型的分散搜索算法实施策略.

a.初始参数：假设初始群的规模大小为2hmax，品质解的数量为o1，差异解的数量为o2，则参考集的规模为o，其中o＝o1＋o2.

b.初始群：随机产生一个向量集T0，使用一定的算法（如贪婪算法）对向量集中的各个向量进行可行化处理.

c.产生参考集：质量解和差异解构成参考集RS.参考集的产生过程如下：第一步，将向量集T0中的向量根据目标函数值的大小从大到小依次排列出来；第二步，将前o1个解加入参考集RS，这o1个解就被称为参考集RS的品质解；第三步，从T0－RS中挑选o2个有较大差异的解加入RS，这o2个解就被称为参考集中的差异解.

d.产生子集集合：第一步，根据目标函数值大小，在参考集RS中选取一个目标函数值最大的品质解，在剩余部分中选取任意两个解，将该品质解和这两个解组成不同子集，从而得到子集集合S1；第二步，在参考集RS中选取目标函数值最大的前两个解，在剩余部分中任意选取两个解，将它们组成不同子集，从而得到子集集合S2；第三步，令RV＝S1∪S2，即RV为新产生的子集集合.

e.线性组合产生新的可行解：对RV中的解进行线性组合，从而产生新的解V.

f.质量改善：局部改善新解V的质量.

g.更新参考集RS：每得到一个新的可行解V，则对参考集RS进行更新.

3 算例分析

假设网络中有20个节点，如表1所示，消费者所在节点为P1～P20.假定现有设施位于节点P1，P2，其中，P1为系统内节点，P2为系统外节点，引力参数分别为524和386.决策者的候选设施所在节点为P3～P20.决策者候选设施的吸引力参数如表2所示，消费者需求量分布如表3所示，设施各阶段的经营费用如表4所示.

F＝209，λ1＝λ2＝1，hmax＝50，o1＝3，o2＝2.Lingo软件和分散搜索算法的计算结果分别如表5～6所示（见下页）.

表1 各节点坐标Tab.1 Node coordinates

表2 各设施引力值Tab.2 Facilities gravity

表3 消费者的需求分布Tab.3 Consumer demand distribution

表4 设施运营费用Tab.4 Facilities operating costs

表5 Lingo软件计算结果Tab.5 Lingo results

表6 分散搜索算法计算结果Tab.6 Scatter search algorithm results

通过对表5和表6的比较可以看出，用分散搜索算法和Lingo优化软件求解的运行时间、最终得到的目标值及最优解基本一致，但是Lingo优化软件的求解时间是分散搜索算法所用时间的1 019.09倍.

4 结 论

本文主要研究的是竞争性设施选址问题，针对传统企业管理模式下竞争性设施选址研究的不足，从供需网系统的角度，以系统内损最小作为目标研究该问题.由于消费者选择的偏好往往受设施的引力和两者之间距离的影响，因此，本文运用效用函数对消费者决策偏好进行了量化.竞争性设施选址模型求解较为复杂，具有一定的难度，本文根据问题的特点运用了分散搜索算法改善了解的品质，并很大程度上提高了求解速度.

［1］刘彩虹，徐福缘.供应链系统转变为供需网系统研究［J］.运筹学学报，2008，12（4）：113－121.

［2］王志平，王众托.超网络理论及其应用［M］.北京：科学出版社，2008.

［3］Huff D L.Defining and estimating a trade area［J］.Journal of Marketing，1964，28（3）：34－38.

［4］Nakanishi M，Cooper L G.Parameter estimates formultiplicative competitive interaction models least square approach［J］.Journal of Marketing Research，1974，11（3）：303－311.

［5］Aboolian R，Berman O，Krass D.Competitive facility location model with concave demand［J］.European Journal of Operational Research，2007，181（2）：598－619.

［6］Wang Q，Batta R，Bhaduyr J，et al.Budget constrained location problem with opening and closing of facilities［J］.Computers ＆ Operations Research，2003，30（13）：2047－2069.

［7］Glover F.Heuristics for integer programming using surrogate constraints［J］.Decision Sciences，1977，8（1）：156－166.

［8］Burcu B，Uster H.A scatter search－based heuristic tolocate capacitated transshipment points ［J］.Computers ＆ Operations Research，2007，34（10）：3112－3125.

［9］邱模杰，马良.约束平面选址问题的蚂蚁算法［J］.上海理工大学学报，2000，22（3）：217－220.

［10］樊小毛，马良.约束平面选址问题的蜂群优化算法［J］.上海理工大学学报，2010，32（4）：378－380.