变截面框剪结构二阶效应分析的初参数法
张 华,黄 鹂,胡启平
(1.河北科技大学建筑工程学院,河北石家庄 050018;2.河北工程大学土木学院,河北邯郸 056038)
随着建筑物不断向高处发展,结构的侧向刚度相对减小,加之高层建筑巨大的竖向荷载,使结构竖向荷载与水平荷载相互影响的二阶效应分析变得非常重要[1-3]。
框架-剪力墙结构作为传统的三大结构体系之一,其计算理论发展得比较成熟[4-7],但对于变截面框剪结构的简化计算尚有待于进一步完善。笔者曾用状态空间法分析过变截面高层建筑的简化计算问题[8-10],现拟沿用传统假设,采用分段连续化模型,把结构看成变截面剪弯梁,总剪力墙采用弯曲梁模型,总框架采用剪切梁模型[7],对上述模型建立二阶分析的微分方程,写出其矩阵形式的初参数解,以期得到一种简单实用的计算方法。
1 二阶分析的初参数解
高层框剪结构的梁柱截面尺寸或材料强度等级往往沿竖向分阶段变化,形成多阶变截面结构。为了简化计算,并充分考虑多阶变截面的影响,将结构沿竖向分阶段连续化,每一阶段内结构为等截面,并假定仅在楼层标高处作用竖向荷载,将结构按楼层分成n段,如图1所示。
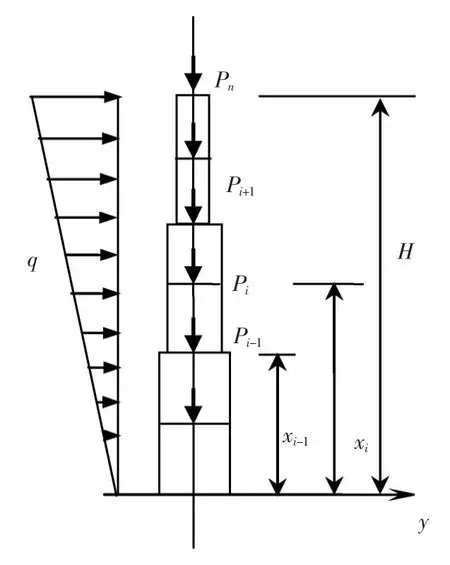
图1 结构计算简图Fig.1 Model of the structure
设结构的总高度为H,第i(i=1,2,…,n)层结构总剪力墙的抗弯刚度为Dwi,总框架的剪切刚度为Cfi,总连梁的约束刚度系数为Cli(它们的定义及求法见文献[5]),轴向压力为Ni(见图2)。
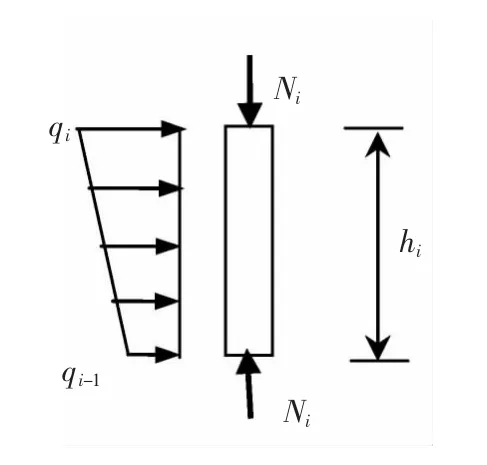
图2 第i层结构受力图Fig.2 Loads of storey i
考虑二阶效应时第i层结构的控制微分方程为[7]
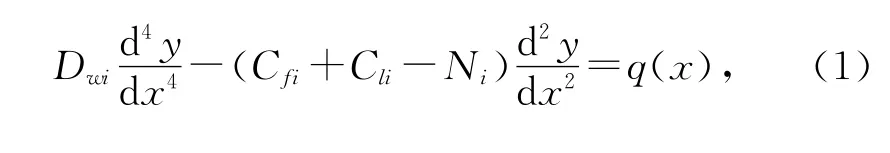
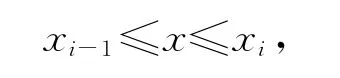
式中Ni=Pi+Pi+1+…+Pn。
结构的转角θ、总剪力墙弯矩Mw、结构的总剪力Q可分别表示为
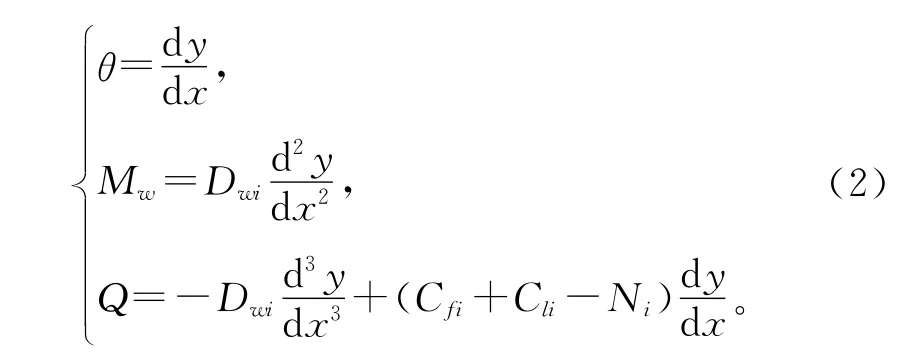
1)当Cfi+Cli-Ni>0时
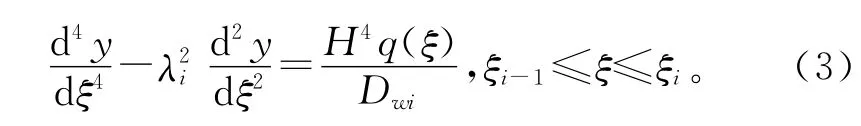
式(3)的初参数形式的解为
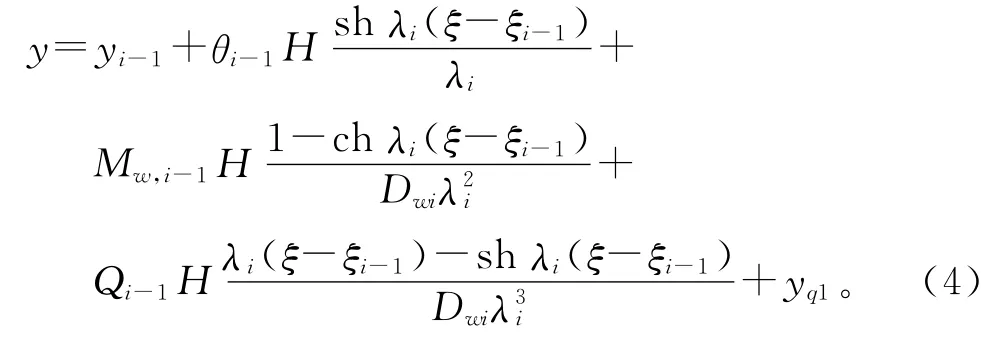
式中:yi-1,θi-1,Mw,i-1,Qi-1分别为第(i-1)层楼板标高处结构的总位移、转角、剪力墙的弯矩和结构的总剪力;yq1为荷载q引起的特解。
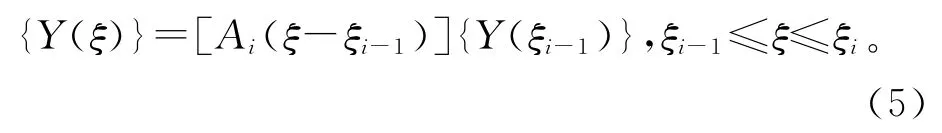
式中
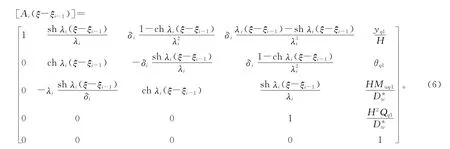
2)当Cfi+Cli-Ni=0时
式(1)改写成式(7)形式。

式(7)矩阵形式的初参数解同式(5),其中:
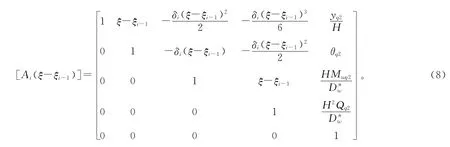
3)当Cfi+Cli-Ni<0时
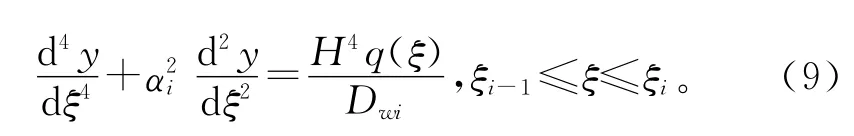
式(9)矩阵形式的初参数解同式(5),其中
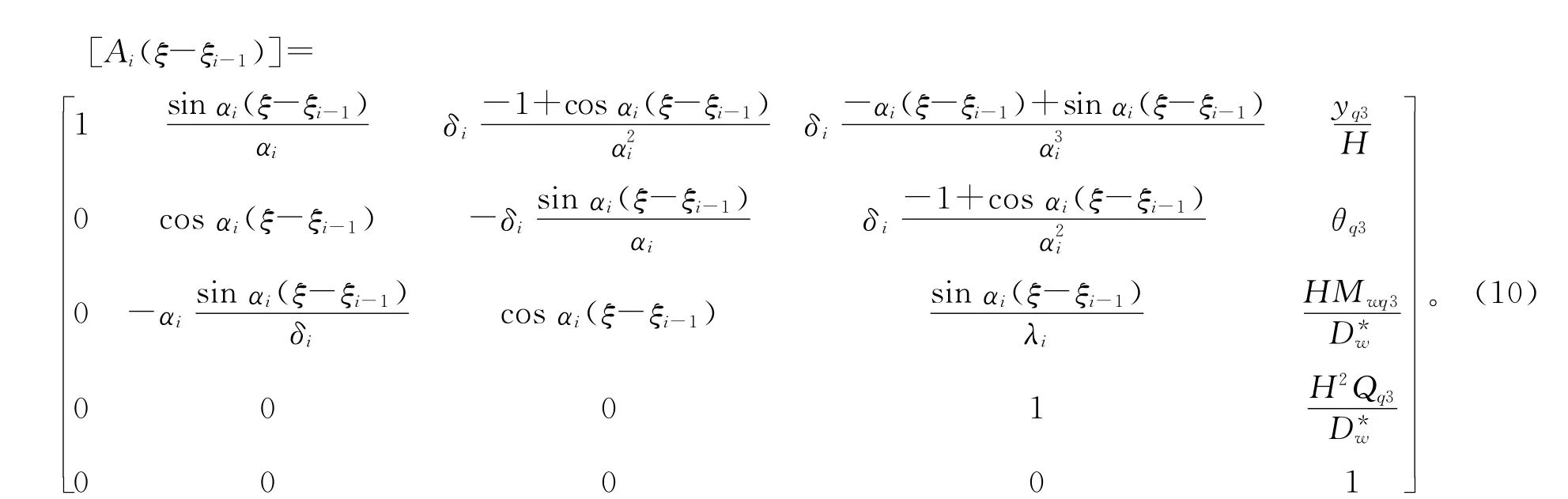
第i层结构的水平荷载一般为梯形分布荷载,设第i层结构层高为hi,则
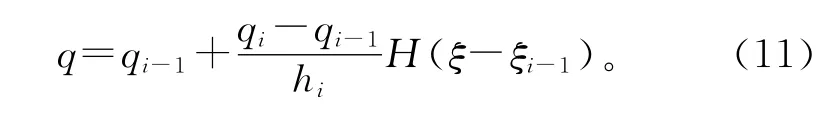
对于上述3种情况,在水平荷载作用下的特解分别为
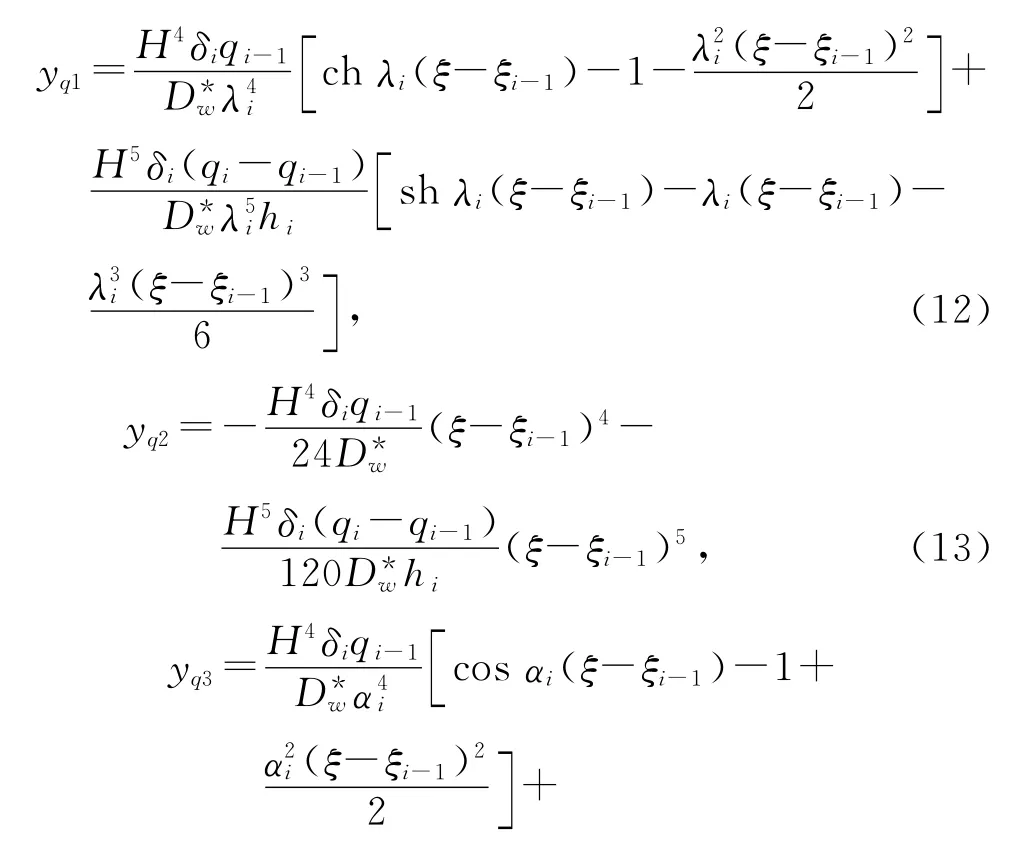
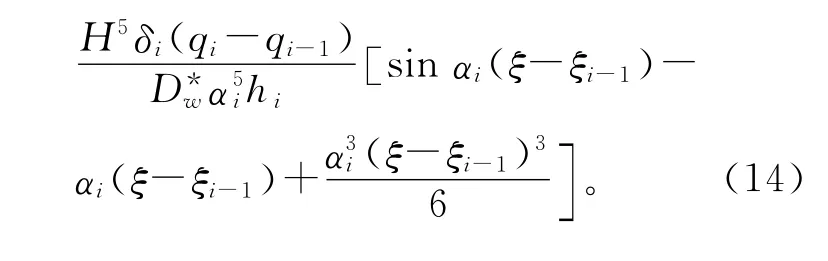
2 内力计算方法
在式(5)中令ξ=ξi可得:

再令[Ai]=[Ai(ξi-ξi-1)],则矩阵[Ai]就是变截面框剪结构二阶分析时第i层结构的传递矩阵。由式(15)递推可得:

记[A]=[An][An-1]…[A1],则五阶方阵[A]即为结构二阶分析时的整体传递矩阵。即
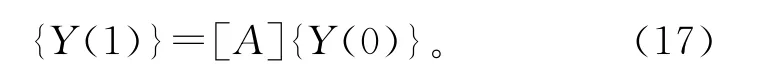
结构的边界条件为
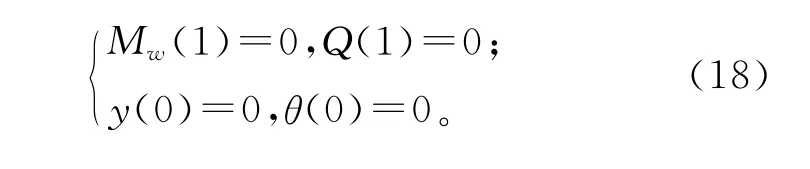
由式(17)及边界条件(18)联立,可以建立一个二元一次方程组,求解这组方程即可确定出问题的初参数,进而可以求出结构任一高度处的内力和变形。
3 算 例
某20层框-剪结构,层高h=4.2m,总高度H=84m,建筑物总重G=305 760kN,经计算Dw=7.00×109kN·m2,Cf=3.59×106kN,Cl=1.68×106kN。建筑物承受倒三角形分布水平荷载作用,顶部的荷载集度q=250kN/m。按本文计算方法算出的部分楼层的水平位移等参数,以及文献[7]的计算结果见表1。

表1 结构的水平位移及内力Tab.1 Lateral displacement and internal forces
本文算例的计算结果与参考文献[7]中的计算结果非常接近,说明了初参数法的正确性和合理性。此外本文是先写出微分方程矩阵形式的初参数解,然后只需在MATLAB中简单编程即可求出结构在任一位置处的变形和内力,其思路简捷,计算方便,是一种合理、实用的简化计算方法。
/References:
[1]肖从真,王翠坤,张维嶽.高层建筑的重力二阶效应分析方法与主要影响因素[J].建筑科学,2003(8):14-16.XIAO Congzhen, WANG Cuikun,ZHANG Weiyue.P-Δeffect and its main influential factors for tall building[J].Building Science,2003(8):14-16.
[2]包世华,龚耀清.超高层建筑空间巨型框架的水平力和重力二阶效应分析新方法[J].计算力学学报,2010(2):40-46.BAO Shihua,GONG Yaoqing.A new method for second-order effect analysis on spacial mega frame of super tall buildings due to both horizontal and vertical loadings[J].Chinese Journal of Computational Mechanics,2010(2):40-46.
[3]林聪云.低层钢框架结构二阶效应分析[J].福建建材,2011(2):5-7.LIN Congyun.Second-order effect analysis of low-rise steel frames[J].Fujian Building Materials,2011(2):5-7.
[4]董 庆,林 雁.框架-剪力墙结构的简化分析方法[J].山西建筑,2008(9):98-99.DONG Qing,LIN Yan.The simplified analysis of frameshearing wall structure[J].Shanxi Architecture,2008(9):98-99.
[5]高宏俊,王羡农,闫亚光,等.框剪结构协同分析的状态空间法[J].西安科技大学学报,2007,27(4):573-575.GAO Hongjun,WANG Xiannong,YAN Yaguang,et al.Coordination analysis of frame-shear wall structure[J].Journal of Xi′an University of Science and Technology,2007,27(4):573-575.
[6]梁启智,谢 理.框-剪结构的二阶分析[J].建筑结构学报,1986(5):1-8.LIANG Qizhi,XIE Li.The second order analysis of frame-shear wall structure[J].Journal of Building Structures,1986(5):1-8.
[7]叶文洪,梁启智.考虑二阶效应时框剪结构的简化分析[J].工程力学,1999(2):26-34.YE Wenhong,LIANG Qizhi.A simplified analysis of frameshear wall structure considering second order effects[J].Engineering Mechanics,1999(2):26-34.
[8]张 华,位翠霞,黄 鹂.变截面框剪结构二阶效应分析的精细积分法[J].河北科技大学学报,2012,33(4):151-154.ZHANG Hua,WEI Cuixia,HUANG Li.The state space method of second order analysis for frame-shear wall structures with stepped parameters[J].Journal of Hebei University of Science and Technology,2012,33(4):151-154.
[9]张 华,杜现奇.框架-剪力墙-薄壁筒斜交结构自由振动分析的状态空间法[J].河北工业科技,2010,27(3):192-195.ZHANG Hua,DU Xianqi.Free vibration analysis of frameshear wall-thin walled core skew combined structure by using state space method [J].Hebei Journal of Industrial Science and Technology,2010,27(3):192-195.
[10]胡启平,张 华.框架-剪力墙-薄壁筒斜交结构分析的状态空间法[J].工程力学,2006(4):125-129.HU Qiping,ZHANG Hua.State space method for the analysis of frame-shear wall-thin walled core skew combined structure by using state space method[J].Engineering Mechanics,2006(4):125-129.

