海潮改正模型对GPS基线的影响
汪 利,吴北平,何光滔,杨 虎
(1.中国地质大学 信息工程学院,湖北 武汉 430074)
由于地球表面及其内部有一定的弹性,在受力的情况下会发生变形,因此,日月对地球的引力作用,会使海洋产生潮汐形变,使实际海平面相对于平均海平面产生周期性的涨落(海潮),同样海潮引起的海水质量重新分布也会使固体地球产生弹性形变,这就是海洋潮汐负荷[1](Ocean Tide Loading ,简称 OTL)。在沿海地区海洋潮汐负荷对GPS测量的垂直方向的影响可达cm级[2],虽然在水平方向影响比较小,但是在高精度GPS定位中还是不能被忽略。因此在高精度GPS数据处理中必须考虑海洋潮汐负荷的改正,如美国的GAMIT软件和中国的PANDA软件都考虑到海潮模型的改正。郑祎等利用NAO99b全球海潮模型计算了中国IGS站的海潮改正,并对是否加载海潮模型进行了基线和坐标的比较[3];Ta-Kang等对台湾的GPS测站进行研究,证明了海洋潮汐负荷对GPS测站的垂直方向影响为13~27 mm[4]。但是国内对不同的海潮改正模型以及海潮改正对GPS影响的周期研究较少,为此笔者利用4种海潮改正模型进行了对比分析,并比较了沿海和内陆地区GPS联测的基线,最后用功率谱分析中的周期图法进行了周期的估计,得到了海洋潮汐负荷对GPS基线分量的影响周期。
1 海潮位移改正模型
在球坐标系中,海潮对测站位移的影响可用褶积积分来表示:
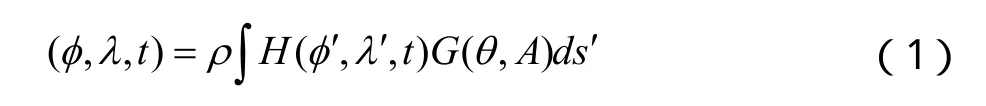
式中,ρ为海水的密度; 和 分别为测站和负荷点的球坐标;A、θ为测站到负荷点的方位角和极距;ds'为负荷面元;H为瞬时潮高;G为格林函数。其中:

式中,∆r、∆φ、∆λ分别为海潮负荷引起的测站垂直方向、南北方向和东西方向的改正。
垂直和水平方向的格林函数G分别为:
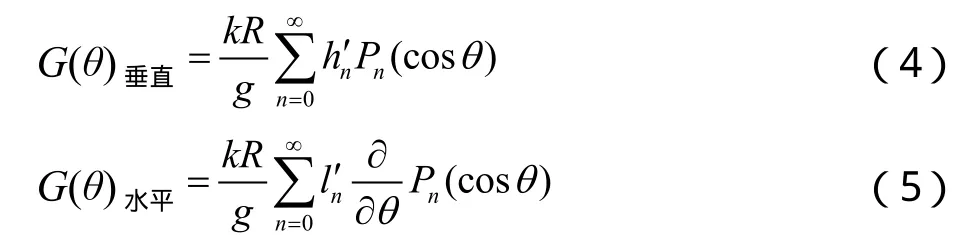
式中,k为引力常数;R为地球半径;g为重力常数;hn′和ln′为n阶负荷勒夫数,其值可依据地球内部结构模型求解[5,6]。
2 海潮负荷模型的对比与分析
2.1 数据处理与不同海潮模型之间的比较
本文利用GAMIT10.04软件[7]计算了2011年1月1日到2011年7月19日,共计200 d国内9个IGS站(URUM、WUHN、TWTF、SHAO、XIAN、BJFS、LHAZ、CHAN、KUNM)的GPS数据,计算时考虑采用未加入以及分别加入4种不同的全球海潮改正模型(CSR4.0、GOT00.2、FES2004和TPXO7.0)等情况。所有的海潮改正数据均来自Scherneck的免费海洋潮汐负荷网站(http://froste.oso.chalmers.se/loading),每个海潮改正模型均有11个分潮波,每个分潮波有3个方向的振幅和相位,只要在Scherneck提供的数据文件最前面加入1行GAMIT所识别的模型和参考框架(E为固体地球参考中心、M为地球系统参考中心)参数[8],并将其连接到otl.list文件就可以在GAMIT中使用。本文的各种海潮模型均选用地球系统参考中心,对URUM(乌鲁木齐)站进行紧约束,利用IGS站的精密星历,得到每天每种模型的基线分量(N、E和U 3个方向),再将基线分量减去相应的未加海潮改正的基线分量,得到海潮改正影响引起的基线分量的差值。限于篇幅,下面以基线URUM-TWTF进行说明,4种不同海潮模型对基线URUM-TWTF的N、E和U 3个方向的影响如图1所示。

图1 基线URUM-TWTF的不同海潮模型的比较
通过图1,我们可以看出4种不同的海潮改正模型对基线URUM-TWTF的分量影响基本相同,它们之间的差别绝大部分在0.1~0.3 mm。所以在进行高精度GPS数据处理时,可以不必过分地追求使用哪种海潮改正模型。由图1我们还可知,海潮改正对垂直方向的影响比对水平方向的影响大,垂直方向的影响大约是水平方向的影响的3倍;并且海潮改正对GPS基线的影响呈周期变化,尤其是垂直方向的周期性比较明显。为了说明海潮改正模型对内陆和沿海GPS测站影响的区别,笔者比较了TPXO7.0改正模型下的URUM-TWTF(乌鲁木齐到台湾)和URUM-LHAZ(乌鲁木齐到拉萨)2条基线,如图2所示。通过比较可知,海潮改正模型对含沿海地区测站的影响比只含内陆地区测站基线的影响大,含沿海地区GPS基线垂直方向的影响能到达1~2 cm,而只含内陆地区GPS基线的影响在垂直方向的影响都在6 mm以下,并且水平方向上的影响都在mm级,所以在进行含沿海地区GPS测站的高精度数据处理时必须加入海潮改正模型。
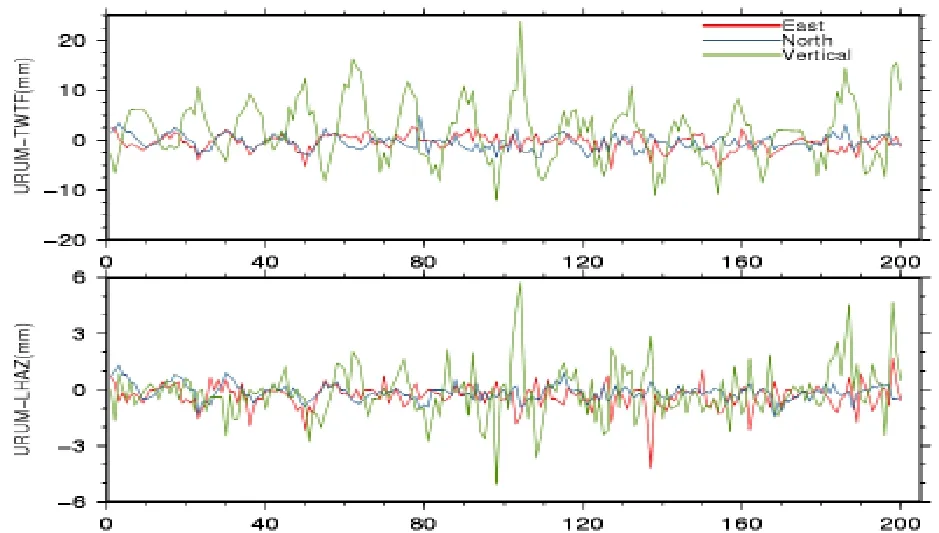
图2 基线URUM-TWTF与基线URUM-LHAZ对比图
2.2 功率谱估计海潮改正的周期
为了说明海潮改正模型对GPS影响呈周期性变化,笔者用功率谱估计中的周期图法估计了TPXO7.0模型下URUM-TWTF基线3个方向的周期。周期图法是把随机序列x(n)的N个观测数据视为1个能量有限的序列,直接计算x(n)的离散傅立叶变换,得到X(k),然后再取其幅值的平方,并除以N,作为序列x(n)真实功率谱的估计[9]。通过周期图法,得到基线URUM-TWTF 3个方向的功率谱密度,图3为垂直方向的功率谱密度图。

图3 基线URUM-TWTF垂直方向的功率谱图
通过垂直方向的功率谱图分析可知,海潮改正对垂直方向的影响呈较明显的周期性,海潮改正模型在200 d内对GPS基线垂直方向的影响有14.435个周期,换言之,海潮改正对基线的影响周期约为13.855(200/14.435)d,这一结果与Fu Yuning等人用精密单点定位得到的13.67 d非常接近[10]。而对于水平方向的周期性影响没有垂直方向那么明显,但是影响周期却非常接近,分别是13.902 d(N方向)和13.828 d(E方向)。
3 结 语
综上所述,不同的海潮改正模型对基线改正的结果差别很小,但是是否加入海潮改正对GPS基线解算结果有一定的影响,特别是包含沿海地区GPS测站的基线,垂直方向的影响最大能达2 cm,水平方向的影响基本在mm级,所以在高精度GPS数据处理过程中必须考虑海潮模型的改正,以提高GPS数据解算的精度及解算结果的稳定性和可靠性。
[1]徐晓庆.中国近海和中国及邻近大陆海潮负荷效应的计算[D].青岛:国家海洋局第一海洋研究所,2011
[2]文援兰.卫星导航系统分析与仿真技术[M].北京:中国宇航出版社,2009
[3]郑祎,伍吉仓,王解先,等.GPS精密定位中的海潮位移改正[J].武汉大学学报:信息科学版,2003,28(4):405-408
[4]YEH T,HUANG C,XU G C.GPS Height and Gravity Variations Due to Ocean Tidal Loading Around Taiwan[J].Surveys in Geophysics,2008,29(1):37-50
[5]刘友文,姜卫平,鄂栋臣,等.南极国际GPS联测的海潮位移改正[J].武汉大学学报:信息科学版,2007,32(10):899-901
[6]郑祎,伍吉仓,王解先,等.中国地壳运动观测网络的海潮位移改正系数[J].同济大学学报,2002,30(11):1 365-1 369
[7]赵建三,杨创,闻德保.利用GAMMIT进行高精度GPS基线解算的方法及精度分析[J].测绘通报,2011(8):5-8
[8]Department of Earth,and Planetary Sciences Massachusetts Institute of Technology.GAMIT Reference Manual.Release10.40.[S].USA: MIT,2010
[9]郑君里.信号与系统(上册)[M].北京:高等教育出版社,2000
[10]FU Y N,FREYMUELLER J T,DAM T V.The Effect of Using Inconsistent Ocean Tidal Loading Models on GPS Coordinate Solutions[J].Journal of Geodesy,2011

