一种可快速编码的QC-LDPC码构造新方法
刘原华 ,张美玲
(西安邮电大学通信与信息工程学院,西安710121)
1 引 言
低密度奇偶校验码(LDPC码)具有逼近Shannon限的纠错性能,近年来成为编码领域的研究热点,目前已广泛应用于深空通信、光纤通信和卫星数字视频广播等领域。根据构造方法的不同,可将LDPC码分为两大类:随机LDPC码和结构化LDPC码。随机LDPC码的编码复杂度与码长的平方成正比,且校验矩阵的硬件存储也较为复杂,这已成为LDPC码实用化的一个瓶颈。为了实用的目的,需要设计性能优良、校验矩阵具有一定结构特性的 LDPC码。基于循环置换矩阵的QC-LDPC码[1-2]是一种结构化LDPC码,已经得到编码领域学者的研究和关注。
基于循环置换矩阵的QC-LDPC码的校验矩阵由循环置换矩阵构成,通过恰当地选择循环置换矩阵可以避免相应Tanner图中的短环。文献[3]和[4]分别利用欧氏几何和有限域的特性构造出了不包含4环的性能优异的QC-LDPC码。值得注意的是,该类码的设计不仅需要避免短环,还需要考虑校验矩阵的行相关问题。文献[5]在提出了一种QC-LDPC码构造方法的同时分析了校验矩阵的行相关问题。一般设计的QC-LDPC码并不能保证校验矩阵的满秩,即存在行相关问题,而校验矩阵的行相关问题将会导致构造生成矩阵非常困难[6]。为解决行相关问题,IEEE 802.16e标准中采用具有特殊结构的QCLDPC码,其校验矩阵的右半部分具有准双对角线结构,满足非奇异性,即满秩,并且可直接利用校验矩阵进行编码,具有很低的编码复杂度。然而,IEEE 802.16e标准中的LDPC码校验矩阵右半部分双对角线上的子矩阵均是单位阵,限制得较为严格,使很多好码被排除在外。综合考虑以上两方面,本文利用已有的基于循环置换矩阵的QC-LDPC码,通过打孔和行置换,获得了一大类性能优异且可实现快速编码的QC-LDPC码。与IEEE 802.16e标准中的LDPC码相比,本文构造出的QC-LDPC码具有相同的编码复杂度,且具有更优的纠错性能。
2 基于循环置换矩阵的QC-LDPC码
基于循环置换矩阵的QC-LDPC码的校验矩阵H由循环置换矩阵和零矩阵组成:

式中,aij∈{-1,0,1,2,…,n-1},Iaij为一个n×n的循环置换矩阵,可由单位阵 I每行向右循环移位aij位得到,I-1表示全零矩阵。H的零空间即为码长为N=nρ的QC-LDPC码。每个循环置换矩阵均可由其维数n和循环移位次数aij唯一确定,因此 H所需的存储空间非常小。矩阵 H的基矩阵Hb定义为如下γ×ρ矩阵:

将 Hb中的aij用n×n的循环置换矩阵Iaij代替,即可得到矩阵H,称为矩阵扩展。
Tanner等在文献[1]中构造的LDPC码就是一种基于循环置换矩阵的QC-LDPC码,对任意素数 p,选取域GF(p)中的非零元素a和b,a和b的阶分别为k和j,Tanner构造的QC-LDPC码的基矩阵如式(3),校验矩阵可由基矩阵扩展得到,即将基矩阵中的每一元素用对应的p×p的循环置换矩阵代替。
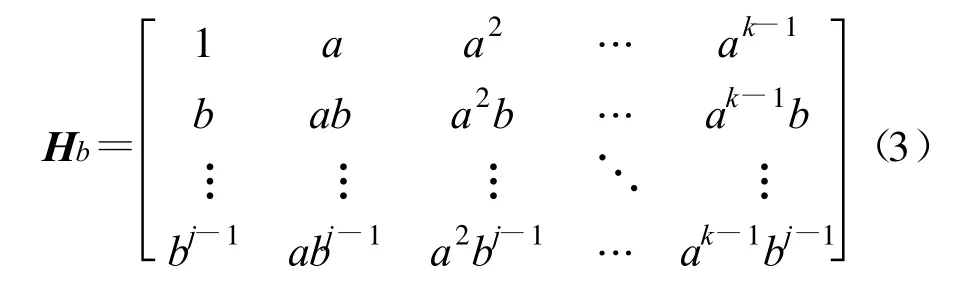
3 可快速编码的QC-LDPC码设计
IEEE 802.16e标准中的QC-LDPC码是一种基于循环置换矩阵的QC-LDPC码,校验矩阵可由其基矩阵扩展得到,且校验矩阵的右半部分具有准双对角线结构,保证了校验矩阵的满秩,同时可直接利用校验矩阵进行编码。然而,IEEE 802.16e标准中QC-LDPC码的校验矩阵右半部分双对角线上的子矩阵均是单位阵,要求比较严格,很多好码被排除在外。事实上,可以证明,若校验矩阵的右半部分具有准双对角线结构,则只要保证双对角线上同一块列的子矩阵相同,即可使校验矩阵满秩,并可直接利用校验矩阵进行低复杂度的迭代编码。由此,提出了一种具有如此结构的校验矩阵的设计方法,从而获得可实现低编码复杂度的QC-LDPC码。下面进行详细说明。
将具有上述结构的校验矩阵分成两部分:

其中,H1的维数为m×k(m=pmb,k=pkb),H2的维数为m×m,且 H2具有式(5)形式,其中 Ix在H2的第r块行,可以证明H2满秩。

定理1 具有式(5)形式的矩阵是满秩的。
证明:以块为单位,从下往上将分块矩阵H2的各块行与其后的所有块行进行模2加得到一个新的块行,该变换实际上是对矩阵H2做初等行变换:


许多文献[1-4]提出了基于循环置换矩阵的QCLDPC码的构造方法,构造出的校验矩阵是非满秩的,致使由校验矩阵构造生成矩阵非常困难。为降低LDPC码的编码实现复杂度,本文提出了一种新的可实现快速编码的QC-LDPC码构造方法,该方法在原始校验矩阵的基础上利用打孔和行置换操作,使校验矩阵的右半部分具有式(5)的形式,从而保证所构造的校验矩阵满秩,可直接利用校验矩阵进行低复杂度编码。图1给出了新构造方法的实现流程图。

图1 新构造方法的流程图Fig.1 Flowchart of the new design method
以M为校验矩阵,其零空间即为可快速编码的QC-LDPC码。其中第一步中,可利用已有的各种基于循环置换矩阵的QC-LDPC码构造方法来获得原始矩阵H。
第二步中打孔矩阵Z的构造方法如下:若矩阵H为由子矩阵组成的γ×ρ的矩阵阵列,则打孔矩阵Z=[zij]为GF(2)上的 γ×ρ矩阵,将Z分成两部分Z=[Z1Z2],其中 Z2为具有式(8)的形式的 γ×γ矩阵,第一列中间的1在第 r行,Z1为全1矩阵。

第三步中的打孔过程可以看作是一种特殊的矩阵乘法运算,矩阵阵列H的打孔定义为GF(2)上的打孔矩阵Z与H的乘积:
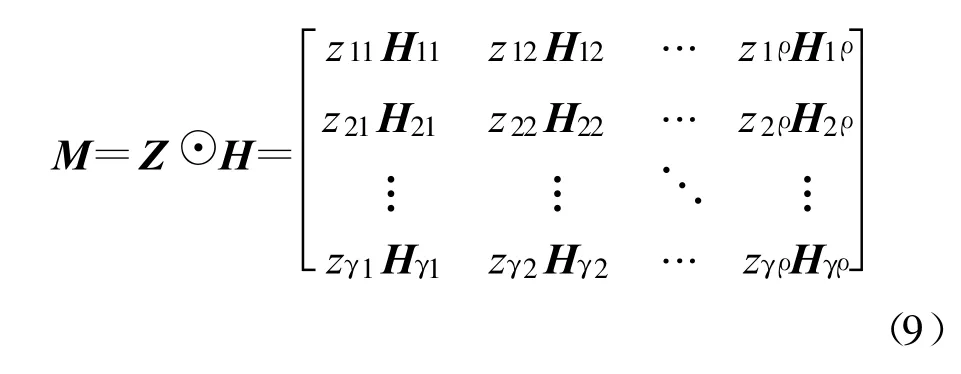
若 zij=1,则zijHij=Hij;若 zij=0,则 zijHij=0 为全零矩阵。可以看出,如果 Z中含有0元素,则打孔后的矩阵M更稀疏;如果 H不包含四环,则 M也不包含四环。
下面给出如何对M 进行循环移位使其右半部分具有式(5)的形式。记矩阵M=[M1M2]的右半部分M2第 i行j列的子矩阵为M2(i,j),以块为单位,将M的第i块行向左循环移S(i)位,其中S(1)=0,S(i)=M2(i,i)-M2(i-1,i)+S(i-1),2≤i≤γ,同时令 M2(γ,1)=M2(1,1),则可使 M2具有式(5)的形式,即可保证矩阵M满秩,并可直接利用M进行迭代编码。由于M的子矩阵为循环置换矩阵,这样的循环移位仅相当于对M 做行置换,将循环移位前后的M作为校验矩阵所获得的QC-LDPC码的纠错性能完全相同。
下面给出如何直接利用M进行简单快速编码。对于系统码,码字向量可表示为c=[s p],其中s=[s1s2…skb]为信息向量,p=[p1p2…pmb]为校验向量,且 si和pi的长度均为p。由M·cT=0可得M1·sT=M2·pT。记Mb1为 M1的基矩阵,第 i行第j列的元素为Mb1(i,j),则
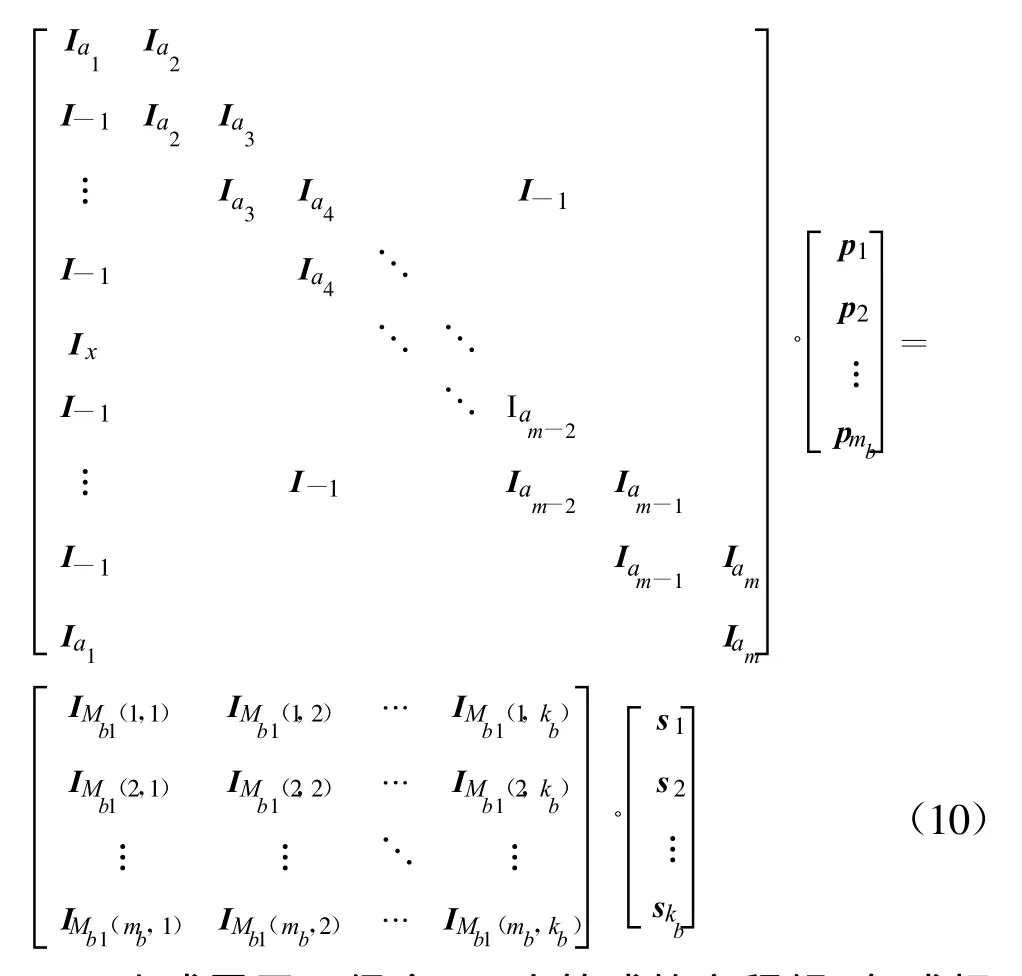
上式展开可得含mb个等式的方程组,各式相加可得
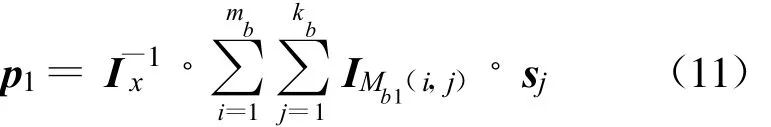
将式(11)代入式(10)中的每个等式可得
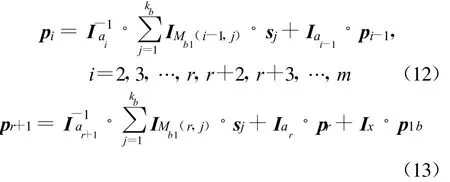
式(11)~(13)为计算pi的迭代公式,从而得到校验向量 p。下面考虑编码复杂度,矩阵Ia为循环置换矩阵,每行每列仅有一个1,因此式(11)~(13)的主要计算量在于,由此可知,求校验向量的计算量与802.16e标准中求校验向量的计算量相同。
4 仿真结果
本节采用BPSK调制下的加性高斯白噪声信道(AWGN),仿真比较新方法构造的QC-LDPC码和IEEE 802.16e标准中的QC-LDPC码在置信传播(BP)译码算法下的纠错性能,BP算法的最大迭代次数均设为50次。
图2显示了1/2码率的新方法构造码与IEEE 802.16e中的码的BER性能。新构造方法的第一步选用文献[1]中的构造方法,码(696,348)的构造参数如下:p=29,a=2,b=3,a和b的阶均为28,由此可构造出子矩阵组成的28×28的矩阵阵列,选前12行24列子矩阵作为码(696,348)的原始矩阵 H。码(2328,1164)的构造参数如下:p=97,a=2,b=3,a和b的阶均为48,由此可构造出48×48的矩阵阵列,选前12行24列子矩阵作为码(2328,1164)的原始矩阵 H。为增强可比性,打孔矩阵 Z的构造如下:将1/2码率的IEEE 802.16e码的基矩阵中的-1用0代替,非-1用1代替得到的矩阵为打孔矩阵Z。打孔后得到具有准双对角线结构的满秩矩阵M。然后以块为单位,将M的第i块行向左循环移S(i)位,最后令M2(γ,1)=M2(1,1)。M 的零空间即为构造的QC-LDPC码。

图2 新方法构造码与IEEE 802.16e码的BER性能Fig.2 Performance of the new codes and the codesin IEEE 802.16e
由仿真结果可以看出,新方法构造的码BER性能略优于IEEE 802.16e中的码。由上一小节中编码实现的分析可知,新方法构造的码与IEEE 802.16e中的码具有相同的编码复杂度,即新方法构造的码在保证低编码复杂度的基础上获得了更优的纠错性能。同时需要指出的是,IEEE 802.16e标准中的码结构限制得较为严格,使很多好码被排除在外,新方法可以在任意已有的基于循环置换矩阵的构造方法基础上进行打孔和行置换操作,从而可以构造出一大类性能优异的可实现快速编码的QC-LDPC码。
5 结束语
本文研究了基于循环置换矩阵的QC-LDPC码构造方法,发现已有的大部分设计方法构造的QCLDPC码存在校验矩阵的行相关问题,导致编码复杂度较高。由此,提出了一种新的可快速编码的QCLDPC码构造方法,在已有的各种基于循环置换矩阵的QC-LDPC码构造方法基础上,通过打孔和行置换,使校验矩阵具有准双对角线结构,可以利用校验矩阵直接进行简单快速的编码,在保证优异性能的同时,降低了LDPC码的硬件实现复杂度。同时给出了简单快速编码的具体实现方法,并分析比较了编码实现复杂度。仿真结果表明,与IEEE 802.16e标准中的LDPC码相比,新方法构造出的QC-LDPC码在保证低编码复杂度的基础上获得了更优的纠错性能。
[1]Tanner R M,Sridhara D,Sridharan A,et al.LDPC block and convolutional codes based on circulant matrices[J].IEEE Transactions on Information Theory,2004,50(12):2966-2984.
[2]Fossorier M P C.Quasi-cyclic low-density parity-check codes from circulant permutation matrices[J].IEEE Transactions on Information Theory,2004,50(8):1788-1793.
[3]Liu Yuanhua,Niu Xinliang,Wang Xinmei,et al.Design of quasi-cyclic LDPC codes based on Euclidean geometries[J].Journal of Electronics(China),2010,27(3):340-344.
[4]Zhang L,LinS,Abdel-Ghaffar K,et al.Quasi-cyclic LDPC codes on cyclic subgroups of finite fields[J].IEEE Transactions on Communications,2011,59(9):2330-2336.
[5]Liu K,Huang Q,LinS,et al.Quasi-cyclic LDPC codes:Construction and rank analysis of their parity-check matrices[C]//Proceedings of 2012Information Theory and Applications Workshop(IT A).San Diego,CA:IEEE,2012:227-233.
[6]Zhao Ying,Xiao Yang.The necessary and sufficient condition of a class of quasi-cyclic LDPC codes without girth four[J].IEICE Transactions on Communications,2009,92(1):306-309.

