基于分布式光纤测温系统的单芯电缆瞬态温度场数值计算

邢 雅， 侯 喆， 杨宇琦， 李洪杰

(西安交通大学电气工程学院，陕西西安710049)

0 引言

随着城市电网的不断发展，交联聚乙烯(XLPE)电力电缆在电力系统中的应用越来越普及。为了保证电缆长期可靠、经济地运行，采用精确的方法计算电缆的温度分布以及载流量是非常重要的。目前，35 kV等级以上的电力电缆基本都安装了电缆温度在线监测系统，重要线路的高压和超高压电缆已沿线安装了分布式光纤温度测量系统(DTS)，采用DTS可以实时沿线监测电缆表面温度［1-2］。电缆的载流量取决于导体的最高持续运行温度。计算电缆载流量主要有两种方法:一种是基于国际电工委员会IEC 60287标准的热路分析法［3-5］;另外一种是数值计算方法，常用的数值计算方法有边界元法、有限差分法、有限容积法及有限元法［6-11］。鉴于有限元法能够方便地应对各种复杂的电缆敷设环境和边界条件，本文采用有限元法，结合实时负荷和DTS所测电缆表面温度间接对电缆的瞬态温度场进行分析计算。

目前，有相当多的文献使用有限元方法已经对XLPE电缆的载流量进行了研究，很多的计算研究是基于大型通用有限元软件的［12-14］，如 ANSYS，COMSOL Multiphysics等。然而，通用有限元软件对于导体负荷及电缆表面温度实时变化的瞬态温度场的计算具有局限性。考虑到自主编制场域剖分程序较为复杂，本文利用通用有限元软件ANSYS对计算场域进行自动划分，提取得到的单元与节点的相关信息，利用有限元法的基本原理，自主编制有限元的计算程序，分析计算了单芯电缆的瞬态温度场。

为了验证计算结果的正确性，对一根单芯110 kV 1×630 mm2XLPE电缆开展了试验研究。试验结果表明，自主编制的有限元计算程序结果与试验结果基本一致，验证了该方法的准确性，最后对两者差异的原因进行了分析。

1 瞬态温度场有限元计算原理

电缆的瞬态温度场属于二维导热问题，并且考虑热容的影响。对于具有内热源的区域，温度控制方程为:

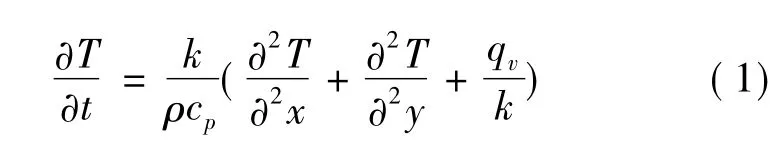
式中，x，y为空间坐标(m);T为瞬态温度(K);ρ为相应材料的密度(kg/m3);cp为比热容(J/kg/K);k为热导率(W/m/K);t为时间(s);qv为产热率(W/m3)，对于无内热源的区域，qv值为0。

为了得到固体导热偏微分方程的唯一解及电缆瞬态温度场，必须附加边界条件和初始条件，统称为定解条件，与微分方程联立求解，边界条件有三种，第一类边界条件为边界上的温度为已知

第二类边界条件为已知边界法向的热流密度

式中，q为热流密度(W/m2)。

第三类边界条件为对流边界条件，已知对流换热系数和环境温度

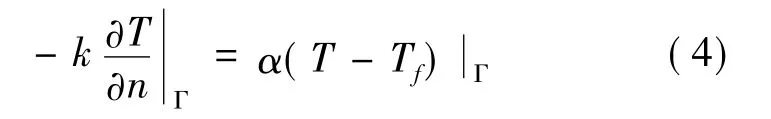
式中，α为对流换热系数(W/m2/K);Tf为环境温度(K)。

导热区域任意点(x，y)的初始条件为:

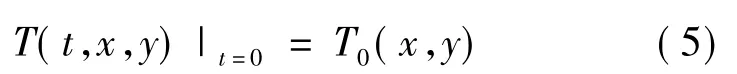
温度场有限元法的计算基本方程可以从泛函变分求得，也可从微分方程出发用加权余量法求得，在加权余量法中，Galerkin法应用更为广泛。如果区域D划分为E个单元和n个结点，则温度场T(t，x，y)离散为T1，T2，…Tn等n个结点的待定温度值，利用Galerkin法推导出单元内的有限元基本方程［15］

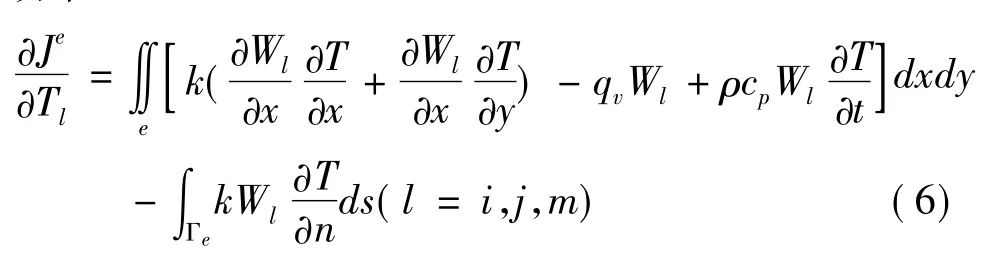
式中，权函数 Wl= T/Tl，上下角标 e 表示单元，i，j，m是单元的局部结点号，也就是三角形单元的三个顶点。下标l的定义具有双重性，在D中它代表整体结点号，而在e中它代表局部结点号。每个单元的局部结点号与整体结点号之间都有严格的对应关系，作为单元信息的一部分编码在需要输入的原始数据中。

对整个区域合成整体的代数方程组

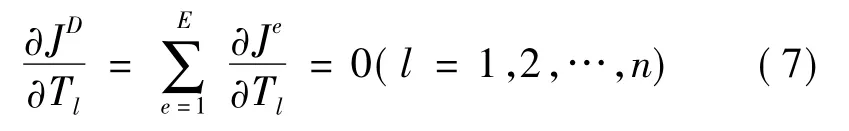
方程组(7)有n个代数式，就可以解出n个结点温度。合成的过程中，同一单元中的相邻节点在合成的时候对该节点方程的系数值有贡献，而不在同一单元中的其余节点就不会有所贡献，利用三角形单元的面积积分，计算出单元的系数项并叠加到整体的系数项中去，得到n个常微分方程

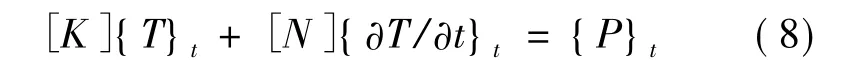
式中，［N］为热容矩阵;［K］为热导矩阵;{P}为产热向量。

对于瞬态分析而言，温度需要在时域进行离散化。采用后向差分形式，则式(8)可变成如下形式:

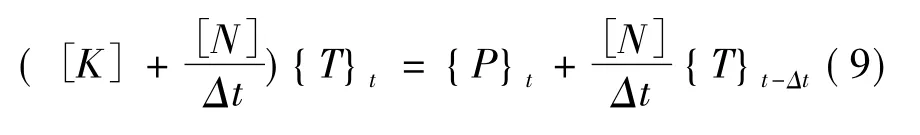
2 温度场求解区域单元划分

对于图1中的边界为Γ的区域D，可以使用三角形单元对其进行划分，划分结束后，每一个结点都有对应的数字序号1，2，…n;每一个单元同样有自己的编号①，②…等。单元通过三个顶点与其他相邻的单元相联系，对每个单元来说，三个顶点用i，j，m按照逆时针编号。对于内部单元，i，j，m可任意按逆时针方向编排，对于边界单元，规定只有一条边(并且编号为j，m)位于边界上，结点i与边界相对。

对于任意单元，划分之后三个顶点坐标都是已知的，三角形中的任意一点的温度T，利用有限单元法把它离散到节点 i，j，m 上去，用 Ti，Tj，Tm表示单元中的温度场T:

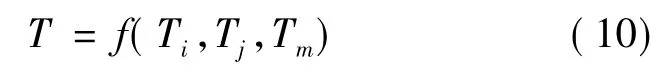
求温度场时只需要求出离散的结点温度，Ti，Tj，Tm，不做连续温度T的计算。

对待计算区域进行单元划分时，尽量使每个三角形单元接近等边三角形，使得计算更为精确。本文使用大型通用有限元仿真软件ANSYS对电缆导热区域进行单元划分，导出单元编号，结点编号以及结点的坐标信息，用于后续编制有限元程序。

图1 区域D内三角形单元划分

3 实例分析与试验验证

3.1 实例计算

为了验证本文提出有限元方法的正确性，选用单根YJLW03 64/110 kV 1×630 mm2XLPE电力电缆，结合试验所测实时变化的负荷电流及DTS所测电缆表面温度，利用所编制的有限元程序计算该电缆瞬态温度分布。电缆导体为紧压圆形绞合铜导体，电缆的结构参数如表1。

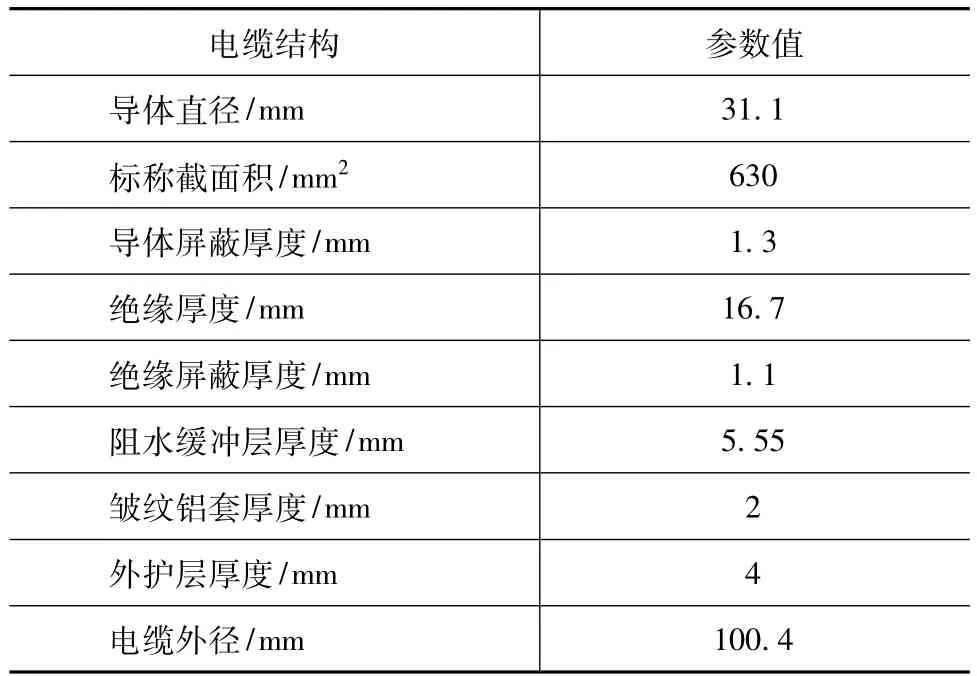
表1 电缆基本结构参数

对于表面温度已知的电力电缆，待求解区域为电力电缆本身，边界条件为第一类边界条件，对于瞬态的温度场，边界条件随时间变化，计算时假设在一个采样周期内保持不变。电缆导热区域的初始条件取值为测量的第一个时刻的电缆表面温度。

对求解温度场区域进行三角形网格剖分，总的来说，网格划分得越小，计算的精度越高，但考虑到瞬态温度场的计算需要迭代计算多次，网格划分太细会导致结点数目增多，使得迭代一次计算时间过长。因此，在温度变化剧烈的地方划分较密，其余地方划分较稀疏，这样就可以在不增加单元和结点数目的条件下提高计算精度和速度。本例中对每一层材料都进行建模剖分，剖分之后的结点数为1913个，单元数为3712个。电缆区域的剖分如图2。

图2 电缆区域有限元剖分图

整个求解区域的损耗主要包括导体损耗、绝缘层损耗、铝护套损耗，损耗的计算可参考IEC 60287标准计算。对于瞬态温度场而言，各部分损耗随着负荷电流的变化而变化，每次迭代都需要更新各部分的损耗。具体的计算过程见流程图3。

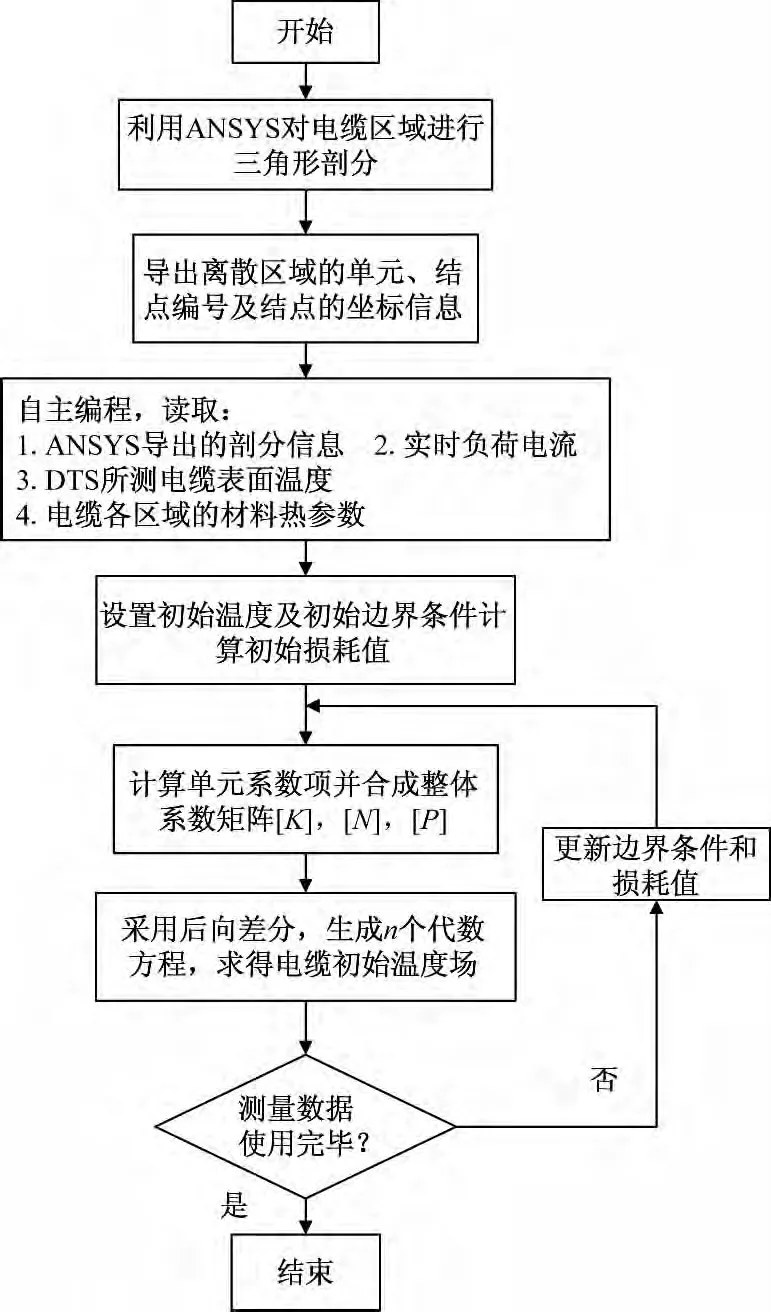
图3 单芯电缆瞬态温度场计算流程图

3.2 试验验证

采用与计算相同的YJLW03 64/110 kV 1×630 mm2XLPE电力电缆作为试验样品，试验电缆长18 m，试验原理图如图4。其中T1为调压器，T2为电缆试验变压器，另外使用电流互感器测量导体负荷电流。为保证能够获得足够的导体温度数据样本，避免因安装和运行过程中的热胀冷缩等不确定因素对导体温度数据影响，在被试电缆上安装3个热电偶实时监测电缆导体的温度。同时利用DTS实时测量电缆表面温度，热电偶和DTS的安装位置如图5。试验电缆导体中的负荷电流曲线如图6。

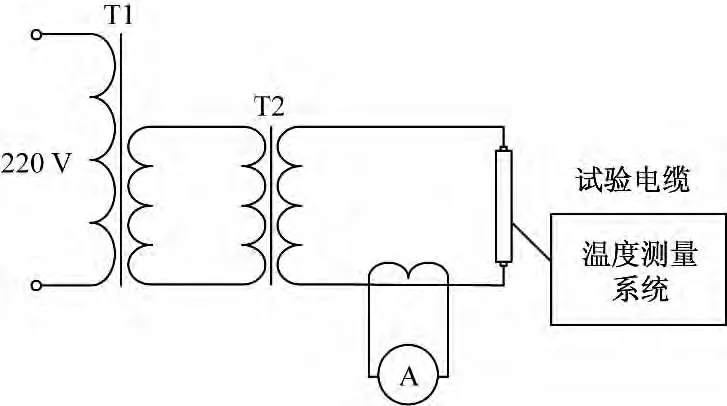
图4 试验电路原理图

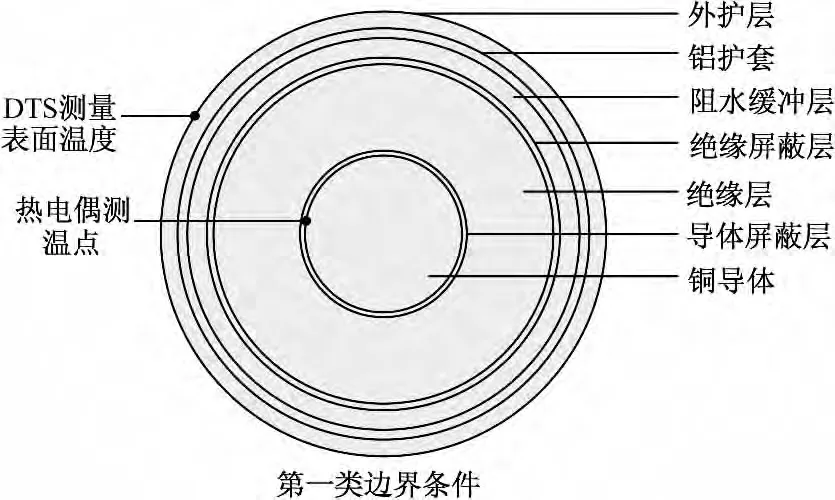
图5 试验电缆结构示意图

图6 负载电流曲线

本次试验测量时间约为8 h，热电偶和DTS的采样周期为60s，总共473组测量数据。图7为DTS所测电缆表面温度，通过曲线可知，电缆表面温度在给定的负荷电流下从7℃上升到36℃。图8为电缆导体温度计算值与测量值的曲线对比图，测量值为3个热电偶在某个时刻的平均值。从图8中可以看出，计算结果与试验结果基本相符，计算误差随着试验时间的增加而略微增大，最小误差为0.001℃，最大误差为2.14℃。

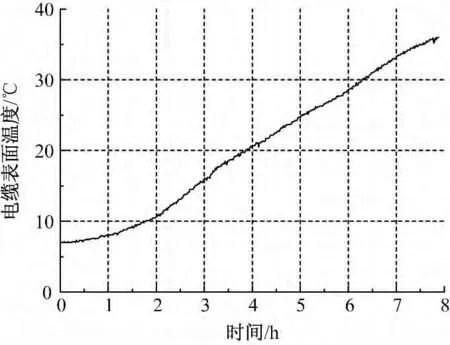
图7 电缆表面温升曲线

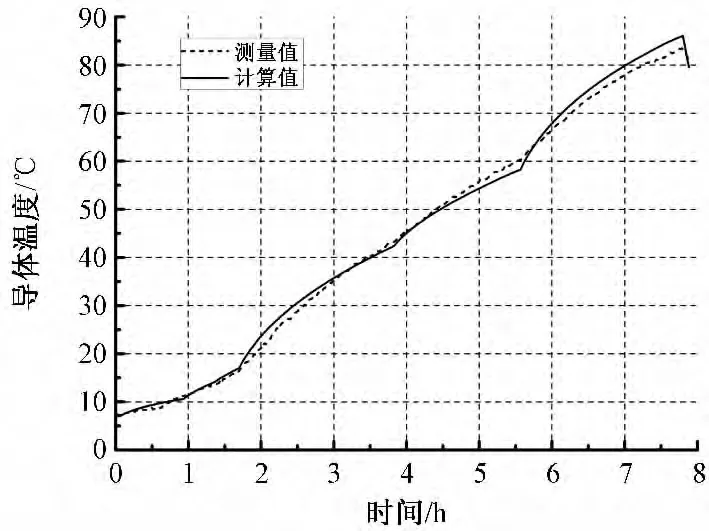
图8 电缆导体温升曲线

分析误差存在的原因，首先一个是测量仪器本身的系统误差导致的:测量电缆导体温度的热电偶和测量电缆表面温度的DTS本身就存在一定的测量误差;热电偶通过绝缘层被插入到导体表面，改变了电缆本身的温度场也会造成误差;此外，用于测量负荷电流的电流互感器也存在测量误差。

其次，计算时使用的电缆结构参数和实际的电缆结构的不一致，电缆导体不是标准的圆柱体，而在计算导体损耗时假设导体为同心圆柱体。此外，计算电缆各部分损耗时使用的IEC经验公式也不可避免地引起计算值和实际情况的误差。

最后一个导致误差的主要因素就是计算时使用的电缆各部分材料的热参数与实际材料特性有一定的差距，计算过程中根据材料类型查表得到材料热参数。由于材料的热参数是随着电缆温度的升高而变化的，另外，电缆缓冲层和皱纹铝套中间会存在微小的空气间隙，这些因素都会导致计算值和实际测量值之间产生误差。

考虑到上述的因素，本文结合DTS测量的电缆表面温度并且利用有限元法计算得到的电缆温度场与试验测量值之间的误差在可接受的范围内。

4 结论

(1)借助于大型通用有限元软件ANSYS，对一根单芯YJLW03 64/110 kV 1×630 mm2XLPE电缆使用三角形单元进行场域剖分。为了提高计算精度而不增加计算时间，对电缆各层的三角形单元尺寸进行了合理的选择，导出剖分区域的单元和结点编号及坐标值信息。

(2)利用有限元基本原理，结合电缆区域剖分信息，建立了电缆区域的温度场计算模型。以DTS测量到的电缆表面温度为第一类边界条件，自主编制程序生成相应的热容、热导及产热矩阵，生成n个代数方程，从而较为精确地得到了整个电缆场域的瞬态温度分布。

(3)对同根YJLW03 64/110 kV 1×630 mm2XLPE电缆开展试验研究。通过电缆导体温升的计算结果与试验测量值的比较，最大误差为2.14℃，验证了使用有限元法计算电缆瞬态温度场的正确性，对于沿表面安装DTS进行实时温度监测的高压或超高压电缆，采用有限元法能够精确地计算出导体的实时温度变化，为电力工程中动态载流量的确定提供了一个比较可靠的计算方法。

［1］李 伟，曾 宏，杨 琳，等.单芯电缆实时载流量计算方法研究［J］.四川电力技术，2011，34(4):61-64.

［2］王东涛，高 丹.基于组态的动力电缆温度在线监测系统［J］.中国电力，2006，39(4):79-82.

［3］IEC 60287-1:2001 Calculation of the current rating-part 1:current rating equations(100%load factor)and calculation of losses［S］.

［4］IEC 60287-2:2001 Calculation of the current rating-part 2:Thermal Resistance［S］.

［5］IEC 60287-3:1999 Calculation of the current rating-part 3:sections on operating conditions［S］.

［6］曹惠玲，王增强，李雯靖，等.坐标组合法对直埋电缆与土壤界面温度场的数值计算［J］.电工技术学报，2003，18(3):59-63.

［7］郑雁翎，许志亮，张冠军，等.采用MATLAB仿真的变电站高压进线温度场和载流量数值计算［J］.高电压技术，2012，38(3):566-572.

［8］梁永春，李彦明，柴进爱，等.地下电缆群稳态温度场和载流量计算新方法［J］.电工技术学报，2007，22(8):185-190.

［9］孟凡凤，李香龙，徐燕飞，等.地下直埋电缆温度场和载流量的数值计算［J］.绝缘材料，2006，39(4):59-61.

［10］梁永春，柴进爱，李彦明，等.基于FEM的直埋电缆载流量与外部环境关系的计算［J］.电工电能新技术，2007，26(4):10-13.

［11］Li H J，Tan K C，Su Qi.Assessment of underground cable ratings based on distributed temperature sensing［J］.IEEE Transactions on Power Delivery，2006，21(4):1763-1769.

［12］王有元，陈仁刚，陈伟根，等.基于有限元法的XLPE电缆载流量计算及其影响因素分析［J］.重庆大学学报，2010，33(5):72-77.

［13］张洪麟，唐 军，陈伟根，等.基于有限元法的地下电缆群温度场及载流量的仿真计算［J］.高压电器，2010，46(2):42-51.

［14］付永长，张文斌，陈 涛，等.不规则排列电缆温度场及载流量计算［J］.电网技术，2010，34(4):173-176.

［15］孔祥谦.有限单元法在传热学中的应用［M］.北京:科学出版社，1998.