线圈转移对导电弹性针织柔性传感器的电学性能影响

王金凤，龙海如

(东华大学纺织学院，上海 201620)

近年来，导电针织物由于其独特的性能和组织结构已在可穿戴式传感器中受到高度重视［1］。针织物的线圈结构使其相对于机织物和编织物来说更加柔软舒适。导电织物传感器是基于外界刺激引起其电阻变化这种原理设计的，这些刺激包括变形、温度、湿度以及某些化学物质。因而针织物受力后的形状变化对穿戴式传感器的设计极其重要。Lord Kelvin［2］于1856年首次发现导电织物的应变变化可引起电阻变化。基于传感器特殊的电力学性能，已设计出线状、箔状等电阻应变计并得到了广泛应用。由古人发明的用于遮羞保暖的纺织品，经过人们不断地创新，已在智能材料［3］中担当重要的角色。

通过分析简单组织结构织物的电阻和张力之间关系可确立传感器的关键因素，如灵敏度、重复性和线性度。综合利用合适的材料和适宜的织物结构可显著改善传感器的这些性能。有文献［4-6］已经描述了导电织物电阻和伸长率之间的关系。

针织物的拉伸直接关系到其变形性能，不同的力学模型［7-9］已对此进行阐述。它们大多对纬平针织物通过微观力学性能分析其线圈结构，然而由于分析过程过于复杂，这些模型应用于导电针织物电-力学性能的预测非常有限，特别是当导电弹性针织物受到双向拉伸变形时。本文通过建立导电弹性纬平针织物电阻六角模型来预测其形变和电-力学性能的关系。除电阻和针织物单向伸长的关系外，该模型也被用于模拟电阻和针织物双向变形的关系。

1 电阻六角模型

将已知电压连到导电弹性针织物两端时，它的电阻会随施加在针织物两端张力的变化而变化。由于所用材料的高导电性，针织物的传导机制用1个纯电阻的电路网来模拟。为了模拟针织物的变形，本文建立电阻六角模型来表征导电针织物的结构特征。为简化线圈电路的分析，作如下假设［10-12］：1)纱线长度能够足够好地表述其实际长度;2)织物的变形是均匀的;3)纱线除了交叠处外其他均为直线;4)纱线半径相对于线圈长度的比例不超过4%(实际上是几何要求)。

图1 示出导电纬平针织物的线圈结构和电阻六角模型表示的导电针织物等效电路。1个线圈由圈柱、针编弧和沉降弧［13］组成;其电阻包括2个接触电阻(Rc)和3个纱段电阻(Rl)，分别与相互交叠的纱线接触力和导电纱线的自身电阻有关。2个交叠的纱段接触电阻(Rc)假定只与纱段的正接触力有关，并不考虑它们在交叠区域的接触长度。针编弧和沉降弧长度几乎相同，在图中它们都用Ra表示;圈柱部分用Rb表示。该等效电路可以看作是各纱段电阻和接触电阻组成的串并联复杂电路网。

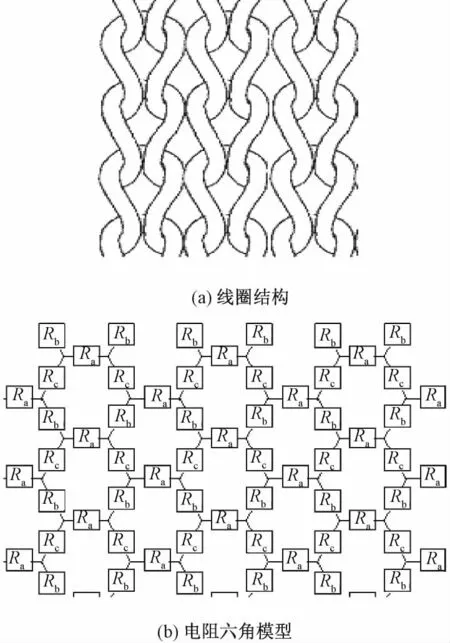
图1 导电纬平针织物结构和电阻六角模型Fig.1 Plain weft knitted fabric structure(a)and resistance hexagonal model(b)

根据基尔霍夫定律求解电路网可以得到针织物的等效电阻。针织物电阻受纱线电阻、线圈纱段转移及纱线间接触电阻3个因素影响。纱线电阻随拉伸应变的增加而增加，这与金属导体电阻定律R=ρl/A相一致，其中，R为电阻，ρ为电阻率，l为纱线长度，A为纱线横截面积。纱线长度和横截面均为拉伸应变的函数;当应变增加时，纱线长度增加，横截面减少，相应地电阻增加。纱线间接触力为拉伸应变的函数，接触电阻与纱线接触力的关系可以从测量拉伸情况下2个弯曲相互钩套在一起的纱线电阻与张力关系的实验中得到。当针织物受力拉伸时，线圈纱线间的接触力随之增加;接触电阻与接触力的关系如经验公式［14］Rc=K所示，其中，Rc为接触电阻，Fc为接触力，K为与材料相关的常数，m为与接触状态相关的常数。由于导电纱线间是圆柱与圆柱的接触，从而选择m=0.5。经研究可得，接触电阻随接触力的增加成幂函数减小，接触力随拉伸张力的增加而增加，从而接触电阻随拉伸张力的增加而减小。本文着重分析线圈转移对针织物电阻的影响。

2 线圈纱段转移的影响

2.1 拉伸状态下的针织物电阻

当针织物受到平行于横列的单方向拉伸张力时，线圈结构将发生变化，圈柱纱段将会向针编弧和沉降弧纱段转移，从而圈柱部分的纱线长度会减小，针编弧和沉降弧部分的纱线长度会增大。最后，纱线将沿自身轴线方向拉直。同时，在伸长过程中纱线间接触力增加。

针织物的拉伸变形过程分为以下几个步骤：第1步，弯曲部分纱段拉伸成直线;第2步，直线部分开始伸长。此外，下列现象伴随这些步骤：1)在纱线交叠处纱线滑移;2)在交叠处纱线存在挤压变形。

在针织物实际变形过程中这2个步骤是同时进行的，但为了简化分析，把这2个步骤分开。理想的拉伸状态下，弯曲纱段只会伸直而没有沿纱轴方向的伸长。对于导电弹性纬平针织物，在小应变变形时，单元线圈纱线间接触力变化很小，从而接触力对针织物在拉伸情况下电阻的影响可以忽略不计。图2为只考虑线圈转移而不考虑接触电阻，对导电针织物拉伸情况下建立的电路模型。

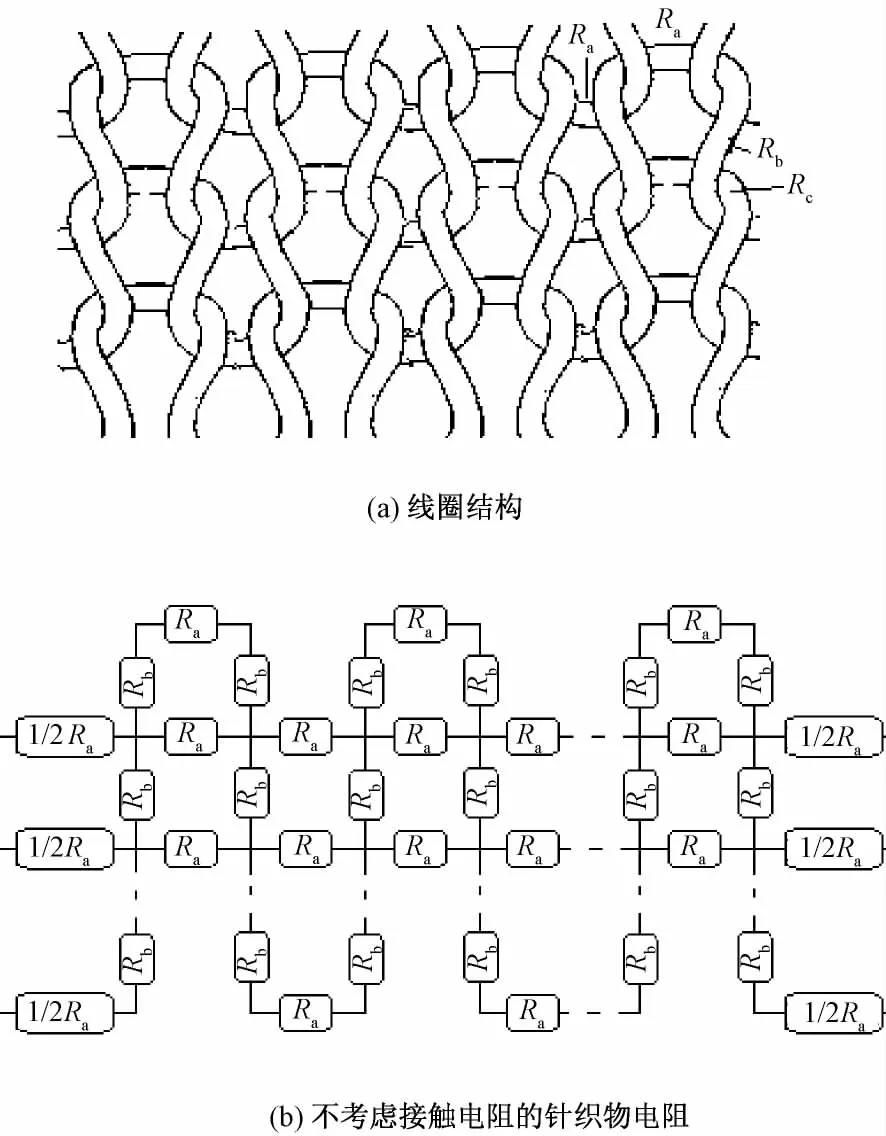
图2 线圈结构及不考虑接触电阻的纬平针织物电阻Fig.2 Plain weft knitted fabric structure(a)and resistance without considering Rc

本文从2横列×1纵行线圈到m横列×n纵行线圈分析不同横列、不同纵列线圈的整个针织物电路网。采用基尔霍夫电压定律和回路电流法来计算导电针织物电路的总电流I1。基尔霍夫电压定律，简记为KVL，是确定电路中任意回路内各电压之间关系的定律，因此又称为回路电压定律，它的内容为：在任一瞬间，沿电路中的任一回路绕行1周，在该回路上电动势之和恒等于各电阻上的电压降之和。它说明任一回路中所有支路电压的代数和等于零。回路电流法，以回路电流为未知量，根据KVL列出独立回路的电压方程，联立求解的方法。电路的简化遵循这2个定律［15］，一般为Y形联结与△形联结的等效变换(见图3)。

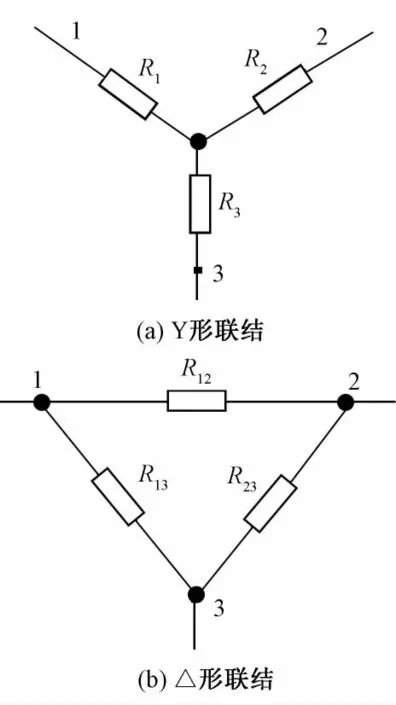
图3 Y形联结与△形联结的等效变换Fig.3 Equivalence transformation between Y(a)to△(b)connected circuit

根据Y形联结的电阻确定△形联结的电阻公式为

根据△形联结的电阻确定Y形联结的电阻公式为

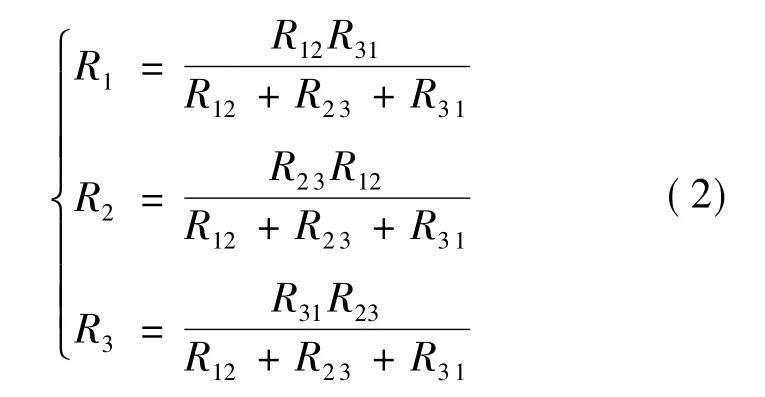
2.2 m×n个线圈针织物

所有的线圈电阻电路均按上文的方法进行分析，本文先从2横列×1纵行线圈针织物开始(见图4)。

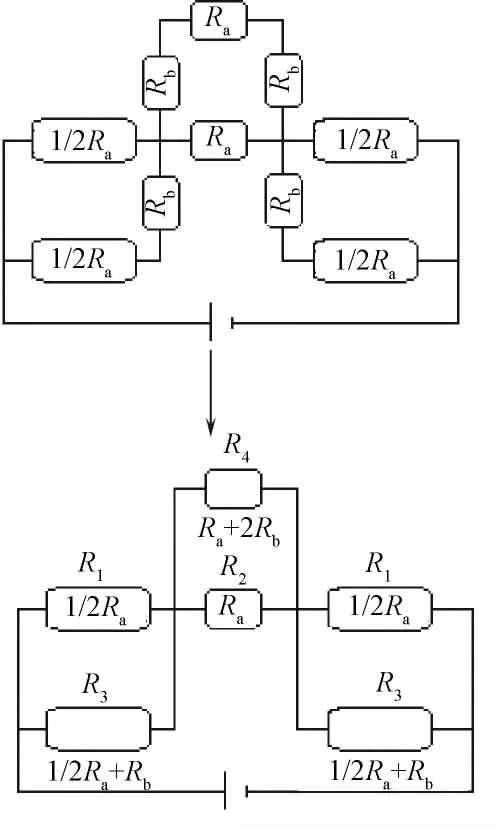
图4 2横列×1纵行线圈针织物电阻Fig.4 Resistance of 2 wales×1 course unit loops knitted fabric

如果将针织物两端加载电源，其电压为U，电路可简化为先分别2个电阻并联，然后各电阻间串联的等效电阻，如式(3)所示。

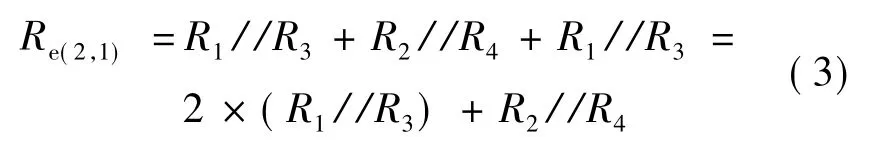
相同端点2个电阻并联等效电阻分别为

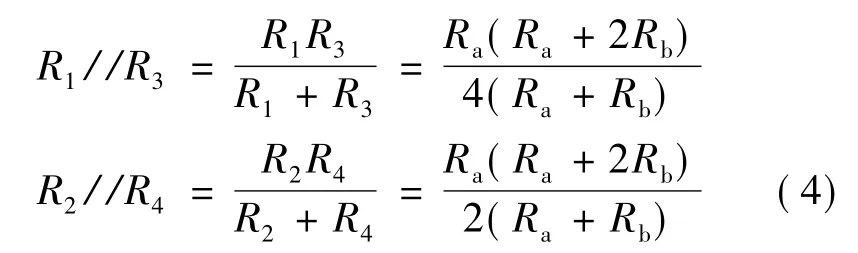
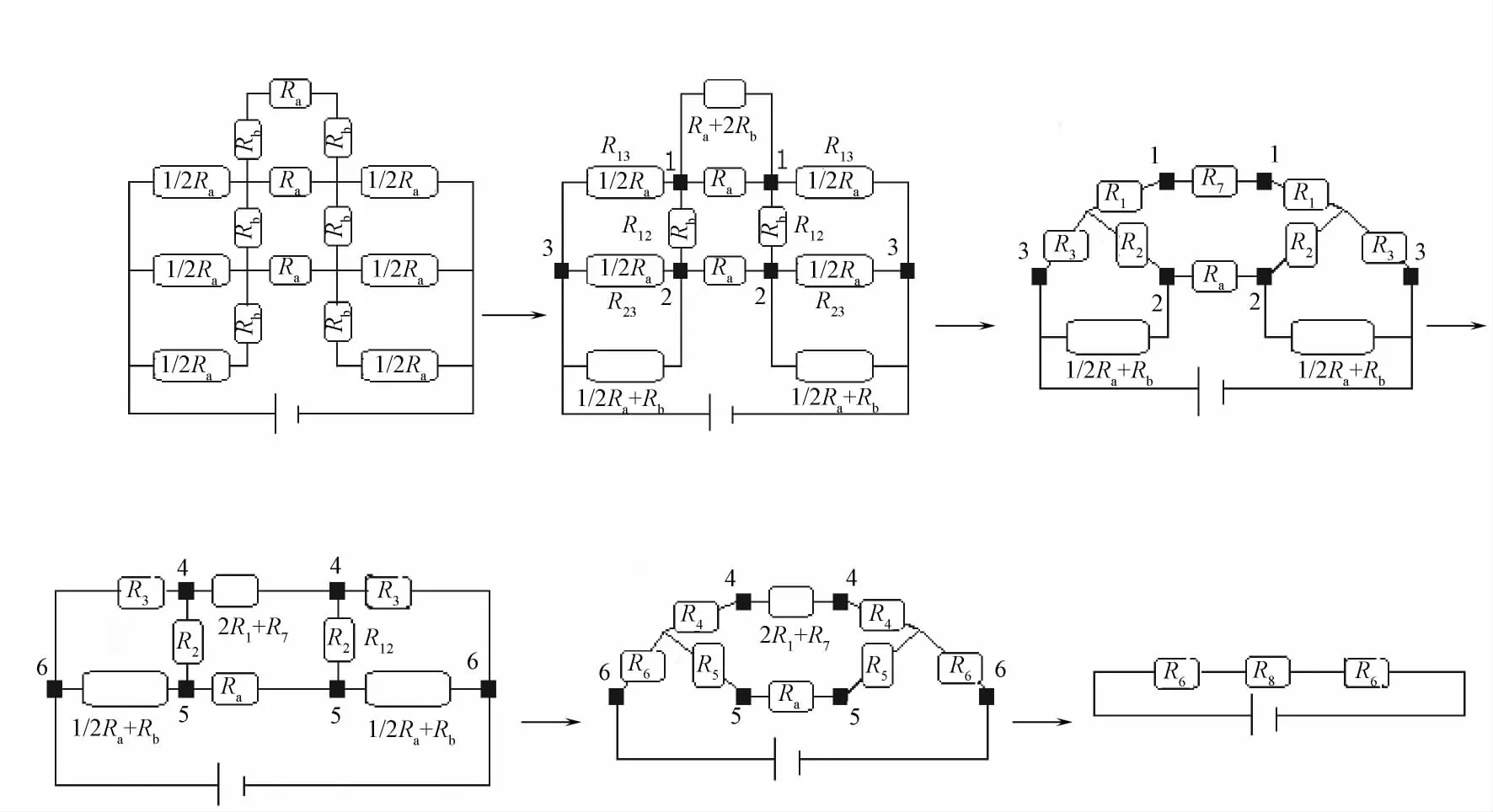
图5 3横列×1纵行线圈针织物电阻Fig.5 Resistance of 3 wales×1 course unit loops knitted fabric

电路等效电阻为

同样的方法可以求得2横列×2纵行和2横列×3纵行线圈针织物的等效电阻，分别用式(6)和式(7)表示。

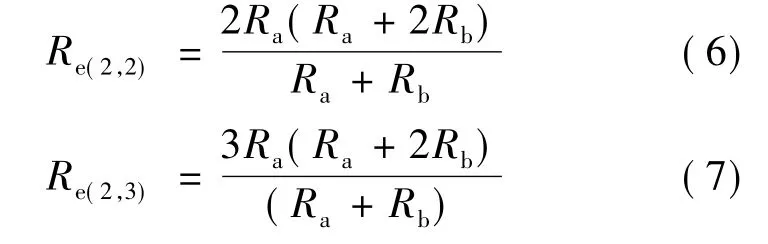
对3横列×1纵行线圈针织物的电阻进行多次△形联结与Y形联结的等效变换来简化电路，利用MatLab软件可以求解等效电阻，可得图5及式(8)。

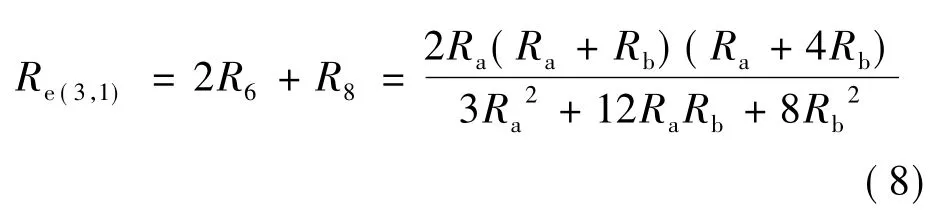
同样的方法可求得3横列×n纵行和4横列×n纵行线圈织物的等效电阻，如表1所示。

从表1可看出：沿导电针织物的纵行方向，其电路为并联电路，电阻随横列数的增加而减小;沿导电针织物的横列方向，其电路为串联电路，电阻随纵行数的增加而增加。为了简化计算过程，只需计算m横列×1纵行线圈针织物的电阻值，如式(9)所示。

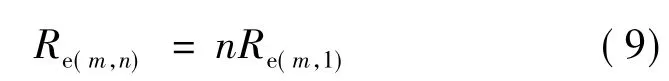
表1 各种横列纵行针织物电阻表达式Tab.1 Resistance expressions of all kinds of unit loops

本文采用的针织物试样是由锦/氨包芯纱为地纱、锦纶镀银纱为添纱编织而成。锦纶镀银纱的电阻是0.516 Ω/mm，试样的线圈长度(l)是3.55 mm，圈距(w)是0.65 mm，圈高(c)是0.45 mm。针织物由20横列和60纵列线圈组成，如图6所示。

图6 镀银纱弹性平纹针织物Fig.6 Silver-plating yarn elastic knitted plain fabric

试样的电阻值用万用电表测量，结果如表2所示。从表2可得到式(10)，由此验证了式(9)正确。

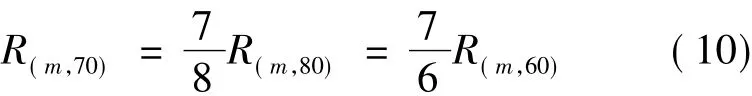
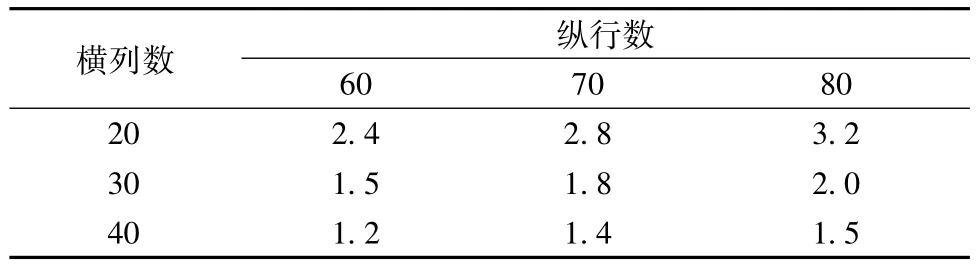
表2 针织物电阻实测值Tab.2 Resistances of samples Ω

2.3 试样电阻与应变的关系

假设单元线圈长度是常数，不会因针织物的拉伸变形而变化。线圈长度用式(11)［10］计算。

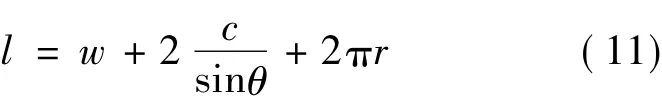
式中：r是纱线半径，θ是圈柱与水平方向的角度。假设针编弧(沉降弧)长度Ra0=0.167 7 Ω，Rb0=0.748 2 Ω。

假设2横列×1纵行、3横列×1纵行、4横列×1纵行线圈针织物受平行于横列的拉伸张力(ε=5%)，la由式la=la0(1+ε)求得，从而 lb、Ra、Rb可以求得。针织物等效电阻可以由表1求解，分别用方点、三角点分布表示;用MatLab软件对等效电阻计算值做线性回归，分别用实线表示。图7示出各针织物等效电阻的表达式。即使各不相同，但是都随应变的增加而线性增加，并随横列数的增加而减小。

图7 计算和模拟的等效电阻曲线Fig 7 Equivalent resistances calculated and fitting curves

当针织物拉伸应变在5%以内时，电阻几乎是线性增长的，所以本文用线性方程来模拟，见图8。图中方点、三角分布为实测数据，实线是由MatLab软件拟合所得曲线。图中显示：不同横列数、相同纵行数线圈的针织物电阻有相同的增长趋势;此趋势与图7相同。由此可以验证此结果符合本文的模型。当针织物受到小应变拉伸下，线圈纱段转移在针织物电阻中发挥着重要作用。

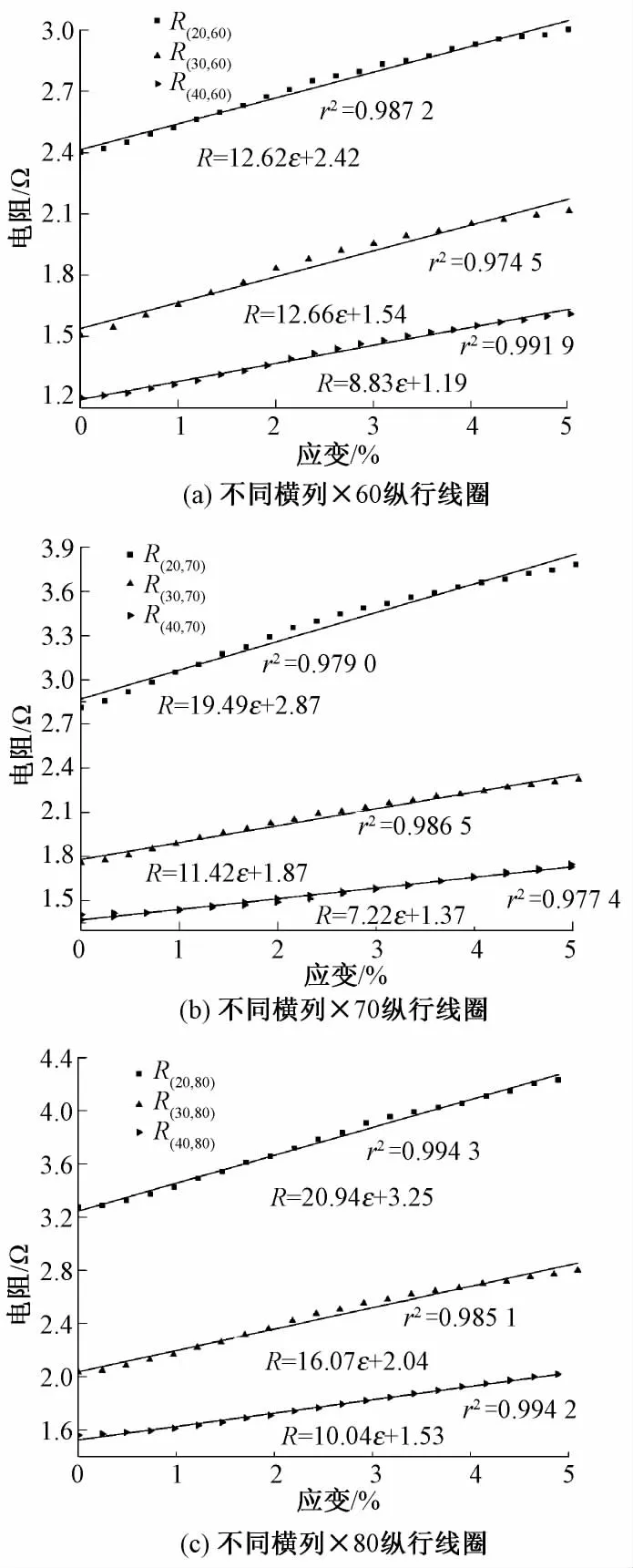
图8 在5%应变内针织物电阻与应变的关系Fig.8 Resistance vs.strain within 5%.(a)60 wales by different courses;(b)70 wales by different courses;(c)80 wales by different courses

3 结论

基于导电弹性纬平针织物的线圈结构建立电阻六角模型，利用基尔霍夫电压定律和电流回路定律求解针织物等效电阻，用以模拟传感器的传感机制和验证其可靠性。其等效电阻和拉伸应变的关系由计算机程序模拟。针织物电路是综合串联和并联的复杂电路网;沿纵行方向，它是一个并联电路;沿横列方向，它是一个串联电路。为简化计算过程，只需计算m横列×1纵行线圈的等效电阻。

线圈纱段转移引起了弹性针织物柔性传感器的电阻变化，并且是影响传感器灵敏度的关键因素;针织物电阻随应变的增加而线性增加。研究发现：模拟结果与实验数据基本一致。为了改善针织物传感器的灵敏度，提高线圈纱段转移引起的电阻变化与拉伸应变的线性度是非常重要的;此外，接触电阻、织物结构和纱线伸长也影响针织物传感器的性能。

［1］DE RossiD， DELLA SantaA， MAZZOLDIA.Dressware：wearable hardware［J］.Materials Science and Engineering：C，1999，7(1)：31-35.

［2］THOMSON W.On the electro-dynamic qualities of metals-effects of magnetization on the electric conductivity of nickel and of iron［C］//Proceedings of the Royal Society of London.1857：546-550.

［3］TAO Xiaoming.Smart Fibres，Fabrics and Clothing：Fundamentalsand Applications［M］.Cambridge：Woodhead Publishing，2001：200-220

［4］GREGORY R V，KIMBRELL W C，KUHN H H.Conductive textiles［J］.Synthetic Metals， 1989，28(1/2)：823-835.

［5］KUHN H H，KIMBRELL W C，WORRELLg，et al.Properties of polypyrrole treated textile for advanced applications［C］//Proceedings of the Society of Plastics Engineers' 49th Annual Technical Conference(ANTEC).Montreal，1991：760-764.

［6］OH K W，PARK H J，KIM S H.Stretchable conductive fabric for electrotherapy［J］.Journal of Applied Polymer Science，2003，88(5)：1225-1229.

［7］SHANAHAN W J，POSTLE R A.Theoretical analysis the tensile properties of plain-knitted fabrics：part Ⅰ：the load-extension curve for fabric extension parallel to the course［J］.Journal of the Textile Institute，1974，65(4)：200-212.

［8］WHITENEY J M，EPTING J L.Three-dimensional analysis of a plain knitted fabric subjected to biaxial stresses［J］.Textile Research Journal，1996，36(2)：143-147.

［9］MACRORY Brian M，MCNAMARA Aidan B.Knitted fabrics subjected to biaxial stress：an experimental study［J］.Textile Research Journal，1967，37(10)：908-911.

［10］POPPER Peter.The theoretical behavior of a knitted fabric subjected to biaxial stresses［J］.Textile Research Journal，1966，36(2)：148-157.

［11］HEPWORTH Barbara.The biaxialload-extension behavior of a mode of plain weft-knitting：partⅠ［J］.Journal of the Textile Institute，1978，69(4)：101-107.

［12］KAWABATA S.Nonlinear Mechanics of Woven and Knitted Materials［M］//Textile Structural Composites：Chapter 3.CHOU T W，KO Frank K.Textile Structure Composites.Amsterdam：Elsevier，1989：67-116.

［13］龙海如.针织学［M］.北京：中国纺织出版社，2008：1-15.LONG Hairu.Knitting［M］.Beijing：China Textile ＆Apparel Press，2008：1-15.

［14］HOLM Ragnar.Electric Contacts［M］.4th ed.New York：Springer-Verlag，Berlin，1967：7-19.

［15］邱关源.电路［M］.北京：高等教育出版社，2006：51-64.QIU Guanyuan.Circuit［M］.Beijing： Higher Education Press，2006：51-64.