光晶格动量依赖偶极势中原子运动

余学才 汪平和 张利勋

(电子科技大学光电信息学院,成都 610054)

(2013年1月25日收到;2013年3月29日收到修改稿)

1 引言

近二十年来,中性原子激光导引、冷却和操作的迅速发展开辟了原子光学学科[1-3].置于激光场中的中性原子,在共振或近共振相互作用下,主要受到两个力的作用.一个力是源于自发辐射的辐射力,另一个力是原子偶极矩受光场的作用力,后者正比于光场的空间梯度.在驻波激光场中,驻波激光场形成一个1维或2维的空间周期势晶格.偶极力用于原子导波[4-9]、原子束折射、反射、聚焦[10-13]和分束[14-19].由于偶极势可以通过调制激光束得到控制,偶极势提供了一个控制玻色凝聚体的有效手段.光晶格势场中不存在晶格热振动、晶格缺陷等现象,被光晶格囚禁的玻色原子云可望保持很好的量子相干性.对于原子操作,可以增加失谐将辐射力降低到可以忽略的程度,此时原子主要受偶极力的作用.

由于多普勒效应,光场作用下原子偶极势既依赖于空间坐标,也依赖于原子的动量.原子在这个独特的动量依赖势场中的运动令人迷惑.对原子在偶极力中的运动,已做了相当多的研究,文献[1,20,21]对这些理论和实验研究做了总结.在这些研究中,偶极力的动量依赖特性未予考虑.但文献[8]根据偶极力的动量依赖特性提出了一种消色差的原子透镜.在本文中,我们考虑了偶极力的动量依赖特性,研究了红失谐下光晶格势场中原子的动量演化.结果表明,初始动量较大的原子,飞入光晶格势场中后,动量演化可以分为三个阶段.在第一阶段,原子动量缓慢减小.原子动量在光晶格的第一半周期减小,下半周期增加,但原子飞跃一个晶格后动量有一个很小的净减小量.这个结果和以前研究原子在偶极力中减速的结果一样,文献用希腊神话中的西西福斯(Sisyphus)神从山脚到山顶永无止境滚石的过程来类比这个过程[22-24].第二阶段,当原子飞跃很多个晶格后,原子动量减小到光子动量时,会很快下降.第三阶段,原子动量在波腹和波节分别达到如下极限：

式中h¯k是光子动量,Ω是拉比频率,γ为原子波函数的时间衰减常数.在其他位置,原子的动量在上述两个数值之间.由于一般情况下拉比频率远小于波函数衰减常数(Ω≪γ),所以原子动量极限远小于光子动量.在第三阶段,如果有很多原子进入光晶格,原子将逐渐在波腹处和波腹附近积累起来,形成捕获原子云.对动量和位置的方差计算表明,原子动量呈现压缩性质,位置呈现放大性质.因此,在红失谐动量依赖光学偶极力作用下,原子最终量子态可能接近于动量压缩线态(line state).此结论表明,文献[25,26]关于外势场中玻色气体在零动量态上凝聚的假设应为动量压缩线态上凝聚.

2 运动方程

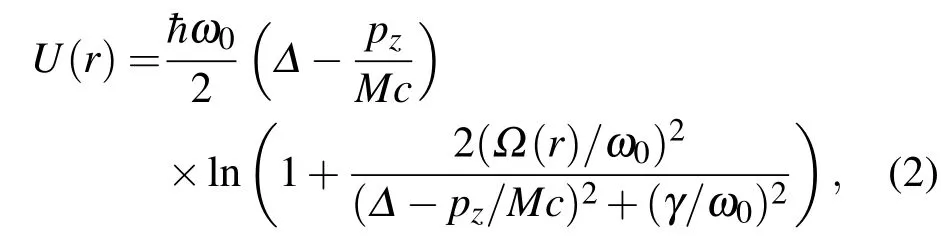
早在1978年,Ashkin[27]就导出了在非饱和情况下,连续波和原子近共振相互作用偶极势为其中M为原子质量,c为光速,pz为光传播方向上的原子动量,为拉比频率,Δ=(ω-ω)/ω 为失谐量.由于拉比频率一般00情况下远小于原子频率(Ω≪ω0),方程(2)后来被广泛用于原子激光操作实验和理论研究中[24].其中第一个因子反映了偶极势与失谐的关系,在红失谐下势场为负,蓝失谐下势场为正;第二个因子反映了势场和拉比频率的依赖关系,拉比频率越高,势场绝对值越大.在驻波情(况下,偶)极势可近似为

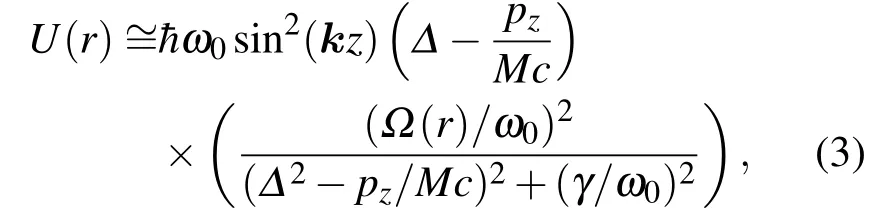
其中k为波矢.此势包含了一个空间周期函数sin2(k z)和一个动量依赖函数 f(pz).原子的哈密顿量为

经过一系列复杂精密对易关系计算(附录),动量和位置运动方程分别为

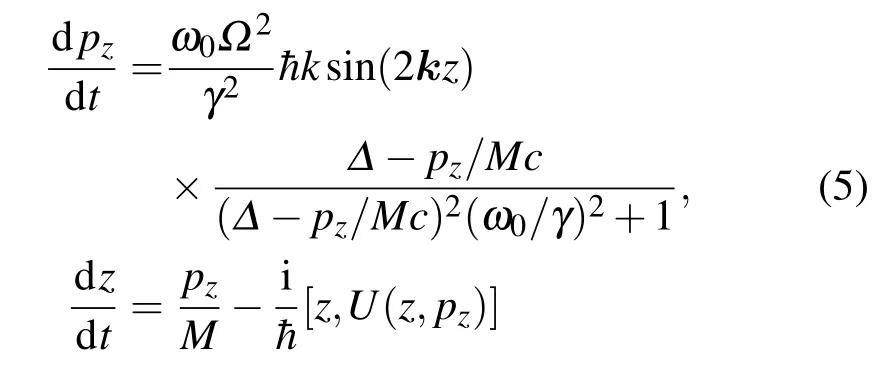
(6)式中右边第二项来源于势动量依赖函数.与不依赖于动量的运动方程d p/d t比较,此项是考虑了动量依赖关系后增加的.后面的计算结论表明,此项决定了极端慢速原子的行为.将动量、时间和位置做归一化为无量纲物理量：

运动方程变为

通过稳态条件d p/d t=dφ/d t=0得到动量的最终极限(1)式.但是只有在波腹和波节能够达到稳态条件,在其他位置,动量值在(1)式给出的两个值之间.当失谐量满足|ω-ω0|≪γ,动量在波腹处的极限值为h¯ k(Ω/γ)2.在小信号(非饱和)条件下,由于拉比频率远小于能级衰减常数(Ω/γ≪1),所以原子的动量极限远小于光子动量.

3 动量演化

考虑较大动量

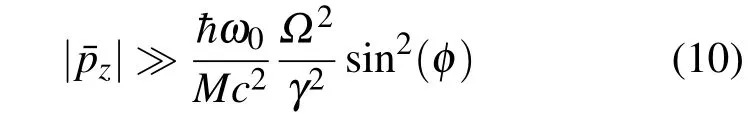
情况,运动方程可近似为

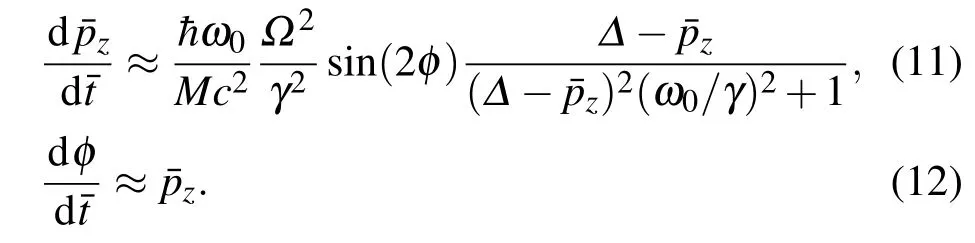
对方程(11)和(12)数值求解,结果如图1所示,动量近似阻尼振荡.在原子飞跃一个晶格期间,第一半周期原子被减速,第二半周期原子被加速.飞跃一个晶格后,动量有一个很小的净减小量：

p¯z,j代表原子进入第j个晶格时的动量.如果p¯z,j小于失谐量,动量净变化小于0,原子被减速;反之,原子被加速.所以原子被加速还是减速不仅决定于是红失谐还是蓝失谐,还取决于原子的初始动量.在红失谐条件下(Δ＞0),归一化动量小于失谐量的原子被减速;归一化动量大于失谐量的原子则被加.原子飞跃第j个晶格的时间Δt¯j近似为

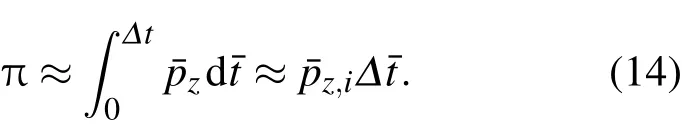
图1 原子在初始几个光晶格中的动量演化,原子在一个晶格的第一半周期被加速,第二半周期被减速.经过一个晶格后,原子动量有一个净减小量(初始动量¯p0=10-6,相当于初始速300 m/s,失谐量Δ=10-12,ω0/γ=105,¯hω0/Mc2=10-9,拉比频率Ω/γ=10-1)

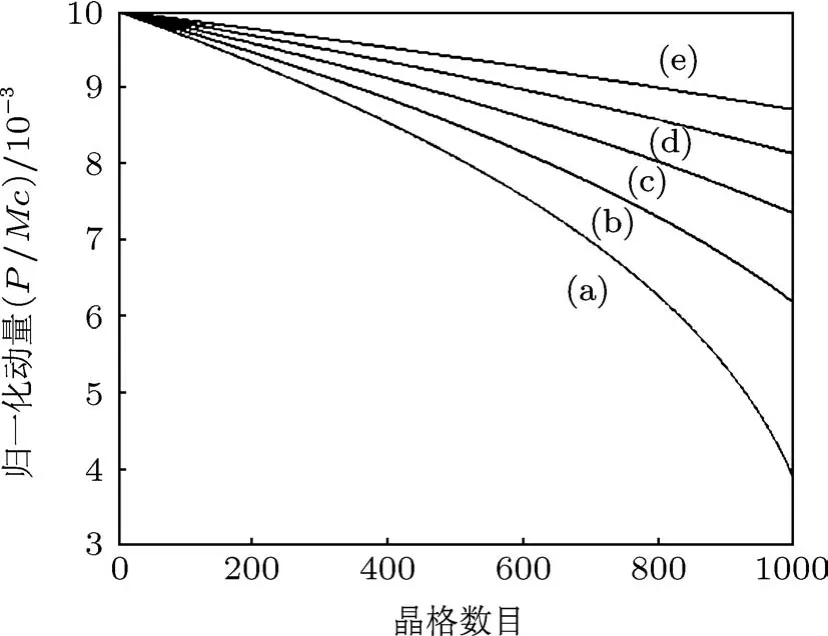
图2 不同拉比频率下原子飞跃1000个晶格的动量净减小量(拉比频率Ω/γ：(a)0.1,(b)0.09,(c)0.08,(d)0.07,(e)0.06;初始速度300 m/s,失谐量Δ=10-6,¯hω0/Mc2=10-9,ω0/γ=105)

图2 和图3分别给出不同拉比频率和初始动量下动量减速的情况.需要飞跃很多个晶格后动量才能有效降低.当动量减小到¯hk量级时,动量急剧下降(图4),迅速达到最终极限(图5),在波节和波腹处达到(1)式给出的值.在此期间,如果有大量原子入射,原子将在波腹和波腹附近逐渐积聚.

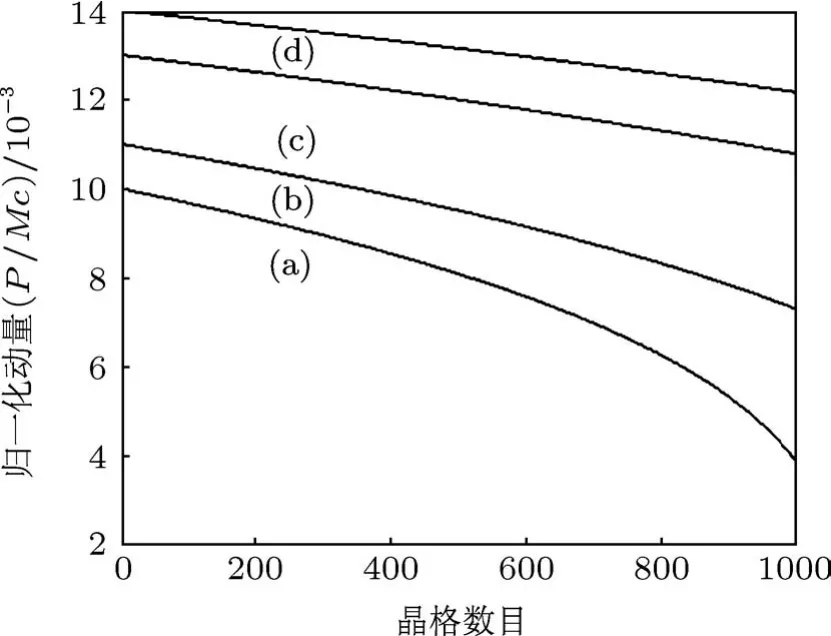
图3 不同初始动量下原子飞跃1000个晶格的动量净减小量(初始动量¯p0：(a)10-2,(b)1.1×10-2,(c)1.3×10-2,(d)1.4×10-2;拉比频率Ω/γ=0.1,失谐量Δ=10-6,¯hω0/Mc2=10-9,ω0/γ=105)

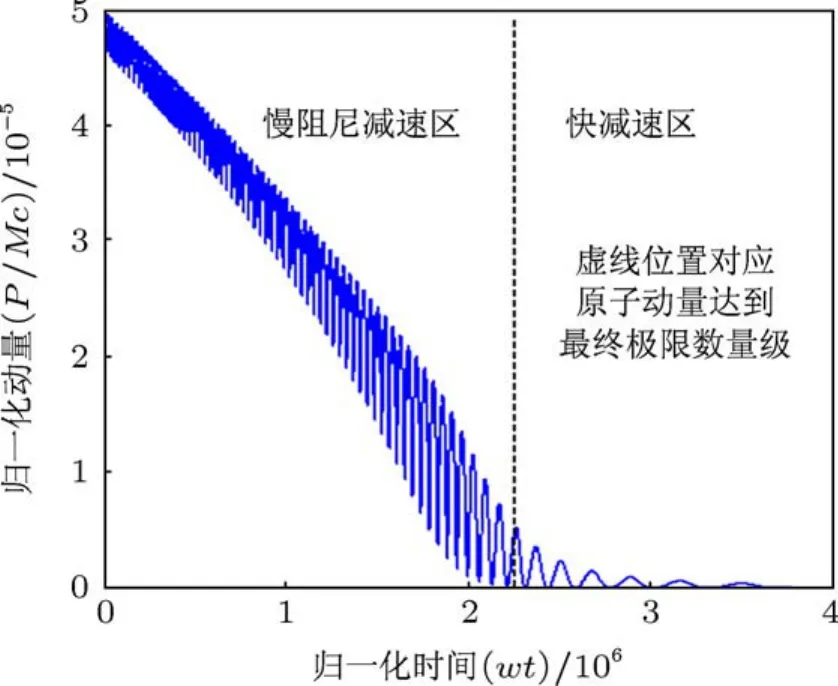
图4 动量演化的全貌 经过较长时间的减速后,动量接近¯hk(Ω/γ)2量级时,原子迅速减速原子,并逐渐停止在波腹和波腹附近处(初始动量¯p0=5×10-5,失谐量Δ=10-12,拉比频率Ω/γ=0.3,¯hω0/Mc2=10-9,ω0/γ=105)

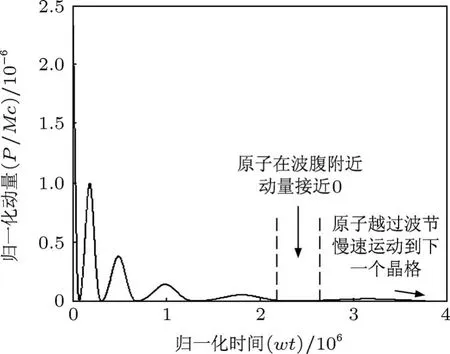
图5 原子动量在达到极限时的较详细情况 原子在波腹和波腹附近动量接近0,但加速度不为0,因此缓慢越过波节运动到下一个晶格(初始动量¯p0=2.5×10-6,失谐量Δ=10-12,拉比频率Ω/γ=0.5,¯hω0/Mc2=10-9,ω0/γ=105)

4 动量压缩性质

原子在光晶格中经过很长时间的飞行⟨后,⟩经历了一个各态历经的过程,我们用时间平均p2z=代替海森伯绘景下量子平均求动量和位置的方差：

结果如图6和图7所示.从图中可见,动量方差经过一个最大值后缓慢减小,位置方差则单调增加.因为各态只有经历足够长的时间后才可能是正确的,时间较短的平均值是不可信的,所以动量方差最大值之前的单调上升的趋势是不可信的.在经过近十万个光学周期(微秒时间)后,动量方差单调减小,说明了原子在一个动量减速势中经过较长时间后处于动量压缩态的性质.

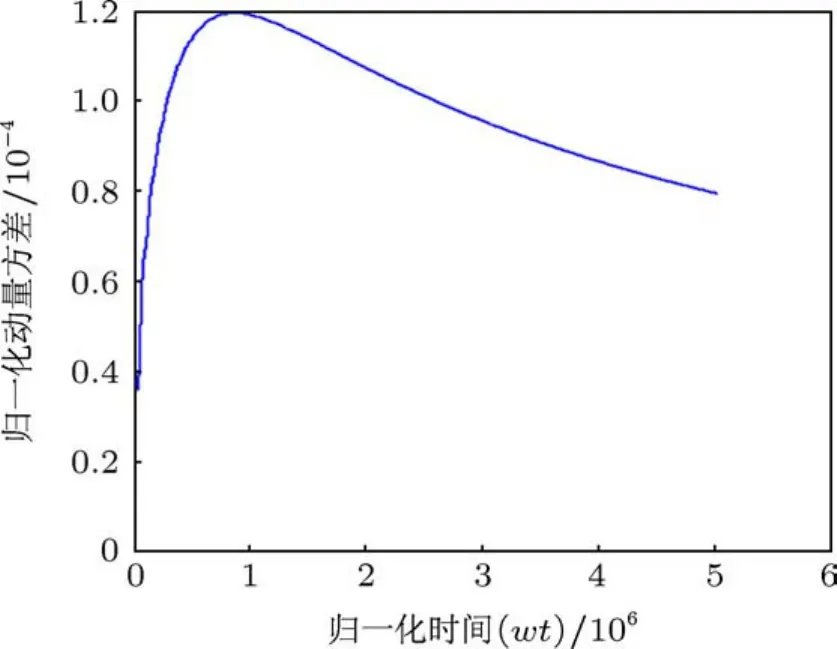
图6 归一化动量方差(初始动量¯p0=1.25×10-5,拉比频率Ω/γ=0.1,失谐量Δ=10-8,¯hω0/Mc2=10-9,ω0/γ=105)

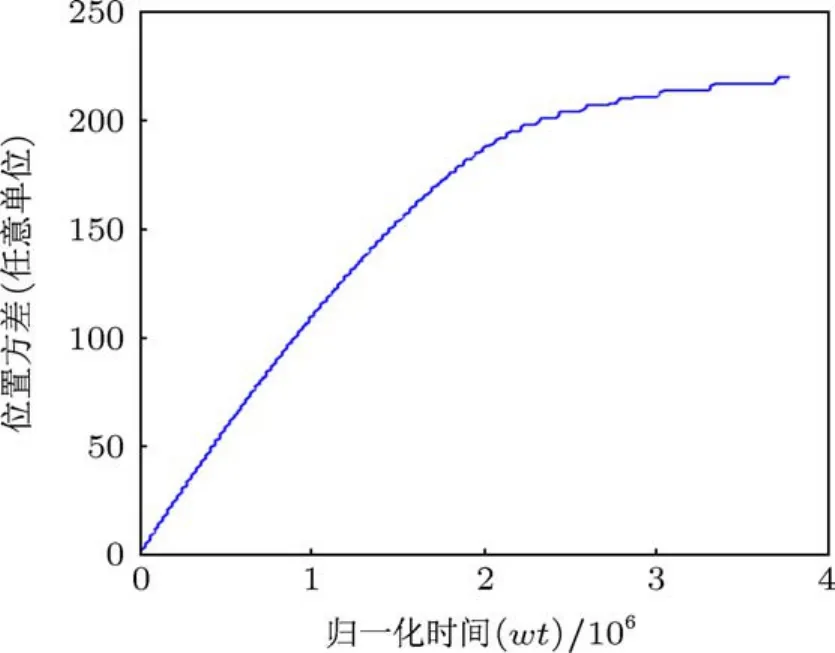
图7 归一化位置方差(初始动量¯p0=1.25×10-5,拉比频率Ω/γ=0.1,失谐量Δ=10-8,¯hω0/Mc2=10-9,ω0/γ=105)

5 高斯晶格下原子运动

考虑高斯光束构成的晶格,拉比频率为

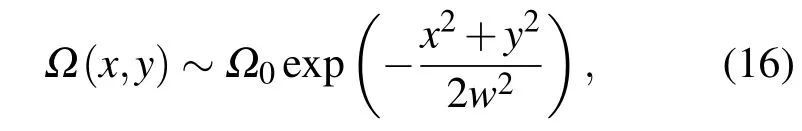
其中w为光斑半径.原子的运动轨道由下面方程求出

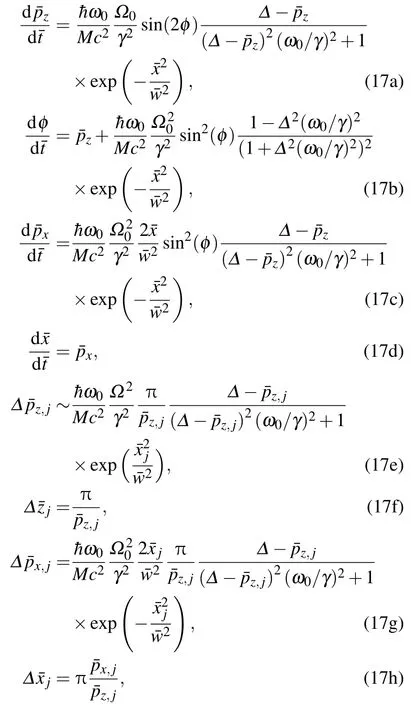
式中p¯x=px/Mc,x¯=kx,w¯=kw.图8和图9分别给出了原子在不同横向动量下和不同拉比频率下的运动轨道.横向向外运动的原子,横向动量较小的情况下,将被偶极势拉回到光束中心,原子轨道对拉比频率十分敏感.拉比频率越大,原子越容易被拉回到光束中心.

6 结果与讨论

本文研究了光晶格势中原子的动量演化,特别考虑了偶极势的动量依赖关系.对动量和位置的方差计算表明,原子动量呈现压缩性质,位置则呈现放大性质.根据此结论,我们预言光晶格动量依赖偶极势中的单粒子态可能接近动量压缩线态.研究结果表明,原子动量演化可以分为三个过程：第一个过程是阻尼振荡衰减过程,此过程对初始动量较大的原子,将持续很长的时间;第二个过程是当动量被降低到光子动量数量级时,动量急速减小;第三个过程是原子逐渐在波腹与波腹附近停下来,被囚禁在波腹附近.

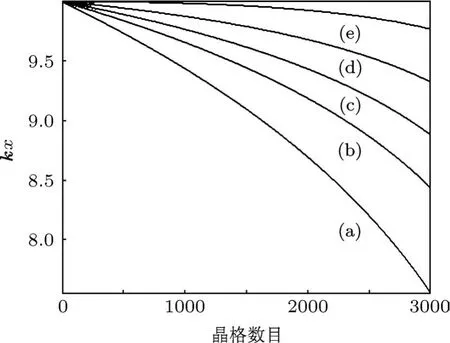
图8 不同初始横向动量下原子轨道初始横向动量¯p：(a)-8×10-9,(b)-6×10-9,(c)-4×10-9,(d)-2×10-9,(e)0;拉比频率Ω/γ=0.1,失谐量Δ=10-8,初始纵向动量¯pz=10-5,初始横向位置x=10λ,光斑半径w=100λ,¯hω0/Mc2=10-9,ω0/γ=105

图9 不同拉比频率下原子轨道 Ω/γ：(a)0.12,(b)0.11,(c)0.1;初始向外横向动量¯px=2×10-9,失谐量Δ=10-8,初始纵向动量¯pz=10-5,初始横向位置x=10λ,光斑半w=100λ,¯hω0/Mc2=10-9,ω0/γ=105

本文推导了海森伯绘景下依赖于动量偶极势中原子运动方程,是全量子理论,可用于进一步研究原子激光束聚焦、原子激光捕获以及原子激光束反射镜等效应.

附录

动量方程：

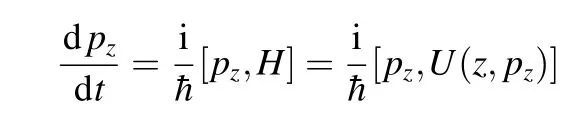
式中p0=McΔ.从对易关系

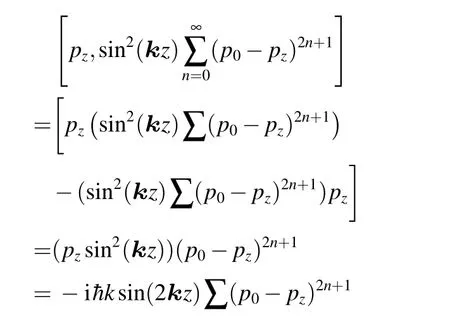
得到：

位置方程：

计算对易关系：

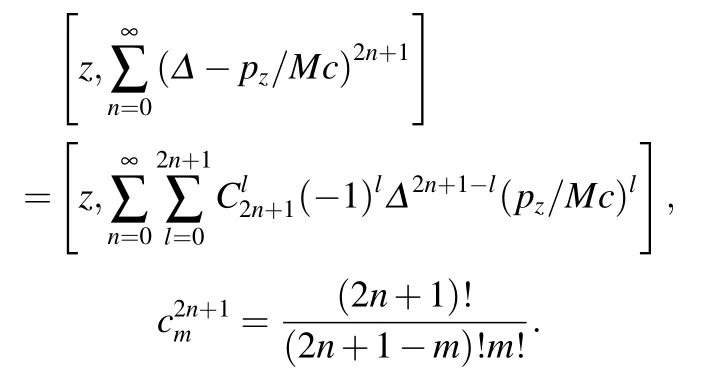
利用：

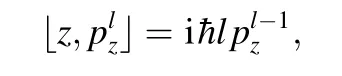
得到：

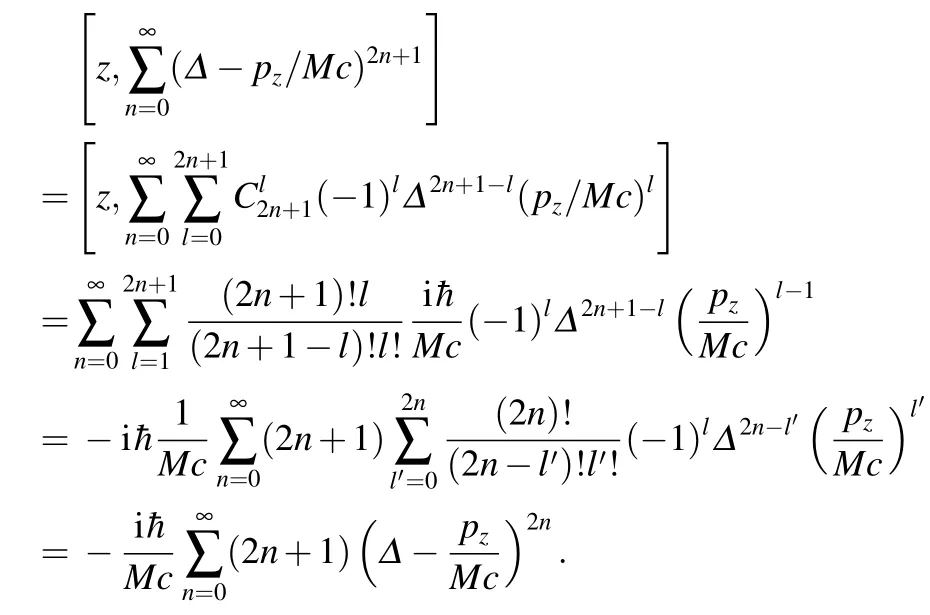
再利用求和公式：

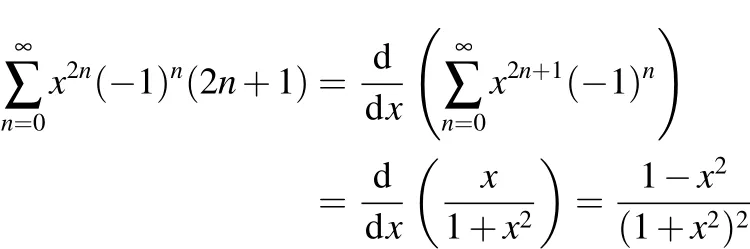
最后得到：

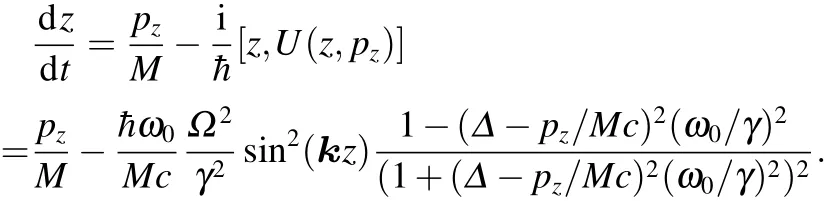
[1]Grynberg G,Robilliard C 2001 Phys.Rep.355 335

[2]Balkin V I 1989 Phys.Today 42 23

[3]Meystre P2001 Atom Optics(Berlin：Springer Verlag)

[4]Renn M J,Montgomery D,Vdovin O 1995 Phys.Rev.Lett.75 3253

[5]Cook RJ,Hill RK 1982 Opt.Commun.43 758

[6]Olshanii M A,Ovchinnikov Y B,Letokhov V S 1993 Opt.Commun.98 77

[7]Marksteiner S,Savage CM,Zoller P1994 Phys.Rev.A 50 2680

[8]Drewsen M,Spreeuw RJC,Mlynek J1996 Opt.Commun.125 77

[9]Lanurence PD,Olivier H,Hong T D 1999 Opt.Commun.166 199

[10]Helseth L E 2002 Opt.Commun.212 343

[11]Helseth L E 2001 Opt.Commun.191 161

[12]Yougworth K S,Brown T G 2001 Opt.Express7 77

[13]Biss D P,Brown T G 2001 Opt.Express9 490

[14]Olivier H,Demascoth K,Laurence P 2000 Phys.Rev.Lett.85 5543

[15]Giltner D M,McGowan RW,Lee SA 1995 Phys.Rev.A 52 3966

[16]Oberthler M K,Abfalterner R,Bernet S,Schmiedmayer J 1996 Phys.Rev.Lett.77 4980

[17]Kunze S,D¨urr S,Rempe G 1996 Europhys.Lett.34 343

[18]Kozuma M,Deng L,Hagley EW 1999 Phys.Rev.Lett.82 871

[19]John L,Mara P 1994 Phys.Rev.Lett.72 993

[20]Wallis H,1995 Phys.Rep.255 203

[21]Adams CS,Riis E 1997 Prog.Quant.Electr.21 1

[22]Dalibard J,Jannoadji CC 1989 J.Opt.Soc.Am.B 6 2023

[23]Unger PJ,Weiss D S,Riis E,Chu S 1989 J.Opt.Soc.Am.B 6 2059

[24]Chu S 1998 Rev.Mod.Phys.70 685

[25]Yu X C,Mo Y 2004 Acta Phys.Sin.53 4075(in Chinese)[余学才,莫影2004物理学报53 4075]

[26]Yu X C,Ye Y T,Wu Y F,Xie K,Cheng L 2005 Sciencein China G 48 521

[27]Ashkin A 1978 Phys.Rev.Lett.40 729