整数小波提升分解的刀具磨损检测方法*

管声启 师红宇

(①西安工程大学机电工程学院，陕西西安 710048;②西安工程大学计算机科学学院，陕西西安 710048)

数控机床刀具磨损量的检测通常采用人工检测刀具磨损情况，这种检测方法很容易受检验人员的经验、心理以及检测环境变化的影响，因此检验存在着一定不确定性，不利于制造集成化发展。

近年来，随着图像处理技术的发展，基于计算机视觉的刀具状态监测逐步进入机械自动化的领域，人们进行了广泛的研究，提出了许多的检测方法。文献［1］提出了基于改进型的脉冲耦合神经网络的刀具磨损检测方法，这种方法能把刀具磨损区域、刀体和背景分割出来，但要是想得到最佳分割效果，需要选取合适的网络参数和迭代次数。文献［2－5］分别采用不同的方法对工件的纹理进行分析，试图通过分析工件的纹理特征来判断刀具的磨损状态，但这类方法目前还没有形成一个公认的标准，还处在探索研究阶段。由于刀具种类的多样性，切削条件的多变性，这些方法普遍存在环境适应能力差、检测对象单一等问题，因此传统的方法很难适应自动实际检测的需要［6－8］。本文利用小波提升格式进行整数小波的单层分解，然后对单层分解的小波子图进行融合从而有效地消除冗余信息以及光照对检测的影响;在此基础上，进行OUST分割从而有效地实现刀具磨损量的检测。

1 整数小波提升分解

在小波变换过程中，传统小波变换的滤波器输出是浮点数，而图像的像素值均为整数，小波系数量化时存在舍入误差，由于存在计算误差，不能精确地重构图像。1995年，Sweldens利用提升格式对小波的构造提出了一种新的观点，即小波提升方案(Lifting Scheme)，也称之为第二代小波变换。小波提升格式具有真正意义上的可逆性。与传统小波变换相比，提升方案主要有如下优点:(1)继承了第一代小波的多分辨率的特性，图像的恢复质量对输入序列的长度没有任何限制，具有对任意尺寸图像进行变换能力;(2)小波的构造完全在空域内进行，无需傅里叶分析理论;(3)所用到的工具相当简单，主要为Laurent级数的Euclidean除法，所有的传统小波可以由提升方案中基本的提升和对偶分解而成;(4)运算速度快，节省存储空间;(5)可以实现整数到整数的变换。

1.1 整数小波提升分解过程

提升格式有分裂(Split)、预测(Prediction)和更新(Update)这3个过程。

(1)分裂

设初始信号为 si{si，k，k∈z}，将其分裂为两个互不相交的子集，偶数序列为 ei－1={ei－1，k，k∈z}和奇数序列{oi－1}。

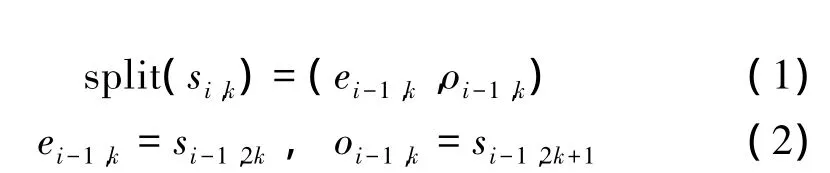
(2)预测

根据数据的相关性，用偶数序列去预测奇数序列，预测结果存在的误差称为小波系数di－1，k，即细节高频部分。然后用它来代替 oi－1，k。

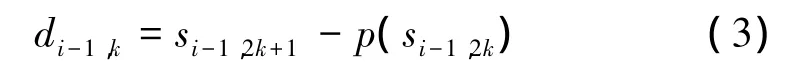
式中:p为预测算子。

(3)更新

对分裂和预测产生的结果的修正，使用更新算子u作用在小波系数di－1，k上，再与偶数序列相加便得到相应的尺度系数，这是对原始信号尺度的一种逼近。

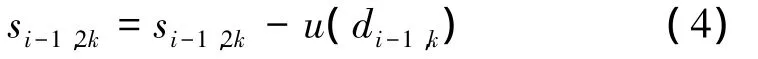
可以看出，提升方法容易实现快速算法，逆变换只需要按同样的步骤反方向进行，与正变换具有相同的复杂度，并且容许原位计算。另外，如果小波滤波器的系数是浮点数，那么其输出结果仍然是小数。输出结果的小数部分是由其中的“预测”和“更新”滤波器引入的，所以只要对其取整即可得到整数小波变换。这样，可以避免浮点运算。即式(3)和(4)可改写为

其中，［］表示取整操作。可以看出，整数小波是建立在提升算法的基础上，它的优点是小波变换后的系数是整数，运算速度快，节省计算机内存，有利于实现检测的硬件化。在同一硬件条件下，通过离散小波(DWT)三层变换和整数小波(IWT)三层提升变换处理速度结果如表1。可以看出，整数小波的变换能够有效地提高处理速度。

表1DWT与IWT变换时间比较

1.2 提升算子的确定

根据提升算法可知，提升过程需要确定预测算子p和更新算子u;根据双正交小波滤波器，从Laurent多项式的多相位分解确定小波提升算子，具体过程如下。

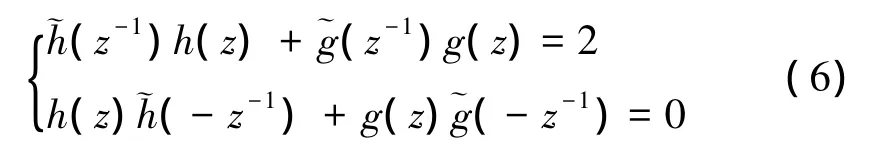
根据双正交小波重构条件及相关分析，对于多相位矩阵 p(z)，总存在 Laurent多项式ui和 pi(1≤i≤n)，使得p(z)有如下的分解:

2 整数小波分解子图的融合

根据小波的多分辨率理论可知，利用小波通过小波多层分解，刀具图像不同方向和不同频率的信息被分解在不同层次的各子图上，只要对这些细节子图特征进行研究，就可以获得需要的信息。然而，小波分解层数如何确定，目前还没有统一的方法来确定;另外，小波分解的层数越多，计算量也就越大，这将不利于快速在线检测。因此，本文提出了小波的单层分解用于刀具的磨损检测。整数小波单层分解的近似子图(LL)反映了刀具图像磨损的近似低频信息，水平(LH)、垂直(HL)及对角线(HH)子图分别反映了刀具磨损的水平、垂直及对角线细节高频信息，通过对这些子图的处理就能够检测出磨损的信息。

2.1 近似子图的零均值化

近似子图通常包含着刀具磨损的低频近似信息，同时也包含着光照强度不同而造成的干扰信息，这将严重影响刀具磨损信息的检测。为此，本文采用了零均值化的方法消除这种光照的影响。零均值化图像的构造过程:

设图像Fi，j大小为M×N，则将图像划分为8×8的窗口，然后每个窗口灰度均值为

其中:0≤i≤M－1，0≤j≤N－1。

然后进行采样，并进行双线性插值，延伸到原来的尺寸。这里的双线性插值公式为

最后，利用原采集图像与插值获得的图像相减，从而获得零均值图像，其公式为

2.2 子图融合过程

小波分解的水平细节(LH)和垂直细节(HL)子图主要保留了刀具磨损的高频细节信息;对角线子图(HH)主要体现了高频信息，最主要的是噪声信息。因此，选择小波提升分解近似(LL)、水平(LH)和垂直(HL)细节子图进行相加融合。

由于各子图的能量通常不在同一个量级，因此在子图融合前，先需要对各子图进行标准化处理，即对各子图像素数值按式(13)进行调整。

2.3 刀具磨损图像oust分割

融合后的标准图像缺陷的分割是采用最大类间方差自动阈值分割法，即oust自动分割法;其基本思想是用阈值把图像像素划分为两类，通过使划分后得到的两类的类间方差最大来确定最佳阈值。

设图像具有L级灰度，对每个灰度值f，Pf表示f出现的频率，此时分割阈值为t，则将灰度分成两类:

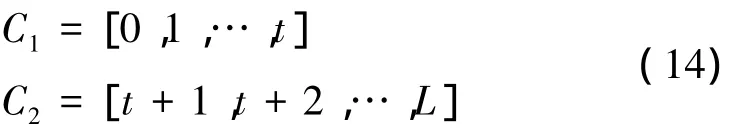
则出现的概率分别为

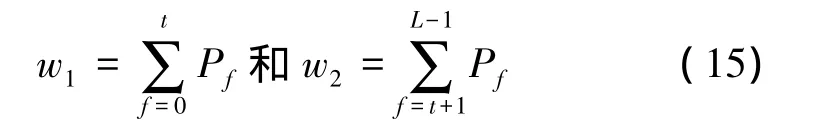
而每一类的平均灰度为

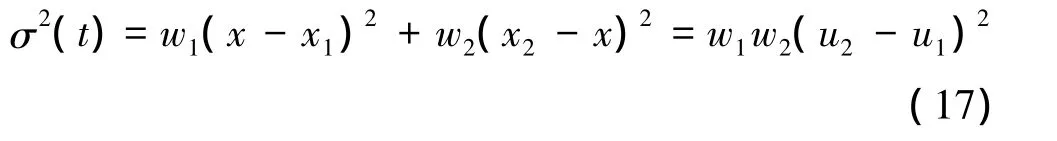
使σ2(t)取最大值时的t值就是最佳分割阀值。

3 刀具磨损检测过程及实验分析

3.1 刀具磨损检测过程

在刀具机械切削加工中，刀具出现的磨损主要有后刀面磨损、前刀面磨损、边界磨损等磨损情况;但多数情况都会发生后刀面磨损并且后刀面磨损带宽度测量方便，所以一般采用后刀面磨损来衡量磨损情况。本文实验是选用硬质合金刀具后刀面磨损图像作为测试图像如图1所示。

刀具磨损检测过程共分为3个步骤:

(1)刀具图像的整数小波提升分解;

(2)整数小波子图的融合;

(3)融合图像的分割。

选取具有良好的紧支性、高消失距和近似对称的DB4小波进行整数化单层提升分解，刀具磨损检测结果如图2所示。

从图2可以看出，采用本文的方法能够有效地检测刀具磨损的区域。

3.2 刀具磨损检测实验分析

为了验证本文算法的有效性，分别对刀具磨损图像采用最大熵自适应法、零均值化Oust法以及本文算法进行对比实验，其检测结果如图3所示。

其中，零均值化Oust分割法是指先将测试图像划分成若干子窗口，然后计算各子窗口灰度均值，并与测试图像相应子窗口像素灰度值相减，从而构成零均值图像;在此基础上，对零均值图像进行oust分割。

可以看出，最大熵自适应法无法完全实现刀具正常区域与磨损区域的分离，所以不能有效地检测出磨损区域;零均值化的Oust分割法虽然能够检测出磨损区域，但检测的磨损区域明显小于实际磨损面积;而本文所采用的方法不仅能够准确检测出磨损的区域，而且算法简单，因此很容易实现对刀具磨损缺陷的快速自动检测。

另外，当直接对测试图像进行Oust分割，发现无法实现目标从背景中分离出来，分析原因主要是光照不均匀影响所造成的，可见如何消除光照不均匀的影响会直接影响检测结果。

4 结语

通过对刀具后刀面磨损图像进行小波的整数提升分解，实现了不同刀具图像信息的分离;然后对分解的近似子图进行零均值化从而有效地抑制了光照不均对检测的影响;通过选择合适的子图融合达到消除噪声和减少计算量，最后通过Oust分割法实现了刀具磨损的快速检测。由于采用提升算法进行整数小波单层分解，使得算法简单、计算量减少，很容易实现硬件化，从而为在线自动检测提供了途径。

另外，本文在近似子图零均值化过程中，子窗口划分的大小对检测的结果会产生一定的影响，子窗口大小的确定将要做进一步的研究。

［1］李鹏阳，祝双武，郝重阳，等.基于改进型脉冲耦合神经网络的刀具磨损图像检测［J］.西北工业大学学报，2008，26(2):194－198.

［2］郑建明，李鹏阳，李言，等.基于Hough变换的刀具磨损监测加工表面纹理特征提取［J］.机械科学与技术，2009，28(6):17－21.

［3］熊四昌，计时鸣，樊炜，等.基于马尔科夫随机场加工表面纹理模型的刀具状态监测［J］.中国机械工程，2004，15(8):678－680.

［4］Kassim A A，Mannan M A，Zhu M.Texture analysis methods for tool condition monitoring［J］.Image and Vision Computing，2007，25(7):1080－1090.

［5］周承新，程慧琴.基于加工表面纹理连通区域的刀具磨损状态研究［J］.机床与液压，2010，38(5):42－45.

［6］张锐.基于计算机视觉的刀具磨损检测技术的研究［J］.机械工程与自动化，2008(4):107－109.

［7］林琳，高平，刘献礼，等.刀具前刀面磨损的图像检测［J］.哈尔滨理工大学学报，2000，5(5):43－46.

［8］Badley C，Wong Y S.Surface texture indicators of tool wear－ a machine vision approach［J］.The International Journal of Advanced manufacturing Technology，2001，17(6):435－443.