基于整体叶轮加工后置信息的五轴机床整体结构配置优化

梅方华 陈五一

(北京航空航天大学机械工程及自动化学院，北京 100191)

对于曲面曲率变化较大的复杂工件加工，五轴机床各轴运动速度发生剧烈变化，惯性力对机床影响较大，这对五轴机床在高加速度下的动力学特性提出了很高的要求。为获得良好的高加速五轴机床动态性能，人们做了大量研究，主要有以下方面:机床结构动态特性优化［1］、刀位轨迹光顺性及进给速度规划［2－3］、伺服控制系统加减速度优化［4］、伺服系统优化［5］。机床结构动态特性优化主要是提高机床静态刚度和动态固有频率，通过改变机床局部结构来实现;刀轨规划和进给速度规划主要是从待加工复杂工件表面特性的角度对加工工艺和加工参数进行优化;而伺服控制系统和伺服系统主要是从机床响应能力上进行优化。以上这些工作，都没有把机床结构动力学优化与加工工件直接联系起来。当我们需要大批量生产某种复杂工件时，可根据工件的加工特性，如工件尺寸规格、工件曲面曲率特点，分析工件加工时的动力学特性，研发专用机床，为机床加速度最大的运动轴配置最小的结构质量，实现整体惯性力最小，达到机床结构配置的整体优化。后置信息记录了数控加工运动的一切必要信息:工件加工的工艺顺序，各轴位移量，工艺参数(主轴转速，进给速度)［6］。通过这些参数可以计算各轴加速度，进而以机床惯性力最小为目标函数进行机床结构优化配置。本文以发动机整体叶轮这一典型复杂曲面工件为例，利用数控编程软件对待加工自由曲面进行编程，根据五轴机床结构和数控系统控制器生成后置信息，基于后置信息，对五轴机床进行结构优化配置。

1 整体叶轮HyperMill精加工编程

本文利用HyperMill对轴流式整体叶轮进行数控编程，整体叶轮模型由文献［7］提供。由于只需进行叶片、流道及叶根圆角部分精加工，因此将叶轮其他部分进行简化，只保留叶轮部分结构如图1所示。叶轮直径205 mm，最小内径150 mm，叶轮高度19 mm，叶片最大厚度0.78 mm，叶轮叶片数37。

HyperMill五轴叶轮循环加工模块包括5X叶轮粗加工、5X叶轮流道精加工、5X叶轮点加工、5X叶轮侧刃加工、5X叶轮边缘加工、5X叶轮圆角加工。

(1)叶轮叶片点加工

5X叶轮侧刃加工适用于直纹面叶片精加工，叶片扭曲率较大时，叶片部分精加工只能用5X叶轮点加工。由于工件最终尺寸叶片间距最小处为8.609 mm，因此可能选择的刀具为φ5 mm、φ6 mm的通用球头铣刀，尝试先用φ6 mm的球头铣刀加工，出现刀轨不光滑现象，因此选用φ5 mm的球头铣刀。叶片点加工路径如图2所示。

(2)叶轮流道加工

叶轮流道加工选用与叶轮叶片点加工部分相同的刀具，叶片流道精加工路径如图3所示。

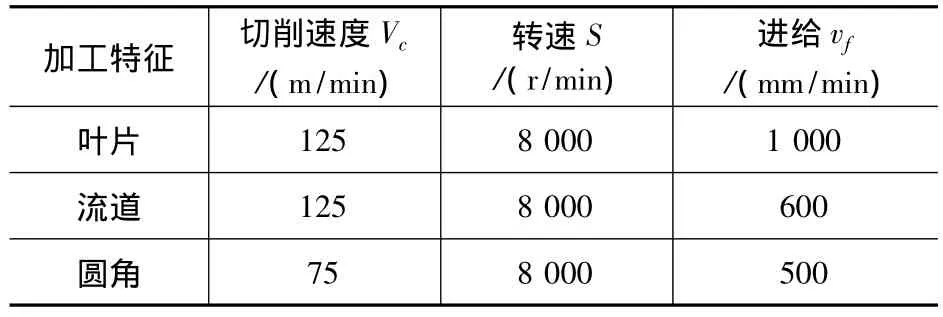
表1 整体叶轮加工工艺参数

(3)叶轮圆角加工

对于R1.5 mm叶根圆角采用φ3 mm的球头铣刀进行精加工余量去除，圆角精加工路径如图4所示。整体叶轮精加工各部分加工参数如表1。

本文所选择的优化机床为AC轴双摇篮，根据机床信息生成后置处理器，导入HyperMill生成叶轮精加工后置信息。

2 整体叶轮加工后置信息提取

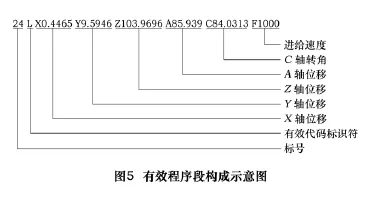
后置信息文件中的G代码除了包含机床五坐标轴的位移信息和进给速度信息，还包括工件模型、刀具、机床零点、加工精度、转速等信息。在本文中，我们称包含机床轴位移信息或进给速度信息的程序段为有效程序段。有效程序段构成如图5所示。

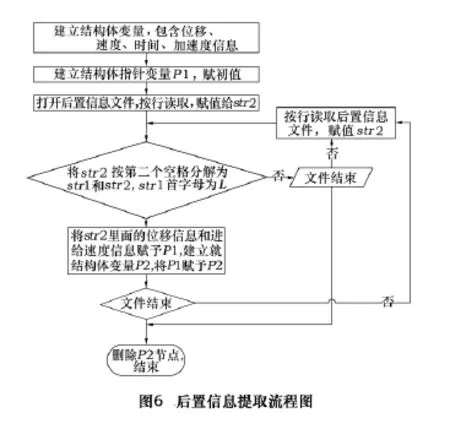
建立后置信息结构体变量，该结构体变量包含五轴机床各轴位移量、进给速度等变量成员。在按行读取后置信息后，将读取的信息按空格分隔符进行分解，根据分解的第2个字符串判断程序段的有效性。对于有效程序段，继续按空格为分隔符对程序段进行分解，根据分解后所得信息中的字母，判断字母后面的数值信息类别，然后将所得信息存入相应的结构体变量成员中。后置信息提取过程如图6所示。

3 整体叶轮各特征加工机床各轴加速度信息计算

多坐标插补器通常按照六坐标设计:X、Y、Z、A、B、C，实际使用中根据机床结构选用A、B、C转角中的任意两个［8］。

插补线段长度:

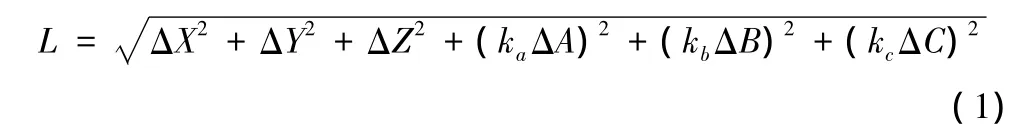
它是直线和转角的合成长度，在计算时将角度单位直接变化为mm单位，式中看ka、kb、kc为速度匹配系数，由系统参数设定。AC轴双摇篮机床为正交机床，可取 ka=1，kb=0，kc=1。

由五轴机床插补器原理可知:

根据位移值以及进给速度，得到各轴位移量所对应的时间，将以上得到位移、时间写入文件。对于各刀位点的速度、加速度处理方法如下。

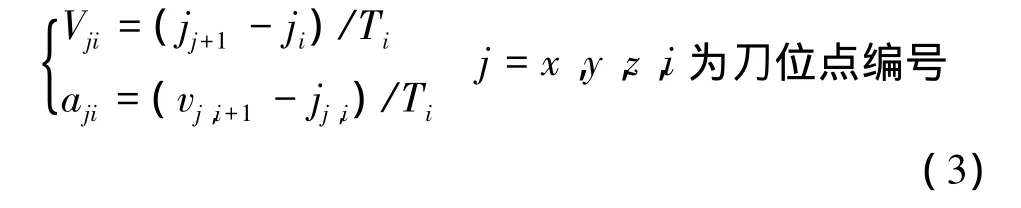
各轴最大加速度计算公式:

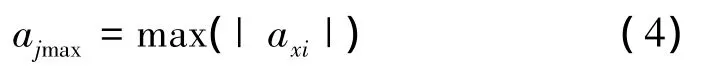
各特征各轴最大加速度绝对值如表2所示。

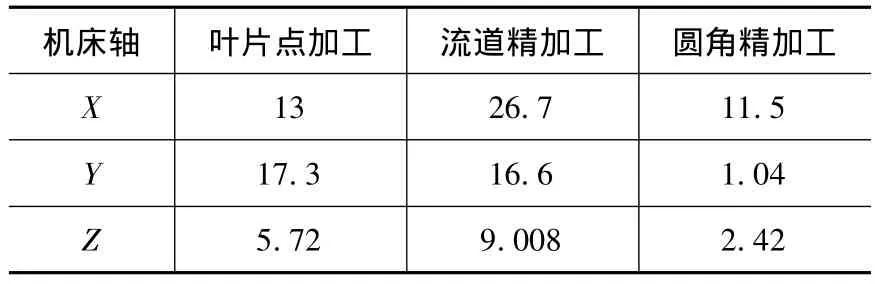
表2 各特征加速度最大值 ×10－2g

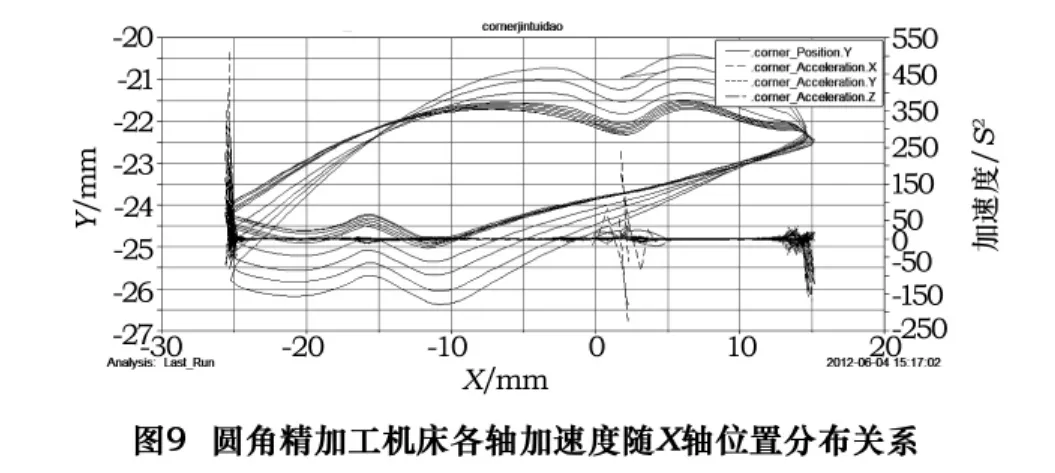
同时，本文将以上得到的位移文件和时间文件通过CUBSPL函数导入ADAMS进行运动学仿真。此时，横坐标应该为位移变量而不是时间变量，计算结果如图7～9所示。图7中横坐标为Y轴位移，纵坐标为Z轴位移及X、Y、Z轴加速度;图8中横坐标为Y轴位移，纵坐标为X轴位移及X、Y、Z轴加速度;图9中横坐标为X轴位移，纵坐标为Y轴位移及X、Y、Z轴加速度。

从图7～9可知，在各特征加工过程中，机床X、Y、Z轴边缘部分加速度较大，处于该状态时间较短，在其余部分加速度较小，机床处于该状态时间较长。本文对处于高加速度状态与低加速度状态的刀位点予以统计。

加速度点统计公式如下:

式中:nj为j轴加速度绝对值大于aj的刀位点个数;F(aj)为j轴加速度绝对值大于aj的刀位点的比例;N为刀位点总数。

本文将大于加速度最大值0.8倍的区域定义为相对高加速度区域，将加速度小于最大加速度0.2倍的区域定义为低加速度区域。统计结果如表3所示。

表3 各特征加速度分布

由表3可知，在整体叶轮各特征部分，处于高加速度区域的刀位点数量最高不到0.1%，而处于低加速度区域的刀位点数量超过96%。整个加工过程中机床各轴大部分时间处于低加速度运行状态。各轴最大加速度代表了机床运行过程中出现的极端情况，但是机床处于最大加速度的运行状态时间较短。因此，当我们从机床整体运行状态的角度对机床结构进行优化配置时，需要将机床运行过程中的加速度分布考虑进去。高加速度值对机床运行状态影响较大，而低加速度值对机床运行状态影响较小，同时各加速度值所占比例的大小也影响到机床运行状态。因此本文以各刀位点的加速度值以及刀位点总数的倒数作为各刀位点加速度在整个加工过程中的权重因子，计算加权加速度。

加权值计算公式如下:

经计算，各特征加工加速度最大值、加速度加权值如表4。计算各轴整体加速度权值时，刀位点总数为整体叶轮加工所有刀位点。

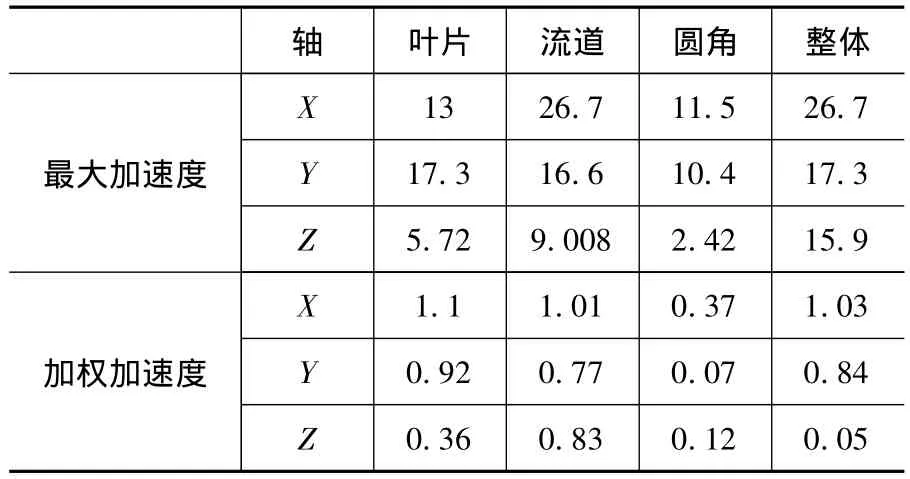
表4 整体叶轮加工后置信息综合分析×10－2g

4 基于后置信息分析结果的五轴数控机床整体结构配置优化

机床结构配置和运动组合的基本原则是［9］:轻量化原则、重心驱动原则、对称原则、短悬伸原则、短路径原则、封闭原则。关于轻量化设计原则，现代设计理念认为:机床结构件设计的成功关键在于结构件的形状和筋板的合理布置，在轻量化的同时，实现高比刚度［10］。在此，本文提出了一种新的机床结构配置方法，从运动链重构的角度来减小机床运动过程中的最大惯性力，实现轻量化，提高机床动力学性能。

叶轮加工一般采用双摇篮五轴机床，其3个线性轴模型简图如图10所示。

根据机床构型，Y轴在运动链中离工件最远，Y轴移动时带着机床X、Z轴一起运动，因此有:My=mx+my+mz。

同理有:Mx=mx+mz，Mz=mz。

其中，Mx、My、Mx为不考虑转动轴影响情况下 X、Y、Z轴等效移动质量。

各线性移动轴实际质量参数为:mx=305 kg，my=600 kg，mz=265 kg。

根据各轴等效移动质量和最大加速度计算各轴最大惯性力。

最大惯性力计算公式如下:

其中:Fjmax为j轴最大惯性力;Mj为j轴等效移动质量;ajmax为j轴移动最大加速度。

根据各轴等效移动质量和加权加速度计算各轴加权惯性力。

加权惯性力计算公式如下:

各轴惯性力计算结果如表5。其中:

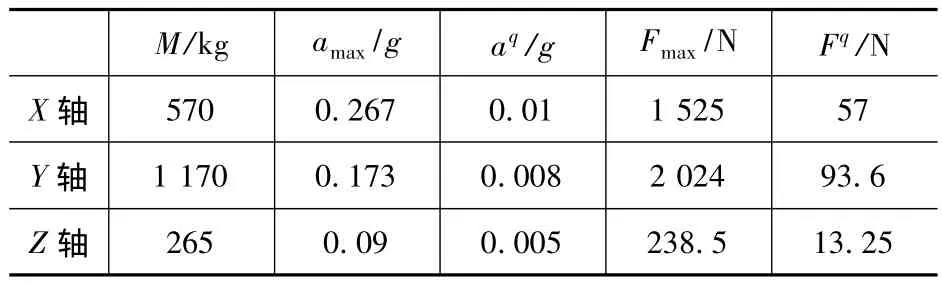
表5 优化前最大惯性力与加权惯性力

M为等效移动质量;amax为最大加速度;aq为加权加速度;Fmax为最大惯性力;Fq为加权惯性力。

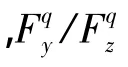
表6 优化后最大惯性力与加权惯性力

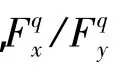
优化前，机床整体结构最大惯性力:

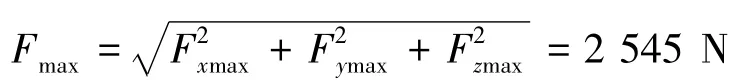
优化后，机床整体结构最大惯性力:

经过运动链重构，机床整体结构最大惯性力减小42.3%，机床整体结构加权惯性力减小44.5%，机床最大惯性力差异比减小59.7%，机床加权惯性力差异比减小39.1%。

5 结语

提出了一种基于整体叶轮后置信息的专用五轴机床结构配置优化方法，该方法能够从整体叶轮加工过程中机床极端运行动力学状态和机床整体运行动力学状态对机床结构进行动力学优化，提高专用机床的动力学特性。经过运动链重构，机床整体结构最大惯性力减小34%，机床整体结构加权惯性力减小44.5%，机床最大惯性力差异比减小59.7%，机床加权惯性力差异比减小39.1%。

［1］Liu Shihao，Ye Wenhua，Lou Peihuang，et al.Structural dynamic optimization for carriage of gantry machining center using orthogonal experimental design and response surface method［J］.Journal of The Chinese Society of Mechanical Engineers，2012，33(3):211－219.

［2］Xu Rufeng，Chen Zhitong，Chen Wuyi.Tool positioning algorithm based on smooth tool paths for 5－axis machining of sculptured surfaces［J］，Chinese Journal of Mechanical Engineering，2011，24(5):851－858.

［3］Beudaert Xavier，Lavernhe Sylvain，Tournier Christophe.Feedrate interpolation with axis jerk constraints on 5－axis NURBS and G1 tool path［J］.International Journal of Machine Tools ＆ Manufacture，2012，57(10):73－82.

［4］赵国勇.数控系统运动平滑处理、伺服控制及轮廓控制技术研究［D］.大连:大连理工大学，2006.

［5］苏志远.面向高速高加速度运动伺服系统的自寻优模糊控制研究［D］.合肥:合肥工业大学，2007.

［6］张朋辉.CAD/CAM系统反读取G代码功能的实现［D］.大连:大连理工大学，2006.

［7］李湉.航空发动机整体叶轮加工与修复关键技术研究［D］.北京:北京航空航天大学，2010.

［8］郇极，靳阳，肖文磊.基于工业控制编程语言的IEC 61131－3的数控系统软件设计［M］.北京:北京航空航天大学出版社，2011:98－104.

［9］张曙，卫汉华，张炳生.机床结构配置的新思路［J］.制造技术与机床，2011(10):8－11.

［10］杨永彬，陈五一，赵大海.机床立柱高比刚度结构仿生设计［J］.北京航空航天大学学报，2008，34(9):991－994.