基于边缘值、方差以及脉冲性的偏微分方程图像去噪算法

侯传勇

（中北大学信息与通信工程学院，太原 030051）

1 引言

自20世纪80年代以来，计算机技术得到迅猛发展，性价比越来越高，从而为数字图像处理和计算机视觉的迅速发展奠定的物质基础，其应用也日趋扩展。图像去噪[1]是数字图像处理中的一个经典问题。偏微分方程（PDE）因为具有各向异性的特性，并且自适应性强，所以将其应用在图像去噪过程中时能够在平滑噪声的同时更好的保持边缘纹理等细节信息。在过去的二十几年中，偏微分方程算法获得了巨大的发展。

从理论上看，利用偏微分方程进行图像去噪可以追溯到很早以前。1990年，学者Perona和Malik[2]在热传导方程的基础上提出了著名的图像去噪模型：P-M模型。但是，由于P-M方程在解的存在唯一性上缺乏相应的理论基础，因此，F.Catt[3]等学者于1992年对P-M模型进行了改进，在数学理论上解决了解的存在唯一性，完善了这个模型。1994年，J.Weickert[4]利用扩散张量为扩散项，提出了基于张量的偏微分方程模型，克服了非线性扩散方程无法去除图像边缘处噪声的缺点。随后，Osher[5]和他的研究小组提出了基于全变分的图像消噪模型。此外，偏微分方程去噪模型还实现了由低阶向高阶[6]等的发展。

现有的偏微分方程去噪模型因为在扩散的时候没有考虑图像本身的具体特征，所以去噪的同时不能特别清晰的保护图像的具体细节信息。本文在原有偏微分方程模型的基础上，结合图像的边缘值、方差以及脉冲性等特征，提出了一种改进的基于偏微分方程的图像降噪算法。该算法利用边缘值、方差跟脉冲性来确定扩散的程度，进而确定各项异性扩散的强度，从而起到很好的降低图像噪声的作用。

2 P-M模型原理

1990年，Perona和Malik提出了各向异性扩散模型（P-M模型），该模型用一个能保持边缘的具有自适应的各向异性扩散替代高斯平滑。P-M模型根据具体区域来调节模型的扩散系数，使扩散主要发生在图像的平滑区域，而在边缘处则停止扩散。因此随着扩散过程的进行，平滑区域的噪声越来越少而非平滑区域的噪声则得到较好的保持。

Perona和Malik提出了能够保持边界的各向异性扩散方程：

其中，It(x,y)是t时刻的图像; div是散度算子；∇ It(x,y)是梯度算子；ct是依赖于图像的扩散系数。通过适当的定义扩散函数，Perona-Malik模型既可以去噪，又可以很好的保护图像的边缘细节信息。

设想 It(x,y)是图像在第t次迭代后坐标(x,y)处的灰度值；I0(x,y)是原始输入图像。各向异性扩散模型可以通过使用四个邻域和拉普拉斯算子离散得到：

t也可以被认为是Perona-Malik各向异性扩散模型梯度(x ,y)的映射。即：

在Perona-Malik各向异性扩散模型中，扩散系数可由以下公式给出：

其中，参数k是一个常数，在扩散系数函数中是一个边缘强度阈值,通常是一个正整数。

但是单纯的用梯度信息来控制扩散强度并不能清晰的反映图像的细节信息。因此本文在原有P-M模型的基础上引入了图像的边缘值、方差以及脉冲性等特征。

3 算法改进

边缘值体现了灰度图像中突出变化的部分，我们使用sobel算子[7]来计算像素的边缘值[8]。边缘值的计算公式如下：

其中，1s为行边缘算子，2s为列边缘算子。

图像的标准偏差[9]描述了图像在3×3邻域中的分布，可以用以下公式求得：

其中 iju为为3×3邻域中灰度均值，d=3表示3×3邻域。

图像的脉冲性[10]：

结合图像的特征和扩散过程中的梯度,扩散系数函数(公式5)可以写为

将以上三种图像的描述方法结合到一起即：

其中，k0为一个边缘强度阈值，通常是一个正整数。

在修改后的扩散系数函数中，边缘强度阈值k0与梯度和边缘值、标准偏差以及脉冲性结合，即可得到修改后的扩散模型。在梯度变化大的地方，图像的灰度值变化大，HO值大，为边缘区，需要保留；在梯度变化小的地方，图像的灰度值变化平缓，HO值小，为非边缘区域，可以进行扩散平滑处理。

图1 Lena图像原图

图2 加噪声结果

图3 边缘值降噪结果

图4 标准偏差降噪结果

图5 脉冲降噪结果

图6 HO模型降噪结果

为了检测本算法对图像噪声的抑制效果，本文以Lena图像作为原始图像。图像加入以u取0，σ2取0.001的噪声数据模型。然后，对噪声图像分别采用偏微分模型和本文算法进行降噪处理。

如图1- 6所示，分别为原始图像、加噪声图像、基于边缘值的偏微分模型、基于标准偏差的偏微分模型、基于脉冲性的偏微分模型和基于HO的偏微分模型下的降噪结果。可以看出，每种方法都对噪声有一定的抑制效果。其中边缘值跟标准偏差方法可以很好的去除噪声，但是容易造成过平滑，不能很好的保护图像的细节信息；脉冲降噪方法在出去噪声的同时，容易造成伪影；基于HO的偏微分模型的降噪效果是最佳的，这种算法不仅能够很好的去除噪声，并且可以保护图像的边缘细节信息。

除了主观观察方法外，为了对该算法的效果进行客观、定性的评价，本文对重建的结果进行了定量的分析，采用均方误差和信噪比两种评价参数进行评价，定义如下：

均方误差MSE

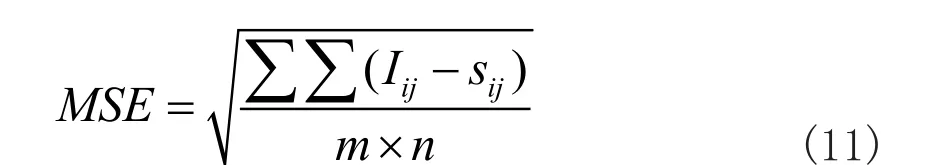
其中，ijI表示原始图像的第i行，第j列的像素灰度值；ijs表示去噪后图像的第i行，第j列的像素灰度值；MSE评价的是去噪图像跟真实图像的接近程度。MSE越小代表去噪图像跟原始图像越接近，去噪效果越好。

2)信噪比SNR

4 实验结果与分析

信噪比是用于比较重建图像与原图像质量的参数，信噪比数值越大，说明图像中的噪声越少。

表1 各种算法的重建图像质量评价参数

5 讨论与结论

本文采用一种改进的基于偏微分方程理论，针对图像的噪声问题，利用图像的3×3邻域中的边缘值、标准偏差和脉冲性等可以用来描述图像一个区域内的分布变化的特点，在偏微分模型中引入图像的边缘之、标准偏差以及脉冲性，并用改进的偏微分模型进行降噪。实验表明，改进的偏微分模型降噪后的重建图像效果较好，其中HO模型去噪效果最好，而且可以在有效的抑制图像的噪声的同时，保留图像的细节与边缘。但是在降噪过程中，计算程序复杂，程序运行时间较长，如何有效的改进，是进行下一步研究的内容。

[1] Dai Fang,Zheng Nanning,Xue jianru.Image smoothing and sharpening based on nonlinear diffusion equation[J].Signal Processing,2008,88(11)：2850-2855.

[2] Shahnaz Taheri,Qi Tang,Kewei Zhang.Young measure solutions and instability of the one-dimensional Perona–Malik equation[J].Journal of Mathematical Analysis and Applications,2005,308(2)：467-490.

[3] Lianhua He，Anping Liu. Existence and uniqueness of solutions for nonlinear impulsive partial differential equations with delay[J].Nonlinear Analysis： Real World Applications,2010,11(2)：952-958.

[4] Martin Welk，Gabriele Steidl，Joachim Weickert.Locally analytic schemes： A link between diffusion filtering and wavelet shrinkage[J]. Applied and Computational Harmonic Analysis,2008,24(2)：195-224.

[5] Ronald P. Fedkiw，Guillermo Sapiro，Chi-Wang Shu.Shock capturing，level sets，and PDE based methods in computer vision and image processing： a review of Osher’s contributions[J]. Journal of Computational Physics,2003,185(2)：309-341.

[6] John B. Greer，Andrea L. Bertozzi，Guillermo Sapiro.Fourth order partial differential equations on general geometries[J].Journal of Computational Physics,2006,216(1)：216-246.

[7] J Kittler.On the accuracy of the Sobel edge detector[J].Image and Vision Computing,1983,1(1)：37-42.

[8] Lorenzo Giacomelli.Non-linear higherorder boundary value problems describing thin viscous flows near edges[J].Journal of Mathematical Analysis and Applications,2008,345(2)：632-649.

[9] Xianwei Wu，David Jeff Jackson，Hui-Chuan Chen.A fast fractal image encoding method based on intelligent search of standard deviation[J].Computers & Electrical Engineering,2005,31(6)：402-421.

[10] Erkan Beşdok..A new method for impulsive noise suppression from highly distorted images by using Anfis[J]. Engineering Applications of Artificial Intelligence,2004,17(5)：519-527.