基于包围盒和三角面片的碰撞检测优化算法*

陈 晨 张为民 褚 宁

(①同济大学中德学院，上海 200092;②同济大学机械与能源工程学院，上海 201804)

五轴数控机床相比普通三轴机床多出两个旋转自由度，因此更容易发生各部件之间的碰撞干涉，其碰撞干涉检测一直都是五轴数控加工中的关键难题之一［1］。在各种碰撞算法中，层次包围盒法近年来得到了广泛的应用，它的设计思想是用体积稍大而特征比较简单的包围盒来描述待测的几何实体，并将包围盒与某种树型结构结合起来，从而形成层次结构来逐步逼近几何实体，根据包围盒层次结构建立层次包围体树，再遍历两个模型的包围体树来逐渐缩小模型的检测区域，以此减少整体的检测次数［2］。由于包围盒与几何实体之间通常存在一定的间隙，所以当检测到叶节点的包围盒相交时，需进一步进行基于三角形面片相交测试的精检测算法。传统的OBB包围盒和三角形相交算法存在精度和实时性上的不足，本文针对五轴机床的运动特性，对算法进行了改进。

1 基于层次包围盒的碰撞干涉粗检测

常用的包围盒包括:包围球(Sphere)，沿坐标轴的包围盒AABB(Axis－Aligned Bounding Boxes)，固定方向包围盒 FDH(Fixed Directions Hulls)，方向包围盒OBB(Oriented Bounding Box)［3］。其中 OBB 包围盒曾一度作为评价碰撞检测算法的标准，它的计算相对复杂，但紧密性是最好的。在大多数情况下，OBB包围盒的总体性能比AABB和包围球要好很多［4］。

1.1 OBB包围盒树存储方式的优化

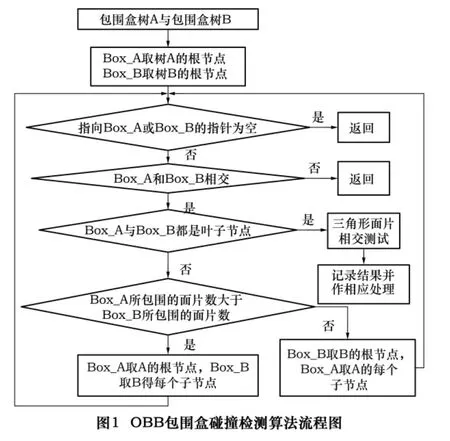
当两个几何实体的OBB层次包围盒树建立后，通过遍历两棵包围盒树对两个包围盒进行相交测试:当两个包围盒不相交时，以该包围盒为根节点的子树停止检测;当两个包围盒相交时，则对该节点的叶子节点进行相交检测;当检测到叶子结点的包围盒相交时，则执行基于三角形面片相交测试的精检测，其流程图如图1所示。

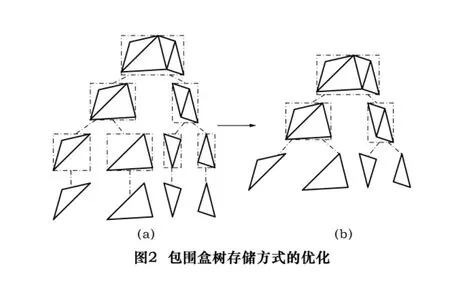
采用二叉树来构造包围盒树时，用递归的方法划分包围盒，根据子节点相对于分裂轴的空间位置将父节点划分为两个子集，直至每个叶结点只包含一个三角形面片为止。每个节点里存储了所对应的包围盒信息，而叶子节点里还包括三角形的几何信息，如图2a所示。对于含有N个叶子节点的包围盒树来说，其需要存储的节点数目为2N－1个，如果将原叶子节点的三角形信息放在其父节点里，跳过叶子节点包围盒间的相交测试，直接进行基本几何元素间的相交测试，这样只需要存储N－1个节点，基本去掉了一半的节点，从而节省了存储空间。在进行检测的时候，需要遍历的节点数目也明显减少，优化后的包围盒存储结构如图2b所示。

1.2 传统OBB包围盒构造算法分析

本文中待测对象的存储方式是基于三角形网格模型的STL格式，三角形的顶点集合可以看作是三变量的概率分布函数，则OBB包围盒的中心位置和方向可以利用三角形顶点的均值和协方差矩阵来计算。若第i个三角形顶点矢量为 pi，qi和 ri，三角面片的总数为n，则包围盒中心位置为:

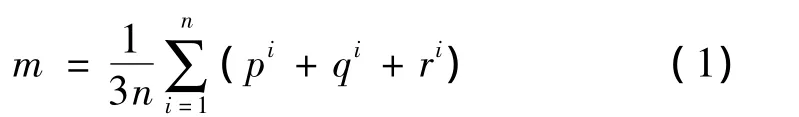
其协方差矩阵元素为:

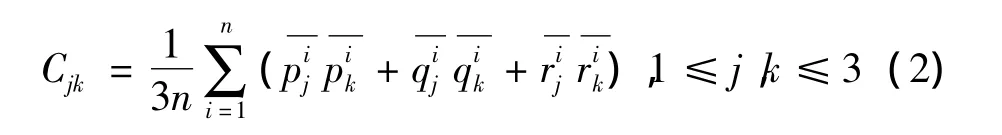
求解Cjk的特征向量并单位化。因为Cjk是一个实对称矩阵，所以其特征向量相互垂直，令它们作为包围盒的方向轴。将所有顶点投影到这3条方向轴上，计算出在轴上的最大和最小值，以此来确定包围盒的大小。

包围盒的中心位置是各个三角形顶点的简单平均，所以当构成几何实体的三角形的尺寸不均匀时，包围盒就会偏向三角形尺寸较小、分布较密的部分。这样就会导致包围盒和几何实体发生错位，显然这样会使包围盒的紧密性变差，并且使构造的包围盒树不平衡，从而影响到碰撞检测的效率和准确性。

1.3 OBB包围盒构造算法优化

选择三角形的面积作为权值，给每个三角形进行加权。设第i个三角形的面积为Si，则:

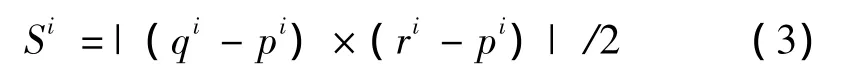
三角形面片表示的几何实体表面积为S，则:

第i个三角形的中心为Mi，则:

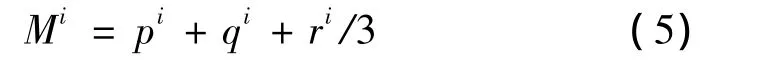
包围盒所包围的三角形带权中心为M，则:

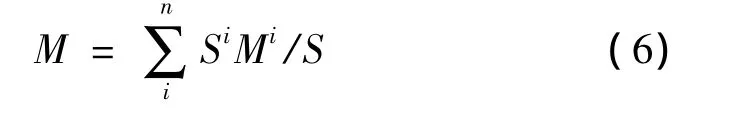
协方差矩阵C的元素为:

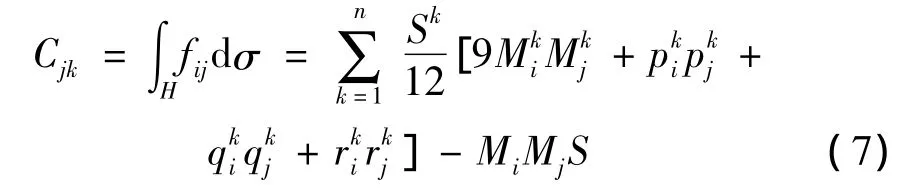
以此得到更精确紧密的OBB包围盒，包围盒间的相交测试可以看成某一个盒体是否完全位于另一个盒体某一面之外，凸块OBB包围盒的相交检测采用了Gottschalk［5］等基于分离轴定理提出的检测方法。如果包围盒间存在一条分离轴，那么可以判定它们是不相交的。

2 基于三角形面片的碰撞干涉精检测

2.1 三角形图元之间相交测试

提高碰撞检测的实时性一般从两方面入手:一是减少整体的检测次数，例如采用上文的层次树;二是减少图元之间相交检测的时间，因此研究快速的三角形相交检测算法有着十分重要的意义。

三角形快速相交检测算法主要可以分为标量判别型算法和矢量判别型算法。标量判别型算法是通过准确计算来获知两个三角形相交关系的一类算法，典型的有Möller、Held和Tropp算法;矢量判别型算法是通过三角形各顶点构成的行列式的正负几何意义来判断三角形中点、线、面间的相对位置关系，进而判断两个三角形是否相交，典型的有Devillers＆Guigue算法和Shen算法［6］。本文在前面几种算法的分析基础上，提出了一种优化算法，该算法可以在判断三角形是否相交的同时，得到相交的具体位置及深度信息，避免了复杂的三角形所在平面的计算，从而加快了计算速度，保证了系统的实时性。

2.2 空间三角形快速检测算法优化

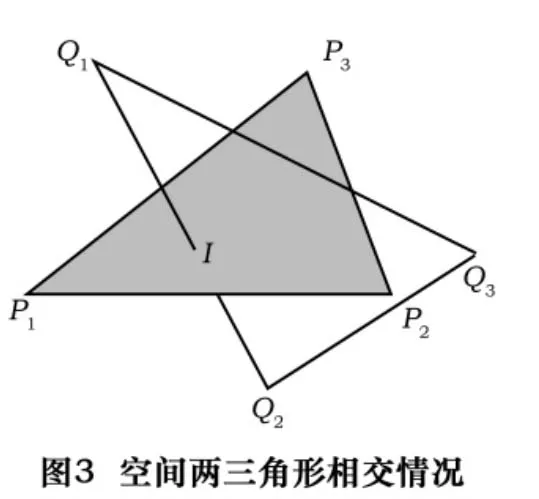
如图3所示:边Q1Q2所在的直线方程可以表示为L(t)=Q1+tD，其中 D=Q1－Q2。

设I(u，v)为ΔP1P2P3内任意一点，则其可以表示为:

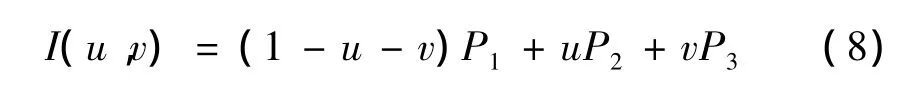
其中:u≥0，v≥0 且 u+v≤1。

求直线L(t)和ΔP1P2P3所在平面的交点可以等价于求解 L(t)=I(u，v)，即:

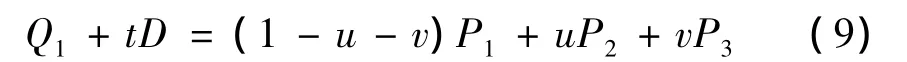
其中:t即为点Q1到三角形平面的距离。整理方程得:

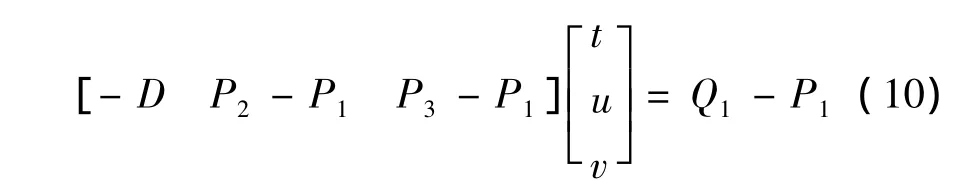
令 D0=Q1－P1，D1=P2－P1，D2=P3－P1，则方程可以转换为:

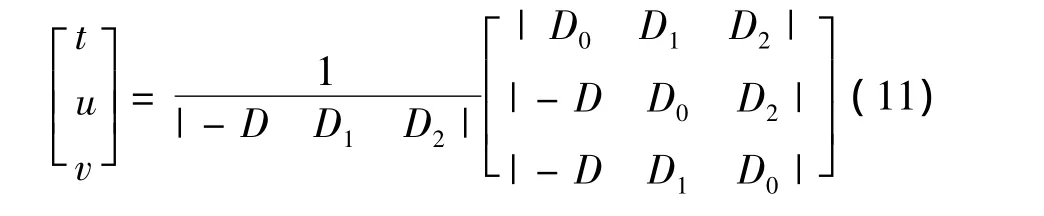
又由|X Y Z|=－(X×Z)·Y=－(Z×Y)·X可将方程进一步转换为:

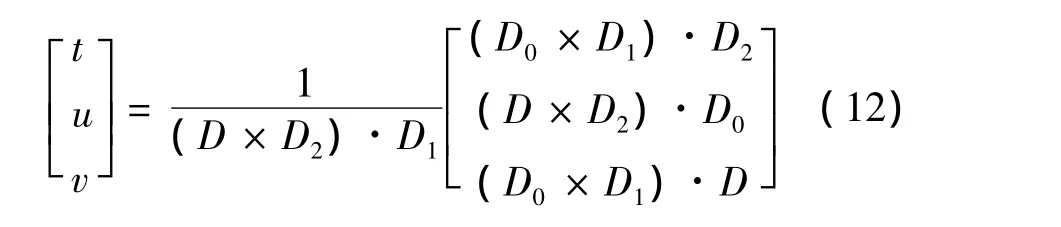
为了提高算法效率，首先计算u的值，若0≤u≤1，再计算v，以此求出交点I的坐标，比较Q1、Q2及I任意一轴向方向上的值，便可判断 Q1、Q2两点是否在ΔP1P2P3的两侧;若 u＜0或 u＞0，则不再计算 v，转而计算ΔQ1Q2Q3的其他两条边是否穿过ΔP1P2P3。当确定两个三角形已经相交时，计算t的值，即为Q1点离ΔP1P2P3所在平面的值。

2.3 三角形相交检测算法计算量比较

检测算法的时间消耗主要取决于开辟内存和数学运算两部分，开辟内存又取决于算法中所使用的变量数，而数学运算包括四则运算、比较运算、绝对值运算和赋值运算。目前主流的PC与数控系统中，加、减、乘和比较的计算时间可以认为是相同的，赋值运算的计算时间相对而言可以忽略，除法的计算时间大约是加法的4～8倍［7］。表1是检测如图3所示两个三角形相交时各种算法所使用的变量数以及计算量的比较［8］:

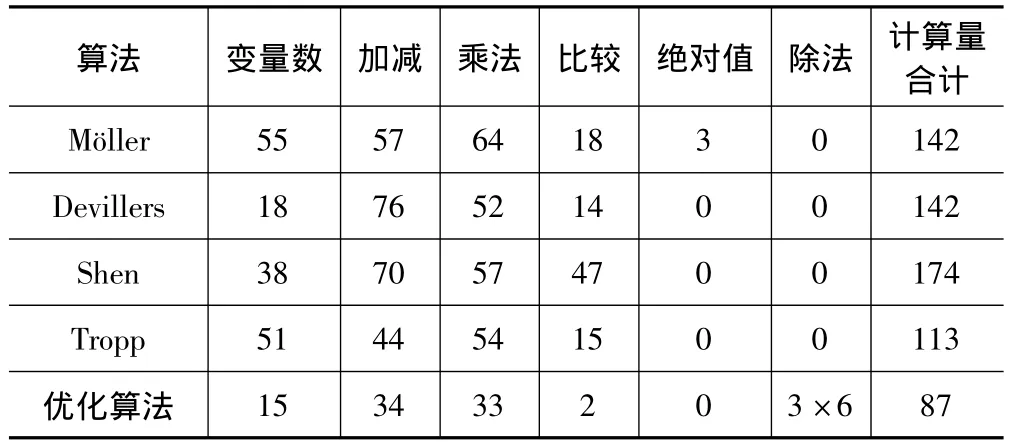
表1 各种三角形相交检测算法使用变量数及计算量比较

经过比较可以发现，优化算法所需的变量数较少，而且尽管提出的优化算法里有3个除法运算，但是加减法和乘法运算较其他几种算法明显减少，所以总的计算量得以大幅度减小，从而提高了算法的效率。而且待检测物体和参与运算的图元数量越多，优化算法的优越性就越明显。

3 仿真实验

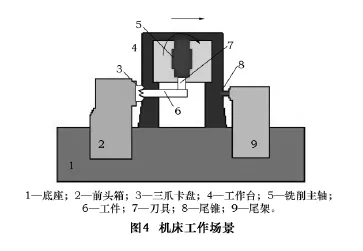
首先用Solidworks作图软件建立某车铣复合加工中数控机床的简化模型，使用OpenGL图形库对机床工作场景进行描述，并导出为基于三角形网格模型的STL格式。机床各部件所包含面片个数如表2所示。

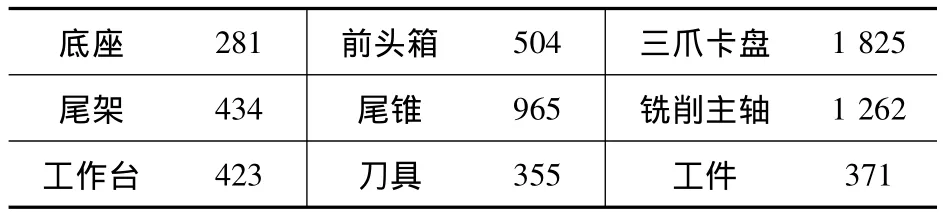
表2 机床各部件所含三角形面片数

模拟两种情况下的进给运动:(1)令刀具沿Z轴方向靠近工件和三爪卡盘，进给速度为100 mm/min;(2)令刀具作A旋转轴上的运动，进给速度为270°/min，如图4所示。仿真运行环境为:Pentium(R)Dual－ Core CPU E5400 2.70 GHz，内存2.0 GB，Windows 7系统，测试用VC++语言实现。

令刀具在两种运动形式中依次与工件和三爪卡盘发生碰撞干涉，分别使用包围盒树未经优化情况下的Tropp算法，Shen算法和三角形优化算法，以及包围盒树和三角形都经优化过的算法进行碰撞检测，并采集检测算法所需时间，耗时结果如表3所示。

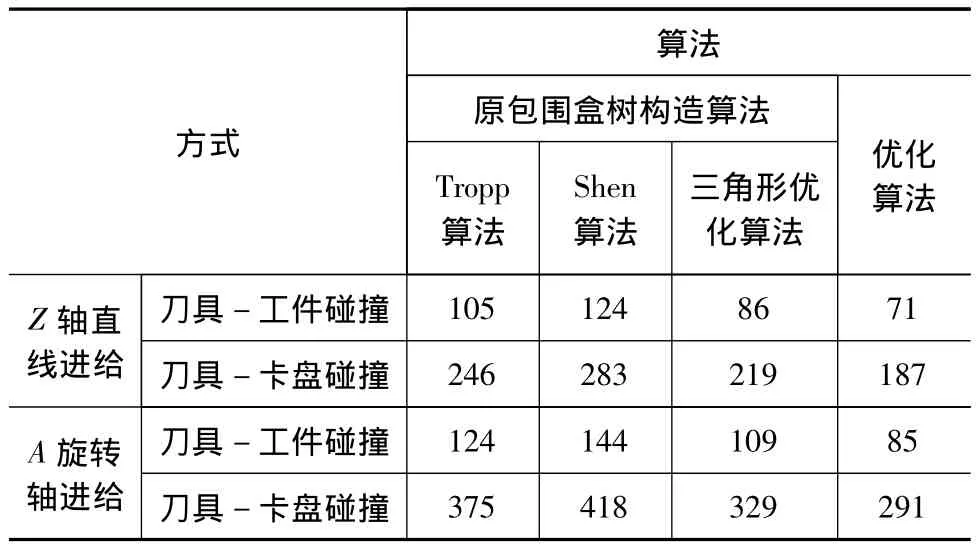
表3 算法优化前后耗时结果对比 ms

结果表明优化算法有效地加快了碰撞检测的速度，而且待检测三角形数目越多，效果越明显。

4 结语

本文将基于OBB包围盒的碰撞干涉检测优化为粗检测和精检测两部分，粗检测采用改进的OBB层次包围盒算法，精检测采用基于三角形面片相交检测的优化算法，在保证运算精度的情况下提高了检测速度。在粗检测部分通过省去二叉树结构中叶子节点，直接进行基本图元间的相交测试，从而改善了包围盒树的存储结构，采用改进的OBB包围盒构造算法保证了包围盒的紧密性和准确性。在精检测部分提出了一种基于三角形面片相交检测的优化算法。该算法不仅能够快速有效地判断出两个三角形面片之间是否存在相交情况，而且能够快速地计算出交点的具体位置以及相交的深度值，从而提高了碰撞检测的精度。通过仿真实验，验证了该优化算法的有效性。

［1］Ding S，Mannan Ma，Poo An.Oriented bounding box and octree based global interference detection in 5－axis machining of free－form surfaces［J］.Computer－ Aided Design，2004，36:1281 －1294.

［2］朱晓耀.数控系统在线防碰撞系统的碰撞检测算法的设计与实现［D］.上海:同济大学，2011:20 －21.

［3］石教英.虚拟现实基础及使用算法［M］.北京:科学出版社，2002.

［4］赵呈浩.数控机床仿真系统的碰撞检测算法［D］.天津:天津大学，2010:9－10.

［5］Gottschalk S，Lin M C，Manocha D.OBBTrees:A hierarchical structure for rapid interference detection［C］.New York:SIGGRAPH ＇96 Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques，1996:171－180.

［6］门晓鹏，吕晓峰，马登武，等.虚拟场景中基本几何元素相交测试技术［J］.海军航空工程学院学报，2006，21(3):379 －382.

［7］Devillers O，Guigue P.Faster triangle － triangle intersection tests，TR 4488［R］.［S.I.］:INRIA，2002.

［8］邹益胜，丁国富，何邕，等.空间三角形快速相交检测算法［J］.计算机应用研究，2008，25(10):2906 －2910.