General medical practice in China: evaluation of urban community health care service functions based on a rough set reduction theory

Liqing Li, Xiaojun Zhou, Zhongjie Li

General medical practice in China: evaluation of urban community health care service functions based on a rough set reduction theory

Liqing Li1, Xiaojun Zhou2, Zhongjie Li2

Objective:This study aims to achieve an empirical evaluation on the functional performances of urban community health care services in five administrative districts of Nanchang city in China.

Methods:In order to increase effectiveness, data collected from five administrative districts of Nanchang city were processed to exclude redundant information. Rough set reduction theory was brought in to evaluate the performances of community health care services in these districts through calculating key indices’ weighed importance.

Results:Comprehensive evaluation showed the score rankings from high to low as Qingyunpu district, Xihu district, Qingshanhu district, Donghu district, and Wanli district.

Conclusion:The objective performance evaluation had actually reflected the general situation (including social-economic status) of community health care services in these administrative districts of Nanchang. Attention and practical works of community health service management were needed to build a more harmonious and uniform community health care service system for residents in these districts of Nanchang.

Community health care service, Empirical evaluation, Rough set reduction theory, Redundant information, Health service management

Introduction

According to the literature, community health services provide solutions to 80% of the health problems in China [1]. The positive development of community health services is an important measure in improving the urban health service supply system, promoting health service fairness, and optimizing the allocation of health resources. China has a large population and a heavy health burden. The development of community health care, especially improvements in community health service functions, would help to ease medical care pressures in general hospitals caused by overcrowding, and improve the problems of “difficulties and high expense in medical care.” Evaluating community health service functions objectively, reasonably, and scientifically represents an important way of determining the direction of developing community health services.

Nanchang city is divided administratively into five districts (Donghu, Xihu, Qingshanhu, Qingyunpu, and Wanli); however, the development of community health services in the five districts is unbalanced. In the current study, the five districts in Nanchang were designatedas the study objects, and a comprehensive evaluation of community health service functions was performe with the aid of rough set reduction theory and the calculation of importance. This method is conducive to discovering the problems and disadvantages associated with the development of urban community health services in each district, to promote the balanced development of community health services in Nanchang and provide decision-making bases for perfecting community health service functions.

Current development status of community health services in Nanchang

The development of community health services in Nanchang has followed a similar pattern to that in the country as a whole. The community health care service dates back to 1999, and the complete framework for the community health service system was built by 2010. A survey in 2009 showed that community health services in Nanchang covered 100% of city streets and＞97.7% of community residents [2]. The setting and coverage of community health service institutions in Nanchang in 2010 are shown in Table 1.

Introduction to rough set theory

Rough set theory is a data-based reasoning method presented by Professor Z. Pawlak of Poland in 1982 [4]. According to this theory, there is no need to providea prioriinformation other than the data set to be processed. Redundant information can be deleted based on data observation, and hidden patterns and relations can be identified in the data set. Under the premise of preserving critical information, the data can be simplified and the minimum expression of knowledge can be derived. In addition, the theory is able to identify and evaluate dependencies among data, and analyze the degree of incompleteness of the knowledge, which includes the roughness, dependence among properties and importance, generation classification, and decision-making rules [4].

Principle of adopting rough set for evaluating community health service functions

The theory of rough set is built on the classification, which is considered as an equivalence relation in a particular space. The space is divided on the basis of such an equivalence. The core of rough set theory is to use a known knowledge base to approximately depict uncertain or inaccurate knowledge. This theory is characterized by the lack of need to providea prioriinformation other than the data set being processed in the problem. The description and processing of the uncertainty of the problem is thus to a certain extent objective. Given the immensity of the information system, not all information is useful. It is important to remove redundant information and preserve useful information. Similarly, not every index in a large evaluation index system is useful, and the effectiveness of empirical evaluation can be improved by removing redundant indices and preserving critical indices. In the current study, the rough set theory was incorporated into the evaluation of community health service functions. The attribute reduction method in rough set theory is used to simplify the index system. Moreover, the concept of attribute importance is used to calculate the weight of each index in rough set theory. The procedure used in the current study was as follows: determinationof the research topic; establishment of the evaluation index system; evaluation of the initial information table of indices; discretization of the initial information table; reduction of the index set; calculation of the weight of the index; calculation of comprehensive evaluation value; and sorting of evaluation results.

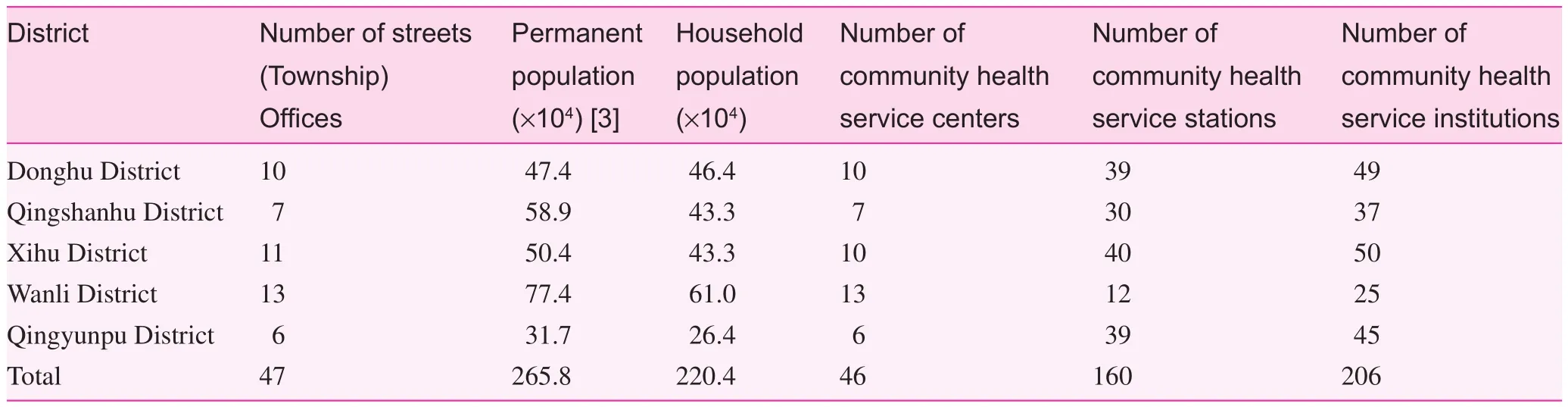
Table 1. Setting and coverage of community health service institutions of 2010 in Nanchang

Basic rough set concepts used in the study [4–6] Knowledge:Knowledge is a highly-important concept in artificial intelligence. In rough set theory, knowledge is considered as the division of the universe of discourse and an ability to classify objects. Using the concept of set, suppose U is a non-empty finite universe of discourse and R is a 2-tuple equivalence relation on U, then knowledge is the result of division on U by an equivalence relation set, R, and is denoted as U/R. The division on U by all the relations in R is defined as the knowledge base, denoted by A=(U, R). Suppose R is an equivalence relation on U, then U/R={X1,X2, …Xn} denotes a class produced by R and is called knowledge about U.

Indiscernibility relation:If P⊆W and P≠Φ, then the intersection of all equivalence relations in P is defined as the indiscernibility relation on P, denoted by IND (P): IND(P)={(x,y)∈U×U, ∀ α∈P,f(x, α)=f(y, α)}.

The indiscernibility relation is also called an equivalence relation, and divides U into a finite number of sets, which are called equivalent classes. In each equivalent set, the objects are indistinguishable. For ∀x∈U, its P equivalent class is defined as: [X]P={y∈U|(x,y)∈IND(P)}.

The family of all equivalence classes of IND (P), U/IND(P), is defined as the family-related knowledge of the equivalence relation, P, and is called P basic knowledge or basic set and denoted by U/P. Therefore, it can be seen that U/P is actually a set consisting of objects indistinguishable from each other in the universe of discourse, and is the particle composing the knowledge.

Attribute reduction:Attribute reduction is one of the core components of rough set theory. In the rough set information system, not all attributes are equally important, and some attributes are even redundant. The so-called knowledge reduction is to remove the redundant or trivial attributes under the premise of maintaining the classification ability of the information system.

Let R be an equivalence relation, andp∈R. If IND(R)=IND(R–{p}), thenpis unnecessary in R, otherwisepis essential. If eachp∈R is essential in R, then P is independent, otherwise P is dependent. Suppose P⊆R, if P is independent, and IND(P)=IND(R), then P is a reduction of R.

Calculation of attribute importance based on amount of knowledge information:The amount of information is used to describe the data sets in the universe of discourse. The rows in the information table represent objects, and the columns represent attributes. Each attribute corresponds to an equivalence relation.

Suppose A=(U, R) is an information system. For an equivalence relation P⊆R, there is classification U/IND(P)={X1,X2, …,Xn}. Then, the amount of information of P is denoted by

The |*| represents the cardinal number of the set, i.e., the number of elements in a set. The importance of an attribute (attr) in an attribute set, P, is defined as follows:

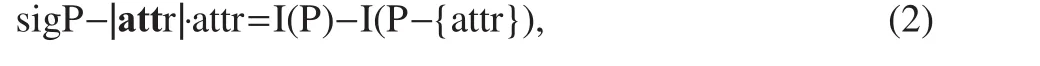
where attr denotes a certain attribute, and P⊆R is an equivalent subset in the equivalent set, R. Each attribute importance in the attribute set is normalized to obtain the weight of each attribute:

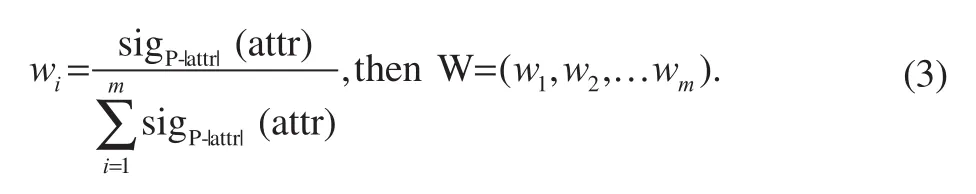
Empirical evaluation of community health service functions in Nanchang

The community health service is an effective, economical, convenient, integrated, and continuous grassroots health service provided by the health service institutions in Chinese cities, with the community as the basic unit. The service covers disease prevention, medical treatment, health care, rehabilitation, health education, and family planning guidance. The current study established an evaluation index system covering these six functions based on the actual development status of urban community health services in Nanchang, as shown in Table 2.

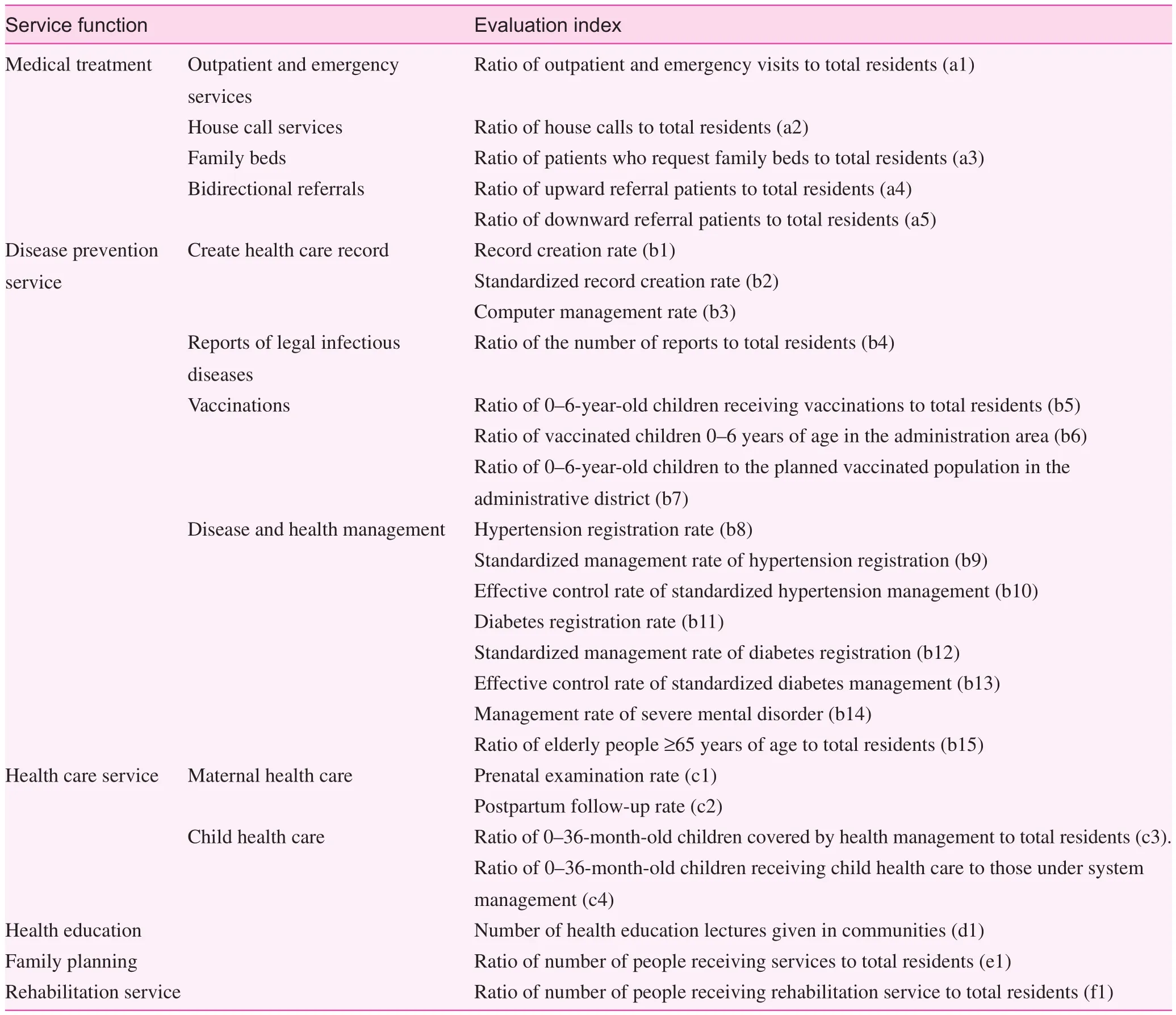
Table 2. Evaluation index system for community health service functions in Nanchang

Setting of evaluation index information table

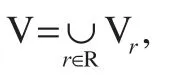
The setting of the evaluation index information table refers to the collection of sample index data and the corresponding discretization processing. That is, to fill the decision-making table with the obtained actual data or discretized data. The collection of sample index data is the key process. In the current study, the census method was mainly used to investigate thecurrent situation of the health care institutions. The specific assignments of indices are shown in Table 3. The districts are denoted by Si (i=1, 2, 3, 4, 5), where S1 is Donghu District, S2 is Qingshanhu District, S3 is Xihu District, S4 is Wanli District, and S5 is Qingyunpu District.

All the data types in Table 3 were fixed-distance data. However, the rough set method, the core of which is the indiscernibility relation presented by Pawlak, is used to process discrete attribute values. In the current study, the method of grouping by distance was used for data discretization. In actual grouping, the empirical formula presented by Sturges [7] can be used to determine the group number, K: K=1+lgn/lg2, wherendenotes the number of data. The round-off result is the theoretical number of groups. The distance between groups can be calculated by the following equation: distance=(maximum–minimum)/group number [7]. The group number, K, is set as 3 by taking the requirement of practical problem solving into consideration. The discretized information is shown in Table 4.

Reduction of index set

The cyclic column reduction method with indiscernibility relation was used to reduce the evaluation indices of the six functions. The obtained reduction results of the five indices on medical services were {a3, a4, a5}. When reducing the indices of disease prevention service, the key indices amongthe indices in the lower level were determined first, because there were many indices in the lower level i.e., to reduce all the indices of the creation of health records, vaccinations, and disease prevention and health management. The reduction results were {b1}, {b5}, and {b12, b15}, respectively. Therefore, the key index on the creation of health records were b1, that of vaccination was b5, and those of disease prevention and health management were b12 and b15, respectively. Thus, the key indices of disease prevention services were {b1, b5, b12, b15}. Another reduction was then performed, and the reduction result was {b12, b15}. The reduction result of health care services was {c2, c4}. There was only one index for health education, family planning and rehabilitation services, hence there was no need for reduction. As a result, the simplified evaluation indices that maintain the same classification ability are shown in Table 5.

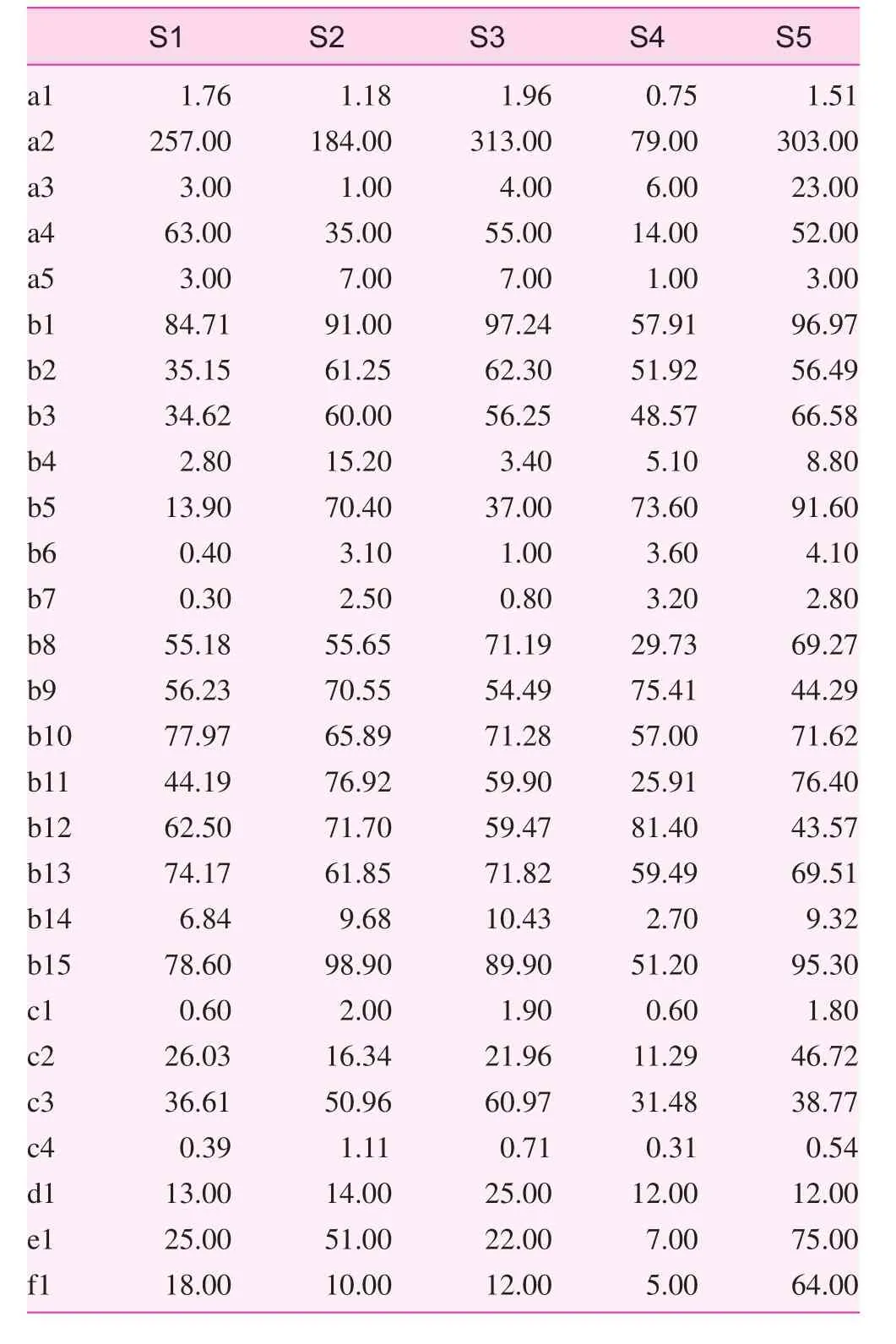
Table 3. Value assignments in community health service function evaluation index system for Nanchang

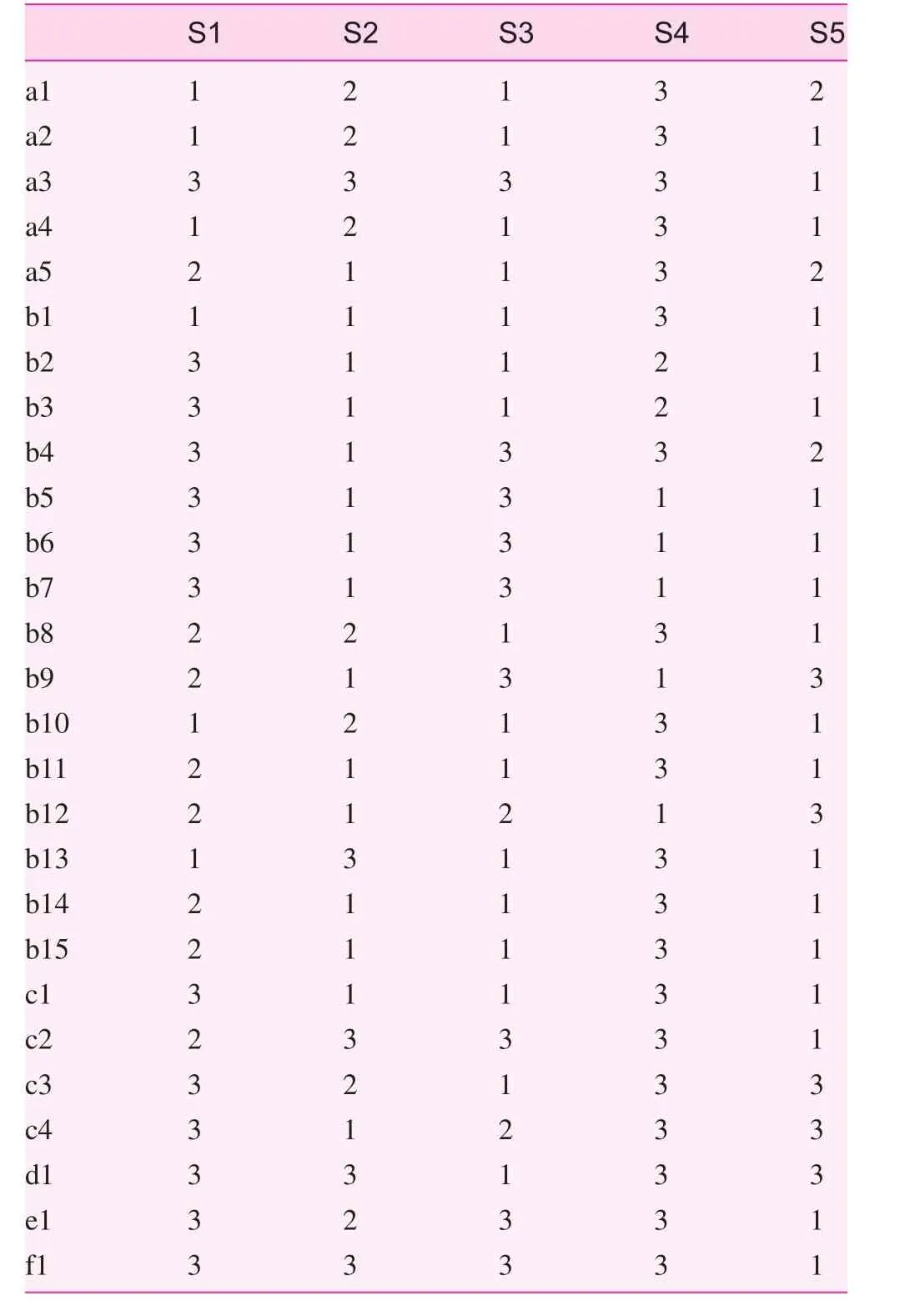
Table 4. Discretization information

Calculation of attribute importance and weight of the indices

The attribute importance and weight of each evaluation index was calculated, based on the reduction results [8].

First, the attribute importance and the weight of the medical service index was calculated. After attribute reduction, the simplified index set was P={a3, a4, a5} and P⊆R. By the property of reduction, there was U/IND(P)=U/IND(R). Based on the method of calculating attribute importance using the amount of knowledge information presented in rough set theory, the importance of each index, SP(ri)(i=1, 2, …,m), was calculated. The division of the universe of discourse U by the equivalence relation P was as follows: U/IND(P)={{S1}, {S2}, {S3}, {S4}, {S5}}. After removing a3, the division of the universe of discourse by the equivalence relation was U/ IND(P–{a3}), as follows: {{S1, S5}, {S2}, {S3}, {S4}}. The amount of information of P was calculated according to Eq. (1):

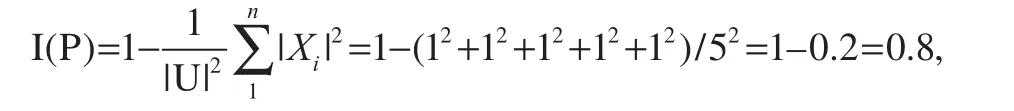
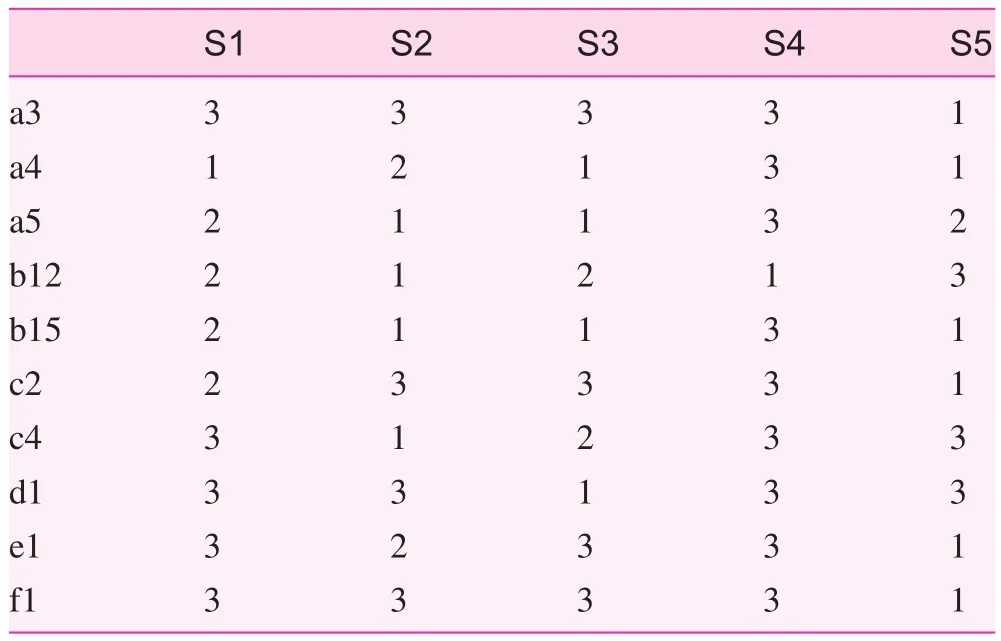
Table 5. Decision-making table after reduction

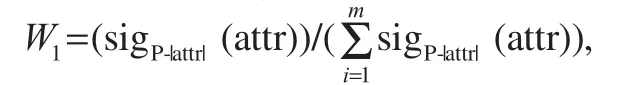
Similarly, the attribute importance and weight were calculated for indices of disease prevention and health care services, as shown in Tables 7 and 8.

There was only one index for health education, family planning, and rehabilitation services, and there was therefore no need for reduction, and normalization was sufficient.

Calculation of comprehensive evaluation value

According to the weight of each index after reduction, the scores of each index of the medical treatment services for thefive districts in Nanchang were calculated. The calculation was performed by multiplying the index weight by a 3*5 normalized matrix formed by the 3 indices (original data). In this way, the comprehensive evaluation value of medical treatment service was obtained asAi(i=1,2, …, 5).

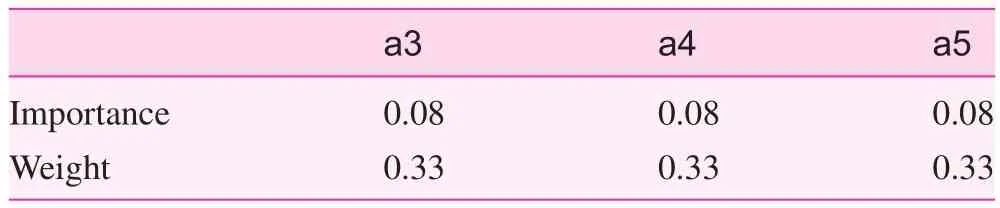
Table 6. Importance and weight of indices of medical treatment services

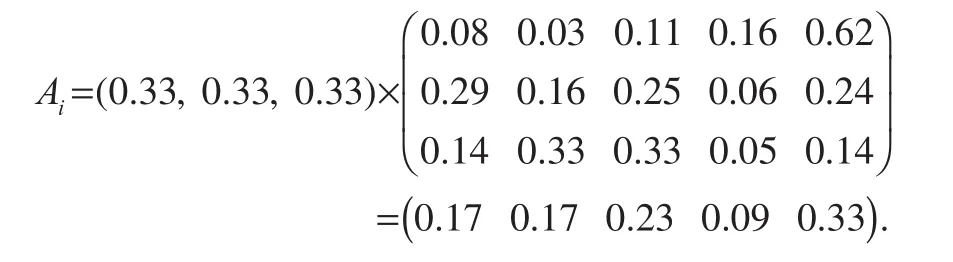
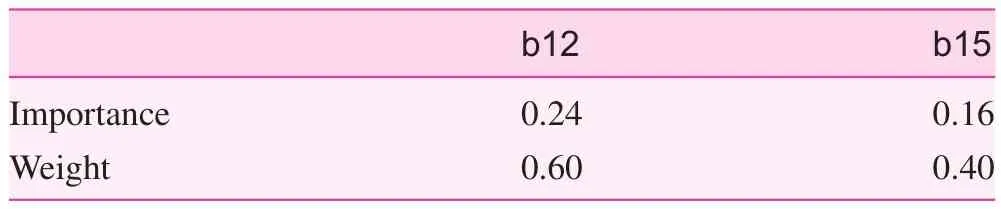
Table 7. Importance degree and weight of indicators of preventive services

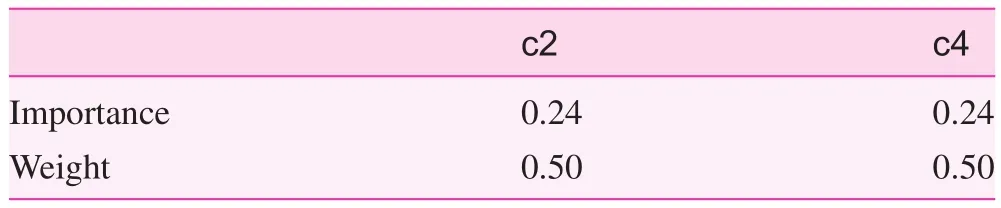
Table 8. Importance and weight of indices of health care services

Similarly,BiandCiwere calculated.

The evaluation results for the six major health care services of the five districts in Nanchang were obtained, as shown in Table 9.

It was easy to obtain the evaluation scores of the community health service functions in the five districts in Nanchang from the above results. However, the final evaluation results could not be obtained simply by addition, because the weight of each function was different. Thus, according to expert consultation and scoring, the weights of the six functions were determined as 0.21, 0.27, 0.24, 0.15, 0.03, and 0.09. The final total evaluation values of S1, S2, S3, S4, and S5 were 0.17, 0.20, 0.22, 0.13, and 0.27, respectively.

Discussion

The greatest advantage of the rough set method lies in mining the potential information from a data set withouta prioriknowledge. The obtained data were close to the truth and objective, compared with other approaches. In the current study, the weight of each evaluation index was obtained according to the information amount for each attribute in the rough set, so that the subjectivity of the traditional weightdetermination method was overcome. The evaluation results were made more objective and accurate by combining the linear-weighting method. An evaluation index system was built covering the six functions of urban community health services. The reduction approach was borrowed from the rough set theory to perform an empirical evaluation, and a ranking of the comprehensive evaluation scores of the community health service functions of the five districts in Nanchang was obtained. Because the original data were subject to normalization, the influence of index dimensionality was eliminated. The information of the original data was fully reflected in the ranking result. The advantages and disadvantages of different evaluation units were quantified in a direct and reliable manner, with practical significance for theharmonic development of urban community health services in Nanchang.

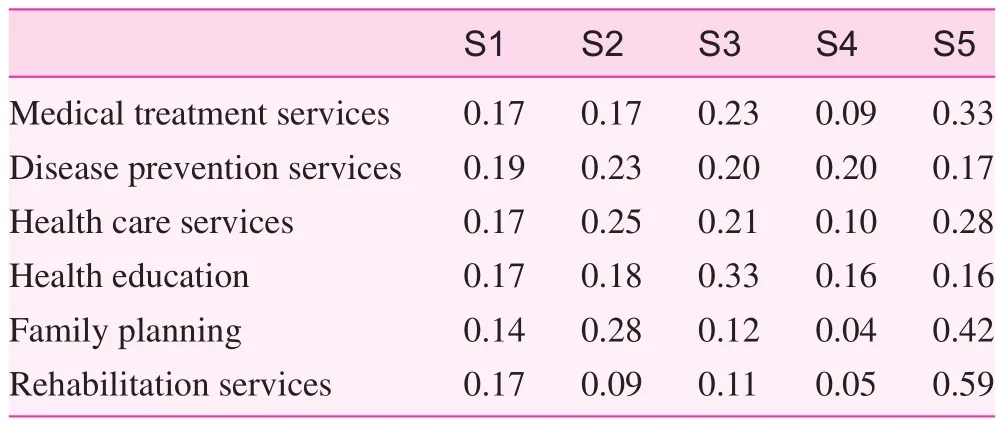
Table 9. Evaluation of six major community health service functions in five administrative districts of Nanchang

According to the results of this study, the ranking of the five districts in Nanchang in terms of the community health care service functions was as follows: Qingyunpu District; Xihu District; Qingshanhu District; Donghu District; and Wanli District. This ranking conforms to the current development status of community health care services in Nanchang. The medical treatment services, rehabilitation services, family planning, and health care services provided by the community health care service institutions in Qingyunpu District were better than in the other four districts. Qingyunpu District is relatively far from the downtown area of Nanchang, where most general hospitals are located. Numerous pillar industries are based in Qingyunpu District. The national economy in this district is continuously expanding in volume. The district government already pays close attention to livelihood issues, and attaches great importance to the development of community health care services. Wanli District ranks last, primarily for geographic reasons. This district is in the suburbs, and the construction of municipal infrastructures and its economic and social developments fall far behind those of the other four districts. Medical health care services need to be improved in this district.

Conflict of interest

The authors declare no conflict of interests.

1. Li Y, Feng X. The study on evaluation indicator system of the performance of community health services Chinese. Appl J Gen Pract 2011;9:951–3.

2. Li Z. Community health service status and synthetic evaluation research in Nanchang. China: Nanchang University; 2012.

3. Nanchang Bureau of Statistics. Announcement of main data of the sixth nationwide population census in Nanchang, 2010. Available from: http://www.nctj.gov.cn/News. shtml?p5=22447.

4. Pawlak Z. Rough sets – Theoretical aspects of reasoning about data. Dordrecht: Kluwer Academic Publishers; 1991.

5. Hu S, He Y. Rough set theory and its applications. Beijing: Beihang University Press; 2006. pp.1–14.

6. Liu Q. Rough set and rough reasoning. Beijing: Science Press; 2001. pp. 1–66.

7. Xue W. Data analysis based on SPSS. Beijing: China Renmin University Press; 2006.

8. Li L, Liu W. An evaluation model of patient satisfaction degree based on rough set and its empirical analysis. Math Pract Theory 2009;39:25–30.

1. School of Economics and Management, Jiangxi Science & Technology Normal University, Nanchang 330031, Jiangxi Province, China

2. School of Public Health, Medical College of Nanchang University, Nanchang, China

Xiaojun Zhou

School of Public Health, Medical College of Nanchang University, Nanchang 330006, Jiangxi Province, China

E-mail: zxj12zxj@sohu.com

Funded by the National Natural Science Foundation of China in 2011 (71163016) and the Technology Project of Provincial Education Department of Jiangxi in 2013 (GJJ13559).

16 October 2013;

Accepted 17 December 2013