基于直驱永磁同步风力发电系统的控制器设计与研究

倪 瑶，孙黎霞

（河海大学 能源与电气学院，江苏 南京 211100）

常规能源资源有限，而且造成了严重的大气污染。风能是一种可再生的清洁能源，资源丰富，发电成本较低。因此，风力发电受到了世界各国高度重视。由于直驱型永磁同步风力发电系统机械损耗小，运行效率高，机组噪声小，正逐渐得到人们的青睐。

直驱永磁同步风力发电系统机侧变流器影响着系统输出有功功率的能力，电网侧变流器则直接影响系统输出的电能质量。因此，对变流器的控制是整个风力发电机组中最重要的控制内容之一。解耦控制策略被广泛应用于控制系统有功和无功，该控制策略是一种基于PI控制器的控制策略，有控制性能好、可靠性高等诸多优点。本文通过对直驱永磁同步风力发电系统进行数学建模，并提出基于粒子群算法来解决永磁同步风力发电系统PI参数的设计优化。

粒子群算法，又称为粒子群优化算法 （Particle Swarm Optimization），简称PSO算法[1]，同遗传算法类似，是一种基于迭代的优化算法。系统初始化一组随机解，通过多次迭代搜寻最优值。这种算法因为容易实现、精度高、收敛快等优点引起了学术界的重视，并且在解决实际问题中展示了其优越性。文中在风速突变时，对粒子群算法PI参数优化前后直驱永磁同步发电系统进行仿真对比。仿真结果验证了该方法应用于风力永磁同步发电系统的有效性。

1 直驱永磁同步风力发电系统的建模

直驱永磁同步风力发电系统包括如下几个基本组成部分：风力机、发电机、整流器、逆变器、控制系统等。并网逆变器是工作于逆变状态的PWM整流器，其数学模型与PWM整流器相同，控制策略也相似。文中详述永磁同步风力发电系统的机侧PI控制器设计与优化。直驱永磁同步风力发电系统的基本结构如图1所示。

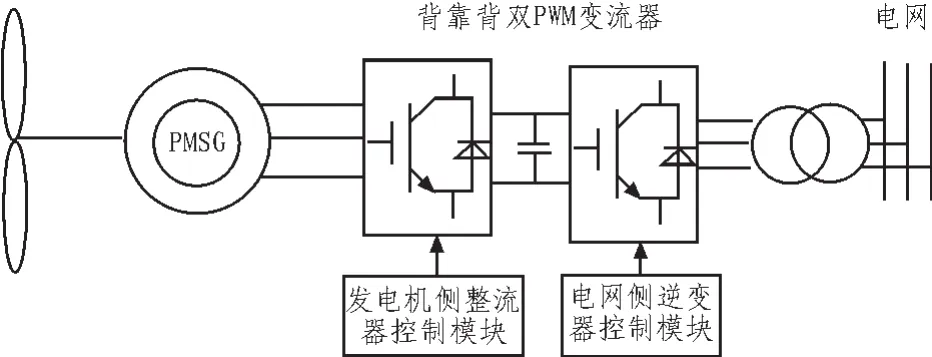
图1 直驱永磁同步风力发电系统模型Fig.1 Configuration of wind power generation system with D-PMSG

1.1 风力机模型

风力机的输出功率与风速的关系为：

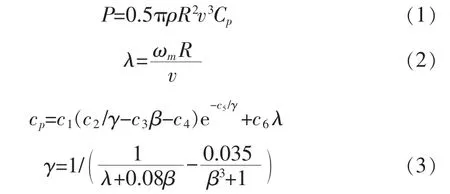
式中，ρ为空气密度；v为风速；R为风力机转子半径；Cp为风能利用系数；λ为叶尖速比；ωm为风力机的角速度；c1=0.517 6，c2=116，c3=0.4，c4=5，c5=21，c6=0.006 8。

1.2 永磁同步发电机数学模型

永磁同步发电机在三相坐标系下的电压方程是一组变系数微分方程，为了便于分析，通常采用坐标变换的方法，将变系数微分方程等效变换为常系数微分方程以便求解。为了下文满足矢量控制的需要，变换时将d-q坐标系的d轴与转子磁场轴线重合[2]。永磁同步发电机数学模型如下：

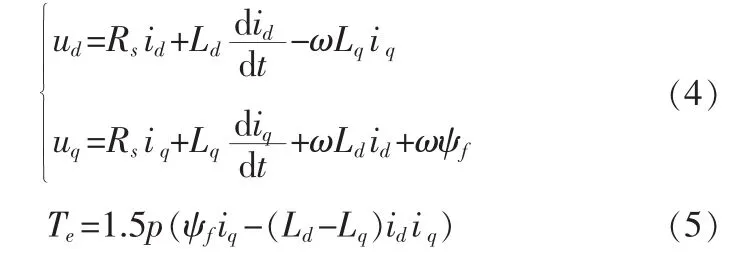
直驱风力发电机组的传动系统数学模型为：

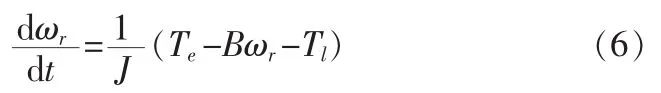
式中，ud、uq分别为定子 d、q 轴电压分量；id、iq分别为定子 d、q 轴电流分量；Rs为定子电阻；Ld、Lq分别为定子 d、q 轴自感；ωr为转子角速度，ω=pωr为转子电角速度；ψf为转子永磁体的磁链最大值。Tl风力机产生的驱动转矩，Te发电机的电磁转矩；J为转动惯量；B为摩擦系数；p为电机极对数。

2 基于MPPT的系统控制器设计

2.1 直驱永磁同步风力发电系统控制目标

风力机将捕获的风能转换为机械能来驱动永磁同步发电机，根据公式（1）～（3）对于固定的桨距角β来说，一定存在最佳叶尖速比λopt和最大风能利用系数Cpmax。永磁同步风力发电系统控制目标：机侧控制为了获得最大风能输出，必须对发电机输出功率进行控制，使其在风速变化时，跟踪最大功率点P*，从而保持最佳叶尖速比λopt不变[3]。网侧控制功率因数为1。

2.2 PMSM双闭环磁场定向控制器设计

以面装式永磁同步电机为研究对象，其交、直轴电感相等 Ld=Lq=L，则式（2）为：

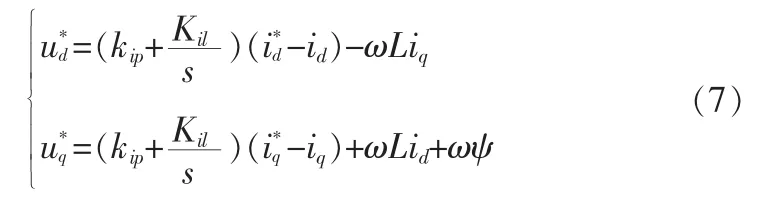
根据式（7）可得永磁同步发电机机侧变流器的电流环控制框图，根据矢量解耦控制原理[4]，在发电机的电流环控制中，要对直轴电流和交轴电流分别进行闭环比例积分（PI）控制，从而得到相应的控制电压分量u′d和u′q，还要分别加上交叉耦合电压的补偿项-ωLiq、ωLid+ωψ的影响，最终分别得到直轴控制电压u*d和交轴控制电压u*q。由于跟踪最大功率点P*的要求，外环为有功功率控制环的设计。PMSG磁场定向的双闭环控制如图2所示。

图2 PMSM磁场定向的双闭环控制Fig.2 Field oriented double close-loop control in the PMSM system

2.3 工程化的PI参数设计

图3所示的永磁同步发电机电流、功率双闭环控制系统是一种多环系统，设计多环系统的一般方法是：从内环到外环进行设计，先从电流环开始，设计好电流调节器，然后把电流环看作是功率环的一个部分，再设计功率环，因此首先考虑进行电流环的设计实现。本节采用经验试凑法整定PI控制器参数，设计过程如图3所示。

图3 经验试凑法流程Fig.3 Process of manual tuning

直驱永磁同步风力发电系统仿真模型如图4所示。

3 基于粒子群算法的PI控制器参数优化

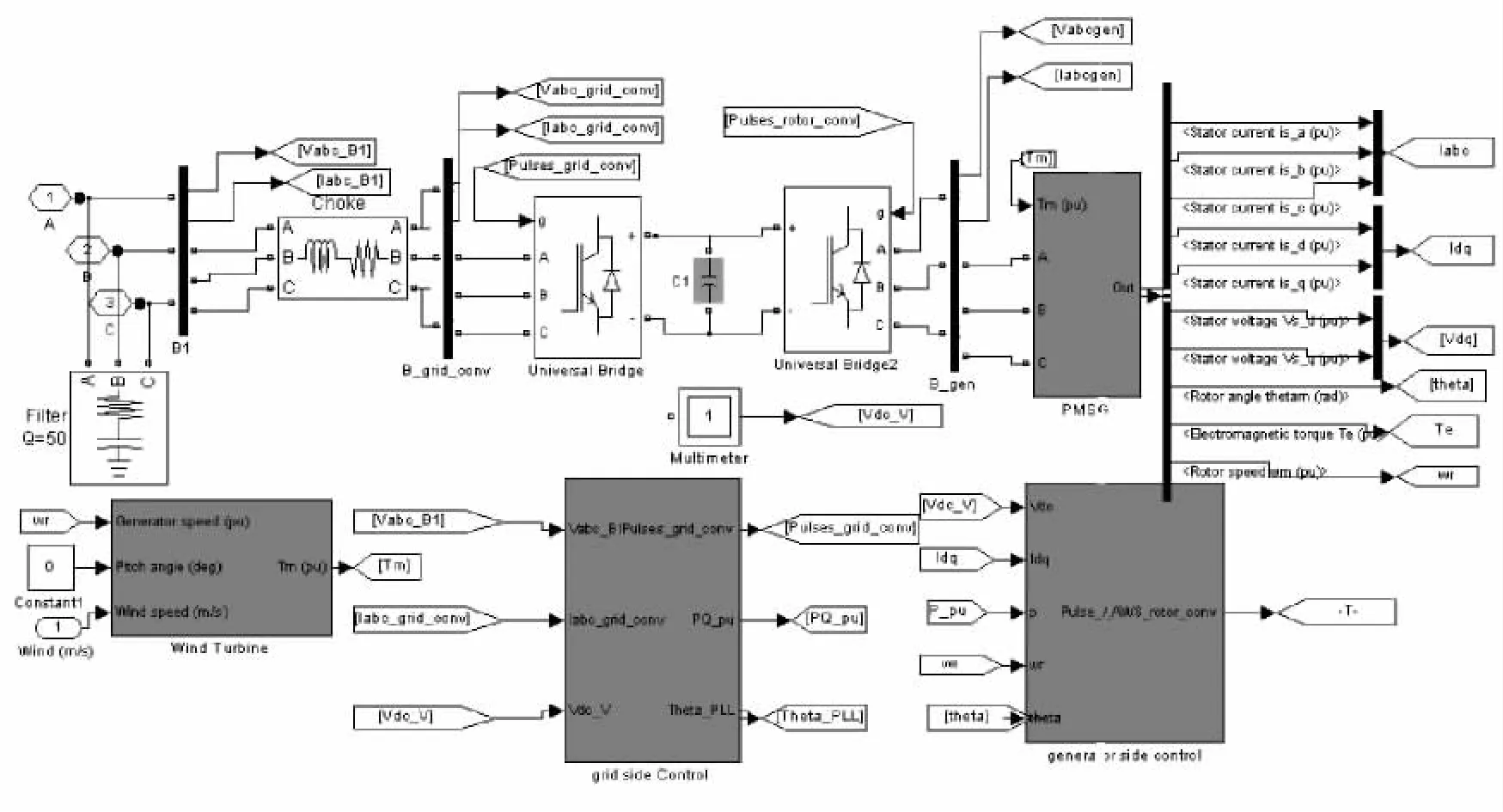
图4 系统仿真模型Fig.4 Simulation model of PMSG system

在粒子群算法中，每个优化问题都可以想象成m维空间上搜索的一个点，这些点被称之为粒子，共有n个粒子组成一个群体。该算法首先初始化得到一群随机粒子 （随机解），然后通过多次迭代得到最优解。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己，第一个极值就是粒子本身所找到的最优解，这个解叫做个体极值Pbest；另一个极值是整个种群目前找到的最优解，这个极值是全局极值[5]gbest。在第t+1次迭代计算时，粒子i根据以下公式来更新自己的速度和位置，由于粒子位置更新，从而产生了新的种群xik（t+1）：

式中，ω是惯性权重；c1、c2是学习因子；r1和 r2为 0到 1之间的随机数；k=1，2，...，m 为粒子的大小；v 是粒子的速度；x是粒子的位置。

直驱永磁同步风力发电系统的PI参数优化步骤[6-7]：

1）算法参数设定：实测发电机输出的有功功率P的轨迹和数值；设置种群大小为20，粒子大小为6（要辨识6个PI控制参数）；最大迭代次数50次；设定6个PI参数的搜索区域。权系数 ωmax=0.9，ωmin=0.4；学习因子 c1=c2=2；初始化种群，随机产生由20个粒子组成的初始种群，随机产生粒子的位置和速度。

3）更新粒子当前最优极值：比较粒子的当前适应值F（xi）和自身历史最优值 pbest，如果 F（xi）优于 pbest，则置 pbest为当前值F（xi），pbest对应的位置为当前这个粒子的位置。并更新pbest对应的粒子6个PI参数。

4）更新种群当前最优极值：比较粒子当前适应值F（xi）与种群最优值 gbest，如果 F（xi）优于 gbest，则置 gbest为当前值 F（xi），gbest对应的位置为当前这个粒子的位置。

5）根据公式（8）～（9）更新当前粒子的速度和新的位置。

6）有时更新粒子位置可能会超出搜索范围，此时，可以将其强制限制在临近的搜索边界上。

7）检查结束条件，如果满足，则优化算法寻优结束。否则，t=t+1，当前迭代次数加1，转至步骤2）结束条件为：①寻优次数达到最大迭代次数50；②适应度函数值小于给定值。

基于粒子群的永磁同步风力发电系统的PI控制器参数优化算法流程如图5所示。

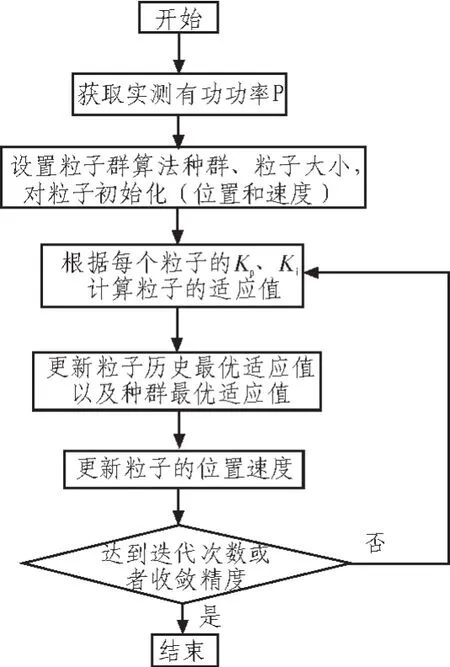
图5 PI参数优化算法流程图Fig.5 Process of PI Parameter optimization

4 仿真分析

4.1 系统仿真结果

文中在MATLAB/SIMULINK环境下搭建了一台1.5 MW直驱永磁同步风力发电系统，风速在2 s时从8 m/s突变到12 m/s，系统仿真结果如图6所示。

4.2 参数优化

由于文中是基于matlab仿真建模无法得到工程实测有功，所以将仿真模型输出的有功功率当作实测值即目标曲线。在输入风速的突变下，用输出有功功率受到扰动的效果来激发控制系统的动态性能，从而辨识得到控制器各参数值。系统采用粒子群优化算法后，功率控制外环kp1、ki1，直轴电流控制内环kp2、ki2，交轴电流控制内环kp3、ki3参数如表1所示，有功功率仿真如图7所示。

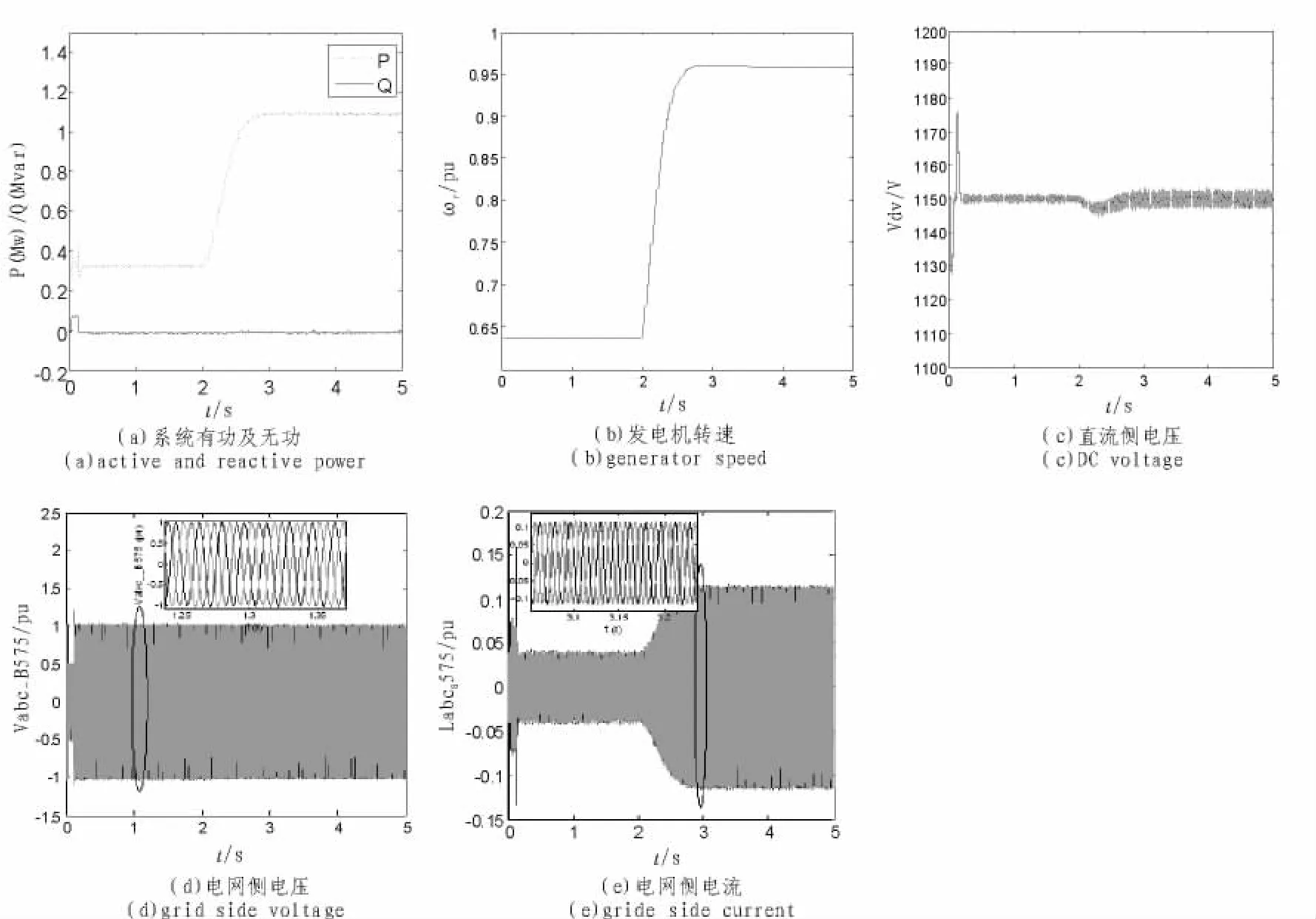
图6 直驱永磁同步风力发电系统仿真波形Fig.6 Simulation waveforms

表1 粒子群算法辨识参数Tab.1 Particle swarm algorithm identification parameters

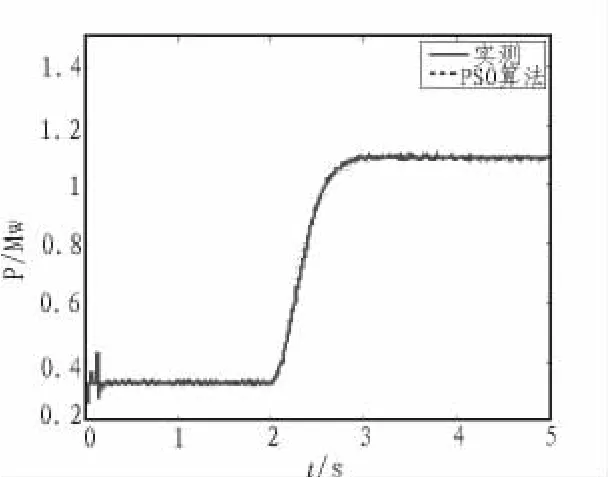
图7 PSO参数优化仿真图Fig.7 PSO parameter optimization simulation diagram

由图7可知，采用粒子群优化方法辨识出的有功功率曲线能够较好拟合于目标曲线，误差小，其反映出的动态特性更加接近于系统真实情况。基于上述可知，粒子群优化算法用于直驱永磁同步风力发电系统控制器参数优化是有效可靠的。

5 结 论

文中对直驱永磁同步风力发电系统进行建模分析，并采用经验试凑法设计出系统PI控制器参数。提出基于粒子群优化算法的PI参数优化设计，仿真结果表明在风速突变后，经过粒子群优化算法后的直驱永磁同步发电系统输出的有功功率能够很好地拟合真实值，跟踪风速扰动，动态响应更快，进而验证了该方法的工程应用性。

[1]王克华，牛慧.一种参数自适应调整和边界约束的粒子群算法[J].电子设计工程，2011，19（21）:46-52.

WANG Ke-hua，NIU Hui.Particle swarm optimization with adaptive parameters and boundary constraints[J].Electronic Design Engineering，2011，19（21）:46-52.

[2]王成元，夏加宽，杨俊友，等.电机现代控制[M].北京：机械工业出版社，2006.

[3]尹明，李庚银，张建成，等.直驱式永磁同步风力发电机组建模及其控制策略[J].电网技术，2008，31（15）:61-65.

YIN Ming，LI Geng-yin，ZHANG Jian-cheng，et al.Modeling and control strategies of directly driven wind turbine with permanent magnet synchronous generator[J].Power System Technology，2008，31（15）:61-65.

[4]Yongbin Li， Mi，C Analysis.Design and simulation of directdrive PM wind power generators with PWM rectifiers[C]//Industrial Electronics Society，2007.IECON 2007.33rd Annual Conference of the IEEE，2007：1610-1614.

[5]张洪涛，胡红丽，王斌.一种改进粒子群算法及其在PID参数整定中的应用[J].控制理论与应用，2008，27（12）:14-16.

ZHANG Hong-tao，HU Hong-li，WANG Bin.A modified PSO algorithm and its application in tuning of PID[J].Control Theory and Applications，2008，27（12）:14-16.

[6]杨林立，张萍.基于粒子群算法双馈风力发电系统PI参数优化[J].微计算机信息，2010，26（11）:154-156.

YANG Lin-li，ZHANG Ping.The doubly-fed wind power generator system PI parameter optimization based on particle swarm optimization algorithm[J].Microcomputer Information，2010，26（11）:154-156.

[7]张家骏.基于粒子群算法的PID控制器参数优化研究[J].计算机仿真，2010，27（10）:191-193.

ZHANG Jia-jun.Optimization parameters of PID controller parameters based on particle swarm optimization[J].Computer Simulation，2010，27（10）:191-193.