矩阵变流器的控制策略研究

韩竺秦

（韶关学院物理与机电工程学院，广东韶关 512005）

1 引言

目前的交流变频调速系统、电力系统大多都采用不控整流或传统PWM交-直-交电压型电力变流器，导致交流侧电压和电流波形很差，功率因数低，这对于发电机组的稳定运行极为不利。目前，矩阵式变流器在中高压变频调速、电力系统无功补偿和风力发电等领域得到了广泛研究。矩阵式变流器无中间直流环节，结构紧凑、体积小、效率高，便于实现模块化。降低生产成本的需求促使新型的电力变换器来替代原有的传统电力变换器,而矩阵式变换器正是适应这种全新要求的电力装置。

2 矩阵式变换器原理分析

矩阵式变换器是一种直接AC-AC变换器［2］。它能实现能量的双向流动，矩阵式变换器中的开关器件在关断状态下承受的电压可能是反向的，也可能是正向的，所以，开关器件一定要采用双向开关器件［1］。

三相-三相交流矩阵式变换器中的每个双向开关可用开关函数Sij表示，定义如式（1）。

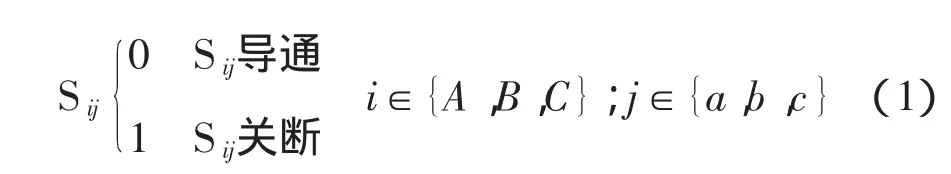
矩阵式变换器在运行过程中必须满足三相输入端中任意两相之间不能短路，避免使电压源短路造成过电流；三相输出端任意一相不能开路，函数表示为式（2）。

在矩阵式变换器电路中，没有续流二极管，没有电流的自然续流通路，使得开关器件直接的换流比传统的背靠背变频器困难。矩阵式变换器的换流控制，必须严格遵守上面提到的两个条件。基于电流方向检测的四步换流策略得到广泛的应用，从双向Sa切换到双向开关Sb。开始假定开关a中两个IGBT管都导通，第一步，关断IGBT管San，因为没有负载电流，也就是负导通部分。第二步，打开IGBT管Sap，使开关b有电流流过，两个开关a和b只流过正电流是可以避免短路的。依靠的是瞬时输入电压，第二步后，二极管承受的电压Vab，如果Vab<0，则二极管反向偏置和发生自然换向。如果Vab>0，将发生强制换向。第三步，关断IGBT管Sap，就是正向导通部分。第四步，打开IGBT管Sbn，负导通部分。这就完成了两个开关之间的换流。

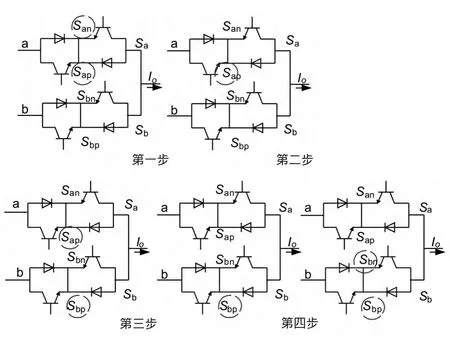
图1 四步换流顺序

四步换流成功地构成了对两个开关的换流控制，即阻止了可能使电源发生短路的开关组合，又保证了在任意时刻给负载提供至少一条路径。

3 矩阵式变换器的控制策略

矩阵式变换器包含开关多，数学模型复杂，控制繁琐，在矩阵式变换器的应用中，应用合适的控制策略，以确保系统稳定可靠的运行。本文主要讨论间接矢量调制法。

间接调制的目标是由输入电压合成输出电压，输出电流合成输入电流。三相矩阵式变换器可以由3×3的矩阵来描述，从输入相到输出相由9个双向开关连接，中间没有任何储能元件，因此，输出电压和输入电流可以有传递函数T或T的转置TT来表示。

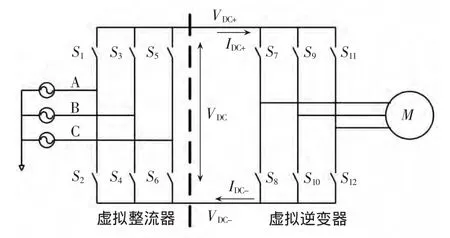
图2 间接调制的等效电路

间接空间矢量（Indirect SVM）、矩阵式变换器的等效电路描述如图2所示，电流源整流和电压源逆变，中间有一个虚拟的中间直流环节，逆变侧有一标准的三相电压源逆变器的拓扑结构，由6个开关（S7-S12）组成。整流器侧有相同的电力拓扑结构，由另外6个开关（S1-S6）组成。整流和逆变阶段通过虚拟直流环节直接连接。通过分离矩阵式变换器的传递函数T，如式Vo=T×VI中的T，得到整流器和逆变器的传递函数T=I×R。

矩阵I为逆变器传递函数，矩阵R为整流器传递函数，这种方式给矩阵式变换器提供了模型基础，把矩阵变换器当作背靠背PWM变换器（没有任何直流的储能环节）。这就是众所周知的空间矢量PWM调制策略，电压源型逆变器（变频器）或PWM整流器可以用在矩阵变换器中。

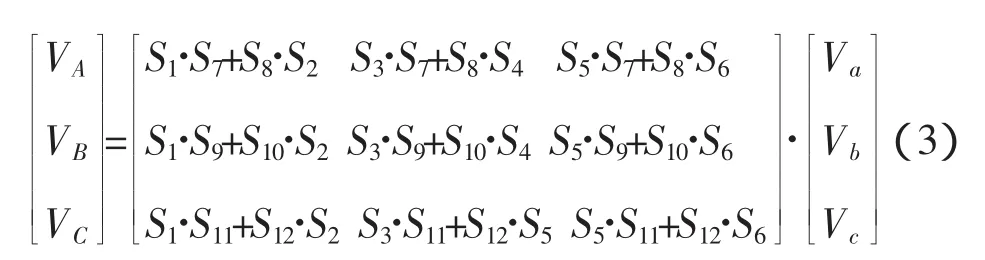
上述矩阵可以看出，输出阶段是输入相逆变器开关S7-S12和整流器开关S1-S6的乘积和的混合，式（3）的第一行表示从输入的a、b、c相如何输出A相以及它的数学表达式。如果等效电路可以看作是由逆变输出A相，A相的半桥开关S7和S8通过6个整流开关直接链接到输入相a、b、c相。

图3 A相转换的等效电路

如图3所示显示了设置等效电路的开关使其转化为矩阵变换器相关的9个双向开关的开关设置的情况，以A相为例，给出了一个基本思想，即通过矩阵变换器的占空比可以通过乘以相应等效电路中的整流和逆变开关的占空比。

因此，矩阵式变换器的间接调制技术可以应用众所周知的空间矢量PWM的整流以及逆变阶段。下面介绍两个独立的空间矢量调制的电流源整流和电压源逆变，然后两个调制相结合，调制的矩阵式变换器。下面分别就虚拟整流器和虚拟逆变器进行研究。

逆变部分可看作为一个独立的电压源逆变器提供直流电压源，VDC＝VDC+-VDC-，如图4所示。

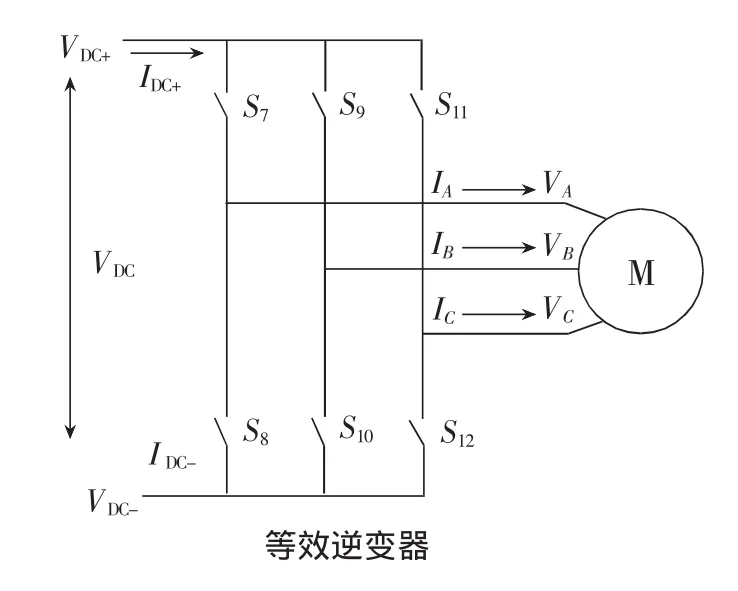
图4 等效的虚拟逆变器电路

输出电压可表示为虚拟直流环节电压VDC乘以逆变阶段开关状态，逆变器传递函数矩阵I，同时，直流电流IDC可以通过转置矩阵IT得到。

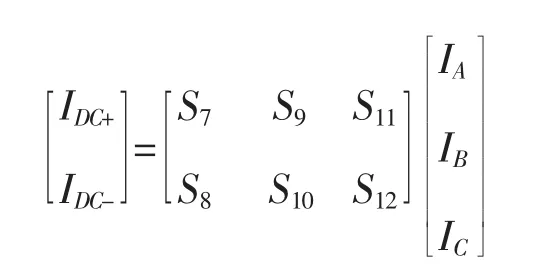
那么输出电压空间矢量和输出电流的空间矢量为：

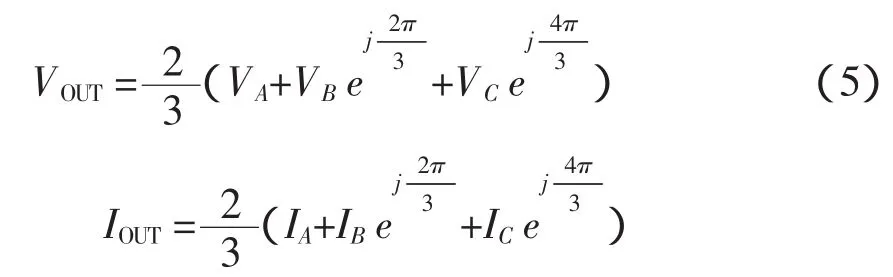
该虚拟逆变器开关，S7-S12只能有8个允许组合的方式，以避免短路电流通过三个半桥。这8个组合可分为6个非零电压输出，是正矢量V1-V6和两个零输出电压，是零矢量和V0。

电压空间矢量V1［100］表明，输出相VA连接到直流母线正极VDC+，另一相链接到VB，VC链接到直流母线的负极，其向量幅度的计算如式（6）所示。

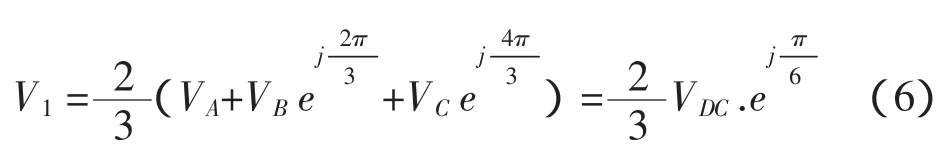
离散的7个空间矢量在复平面内可以构成一个六边形，如图5所示。通过7个离散的电压空间矢量V0-V6和可以合成六边形任意输出电压Vout。

图5 逆变阶段电压六边形空间矢量

输出电压的平均值和直流环节电流可以如式（7）表示。

虚拟整流器和逆变阶段相类似，输入电流的平均值和直流环节电压如式（8）表示。

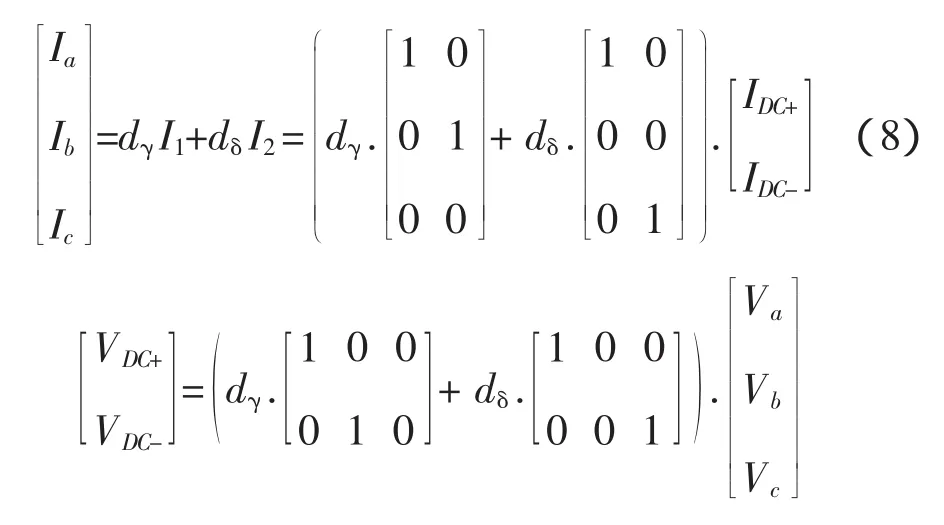
4 矩阵式变换器的间接空间矢量调制

上述内容所提到占空比和有关开关矢量来自虚拟整流和虚拟逆变器，只是在矩阵式变换器下的等效电路下有意义。因此，9个双向开关矩阵变换器的两个独立的空间矢量调制应该合并成一个调制方法，本节讨论矩阵式式变换器开关状态整流器和逆变器阶段如何转化为相应的开关状态。

矩阵式变换器同时输出电压和输入电流的向量（SVM）可以通过采用虚拟逆变SVM的两个虚拟直流母线之间的电压幅值整流（SVM）。虚拟直流环节电压VDC是通过两个输入线电压和输入电流矢量Iγ和Iδ，在dγ和dδ间，然后，两个输出电压矢量Vα和Vβ适用于合成所需要期望的输出电压。当Vα和Vβ应用于第一次电流矢量Iγ时，两个新Vα的矢量，Vα-Iγ和Vβ-Iγ，新矢量空间的占空比变成dαγ和dβγ，下面分别给出了dαγ和dβγ的定义。当Vα和Vβ应用于第二个电流矢量Iδ时，产生两个新的矢量，Vα-Iδ和Vβ-Iδ，新矢量的占空比为dαδ和dβδ。下面分别给出了dαδ和dβδ的定义。这四个新的空间矢量占空比可作为现逆变器的占空比如式（9）所示。

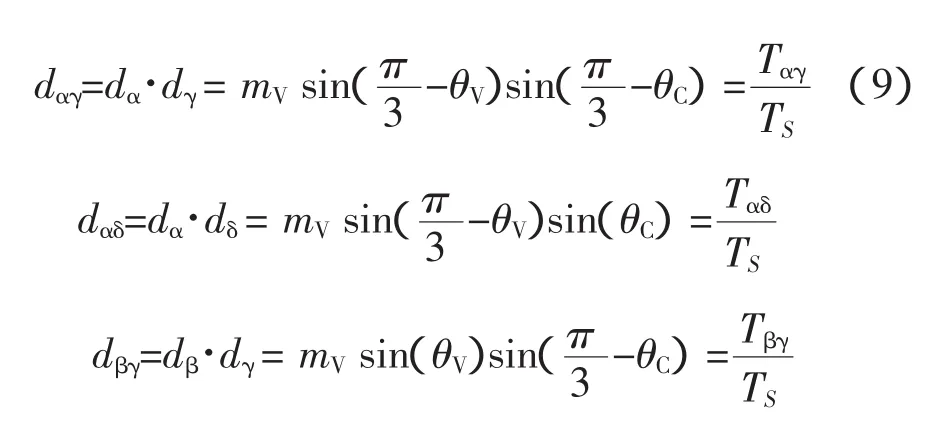
在余下的部分开关转换TS，零向量的应用如式（10）。

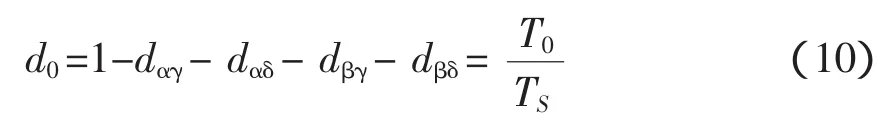
输出线电压等于零。这三个零矢量组合，是[aaa]、[bbb]和[ccc]，可以以相同的输入端连接所有三个输出端。在零矢量作用期间，所有输入电流为零，输出的负载电流是自由通过矩阵变换器开关的。

因为逆变器和整流器的六边形都包含了6个扇区，有6×6=36的组合或运作模式。例如，输出参考电压输入电流在特定瞬间都位于扇区S0，输出电压可直接合成。

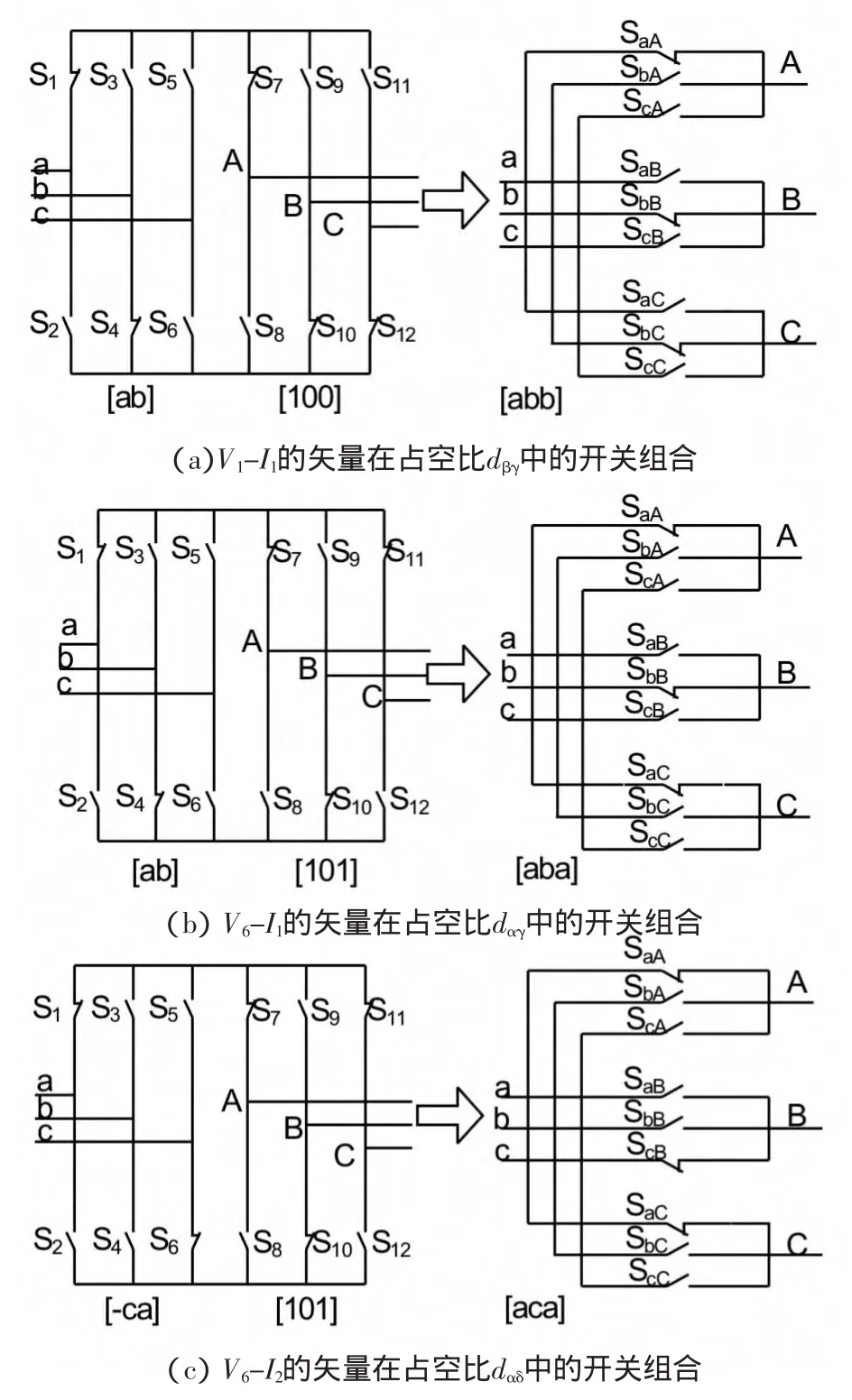
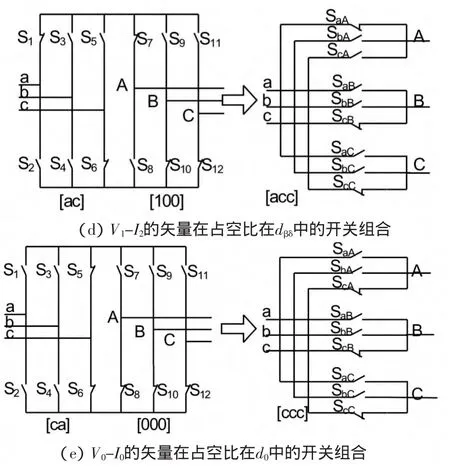
图6 不同矢量占空比中的开关组合

输入相电流在相同条件下，

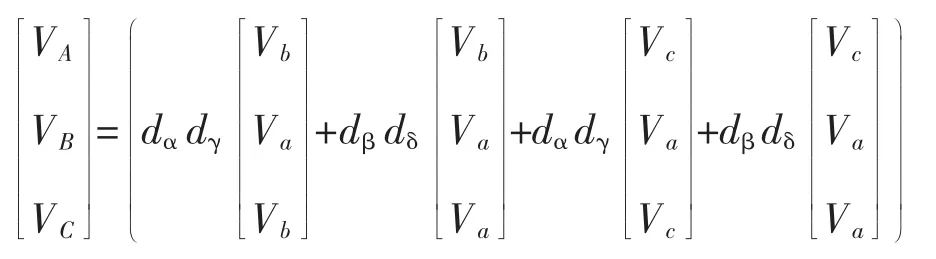
最后，零向量［ccc］对应为V0-I0的矢量对，以利用矩阵式变换器最小是开关数量来转换矩阵变换器如图6（d）所示。下一步是决定如何使4个矢量在开关间隔时间TS内和使用哪一个零向量［aaa］，［bbb］和［ccc］。在可能的开关组合顺序，一个标准的限制开关转换，每个矢量变化只有一次，通常是用来尽量减少总开关损耗。

间接空间矢量调制通常是用于矩阵式变换器输入电流和输出电压的分别控制。相互嵌套的双空间矢量PWM调制策略既可以保证输出线电压的良好正弦型，又可以保证输入相电流良好的正弦型，实现了在矩阵式变换器控制策略上运用空间矢量调制的目的，并且矩阵式变换器具有双PWM变换器的效果。采用这样的方法建模真实地反映了矩阵式变换器的交交变换控制过程。

5 结论

针对矩阵式变换器在理论和其拓扑结构上进行了深入的研究，进而对矩阵式变换器的控制策略进行了详细的分析和推导。

仿真时观察输入电压、电流和输出线电压、电流的波形，仿真模型的输入为220V/50Hz的三相对称电源；设定的输出频率为90Hz；矩阵式变换器的输入和输出波形如图7、图8所示。

图7 矩阵式变换器输出线电压

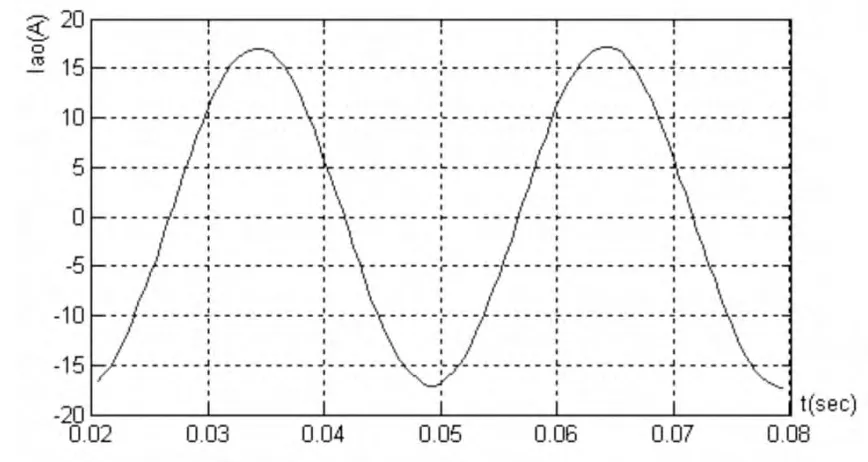
图8 输出电流的波形

可以看出，矩阵式变换器的输出线电压与一般的采用空间矢量调制策略的电压源PWM逆变器的输出线电压类似，矩阵式交-交变换器输入电压、电流正弦且基本同相，输出线电压正弦，脉宽调制、线电流正弦变化。验证了本文矩阵式模型和矩阵式变换器控制策略的正确性。

［1］韩竺秦，高锋阳，黄聪月.基于模糊控制器的异步转矩控制［J］.电气传动自动化，2009，31（5）：11-13.

［2］韩竺秦.矩阵变换器变速恒频风电系统应用［J］.变频器世界，2009，13（5）：79-82.

［3］孙 凯，周大宁.矩阵式变换器技术及应用［M］.北京：机械工业出版社，2008.

［4］汤宁平.矩阵变换器供电的交流励磁风力发电系统研究［D］.福州：福州大学，2005.

［5］吴胜华，钟炎平.高频链矩阵式正弦波变换器研究［J］.电力电子技术，2010，44（9）：11-13.

［6］Idris Z，Hamzah M K.Implementation of a New Single-Phase Cycloconverter Based on Single-Phase Matrix Converter Topology Using Sinusoidal Pulse Width Modulation with Passive Load Condition［C］.IEEE Conference on Industrial Electronics and Applications.Singapore：IEEE，2006：1-6.

［7］Patrick W-Wheeler，JoséRodríguez，Jon C.Clare.Matrix Converters：ATechnologyReview［J］.IEEE.Trans.Ind.Electron，2002，49（2）：276-287.