OMEGA/BEAM模拟医用加速器6 MV X-线的效率研究

戴振晖 王学涛 朱 琳 张 煜 刘小伟

1 (广东省中医院 广州 510120)

2 (南方医科大学 广州 510515)

3 (中山大学 广州 510275)

蒙特卡罗(Monte Carlo, MC)模拟是放射治疗剂量准确计算的常用方法[1,2]。对一个治疗射野的模拟，蒙特卡罗程序需追踪数十亿粒子的输运和能量沉积过程，非常耗时。因此，在不降低统计误差的情况下，如何缩短计算时间是一个非常值得研究的课题。OMEGA/BEAM 程序由加拿大国家研究院(National Research Council of Canada, NRC)开发，是专用于模拟医用直线加速器输出剂量的程序包，本文基于2011年5月18日发布的版本EGS nrc V42.3.2模拟 Varian 23EX加速器 6 MV X-线，研究BEAMnrc和DOSXYZnrc子程序的参数设置对蒙特卡罗计算效率的影响，计算机配置为：英特尔® 酷睿™ i7-3770 处理器，主频3.4 GHz，8 MB缓存。

1 材料与方法

1.1 相空间文件的计算

采用BEAMnrc模拟Varian 23EX医用直线加速器6 MV X-线，计算在源皮距为100 cm条件下10 cm×10 cm 射野的相空间文件，加速器治疗头主要部件包括靶、初级准直器、Be窗、均整器、电离室、射野镜、次级准直器及水体模等[3]。

BEAMnrc中主要参数设置为：AE=ECUT=0.70 MeV，光子的截止能量AP=PCUT=0.01 MeV，除钨靶外全局电子射程截断能量ESAVE=2.0 MeV(钨靶0.7 MeV)[4]，边界穿越算法选择 PRESTA-I，在EGSnrc中，若粒子能量低于预先设置的能量阈值，即没有足够的能量使它到最近的区域边界，则该粒子的活动就被终止，这样，将不产生能逃逸该区域的轫致辐射光子的可能性降到最低。本文主要研究三种方差减少技术，即均匀轫致辐射分裂(uniform bremsstrahlung splitting, UBS)、选择轫致辐射分裂(selective bremsstrahlung splitting, SBS)和方向轫致辐射分裂(directional bremsstrahlung splitting, DBS)；在BEAMnrc中，每一次轫致辐射事件产生NBRSPL个光子，每个光子的权重为 NBRSPL−1，不同方差减小技术可供选择的光子分裂数的范围不同[5]。在轫致辐射事件中，NBRSPL是基于入射电子的能量和方向，并正比于轫致辐射光子进入射野的几率。对于UBS，分裂数NBRSPL设置为一个固定值，每个轫致辐射事件产生NBRSPL个轫致辐射光子。对于SBS，NBRSPL是变化的，改变分裂数可最大化进入射野的光子分裂，最小化离开射野的无必要的光子分裂，SBS需设置背景分裂数，背景分裂数一般为分裂数的十分之一。若打开俄罗斯轮盘赌则UBS和 SBS将分裂更高权重的轫致辐射光子和来自湮灭事件光子，若关闭俄罗斯轮盘赌则不分裂更高权重的光子，进而减小跟踪消除权重粒子的CPU时间。DBS需设置分裂半径，且分裂半径要大于射野大小，打开电子分裂可提高相空间文件中电子通量计算的精确性。由于UBS的无方向特性导致很多CPU时间用于跟踪未进入感兴趣射野的分裂光子，另外，SBS也要求额外的CPU时间用于离开射野的轫致辐射光子的背景分裂。DBS则克服了UBS和SBS的缺点，确保射野内所有的光子有相同权重并消除背景分裂。表1为BEAMnrc中三种方差减小技术的参数设置[6,7]，选择轫致辐射需要输入背景光子分裂数，方向轫致辐射的电子分裂有ON和OFF两种状态。

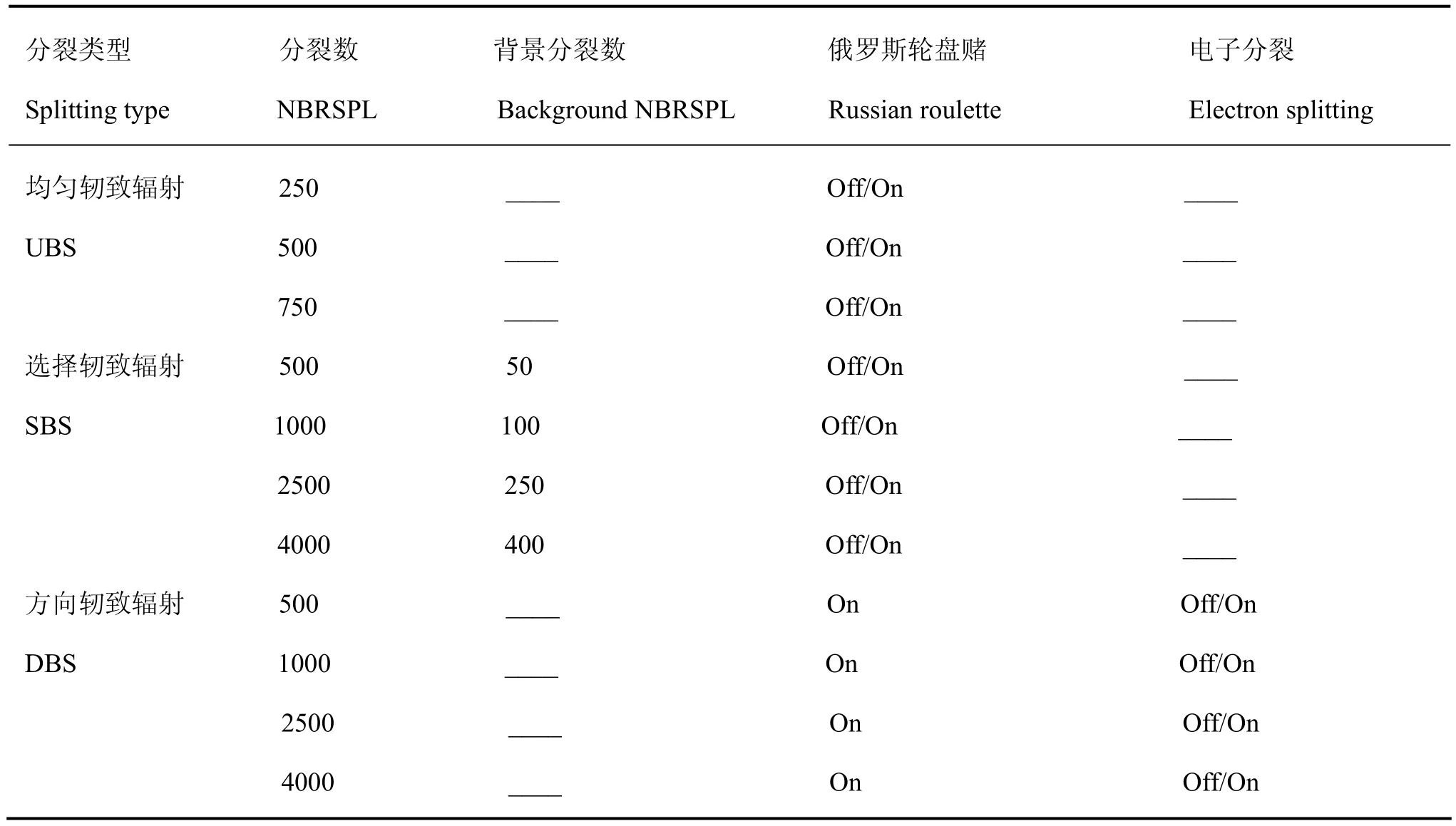
表1 BEAMnrc中三种方差减小技术参数设置表Table 1 Parameters of three variance reduction techniques in BEAMnrc.

1.2 水模体中剂量分布的计算

由 BEAMnrc生成的相空间文件作为DOSXYZnrc模拟的输入文件，计算水模体中的剂量分布。在DOSXYZnrc中可设置光子分裂数Ns和粒子循环数Nr，进入水模体的光子初始权重为W0，分裂 N次后每个光子的权重为 W0/N，这样就增加了进入水模体的目标粒子数。当使用光子分裂时关闭粒子循环，使用粒子循环时关闭光子分裂，分别设置分裂数和循环数进行剂量计算。

1.3 模拟效率

蒙特卡罗模拟的效率e定义为：e = 1/s2T，式中，s表示目标数据在数值上的不确定度，T表示CPU的计算时间。

Tp是 DOSXYZnrc模拟过程消耗 CPU的时间，Tj是BEAMnrc模拟过程消耗CPU的时间，平均不确定度为[5]：

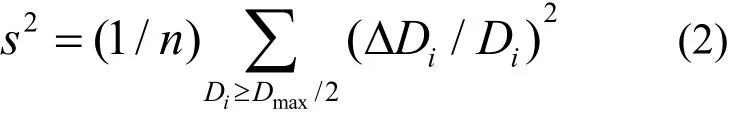
式中，Di表示第i个体素的剂量，DDi表示相关的统计不确定度， Di³ Dmax/2表示只有剂量大于最大剂量50%的体素才用于统计计算。

1.4 X-线射野剂量分布的测量和蒙特卡罗模拟

在BEAMnrc中设置电子的截止能量AE=ECUT=0.70 MeV，光子的截止能量AP=PCUT=0.01 MeV，电子射程截断能量ESAVE=2.0 MeV(钨靶0.7 MeV)，计算采用 DBS方差减少技术，轫致辐射粒子分裂数 NBRSPL=1000，分裂野半径 FS=30 cm，在DOSXYZnrc中设置Ns=40。

为验证优化计算模型的精确度，我们使用电离室进行了相同条件下的测量，并将计算结果与测量结果进行比较。在三维水模体中计算 Varian 23EX加速器6 MV X-线在SSD=100 cm、10 cm×10 cm射野的百分深度剂量和不同深度的离轴比曲线，水模体尺寸48 cm×48 cm×41 cm，体素尺寸0.5 cm×0.5 cm×0.5 cm。模拟的粒子数范围为5×108，以保证计算结果的统计误差均≤3%。在相同条件下，用Blue Phantom三维水箱(IBA公司，德国)测量百分深度剂量和离轴比曲线。图1为BEAMnrc和DOSXYZnrc之间的数据传输流程图。

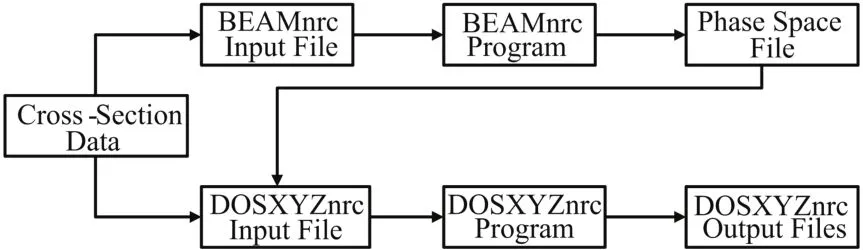
图1 BEAMnrc和DOSXYZnrc之间数据传输流程图Fig.1 Flow chart of data transmission between BEAMnrc and DOSXYZnrc.

2 结果

2.1 BEAMnrc的计算效率

BEAMnrc的计算效率如图2所示，以无轫致辐射分裂的计算效率为基准，由图可见，无电子分裂的DBS计算效率高于电子分裂的 DBS，当分裂数为 2500时，计算效率最高；使用俄罗斯轮盘赌的SBS计算效率高于不使用其的 SBS，当分裂数为2500时，计算效率最高；使用俄罗斯轮盘赌的UBS计算效率高于不使用其的UBS，当分裂数为750时，计算效率最高。三种轫致辐射的最高计算效率相比，DBS约为SBS的8倍、UBS 的17倍。轫致辐射分裂可大大降低不确定度，延长CPU计算时间，提高了计算效率。

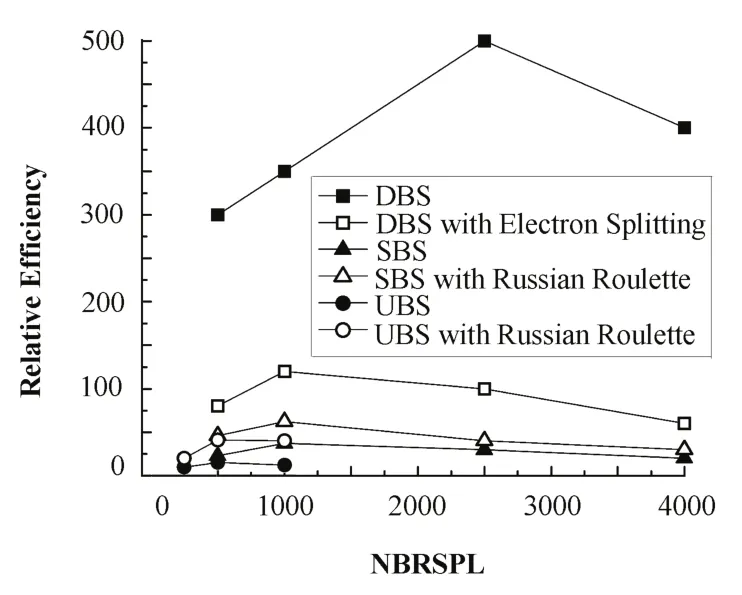
图2 不同分裂方式对应的相对计算效率Fig.2 Relative computing efficiency of different manner.

2.2 DOSXYZnrc的计算效率

DOSXYZnrc的计算效率如图3所示，以光子分裂数 Ns和粒子循环数 Nr为零时的计算效率为基准，当光子分裂数为40时计算效率最高。

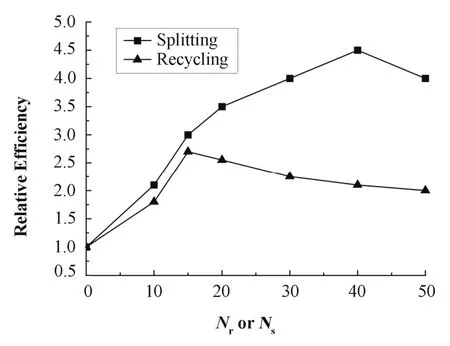
图3 光子分裂数和粒子循环数与相对剂量计算效率的关系图Fig.3 Relative efficiency of different splitting numberand cycling number.

2.3 使用与不使用最优参数的效率比较

表2为使用优化和未使用优化技巧的模拟效率对比，粒子数为 5×108。由表 2可见，当不使用优化技巧时计算时间是76 h，平均不确定度是3%，使用最优参数设置技巧的计算时间是13 h，平均不确定度是0.25%，计算效率是不使用优化技巧的490倍。

2.4 剂量分布测量和计算结果的比较

图 4(a)是 Varian 23EX加速器 6 MV X-线10 cm×10 cm射野的百分深度剂量分布图。由图可见，在剂量建成区域，蒙特卡罗模拟和测量值差异明显，估计与测量电离室本身的特性和侧向电子不平衡有关；在深度大于剂量最大点深度的区域，蒙特卡罗模拟和测量值无明显差异，误差小于 1%。图4(b)是6 MV X-线10 cm×10 cm射野不同深度的离轴比，按中心点剂量归一(为显示方便，深度为1.5、5、10、20 cm 的离轴比曲线分别乘以 1.00、0.85、0.65、0.35)。由图可见，在半影区域(10%–90%的剂量区域)，蒙特卡罗模拟和测量值差异明显，这是由于测量电离室本身的特性、测量条件等造成测量结果存在误差，在射野半影区计算剂量低是因为忽略了源电子束的宽度，未考虑源射束在射野半影区造成的多焦点影响；在剂量平坦区域，蒙特卡罗模拟和测量值未明显差异，大部分点的误差小于1.5%。

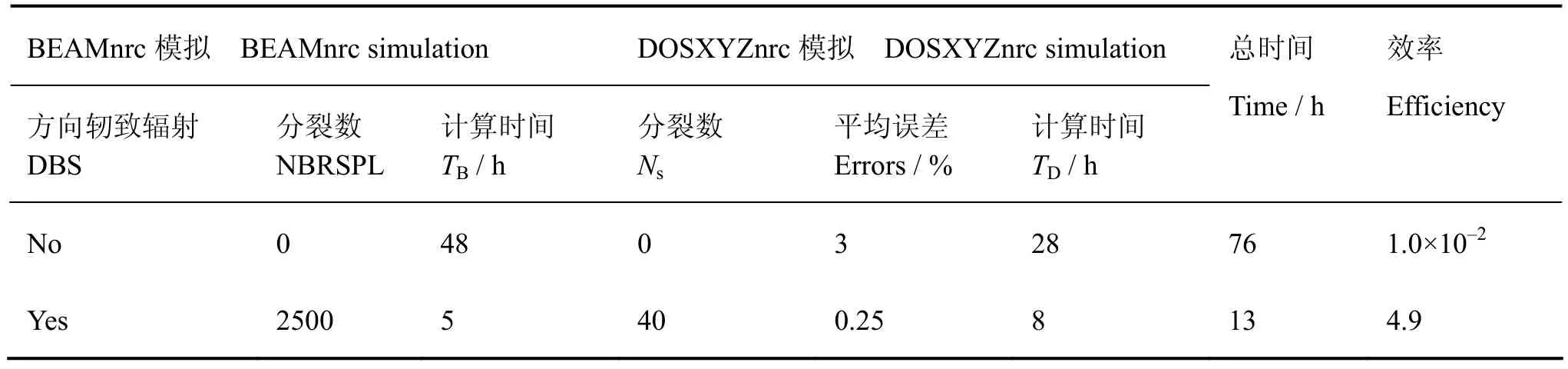
表2 使用优化和未使用优化技巧的模拟效率对比Table 2 Efficiency of the optimized method in beam and dose simulation relative to simulation without optimized method.

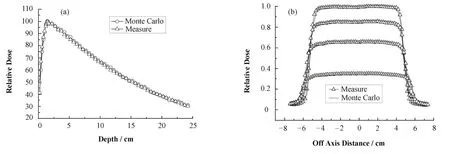
图4 10 cm×10 cm射野百分深度剂量和不同深度的离轴比蒙特卡罗模拟和测量值的比较Fig.4 Comparison of the MC and measured percent depth dose and off-axis ratio in different depths for 10 cm×10 cm field size.

3 讨论

对于 Varian 23EX加速器 6 MV X-线，在BEAMnrc中使用无电子分裂的DBS方式，分裂数为2500时计算效率最高；在DOSXYZnrc中，当光子分裂数为40，粒子循环数为15时，计算效率最高。其他因素(如射线能量、射野尺寸、体素尺寸、准直器铅门和多叶光栅的设置、EGSnrc的版本等)对计算效率的影响较小[8,9]。

EGSnrc是功能强大的软件程序包，是目前蒙特卡罗模拟医用加速器的主要程序[10]。VMC/XVMC/VMC++、MCDOSE/MCSIM、DPM 等[11–14]蒙特卡罗程序包使用各种工具提高运算速度，但带来较大误差；因此，用户可按照计算速度和统计误差的不同要求，选择不同的蒙特卡罗程序。

本文所述方法适用于一般的蒙特卡罗模拟程序，针对不同程序，要选择合适的改进效率的方法和参数，以提高计算效率。

1 Chetty I J, Curran B, Cygler J E, et al. The AAPM task group report No.105: issues associated with clinical implementation of Monte Carlo-based external beam treatment planning[J]. Medical Physics, 2007, 34(12):4818–4853

2 Reynaert N, Van der Marck S C, Schaart D R, et al.Monte Carlo treatment planning for photon and electron beams[J]. Radiation Physics and Chemistry, 2007, 76(4):643–686

3 王学涛, 陈少文, 戴振晖, 等. MatriXX 二维电离室阵列剂量分布的角度响应[J]. 核技术, 2012, 35(2):126–129 WANG Xuetao, CHEN Shaowen, DAI Zhenhui, et al.Angular dependence study on dose distribution of MatriXX 2-D chamber array[J]. Nuclear Techniques,2012, 35(2): 126–129

4 Ding G X, Duggan D M, Coffey C W, et al. First macro Monte Carlo based commercial dose calculation module for electron beam treatment planning—new issues for clinical consideration[J]. Physics in Medicine and Biology,2006, 51(11): 2781–2799

5 Popple R A, Weinberg R, Antolak J A, et al.Comprehensive evaluation of a commercial macro Monte Carlo electron dose calculation implementation using a standard verification data set[J]. Medical Physics, 2006,33(6): 1540–1551

6 Kawrakow I, Rogers D W O, Walters B R B. Large efficiency improvements in BEAMnrc using directional splitting[J]. Medical Physics, 2004, 31(10): 2883–2898

7 Sheikh-Bagheri D, Rogers D W O, Ross C K, et al.Comparison of measured and Monte Carlo calculated dose distributions from the NRC linac[J]. Medical Physics,2000, 27(10): 2256–2266

8 Kawrakow I, Walters B R B. Efficient photon beam dose calculations using DOSXYZnrc with BEAMnrc[J].Medical Physics, 2006, 33(8): 3046–3056

9 Kawrakow I, Mainegra-Hing E, Rogers D W O.EGSnrcMP, the new multi platform version of EGSnrc[J].Medical Physics, 2004, 31: 1731–1735

10 Rogers D W O, Faddegon B A, Ding G X, et al. BEAM:A Monte Carlo code to simulate radiotherapy treatment units[J]. Medical Physics, 1995, 22(5): 503–524

11 Kawrakow I, Fippel M. Investigation of variance reducetion techniques for Monte Carlo photon dose calculation using XVMC[J]. Physics in Medicine and Biology, 2000,45(8): 2163–2183

12 Neuenschwander H, Born J E. A macro Monte Carlo method for electron beam dose calculations[J]. Physics in Medicine and Biology, 1992, 37(1): 107–125

13 Ma C M, Li J, Pawlicki T, et al. MCSIM: A Monte Carlo dose verification tool for radiation therapy treatment planning and beam delivery[J]. Medical Physics, 2002,29(6): 1316–1320

14 张贵英, 曹磊, 邓君, 等. 15 MV医用电子直线加速器光核中子剂量分布的MC模拟及测量[J]. 核技术, 2010,33(1): 35–38 ZHANG Guiying, CAO Lei, DENG Jun, et al. Simulation and measurement of photon neutron dose distribution from a 15 MV X-ray medical electronic linear accelerator[J]. Nuclear Techniques, 2010, 33(1): 35–38