含双馈风电机组的系统阻尼优化研究

陈延云 戴申华 王 锐

（1.国电科学技术研究院，南京 210031；2.安徽省电力科学研究院，合肥 230601；3.陆军军官学院，合肥 230031）

随着风电装机容量在系统中所占比例的不断增大，风电对电力系统稳定性的影响日益显著[1]。与常规电力系统相比，含大容量风电场的电力系统对阻尼的要求更高[2]。附加阻尼控制具有调节效果好，经济可靠等优点，是常规发电机抑制系统低频振荡的有效手段之一。近年来，在风力发电机中配置附加阻尼控制器抑制系统低频振荡已成为业内所关注的重要问题。

双馈风力发电机由于能够运行在较宽的转速范围，具有投资小、控制灵活、可实现最大风能追踪等优点，应用越来越广泛，已成为新建风电场采用的主力机型[3]。双馈风力发电机主要通过变频器控制其注入系统的电磁功率，如果能够控制输出电磁功率与系统振荡频率相关，就可以在一定程度上削弱振荡幅度，减小系统振荡的时间，使系统快速恢复稳态运行。基于此，本文建立了应用于双馈风电机组的电力系统稳定器（PSS）模型，设计了相关参数，并在四机两区域系统中对附加阻尼控制效果进行了仿真验证。

1 双馈电机的矢量控制

双馈风力发电机是一个高阶的非线性强耦合的多变量系统，用传统的控制方法分析和求解这组非线性方程比较困难，系统无法获得较好的控制性能，而矢量变换控制技术可以简化电机内部各变量之间的耦合关系[4]。

在同步电机矢量控制中，通常采用的是以气隙合成磁链定向。但在交流励磁发电机中这种定向方法不太合适，因为在发电机定子绕组中存在漏抗压降的影响，若以气隙磁链定向，发电机的端电压矢量与控制参考轴之间会有一定的相位差，致使有功、无功电流分量的计算变得异常复杂。由于双馈风力发电机的定子通常是接在频率为工频的大电网上，在这个频率下定子绕组的电阻比其电抗小很多，可以忽略不计。此时，定子绕组总磁链与定子电压的矢量之间的相位正好相差90°。因此，在实际应用中，以定子电压矢量或者以定子绕组总磁链为参考矢量，可使交流电机得到可以与直流电机相媲美的控制性能。

根据定子磁链定向矢量控制策略，将同步旋转坐标系的d轴定向于定子磁链矢量sψ方向上，此时有

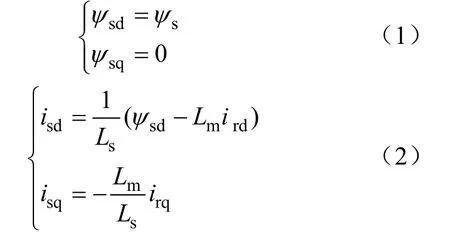
推导得到电磁转矩：

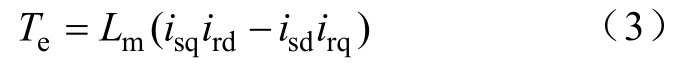
进而有总电磁功率：

将式（2）代入式（4）得

由式（5）可知，在定子磁链幅值恒定的情况下，双馈电机输出的电磁功率可由转子电流q轴分量irq独立控制，而转子电流和转子电压之间具有如下的关系：

由式（6）可知，转子电流的d、q轴分量可以由转子电压d、q轴分量分别控制。但是上述两式的第三项均为交叉耦合项，这些耦合干扰了转子电压对转子电流的控制作用，可以将其视为系统扰动。根据控制理论可知，闭环控制具有消除环内扰动的特点。因此，在双馈电机转子电流控制中，可以通过闭环控制以削弱上述扰动的影响，但是该扰动还是会在一定程度上降低电流闭环系统的静、动态特性，在这种情况下需要对扰动进行补偿。

引入扰动补偿量，令

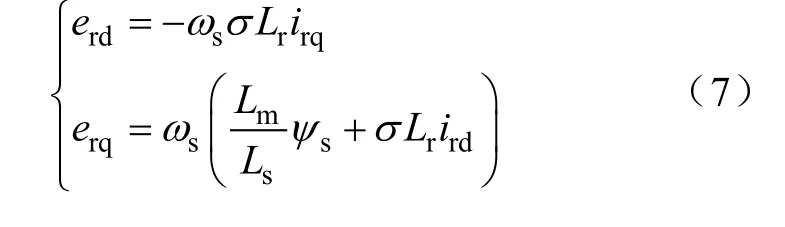
则有

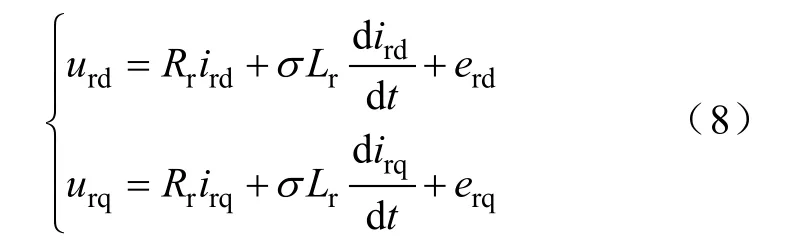
式（8）表明补偿扰动后，urd、urq实现了转子电流ird、irq的解耦控制，同时电压对电流的方程都是一阶惯性环节，可以得到很好的控制特性。

2 双馈风电机组的阻尼控制策略

由上述推导可知，通过调节转子电压q轴分量urq，进而可调节irq，最终实现对双馈风电机组注入系统电磁功率的调节。本文通过设计具有针对性的PSS模块，对转子电压q轴分量urq进行合理调节，控制转子电流q轴分量irq，从而使双馈电机输出与系统振荡相关的阻尼功率以阻尼低频振荡。

PSS的输入信号可以是任一受到系统振荡影响的双馈机组本地变量，如滑差信号、转速、定子功率等[5]。本文采用双馈电机的电磁功率作为输入信号，基本原理如图1所示。

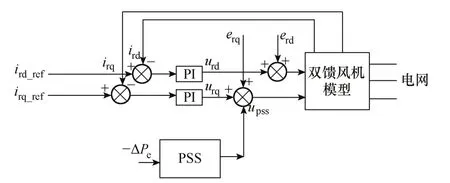
图1 双馈风电机组附加阻尼控制原理框图

PSS模块以电磁功率偏差量-ΔPe为输入信号，其输出量upss超前-ΔPe的角度设为θpss，如图2所示。

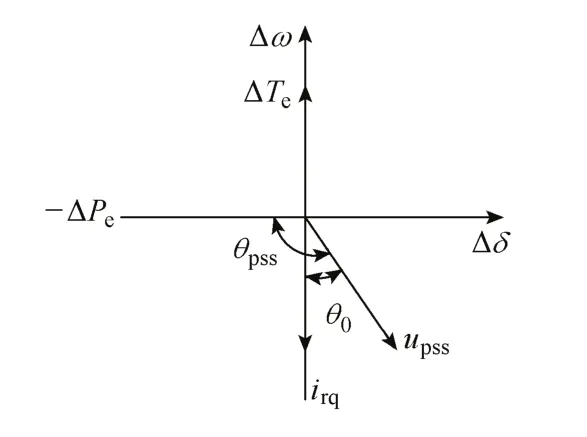
图2 PSS相位补偿原理

由于upss直接作用于urq并与urq同相位，根据式（8）第二式可以知道irq滞后upss一个角度θ0。由式（5）可知，ΔTe与irq相位相反，若要保证ΔTe和Δω同相，则须保证irq和Δω反相，因此PSS补偿的超前角度应该满足：

综上所述，利用附加PSS模块进行相位补偿，可以产生一个与Δω同相位的附加电磁转矩分量，对系统的低频振荡具有正阻尼作用。

3 附加控制器设计

3.1 PSS模型结构

文中采用的PSS模型如图3所示，由放大、隔直、相位补偿、限幅等环节组成。

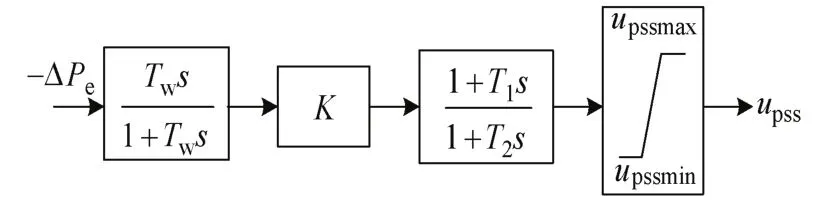
图3 PSS模型结构

隔直环节是一个微分环节，通常采用一个较大的时间常数Tw以阻断在电磁功率偏差量在稳态运行情况下的扰动信号，消除稳态运行中电磁功率变化对PSS输出的影响。

放大环节是一个比例环节，用于增强PSS的控制输出，但要合理选取PSS的放大倍数，以防止机电振荡、功率摆动和限制噪声等问题。

相位补偿环节由一级（或最多三级）的超前-滞后环节串联组成，提供一定的超前角度，补偿主要由系统控制环节引起的相位滞后，产生与Δω同相位的附加电磁转矩，进而改善系统阻尼。

限幅环节用于限制PSS的输出量对转子电压q轴分量的调节幅度，避免出现超调，防止在大扰动时PSS起不良作用。

3.2 参数整定

相位补偿环节参数的整定是参数整定过程的一个主要环节。根据式（9），如果知道irq滞后urq的角度θ0，那么就可以得到PSS的补偿角度θpss。所以，要设计出合理的补偿参数，就先要得到控制系统相关环节的相位滞后特性。

本文提出一种实用的相位滞后特性测试方法，采用测试信号法直接求取电磁转矩ΔTe相对于 PSS模块输出信号upss的滞后相位角[6-7]。具体步骤如下：

1）保持系统机械转矩恒定，在有功控制回路中的转子电压q轴分量urq节点处附加一系列很小的正弦扰动信号Δu，如图4所示。扰动信号表达式为

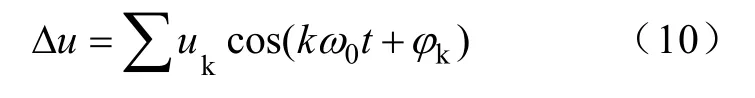
式中，uk和φk分别为小扰动的幅值和相位，kω0取值范围为

2）进行时域仿真，获得双馈电机的电磁转矩输出响应ΔTe。

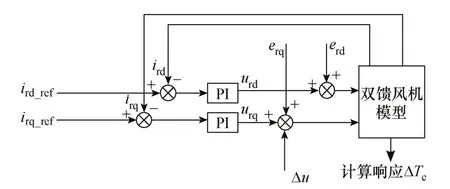
图4 测试信号法原理示意图

3）对ΔTe和Δu进行傅里叶分解，得到不同频率下ΔTe和Δu的相量。

5）根据相位补偿原理得到 PSS所需补偿的角度，便可确定补偿环节参数。

得到补偿环节参数后，再根据PSS的输入变量类型，确定隔直环节参数，并选取合适的增益参数和限幅值大小，便可得到一个配置好的PSS模块。

4 仿真研究

4.1 算例

在Matlab/Simulink中搭建四机两区域典型系统进行仿真分析，系统结构如图5所示。风电场通过变压器接入系统的节点 10，风电场出力 108MW，额定电压为575V。系统包括两个相似的区域，每个区域有两台耦合的机组，每台机组的额定容量均为900MVA，额定电压为20kV。

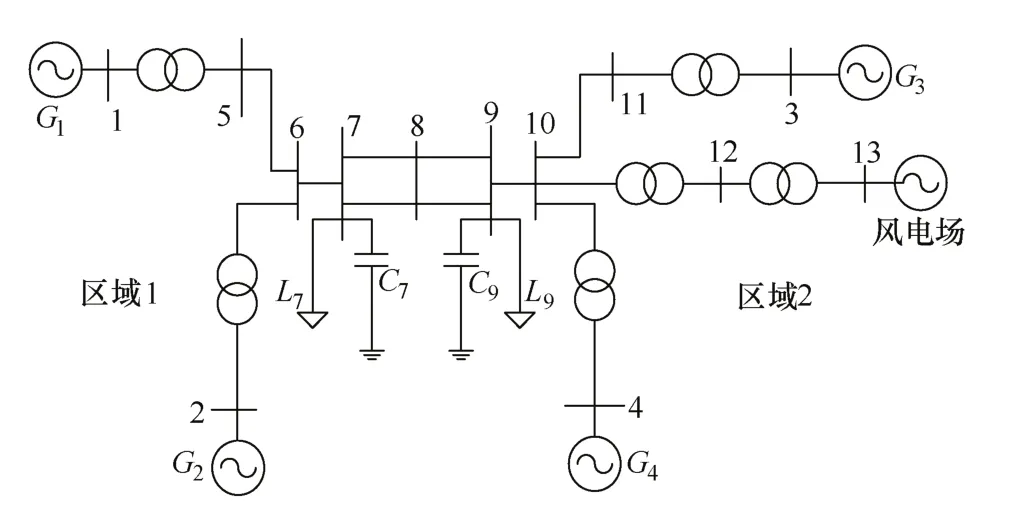
图5 含双馈风电机组的四机两区域系统

仿真过程：

1）给系统施加一定的小扰动，并对系统进行时域仿真，利用ESPRIT方法提取相关低频振荡模式[8]，结果如表1所示。

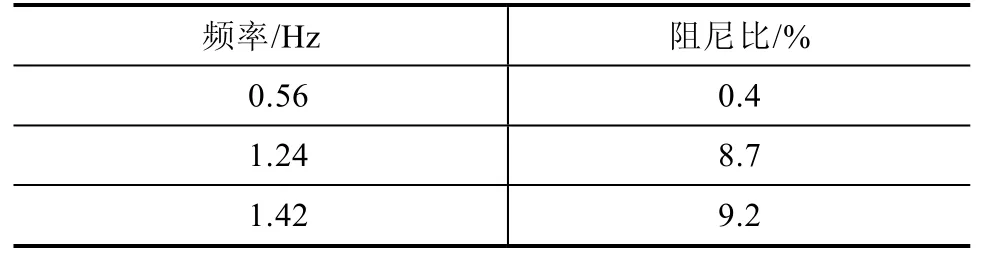
表1 系统低频振荡模式

接入风电场后该系统具有三个低频振荡模态，其中1.24Hz和1.42Hz这两个振荡模态阻尼比较大，而 0.56Hz的模态阻尼比很弱，因此仿真中的 PSS主要针对该模态进行设计。

2）利用测试信号法获取系统的相位滞后特性。相位滞后特性曲线如图6所示。

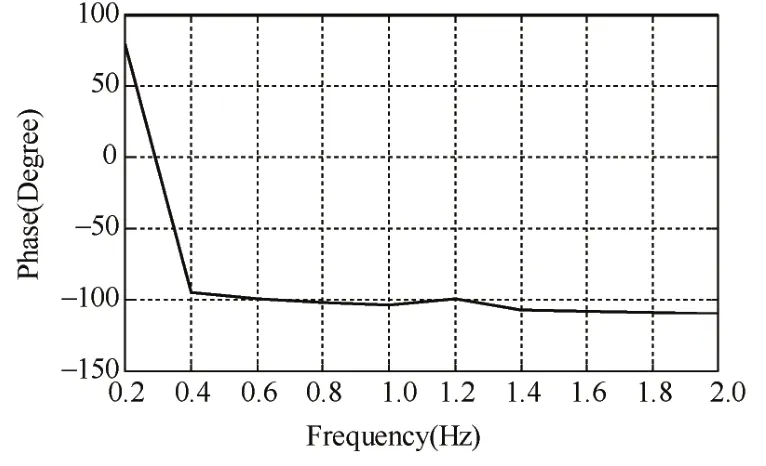
图6 系统相频特性曲线

3）根据相位补偿原理得到需要补偿的角度，计算得到表2中的PSS参数。

表2 PSS参数列表

4.2 仿真结果

在节点8和节点9之间施加三相接地短路故障，持续时间为 5个周波（0.1s）。通过对比双馈风电机组配置PSS前后系统中各发电机的电磁功率变化情况来分析系统阻尼的变化，文中重点分析与风电机组耦合紧密的区域2内的机组，结果如图7、图8所示。

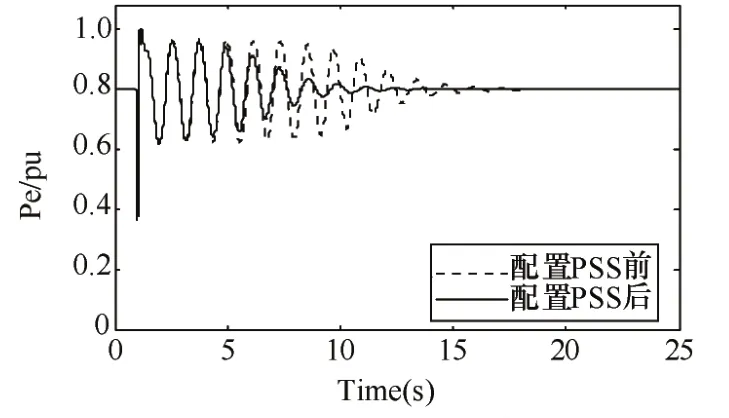
图7 发电机G3的电磁功率变化曲线

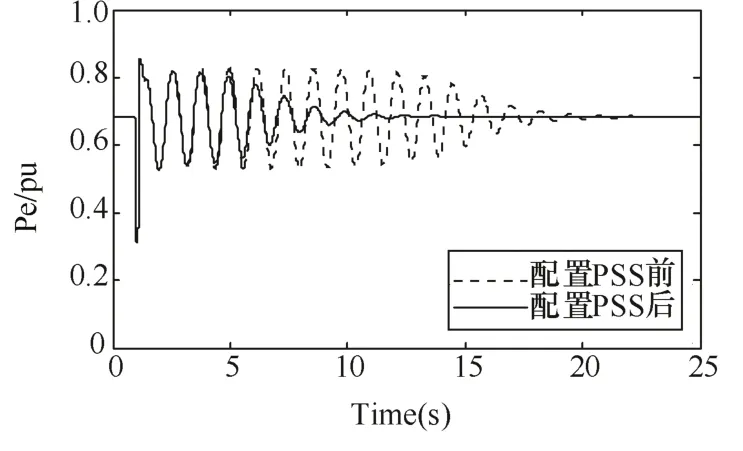
图8 发电机G4的电磁功率变化曲线

对仿真结果提取模态参数，配置PSS后0.56Hz模态的阻尼比由配置前的0.4%提高到了5.2%。

由仿真结果可以看出，双馈电机中配置PSS后提高了系统阻尼，对系统的低频振荡起到了一定的抑制作用，尤其是对与风电机组耦合较紧密的发电机组功率振荡具有较好的抑制效果。

5 结论

本文通过对双馈异步电机矢量控制机理的分析，提出了一种在双馈风电机组中配置PSS以提高系统阻尼、抑制低频振荡的方法，仿真结果表明附加PSS能够有效提高双馈风电机组改善系统阻尼的能力，对系统的低频振荡起到积极的抑制作用，该方法具有较强的实用性。下一步，将在此基础上开展对含风电场系统的阻尼协调优化研究。

[1]MARCUS V A, NUNES J A, HANS H Z, et al.Influence of the variable-speed wind generators in transient stability margin of the conventional generators integrated in electrical grids[J].IEEE Transactions on Energy Conversion, 2004, 19(4)： 692-701.

[2]郝正航, 余贻鑫, 等.改善电力系统阻尼特性的双馈风电机组控制策略[J].电力系统自动化, 2011,35(15)： 25-29.

[3]张子泳, 胡志坚.大型双馈风力发电系统小信号动态建模及附加阻尼控制器设计[J].电力系统保护与控制, 2011, 39(8)： 127-133.

[4]胡菲凡.变速恒频双馈风力发电机矢量控制研究[J].机电工程, 2009, 26(11)： 27-30.

[5]IEEE Recommended Practice for Excitation System Models for Power System Stability Studies.IEEE Std 421.5™-2005.

[6]方思立, 朱方.电力系统稳定器的原理及其应用[M].北京： 中国电力出版社, 1996.

[7]桂国亮, 郑国强.600MW 火电机组电力系统稳定器（PSS）试验及参数整定[J].安徽电力, 2008, 25(1)：1-4.

[8]聂永辉, 荣令玉, 张立艳.数学形态学和ESPRIT在低频振荡分析中的应用[J].电力系统及其自动化学报, 2012, 24(6)： 123-127.