基于变周期技术的自适应数据采集算法
牛保超,王志刚,王宪臻,郭琦,公衍宇
(河北工业大学 信息工程学院,天津 300400)
引 言
随着数字信息技术的飞速发展,针对各种传感器数据的实时采集和处理在现代工业控制和科学研究中成为必不可少的部分。因此,不同数据采集手段的有效实施已成为测控设备可靠性和安全性的重要保障。在实际应用中,一般采用固定周期的数据采集算法,根据预先设定的采集速率,周期性地采集性能数据。但是随着技术的日益成熟、应用领域的越加广泛,为了控制实时性和精确性,实时测控领域对数据采集的频率和精度需求越来越高。采样频率的升高导致系统负担加重,处理能力大幅降低,并且大量的数据对存储设备也提出了严峻的考验。因而,如何平衡数据数量、提高数据质量成了当前许多数据采集系统不得不面对的问题。
为了从根源上在保证数据质量的同时减少采集数量,本文提出了一种方案,依靠已经采集到的数据,实时地进行分析,从而不断地修正采样周期,使得采样周期能够快速、准确地适应被测对象的动态变化。以保证在不丢失有价值数据的同时,也不搜集过多价值不大的数据。
1 自适应数据采集算法
1.1 采集策略
在测控系统中,现实中的温度、压力、速度等模拟量通过各种类型的传感器按一定规律变换成为电信号,以满足信息传输、处理、存储和控制等要求,因而数据的采集方法显得尤为重要。图1是药物硬度检测实验过程中压力传感器随时间采集到的数据。
由图1可知,在0~25s的采集过程中,测得50个数据,数据量基本都在第5~13s内,仅用了16次即采集完毕,很明显,传统数据采集方法存在着严重的弊端:在采集对象变化平缓时采样次数过多,加大了系统压力;在采集对象变化剧烈时采样次数不足,不能准确反映采集对象的变化趋势。
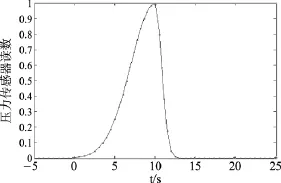
图1 药物硬度曲线
一般来说,有用信息往往来自数据的大幅度变化阶段,因为大幅度变化阶段往往是被测量发生质变的征兆。因而新算法需要实现的功能是,在有限的采样频率和存储容量下,更精确地记录变化情况,得到更多有用信息。具体来说,就是在数据变化平滑稳定时减少采集数据点数,而在数据变动剧烈时加大采集的数据点数。采集策略如下:
① 当采集到的系统数据变化平稳时,数据变化不明显,采用最大采集周期Tmax,减少对价值不大的数据的采集。
② 当采集到的系统数据变动剧烈时,数据急剧变化,采用最小采集周期Tmin,提高系统对变化数据的捕捉能力。
③ 当采集到的数据存在潜在信息量时,实时调整平衡关系,使得最优采样周期实时适应数据变化。
1.2 自适应算法设计
当前有多种针对采样周期调整采集数据的方法。如Bai等人在 NCS(Networked Control Systems)系统中,采用效用函数(utility function)建立系统性能与采样周期间的关系,并基于该函数调整采样周期,降低数据采集对系统性能的影响[1],但是没有考虑降低采样频率会增大采样失真度的问题。Choi等人采用随机抽样机制,并依据误差边界(Error Bound)自适应调整网络数据包的采样频率[2],但是存在降低采样频率会增大误差边界,进而增大采样失真度的问题。王亚沙等人采用一元线性回归对历史采样点拟合一条直线,然后根据该直线计算线性偏差平均值比,并根据线性偏差平均值比调整采样频率,以减小采样失真度[3],但是由于线性偏差平均值比只采用最近一次采样点相对于拟合直线的线性偏差与采样平均值作计算,存在误判率高、稳定性差的问题。盖炳帅等人也是采用一元线性回归对最近多个采样点拟合一条直线[4],但是根据该直线计算抖动比用提高或降低一定量采样周期的调整方式会存在采集变化速度可能跟不上系统信号的变化速度的弊端。
基于以上分析,本文在测控系统中提出了一种新的自适应的采集周期调整方法。该方法采用一元线性回归对最近的有限个采样点拟合一条直线,然后根据该直线的斜率大小,实时地调整采样频率。验证实验表明,该方法能够在降低平均采样频率的前提下减小采样失真度,且与同类方法相比失真度低,稳定性高。
自适应数据采集算法在采集策略实现的情况下要保证以下两点特性:
① 快速适应性。在采集数据的过程中,前后数据变化量必须迅速反映到采集周期上。
② 抗干扰性。能够剔除采集数据中因为瞬时、短暂的外界冲击而造成的变化。
假设y=f(t)[5]表示模拟量随时间变化的曲线,S={(t1,y1),(t2,y2),…,(tn,yn)}表示采样集合,其中t1<t2<t1<…<tn表示采样时间。测控系统通过采样到的各点的数据进行系统实时控制。用直线依次连接S中各点,得到采样曲线y′=f′(t),y′=f′(t)和y=f(t)间的面积表示采样失真度,则采样失真度为:
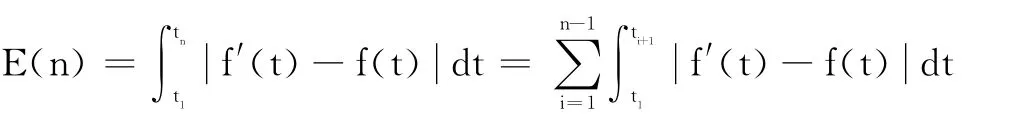
本采集方法利用对最近采样的N个点一元线性回归,拟合成一条直线。用yi+1表示下一个采样点的数值,yi,yi-1,yi-2,…,yi-N代表下次采样前最近的 N 个采样值,ti,ti-1,…,ti-N代 表 采 样 时 刻,并 且 满 足ti>ti-1> … >ti-N。以y=β0+β1t表示这N个点通过一元线性回归拟合成的直线。由一元线性回归可以求得β0和β1的最大自然估计:
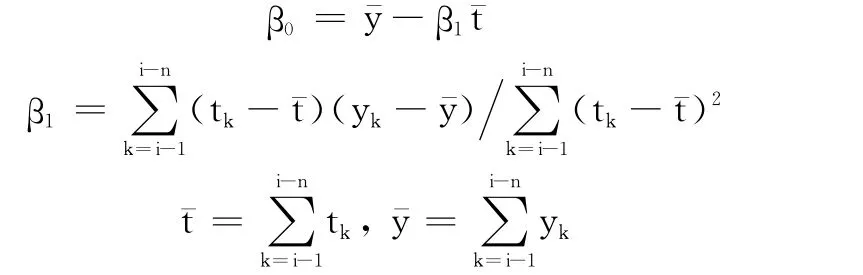

表1 斜率和采样间隔对应表
在实际数据采集中,经常发现有些数据会在一段平滑的抖动之间出现个别一两个数值的突变,而这种突变只是传感器受到外界不可避免的瞬时干扰而形成的噪声,不能代表被测量的变化趋势,在算法预测下一个采集间隔的过程中应当被剔除。所以在本算法中可以适当地加大一元线性回归的回归窗口,让多一些点参加拟合过程,可以很好地消除跳跃点的影响。因此,在数据采集之前,应该先确定参数N,来平衡干扰和灵敏度之间的取舍。
采集流程如图2所示。
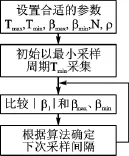
图2 数据采集流程图
2 仿真结果分析
针对本文图1中的实验数据,分别使用等间隔数据采集算法和自适应数据采集算法进行了仿真实验,仿真结果如图3所示。
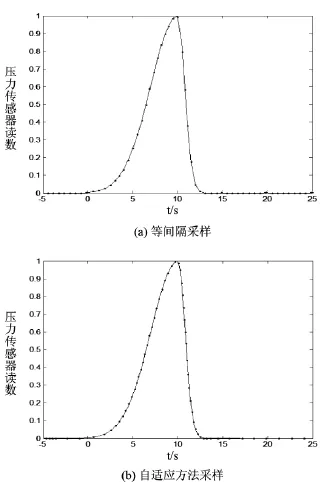
图3 两种算法的仿真结果
图3(a)和图3(b)都有60个采样点,不同的是图3(a)采用的是等间隔采样算法,采样间隔为0.1s,图3(b)采用的是自适应采样算法,其中使用的系统参数如表2所列。
通过对比可以很清楚地看到,在图3(a)中,所有的采样数据点都是均匀分布在时间轴上,而图3(b)中的采样点则是不均匀的。测量开始,以最小周期采样,采样4个点过后自适应算法启动。通过表3中两种算法仿真结果比较的数据,可以很明显地看到自适应采集的优势。
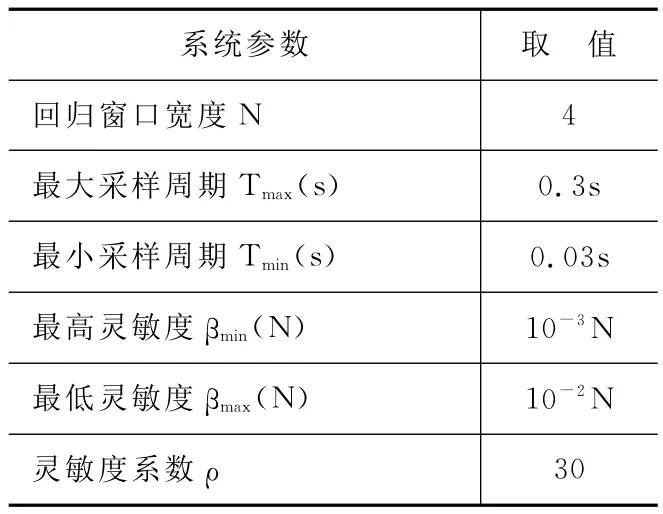
表2 自适应算法参数表
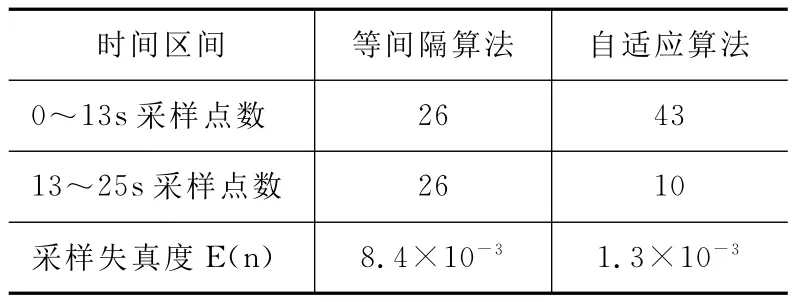
表3 两种算法仿真结果比较
结 语
传统的等间隔数据采集方法并不能按需采集数据,因此本文设计了一种自适应采集算法,在保证不丢失关键信息量的同时减少了采集数据的数量,提高了系统利用率。通过MATLAB仿真验证,自适应采集方法较传统的等间隔数据采集方法有一定的优势,是一种可行的代替方案。
本方案已经在药物硬度检测机上进行了测试,效果良好。
[1] Bai Jia,Eyisi E P,Xue Yuan,et al.Distributed Sampling Rate Adaptation for Networked Control Systems[C]//The First International Workshop on Cyber-Physical Networking Systems.Shanghai:ACM/IEEE,2011:768-773.
[2] Choi B Y,Park J,Zhang Zhi Li.Adaptive Packet Sampling for Accurate and Scalable Flow Measurement[C]//Global Telecommu-nications Conference.Dallas:IEEE,2004:1448-1452.
[3] 王亚沙,王光兴.网络性能管理中一种数据采集算法的研究[J].计算机研究与发展,2002,9(39):1031-1037.
[4] 盖炳帅,王劲林.网络管理系统中一种自适应的采样频率调整方法[J].网络新媒体技术,2012(1).
[5] Christos Stathis,Basil Maglaris.Modelling the self-similar behaviour of network traffic computer networks[J].Computer Networks,2000,34(1):37-47.

