模糊集对分析模型在大型电力变压器状态评价中的应用
俞乾 ,李卫国
(1. 华北电力大学 高电压与电磁兼容北京市重点实验室,北京 昌平,102206;2. 湖南省电力公司 永州电业局,湖南 永州,425000)
大型电力变压器状态评价是电力设备管理的一项重要内容,如何对大型变压器的运行状态进行科学、客观的评价是开展设备状态维修的前提[1-2]。目前,国内外学者对大型电力设备状态评价提出了多种方法,常用的评价方法可概括为单因子评价法和综合评价法两大类,其中综合评价法又包括主成分分析法、层次分析法、模糊数学法、人工神经网络法和灰色聚类法等。每种方法都有各自的优点与不足,许多学者针对各评价方法的不足进行了相应修正,并取得了一些成果[3-4]。然而,大型电力变压器是一个多元的复杂体系,影响变压器状态评价的诸多因素具有极强的不确定性和模糊性,评价因子与变压器状态等级间存在着复杂的非线性关系,使得至今仍然没有统一的设备状态评价模型。另外,各评价指标在实际观测过程中不可避免地存在误差,也对最终评价结果产生一定的影响。本文运用集对分析理论,借助确定性和不确定性分析方法对样本进行定性分析,然后,通过计算联系度对变压器状态进行定量评价,在评价指标权重的确定过程中,采用模糊层次分析法计算出各评价指标的权重值,对大型电力变压器的状态进行全面、客观评价。
1 基于模糊层次的集对分析模型
1.1 集对分析原理
集对分析理论是赵克勤于 1989年提出的一门新的处理不确定性问题的系统理论方 法[6],其核心思想是将系统内确定性与不确定性予以辩证分析与数学处理,体现系统、辨证、数学三大特点。该理论认为,不确定性是事物的本质属性,并将确定性与不确定性作为一个系统进行综合考察。集对分析将确定性分为“同一”与“对立”2个方面,将不确定性称为“差异”,从同、异、反3个方面分析事物及其系统。同、异、反三者相互联系、相互影响、相互制约,又在一定条件下相互转化[7]。通过引入联系度及其数学表达统一描述各种不确定性,从而将不确定性的辩证认识转化为数学运算。
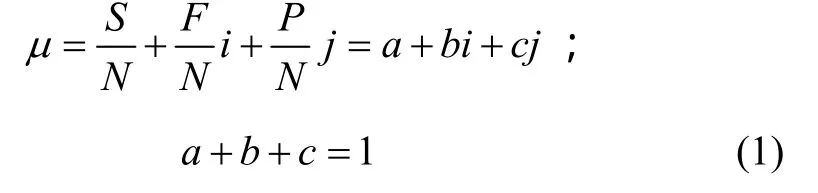
集对是指具有一定联系的 2个集合所构成的对子。集对分析理论的基本思路是[8]:在具体的问题背景下,对集合A和集合B组成的集对的特性进行分析,共得到N个特性,其中有S个为集对中2个集合所共有,这2个集合又在另外P个特性上相对立,在其余F个特性上关系不确定,一般地,F=N-S-P,则2个集合的联系度μ为式中:μ为联系度;S/N,F/N和P/N分别称为组成集对的2个集合在问题Q背景下的同一度、差异度和对立度。集对的同一度是指问题背景下趋同程度的刻画,用a表示,有a=S/N;F/N为差异度,简记为b;P/N为对立度,简记为c;i为差异标记,在[-1,1]区间视不同情况取值,i也可仅起标记作用;j为对立度系数,这里取为-1。j同样也可仅起标记作用。
从式(1)可以看出:联系度的表达式同时体现了同一、差异、对立三者的联系、影响与转化;当i=1时,差异度转化为同一度,当i=-1时,则差异度转化为对立度;当i在(-1,1)区间取值时,差异度中同一与对立各占一定比例。联系度μ与不确定系数i是该理论的基础,通过该理论可以描述随机、模糊、灰色等常见的不确定现象。
1.2 变压器状态评价的集对分析
变压器状态评价其实质是一个具有确定性的评价指标和评价标准与具有不确定性的状态参量及其变化相结合的分析过程。基于集对分析的变压器状态评价是将不同在役变压器的运行状况与既定变压器状态评价标准构成1个集对,通过两者间的比照分析,即可获得变压器状态评价的量化指标[9]。在进行状态评价时,假定有N个评价指标,其中S个评价指标优于标准,P个评价指标劣于标准,另有F个评价指标未测或缺乏比较,运用式(1)即可计算各评价样本的联系度μ,通过a,b和c三者的大小关系即可初步分析变压器的状态情况。由于不同变压器即使处于同一等级,也会因评价指标的差异而有所不同,因此,需对分级标准继续进行同一、差异和对立的集对分析。
我国GB/T 7252—2001(《变压器油中溶解气体分析和判断导则》)、Q/GDW 169—2008(《油浸式变压器(电抗器)状态评价导则》)等试验及运行规程对变压器的状态参量都规定有注意值。通过对各状态参量的特点进行分析,可将其分为两大类:一类是规定上限注意值的状态参量,另一类是规定下限注意值的状态参量。如GB/T 7252—2001规定:变压器色谱分析主要是对变压器本体、套管以及有载调压开关中的绝缘油中溶解气体进行分析,并根据产气速率、单一气体含量、总烃和三比值法判断变压器的运行状态。其中对产气速率的规定是:(1) 变压器总烃的绝对产气速率的注意值为 0.25 mL/d(开放式)或 0.50 mL/d(隔膜式);(2) 变压器总烃的相对产气速率不大于10%。其规定的注意值为上限注意值。又如绝缘电阻和吸收比,它们是反映电力变压器绝缘性能的关键参数,可以较灵敏地反映变压器的绝缘缺陷。通过测量变压器绝缘电阻和吸收比可以初步判断变压器绝缘性能,鉴别变压器绝缘的整体或局部是否受潮以及检查绝缘表面是否脏污、有无放电或击穿痕迹所形成的贯通性局部缺陷等。Q/GDW 169—2008规定:电力变压器的吸收比在 10~30 ℃时不低于 1.3。其规定的注意值为下限注意值。因此,根据变压器状态参量的特性,可将其分为越大越优型和越小越优型。对越大越优型状态参量,一般都存在规定的下限注意值,它表示状态参量检测值x较小时,设备的状态倾向于越差,发生故障的可能性就越大,因此,其联系度μ可以定义为:

当状态参量存在规定的上限注意值时,表示状态参量检测值x越大,发生故障的倾向性就越大,因此,对越小越优型指标,其联系度可定义为:

式中:S1,S2和 S3分别为评价指标的门限值;下标k表示第k项评价指标;下标x表示待评价的变压器s的第 k项评价指标(参量)的实测值;下标 s表示第 s台待评价的变压器。
1.3 基于模糊层次分析的权重系数确定
权重是各个指标在指标总体中的重要程度的度量,因此,权重确定是否科学、合理,直接影响着评价的准确性,是评价过程中的一个极其重要的环节。当前评价指标体系权重的确定大致可以分为2类: 一类是主观赋权法,另一类是客观赋权法。在实际应用中,可以根据实际情况采用适当的赋权方法来确定各指标的权数。在目前已有的变压器状态评价中,各项评价指标均取等权重,未能考虑到不同指标的相对重要性,会使最终的评价结果受到影响。本文将模糊层次分析法(fussy analytic hierarchy process,即FAHP)应用于各评价指标权重的计算。模糊层次分析法[13-14]是在层次分析法的基础上改进了比较判断矩阵的构成方式、一致性检验标准和比较判断矩阵的调整方法,使得层次分析法中较难进行的一致性检验和调整工作变得科学、准确和简便。运用FAHP分析电力变压器状态评价中各状态参量的权重可以分为5步:明确目标;建立递阶层次结构模型;利用专家综合评分法(0.1~0.9标度法)对某一指标下的各相关因素进行两两比较,构造模糊判断矩阵;检验模糊判断矩阵是否具有完全一致性;确定每层各影响因素的权重;获得各状态参量权重的层次总排序[12-14]。
1.3.1 变压器状态评价指标体系的建立
变压器的运行状态受多种因素的影响,它们从不同层次、不同侧面、不同程度上表征了变压器运行状况。变压器的状态信息数据复杂,十分庞大,结合国内变压器试验检修现状,可以将变压器状态评判的因素大致分为以下几类:变压器电气试验项目、绝缘油电气试验项目、油中溶解气体分析、运行工况、检修记录等。本文通过对变压器各项信息分析,依据状态评价指标体系的构建原则,建立具有3个层次的变压器状态评价指标体系,包括3个一级指标和12个二级指标,如图1所示。

图1 大型变压器评价指标体系框图Fig.1 Evaluation index system of large transformer
1.3.2 构建模糊判断矩阵
与层次分析法不同,元素间进行两两比较时,选取0.1~0.9共9个标度[10],如表1所示。若上层某准则为C,本层与之有关元素为a1,a2,…,an,用B=(bij)n×n来表示针对C,a1,a2,…,an之间的相对重要性程度。

表1 模糊判断矩阵标度含义Table 1 Meaning of fuzzy judgment matrix scale
1.3.3 模糊判断矩阵的一致性检验与调整
根据模糊一致判断矩阵的性质即任意指定行(列)和其余各行(列)对应元素之差为某一常数[11],对模糊判断矩阵进行一致性检验。只需检验矩阵B的任意2行(列)的对应元素之差是否为常数。若实际问题的复杂多变使得模糊判断矩阵的一致性难以满足现实问题的需要,则要借助模糊一致矩阵的充要条件及时地对模糊判断矩阵进行微调整,已达到期望的一致性。
1.3.4 权重的确定
设现有模糊矩阵R=(rij)n×n,则各元素的权重为[11]:

式(4)中,若R为模糊互补矩阵,则参数a必然满足[11]:

式中:a与任意两元素的权重之差成反比例关系,若a越小,则两元素的权重之差就越大,且两元素间的权重之差在 a=0.5(n-1)时达到最大;反之,两元素间的权重之差就越小。事实上,a反映了决策者对待元素间重要程度差异的重视,常取a=0.5(n-1)[14]。在模糊一致矩阵达到一致性要求后,利用式(4)和(5),可分别得到各层评价指标权重,如表2所示。

表2 评价模型中个评价指标权重Table 2 Evaluation index weight in evaluation model
2 评价指标等级的划分和联系度的计算
2.1 评价指标状态等级标准的划分
根据现有的变压器绝缘状态划分标准、《电气设备预防性试验规程》《油浸式变压器(电抗器)状态评价导则》和《变压器油中溶解气体分析和判断导则》,借鉴国内外学者的相关研究成果和历史资料,分别给出上述实验项目参量的状态等级评价标准,见表3~5。

表3 预防性试验指标状态等级评价标准Table 3 Index state evaluation grades of preventive test

表4 绝缘油试验指标状态等级评价标准Table 4 Index state evaluation grades of insulation oil test

表5 油中溶解气体试验指标状态等级评价标准(质量分数)Table 5 Index state evaluation grades of dissolved gas in oil test ×10-6
2.2 联系度表达式的确定
设 A={ai|i=1,2,…,n}为变压器某方面(如电气试验项目参数)待评价指标的集合,B1,B2,B3和 B4分别为评价指标所对应的各分级(良好、较好、一般、注意)评价标准。要从某一方面确定变压器运行状态的等级,需先确定各实际监测指标与其所对应的各级评价标准之间的联系度 μ(A,B1),μ(A,B2),μ(A,B3)和μ(A,B4)。评价指标与哪级的评价标准间联系度越大,表明评价指标越接近哪一级,此时,认为评价指标隶属于这一级。
现以确定评价指标与良好状态的评价标准间的联系度μ(A,B1)为例,确立联系度表达式。设待评价指标集A共有N个参数,其中处于良好状态的指标有S个,与其相对应的各指标权重为 u1,u2,…,uS;处于较好状态的指标有F个,与其相对应的各指标权重为t1,t2,…,tF;处于一般和注意状态的指标个数为P个,与其相对应的各指标权重为v1,v2,…,vP。采取以下标准来判别同异反联系度:(1) 视为同一的标准是评价指标实测值在探讨级别标准内取值;(2) 视为对立的标准是评价指标实测值在与探讨级别相隔的级别标准内取值;(3) 视为差异的标准是评价指标的实测值在与探讨级别相邻的级别标准内取值[17]。按此标准,综合考虑各评价指标的特性权重后,μ(A,B1)联系度表达式为

式中:ik表示待评价指标集合A中权重为tk的指标其实测值与良好级别中对应的该指标的标准值之间的模糊联系度。按照相同的方法,可以建立待评价指标集合与较好、一般、注意状态的指标标准集合间的联系度。
3 实例分析
某变压器型号为SFSZ9-31500/110,32 ℃时测得直流电阻不平衡系数为1.19%,绝缘电阻为R60=1100 MΩ,R15=780 MΩ,泄漏电流为34 µA,吸收比为1.41,主变本体介损为0.341%。绝缘油试验结果见表6。

表6 运行中绝缘油试验油气体组分(质量分数)Table 6 Content of insulating oil in operating 10-6
由于表3中给出的绝缘电阻和主变本体介损的状态等级评价标准都是环境温度为20 °C时的值,故需要将以上数据进行转换:对绝缘电阻,可以依据式R2= R1× 1.5(t1-t2)/10来转换(其中,R1和R2分别为对应温度 t1和 t2时的绝缘电阻);对于介损,可以依据式tan δ2= tan δ1× 1.3(t2-t1)10换算(其中,tan δ1和 tan δ2分别为温度t1和t2时的介损值)。转换后,在20 ℃时,绝缘电阻为1 789.5 MΩ,介损为0.467 2%。
然后,按照本文的同异反判断标准,使用模糊集对分析对该变压器状态进行评价,可得电气试验项目待评价指标集、绝缘油试验项目待评价指标以及溶解气体分析项目评价指标与设备状态评价标准间的联系度,如表7所示。

表7 评价指标集和标准集间的联系度Table 7 Affiliation degree between evaluation index and standard set
评价指标与哪级的评价标准间联系度越大,表明评价指标越接近哪一级。从表7所示的评价结果看:从电气预防性试验指标的联系度来判断,变压器的运行状态为一般,这与文献[5]中模糊评判法的评价结果一致;从绝缘油试验指数的联系度来判断,变压器的运行状态为一般,与文献[5]中的评价结果一致;从油中溶解气体指标的联系度来判断变压器的运行状态较好,而文献[5]中模糊评判法的评价结果为良好。
4 结论
(1) 提出了基于集对分析的联系度评价模型。针对变压器状态信息的模糊性和不确定性,采取模糊联系度从同一度、差异度、对立度3个方面刻画了不确定信息,实现对实验数据中隐含信息的充分挖掘,确保了信息的完整性。
(2) 采取模糊层次分析法实现了权重在各评价指标间的合理分配,客观、真实地反映了各参量在状态评价中的作用。
(3) 运用提出的方法实现了运行中的变压器的状态进行评价。该方法思路清晰,实现过程简捷,评价结果全面、准确,适于在设备状态评价领域进行推广。
[1] 吴立增. 变压器状态评估方法的研究[D]. 河北: 华北电力大学电气工程学院, 2005: 1-9.WU Lizeng. Assessing approach of transformer condition[D].Hebei: North China Electric Power University. School of Electrical Engineering, 2005: 1-9.
[2] 马辉. 实现变压器状态检修的方法[J]. 高电压技术, 2001,27(7): 70-84.MA Hui. Condition maintenance method of transformer[J]. High Voltage Engineering, 2001, 27(7): 70-84.
[3] 张镱议, 廖瑞金, 杨丽君, 等. 基于云理论的电力变压器绝缘状态评估方法[J]. 电工技术学报, 2012, 27(5): 13-20.ZHANG Yiyi, LIAO Ruijin, YANG Lijun, et al. An assessment method for insulation condition of power transformer based upon cloud model[J]. Transactions of China Electrotechnical Society,2012, 27(5): 13-20.
[4] 郑蕊蕊, 赵继印, 吴宝春, 等. 基于加权灰靶理论的电力变压器绝缘状态分级评估方法[J]. 电工技术学报, 2008, 23(8):60-66.ZHENG Ruirui, ZHAO Jiyin, WU Baochun, et al. Method for isolative condition classification evaluation of power transformers based on weight coefficient grey target theory[J].Transactions of China Electro Technical Society, 2008, 23(8):60-66.
[5] 王谦. 基于模糊理论的电力变压器运行状态综合评估方法研究[D]. 重庆: 重庆大学电气工程学院, 2005: 20-56.WANG Qian. Study of the comprehensive assessment method for the power transformer condition in service with fuzzy theory[D]. Chongqing: Chongqing University. College of Electrical Engineering, 2005: 20-56.
[6] 赵克勤. 集对分析及其初步应用[M]. 杭州: 浙江科学技术出版社, 2000: 57-83.ZHAO Keqin. Set pair analysis and its preliminary application[M]. Hangzhou: Zhejiang Science and Technology Press, 2000: 57-83.
[7] 赵克勤, 宣爱理. 集对论: 一种新的不确定性理论方法与应用[J]. 系统工程, 1996, 14(1): 18-23.ZHAO Keqin, XUAN Aili. Set pair theory: A new theory method of non-define and its applications[J]. Systems Engineering,1996,14(1): 18-23.
[8] 赵克勤. 基于集对分析的方案评价决策矩阵与应用[J].系统工程, 1994, 12(4): 67-72.ZHAO Keqin. An application of the scheme-appraisal decision matrix based on set pair analysis[J]. Systems Engineering, 1994,12(4): 67-72.
[9] 廖瑞金, 郑含博, 杨丽君, 等. 基于集对分析方法的电力变压器绝缘状态评估策略[J]. 电力系统自动化, 2010, 34(21):55-60.LIAO Ruijin, ZHENG Hanbo, YANG Lijun, et al. A power transformer insulation condition assessment method based on set pair analysis[J]. Automation of Electric Power Systems, 2010,34(21): 55-60.
[10] 张学镭, 周兰欣, 陈海平, 等. 基于模糊层次分析法的直接空冷凝汽器防冻性能监测[J]. 动力工程学报, 2012, 32(10):809-814.ZHANG Xuelei, ZHOU Lanxin, CHEN Haiping, et al.Antifreezing performance monitoring of direct air-cooled condenser based on fuzzy analytic hierarchy process[J]. Journal of Chinese Society of Power Engineering, 2012, 32(10):809-814.
[11] 李永锋, 朱丽萍. 基于模糊层次分析法的产品可用性评价方法[J]. 机械工程学报, 2012, 48(14): 183-191.LI Yongfeng, ZHU Liping. Product usability evaluation method based on fuzzy analytic hierarchy process[J]. Journal of Mechanical Engineering, 2012, 48(14): 183-191.
[12] ZENG Xuelan, GONG Yande, CHENG Xianjuan. Improvement of priority method for fuzzy complementary judgment matrix[C]//2005 IEEE International Conference on Granular Computing. Beijing, 2005: 704-707.
[13] Yang J B, Singh M G. An evidential reasoning approach for multiple attribute decision making with uncertainty[J]. IEEE Trans Syst, Man, Cybern, 1994, 35(24): 1-18.
[14] 万星, 丁晶, 张晓丽, 等. 区域地下水资源承载力综合评价的集对分析方法[J]. 城市环境与城市生态, 2006, 19(2): 8-10.WAN Xing, DING Jing, ZHANG Xiao-li, et al. Set pair analysis for comprehensive evaluation on regional groundwater resources carrying capacity[J]. Urban Environment & Urban Ecology,2006, 19(2): 8-10.

