盘式异步磁力联轴器三维气隙磁场计算及试验研究

杨超君， 管春松， 徐燕飞， 胡友

(江苏大学机械工程学院，江苏镇江 212013)

0 引言

目前电机在变频器供电时，电机的定子电流中含有大量的时间谐波，使电机气隙磁场受到影响，严重时可能导致电机振动和噪声的增大［1］。另外变频器在低电压场合下可能无法工作;在低速工况下可能降低散热风扇的效率，造成电机过热［2－3］。近年来随着永磁驱动技术的发展，根据电磁感应原理，已成功研制出了一种盘式异步磁力联轴器，被用于连接电机与负载之间，通过调节联轴器的气隙磁场就可实现对电机输出转矩和输出转速的控制，不但具备变频器在线调速、节能、起制动性能等，而且不会导致电机的振动和噪声，不受低电压、低转速及安装不对中等场合的限制。因而在钢铁冶金、发电热电、造纸和纸浆、矿山和煤炭开采行业具有很好的应用前景［4－6］。

盘式异步磁力联轴器可实现动力的非接触传递，通过对气隙大小的调节，从而实现不同转矩和速度的输出。为保证联轴器传递性能的平稳性，减小输出转矩脉动，应尽量使静态气隙磁场波形保持较好的正弦性［7］。另外分析静态气隙磁场可达到验证磁路的目的，有利于联轴器的结构改进。在气隙磁场的求解方法中，最常见的方法有解析法和有限元数值法，由于有限元数值法具有前处理复杂且计算时间长等特点［8］，本文选用解析法对气隙磁场进行求解。常用的解析法有等效磁势法［9］、等效电荷法［10］及等效面电流法［11］，由于等效电流法适用于任意形状均匀磁化的永磁体，故此处采用等效面电流法研究气隙磁场的分布规律。本文采用等效面电流法建立盘式异步磁力联轴器气隙磁场的三维数学模型，推导出气隙中任意场点的磁密公式。以一台18极的盘式异步磁力联轴器样机为例，计算得出气隙磁场的空间分布图，并通过试验对气隙磁场进行测量，将测量结果与解析结果进行比较。

1 分析模型

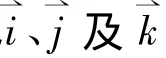
图1 联轴器三维理论模型Fig．1 3D theoretical model of axial asynchronous permanent magnet coupling

本模型中其他参数的具体含义如下:l1为永磁体的轴向宽度;l2为气隙长度;l3为导体转子盘的槽深;l为永磁体盘的底部到导体转子盘底部的轴向距离;R1为永磁体盘的外表面半径，同时也是导体转子盘的外径;R2为永磁体盘的内表面半径，同时也是导体转子盘的内径;N为永磁体的磁极数。

2 三维气隙磁场的解析表达式

2.1 基本假设

1)本模型只考虑永磁体在气隙处产生的静态磁场，不考虑速度效应，即气隙磁场计算时，忽略了由铜导体内部的涡流在气隙处产生的附加磁场;

2)由于气隙长度与磁力联轴器的轴向尺寸相比较小，可以近似认为气隙处某一位置的磁场沿轴向几乎没有变化，故可用气隙平均厚度处的磁场来等效气隙磁场［12］;

3)永磁体材料为钕铁硼，且沿轴向均匀磁化。钕铁硼材料的退磁曲线可以近似为直线，回复线与退磁曲线重合，不考虑永磁体退磁效应;

4)不考虑永磁体转子盘上轭铁产生感应磁场的影响;同时不考虑联轴器模型的漏磁，在联轴器模型以外部分磁感应强度为零。

2.2 气隙中任意场点的磁感应强度计算公式

由基本假设可知，理论计算的模型是不考虑速度效应的，即只考虑气隙中的静态磁场，因此气隙磁场只由永磁体提供。由于联轴器的奇数号磁极和偶数号磁极表面产生的等效面电流不相同，故而各个等效面电流在气隙中产生的磁感应强度表达式也不一致。因而，此处将永磁体的扇形块进行编号，分为奇数号和偶数号，首先分别求出奇数号磁极、偶数号磁极的各个等效面电流在P点处的磁感应强度(m)及(m)，m=1，2，3，4，最后将所求结果进行矢量叠加即可得到整个永磁体模型在P点处的磁感应强度值。由于计算方法的类似性，下面仅以3号扇形永磁块的外表面(面ABCD)为例，对其表面的等效面电流在气隙中任意场点P的磁感应强度计算公式推导如下。

如图1所示，面ABCD上任意源点Q到气隙中任意场点P的矢径表达式为

面ABCD上的外法线单位向量为

剩余磁化强度为［13］

式中:Bs为永磁体的剩余磁感应强度;μ0为真空磁导率。

一般来说，企业管理信息化指的是充分运用信息技术手段，从而对企业实施信息化管理。企业在开展信息化管理的过程中，一般会涉及诸多环节，并充分运用现代化信息技术，构建一个高效、完善的信息网络系统，整合以及集成企业的信息流、物流、工作流以及资金流，不断提升企业管理的水平以及效率，并优化配置企业的各类资源，从而提升企业的市场竞争力，实现最大化的经济利益。企业信息化管理主要覆盖了三个不同的方面。通常，上述企业信息化管理的三个方面之间存在着非常紧密的联系，相互制约却又相互融合。在企业战略管理当中，企业管理信息化是一个十分重要的环节，有助于企业取得更好的未来发展。

则面ABCD上的等效面电流密度为

式中μr为相对磁导率。

将式(1)与式(4)代入毕萨定律中，可得到面ABCD上的等效面电流在P点产生的磁感应强度表达式为

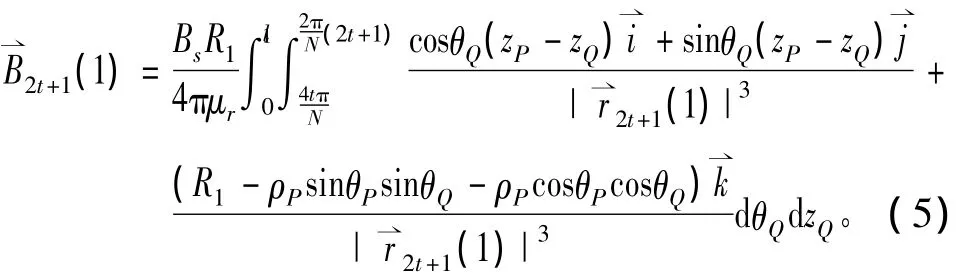
同理，可分别得到奇数号永磁块及偶数号永磁块的所有表面上的等效面电流在P点处的磁感应强度，进行矢量叠加后可得到整个永磁体在P点处的总磁感应强度为

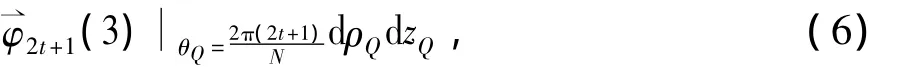
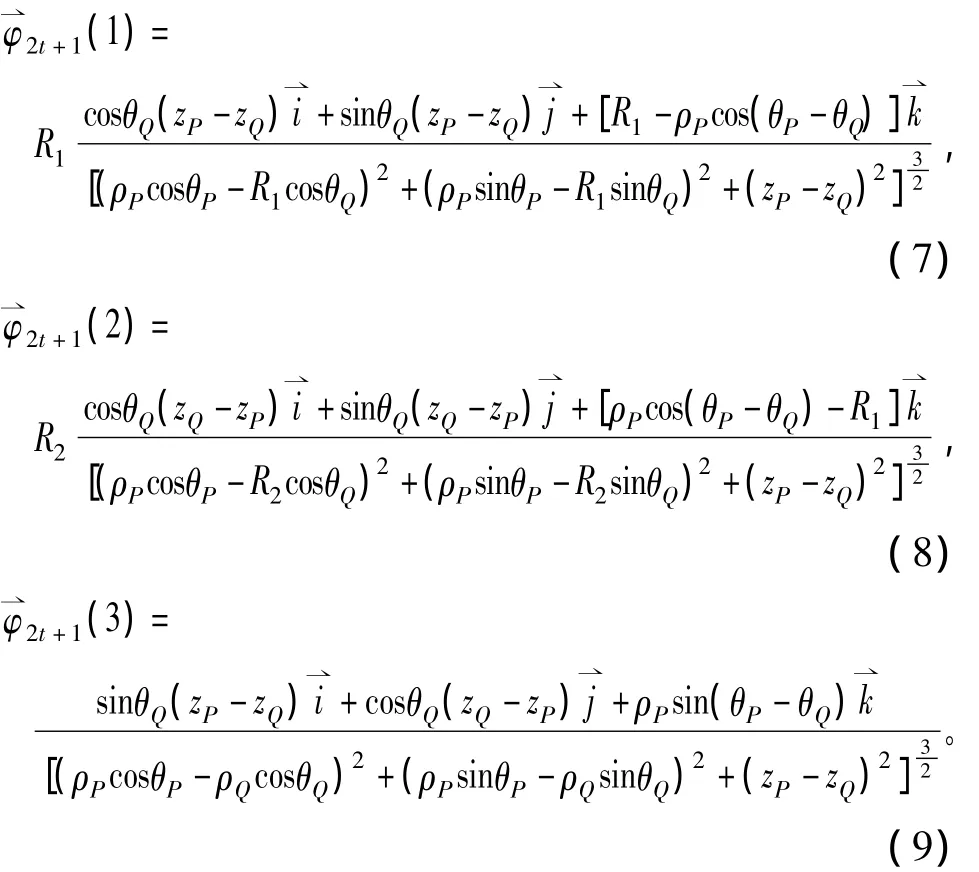
通过对式(6)的计算后可以得出磁感应强度沿x向、y向、z向的分向磁感应强度，然后通过笛卡尔坐标系与柱坐标系之间的关系进行转换，可求出磁感应强度的径向分量Br、周向分量Bθ和轴向分量Bz数值，更为方便的研究气隙磁场的变化规律。

3 计算实例

结合联轴器的实际模型，给出如下的具体结构和性能参数:磁极数N=18;外径R1;内径R2;永磁体轴向厚度l1=0.01 m;剩余磁感应强度Bs=1.2T;相对磁导率μr=1.05;气隙厚度l2=0.006 m;真空磁导率μ0=4π ×10－7N/A2;铜转子轴向厚度l3=0.015 m。

3.1 轴向磁感应强度Bz的变化曲面图

如图2所示，轴向磁感应强度Bz的幅值在－0．7T到0．7T之间呈现周期性变化。在固定半径的圆周上以一对N、S磁极周期性交替变化，因此出现9个波峰和9个波谷，形状如“近似正弦波”，可实现联轴器转矩的稳定输出。并且Bz的大小关于平均半径R=(R1+R2)/2圆周对称，由R=R1和R=R2向平均半径圆周处略有递减，在平均半径圆周附近达到最小值。

图2 轴向磁场三维空间分布Fig．2 Three-dimensional spatial distribution of the axial magnetic field

3.2 径向磁感应强度Br的变化曲面图

如图3所示，径向磁感应强度Br在气隙平均厚度平面上的三维空间分布呈现周期性的分布，其幅值大小在－0.3～0.3T之间变化。由图3(b)可知，一个周期内，径向磁场磁感应强度Br的空间分布形状如“马鞍形”，从内径向外径处看，形成两端高中间低的分布形状，径向磁感应强度也形成先减后增的变化趋势，并在平均半径R=(R1+R2)/2上磁感应强度值达到最小。

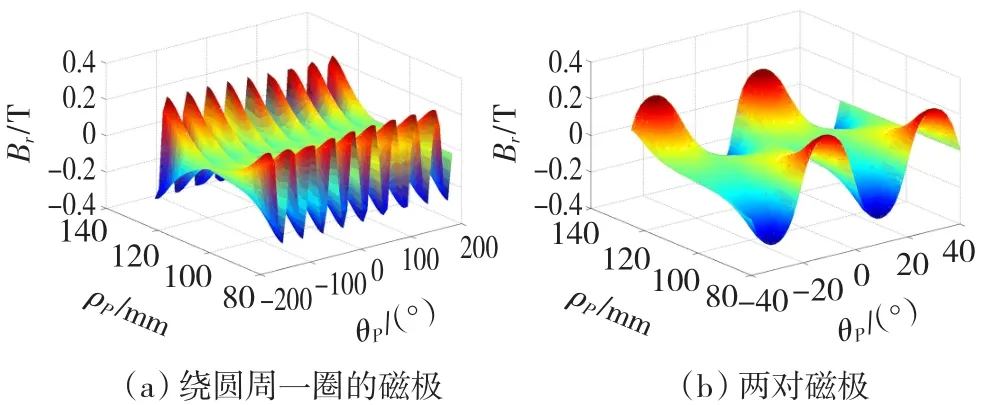
图3 径向磁场三维空间分布Fig．3 Three-dimensional spatial distribution of the radial magnetic field

3.3 周向磁感应强度Bθ的变化曲面图

如图4所示，周向磁感应强度的三维空间分布呈幅值大小不一的周期分布，每一个周期的分布形状如“V形”，其幅值大小在－0.5～0.5T之间变化。由图4(b)可知，一个周期内，从内径到外径周向磁感应强度的变化量很小，在平均半径面上相比两端略有增加。

图4 周向磁场三维空间分布Fig．4 Three-dimensional spatial distribution of the circumferential magnetic field

4 试验测量

4.1 试验方案

磁场测量装置如图5所示，三维高斯计探头位于主动盘与从动盘之间，并位于气隙的平均厚度平面处。利用此装置先后测量了气隙厚度为4 mm、6 mm、8 mm时气隙厚度中间平面的静态磁场分布。首先将气隙厚度调整为4 mm，其次将高斯计探头置于如图6所示的气隙中间平面上A点，之后保持主动盘和从动盘同步转动一圈，每转过5°记录一次数据，共记录72个数据，然后将探头测点分别径向移动到 B、C、D、E、F、G、H 点，以相同的方法测量不同圆周上的磁场空间分布。各个不同的圆周上的气隙磁场测量完成后，再次调整气隙厚度为6 mm、8 mm分别按上述的方式再次测量。

图5 气隙磁场测量装置现场图Fig．5 Schematic diagram of experiment apparatus

图6 探头测点布置示意图Fig．6 Layout diagram of measurement points

由上述理论计算可知，轴向磁感应强度在气隙磁场中起主要作用。为分析气隙厚度对轴向磁密的影响，将高斯计探头置于图6中CD线段的中点处，并位于气隙厚度的中间厚度平面上。之后将气隙厚度由4 mm移动改变至10 mm，厚度每改变2 mm就将转盘沿圆周方向旋转一圈，通过三维高斯计记录下数据。

4.2 试验结果

在下面所列的空间图形中，三维高斯计的坐标轴方向的含义与上述理论模型中坐标轴规定不同:此处y方向为轴向;x方向为周向;z方向为径向。

4.2.1 气隙厚度为6 mm磁密分布

图7表示气隙为6 mm时磁场沿轴向、径向、分量的空间分布及平面分布图。图7(b)为图7(a)的俯视图，图7(a)、图7(b)中可看出在气隙厚度中间平面处，轴向磁密绕圆周方向出现了9个波峰和9个波谷，并且完全处于对称状态，磁密幅值的大小都在690 mT左右。图7(c)中呈现9个空间形状相似的周期分布，其中一个周期内空间分布形状如“马鞍形”;图7(d)中出现了峰值大小不一的9个波峰和9个波谷，且相邻两个波峰之间形成了“V形”的空间分布形状。从图7(a)～图7(d)的右侧数值对比卡可知，磁感应强度轴向分量为主要磁场分量，磁密幅值远大于其他两个方向上的磁密幅值，分析结果与上一节理论计算结果一致。

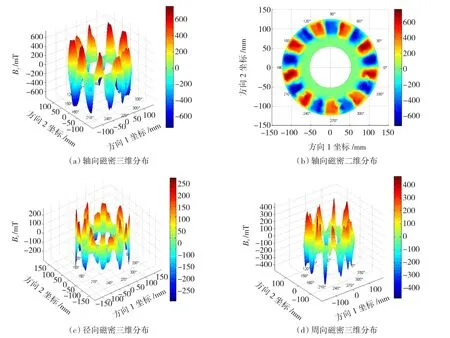
图7 气隙为6 mm时磁密分布图Fig．7 Three-dimensional spatial istribution of the magnetic field for 6 mm air gap thickness

4.2.2 不同气隙厚度对轴向磁感应强度的影响

1)不同气隙厚度下轴向磁密空间分布

图8 不同气隙厚度下轴向磁密三维分布Fig．8 Three-dimensional spatial istribution of the axial magnetic field in the different air gap thickness

图8为气隙厚度在4 mm和8 mm时磁感应强度轴向空间分布图，通过与图7(a)对比，从右侧数值对比卡可知随着气隙厚度的增加，轴向磁感应强度的大小呈现降低的趋势，而且幅值变化很明显，其主要原因由于气隙厚度增大，消耗在气隙中的磁势增加，同时气隙中的磁通量会迅速减少，使得轴向磁密减小。

2)平均直径处轴向磁密变化曲线

取R=(R1+R2)/2的圆周面，图9为气隙厚度为6 mm时的平均直径处轴向磁密曲线，从中可看出图形的波形基本相似，波形中各周期的峰值基本相同，但也有个别峰值略为偏小，主要原因可能是由于永磁盘上个别永磁块的退磁所造成。

图9 气隙为6 mm时中间平面处轴向磁密曲线Fig．9 Axial flux density curve in the middle plane for 6 mm air gap thickness

气隙厚度为4 mm、6 mm、8 mm、10 mm 时，如图10所示，不同气隙厚度时轴向磁密变化曲线，随着气隙厚度的增大，各曲线的峰值变化很明显，呈现迅速下降的趋势。由于盘式异步磁力联轴器的工作原理为通过改变气隙厚度来改变气隙磁场，从而提供给负载端需要的转矩和速度。由上述分析可知气隙厚度变化后轴向磁密变化很明显，正好实现了联轴器设计的要求，达到迅速调节转矩和转速的目的。

图10 不同气隙厚度下轴向磁密变化曲线Fig．10 Axial flux density curves in the different air gap thickness

4.3 结果对比分析

气隙厚度为6 mm时，气隙磁场各分量的幅值理论计算结果与试验测量值如表1所示，试验值与理论计算值具有很好的一致性，但是3个方向的试验值始终都比计算值小，两者也存在一定的误差。从表1可看出误差最大的为径向磁感应强度值，最小的为轴向磁感应强度值，误差产生的主要原因可能有两方面:其一由于理论计算时假象模型是没有退磁漏磁现象的，而实际样机中永磁体是会退磁的;其二试验值圆盘旋转的角度不是由控制系统精确定位的，存在一定的操作误差，致使理论结果与试验值有一定的误差。

表1 试验值与理论值对比表Table 1 Comparison between theoretical results and experimental results

5 结语

本文采用等效面电流法对盘式异步磁力联轴器的三维静态气隙磁场进行了分析，推导出了气隙中任意场点磁感应强度的解析计算公式。然后根据样机模型，利用Matlab编程求解得出了气隙平均厚度平面处的轴向、径向及周向的磁密空间分布。通过对样机的三维气隙磁场试验测量，将实测值与解析结果进行比较表明，发现两者能够很好的吻合，最大误差为13.26%，证明了采用等效面电流法对永磁体进行处理方法的合理性。同时解析结果和试验结果都表明，气隙磁场的轴向分量为主磁场，其磁密幅值远大于其他两个方向上的磁密幅值;当气隙厚度增大时，轴向磁密出现了迅速降低的趋势，这与联轴器通过调节气隙能实现转矩快速变化的设计目的相一致。

［1］唐任远，宋志环，于慎波，等．变频器供电对永磁电机振动噪声源的影响研究［J］．电机与控制学报，2010，14(3):12－17．

TANG Renyuan，SONG Zhihuan，YU Shenbo，et al．Study on source of vibration and acoustic noise of permanent magnet machines by inverter［J］．Electric Machines and Control，2010，14(3):12－17．

［2］袁任光．交流变频调速器选用手册［M］．广东:广东科技出版社，2002:452－458．

［3］刘吉仿，李伟力，程树康．异步变频电机发展综述［J］．微电机，2007，40(6):76－78．

LIU Jifang，LI Weili，CHENG Shukang．Development of variable frequency asynchronous motor［J］．Micromotors，2007，40(6):76－78．

［4］杨超君，李直腾，李志宝，等．高性能磁力齿轮传动扭矩与效率的数值计算［J］．中国电机工程学报，2011，31(32):107－114．

YANG Chaojun，LI Zhiteng，LI Zhibao．Numerical calculation of driven torque and efficiency of a high-performance magnetic gear［J］．Proceedings of the CSEE，2011，31(32):107－114．

［5］WALLACE A，VON JOUANNE A．Industrial speed control:are PM couplings an alternative to VDFs［J］．IEEE Industry Applications Magazine，2001:57－63．

［6］WALLACE A，VON JOUANNE A．Comparison testing of an adjustable-speed permanent-magnet eddy-current coupling［C］//IEEE Pulp and Paper Industry Technical Conference，June 19 －23，2000，Atlanta，USA．2000:73－78．

［7］徐英雷，李群湛，王涛．永磁同步电机空载气隙磁密波形优化［J］．西安交通大学学报，2009，44(4):513－516．

XU Yinglei，LI Qunzhan，WANG Tao．Optimal design of no-load airgap flux density of permanent magnet synchronous motor［J］．Journal of Southwest Jiaotong University，2009，44(4):513－516．

［8］卢晓慧，梁加红．表面式永磁电机气隙磁场分析［J］．电机与控制学报，2011，15(7):14－20．

LU Xiaohui，LIANG Jiahong．Air gap magnetic field analysis of surface-mounted permanent motors［J］．Electric Machines and Control，2011，15(7):14 －20．

［9］刘少刚，邱波．动磁式永磁直线无刷直流电机气隙磁场的解析分析［J］．电机与控制学报，2009，13(S1):62－66．

LIU Shaogang，QIU Bo．Analytic analysis of air gap field of moving-magnet linear permanent magnet brushless DC motors［J］．E-lectric Machines and Control，2009，13(S1):62 －66．

［10］XIONG Guangyu，NASAR S A．Analysis of fields and forces in a permanent magnet linear synchronous machine based on the concept of magnetic charee［J］．IEEE Transactions on Magnetics，1989，25(3):2713－2719．

［11］孟光伟，李槐树．多极永磁无刷直流电动机瓦形磁钢气隙磁通密度的解析计算［J］．电工技术学报，2011，26(9):37－42．

MENG Guangwei，LI Huaishu．Analytical calculation for air gap flux density of multi-pole permanent magnetic brushless DC motor［J］．Transactions of China Electrotechnical Society，2011，26(9):37－42．

［12］杨超君，郑武，李志宝．可调速异步盘式磁力联轴器的转矩计算及其影响因素分析［J］．电机与控制学报，2012，16(1):85－91．

YANG Chaojun，ZHENG Wu，LI Zhibao．Torque calculation of speed-adjustable asynchronous disk type of magnetic coupling and its impact factors analysis［J］．Electric Machines and Control，2012，16(1):85－91．

［13］刘瑞芳，胡敏强，严登俊．永磁电机中永磁体数学模型的分析［J］．微电机，2001，34(1):7－10．

LIU Ruifang，HU Minqiang，YAN Dengjun．The analysis of mathematical model for permanent magnet in permanent magnet electrical machines［J］．Micromotors，2001，34(1):7 －10．