永磁同步直线电机的小波神经网络控制
0 引言
与旋转电机相比,永磁同步直线电机(permanent magnet linear synchronous motor,PMLSM)不需要任何中间转换机构,直接将电能转化为机械能,因而具有结构简单、高精确度、高速度和低维护等优点,在机器人、半导体制造、高精度数控机床和X-Y驱动设备等领域有着广阔的应用前景[1-2]。然而,正是由于其直线结构特点和缺少中间缓冲环节,各种干扰,如推力波动、摩擦力等直接作用于PMLSM,使得PMLSM对干扰更为敏感。在使用PMLSM驱动的高精度数控机床中,干扰会使系统的伺服性能降低,产生振荡增加能量损耗,导致加工的产品表面出现划痕,甚至使产品报废[3]。因此,与旋转电机相比,PMLSM对干扰抑制的质量要求更高,难度也更大。抑制干扰对PMLSM系统的影响,国内外学者进行了大量的研究工作。复合前馈 PID控制方法[4],采用固定参数模型对PMLSM进行速度、加速度补偿,可显著提高系统的跟踪精度,但该方法的跟踪效果受模型参数估计误差影响较大,鲁棒性欠佳,且不能消除干扰影响,其跟踪精度也有限。神经网络自适应逆模型控制方法[5],采用神经网络构建控制对象的逆模型,具有较好的跟踪性和鲁棒性,但该方法中神经网络把PMLSM与干扰作为一个整体进行学习时,往往会忽略对高频干扰部分的补偿,实际上,主要还是对PMLSM系统进行了速度、加速度补偿,系统依然会受干扰的影响。自适应前馈控制与PID控制相结合的控制方法[6],通过对误差信号作频谱分析得出推力波动所包含的主要谐波,在前馈补偿中植入“木马”的方法来减少推力波动对系统影响,具有较好的控制效果,但该方法采用离线方式对误差信号进行傅里叶变换分析时,只能得到干扰的频域信息,而无任何时域信息,因此并不能完全地实现对干扰的在线估计与补偿。
文献[7-8]在建立直线电机干扰观测器模型的基础上,提出了一种有效消除干扰的方法,较好地实现了对直线电机位置的精密控制。
该文采用“分而治之”的思想,在复合前馈PID控制的基础上,提出了一种基于小波神经网络的控制方法:1)用固定参数模型对PMLSM系统进行速度、加速度补偿;2)推力波动、摩擦力等干扰及固定参数模型不精确所造成的误差主要由小波神经网络在线估计进行补偿。所提出的基于小波神经网络控制方法有效地提高了PMLSM系统的跟踪性及鲁棒性,较好地消除了干扰的影响。
1 PMLSM系统模型
PMLSM的干扰主要包括由端部效应、齿槽效应、初级电流和反电动势存在高次谐波及气隙磁密波形非正弦性所引起的推力波动和摩擦力等[9-10]。
考虑干扰影响,PMLSM的电压及动力学方程[11]可表示为
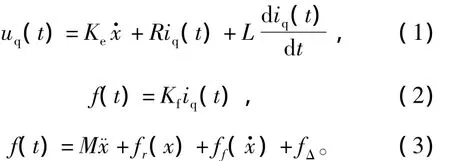
其中:uq(t)、iq(t)分别为PMLSM的q轴驱动电压及q轴电枢电流;f(t)为电磁推力;fr(x) 、ff()为推力波动及摩擦力;fΔ为不确定性干扰,如电机参数扰动和系统噪音所造成的影响等;Ke、R、L、Kf、M、x及x·分别为电机的反电动势常数、电阻、电感、推力常数、动子质量、电机位移及速度。
推力波动fr(x)是与电机位移x有关的周期性波动函数,其模型[12]可描述为

式中:ai为推力波动的幅值;ωi为以电机位移为变量的角速度;φi为相位角。
摩擦力ff()的模型[12]可描述为

其中:fm为静态摩擦力;fc为库仑摩擦力为动子速度;fv为粘滞摩擦系数为经验系数。
此外,式(1)中,相对于电阻R值,电感L值很小,参考文献[6]、[11]与[12],文献将其忽略不计,则PMLSM的动力学方程可表示为

令a=则PMLSM系统模型如图1所示,表现为一个强非线性、多变量的伺服系统。

图1 PMLSM系统模型Fig.1 System model of PMLSM
2 基于小波神经网络的PMLSM控制系统设计
2.1 复合前馈控制
在高精度伺服系统中,复合控制系统可极大地提高系统的跟踪精度。其基本思想为:在系统中引入前馈环节,使之与闭环系统的传递函数之积为1,从而使系统的输出能够完全复现输入[13],其结构如图2所示。
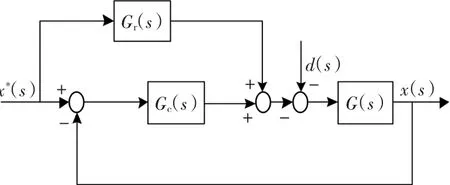
图2 复合前馈控制结构Fig.2 Frame diagram of a feedforward composite control
在图2中,当Gf(s)=1/G(s)时,电机输出位移x(s)可复现位置输入信号x*(s),达到理想的跟踪性能。但实际系统中的模型参数的精确值是不可能得到的,且系统仍然不可避免地受到干扰的影响。
2.2 基于小波神经网络的PMLSM控制系统
在复合前馈PID控制的基础上,利用小波函数对非平稳信号和非线性函数逐步精细描述的强逼近特点,采用小波神经网络在线估计、补偿推力波动、摩擦力等干扰以及补偿前馈环节中,由于采用固定参数模型的不精确所造成的误差。该文所设计的PMLSM控制系统结构如图3所示。
由图3设计控制系统可得,控制电压u=up+uf+ud。up为PID控制器的输出电压值,为系统的反馈误差控制器,e为系统的位置跟踪误差,可得

其中,P、TI和TD分别为比例系数、积分时间常数和微分时间常数。
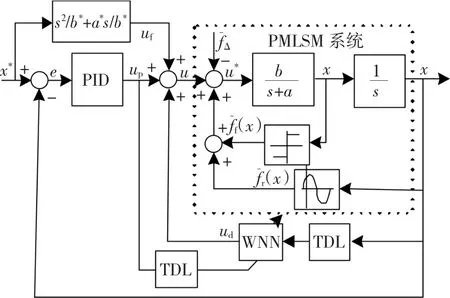
图3 PMLSM控制系统结构Fig.3 Frame diagram of control for PMLSM system
uf为根据电机逆模型,采用固定参数进行速度、加速度补偿电压值,使系统的跟踪精度得到显著提高,其中,a*和b*值可根据电机给定的额定参数计算获得,也可通过实验辨识获得,其输出值为
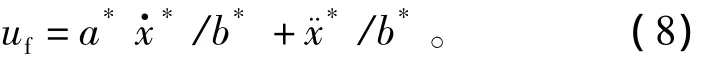
由式(8)可得,控制系统适应于连续可微的位置输入跟踪信号,如正弦波等,如要跟踪不可微信号,如三角波,可用不完全微分法近似代替。
根据PMLSM的动力学方程,如式(6)所示,当uf为系统进行速度、加速度补偿后,系统的跟踪精确度可得到显著提高,则影响系统跟踪性能的主要因素集中于推力波动、摩擦力等干扰以及固定参数模型不精确造成的扰动等,可由小波神经网络WNN的输出值ud进行补偿,其学习信号为反馈误差控制器PID的输出值up,输入信号为电机位移x,目的是使得系统的反馈误差值趋于一个较小值,从而达到进一步提高系统跟踪精度目的。TDL(Tapped Delay Line)为多分头时延单元。因此,在该系统中,WNN的作用主要有两个:1)估计推力波动、摩擦力等干扰,实现在线补偿;2)补偿前馈环节中固定参数模型不精确所造成的误差。
3 小波神经网络的综合问题
3.1 小波函数的选择及对主要干扰的逼近性能分析
小波神经网络中小波函数的选择,目前仍无统一的理论确定哪类小波函数适合做不同网络中神经元的激励函数,主要根据经验和实际情况。该文选取了在函数逼近方面应用较多的一维墨西哥草帽函数[14-15],即


证明:Ψ(x)=(1 -x2)的傅里叶变换为

显然此函数满足
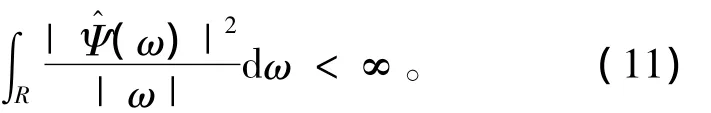
则由式(11)可得Ψ(x)满足母小波函数条件。令

其中,a和b分别为伸缩参数和平移参数。借鉴文献[16]中定理2,通过适当的选择a和b,{Ψmn(x)}亦可以构成L2(R)上的框架,即


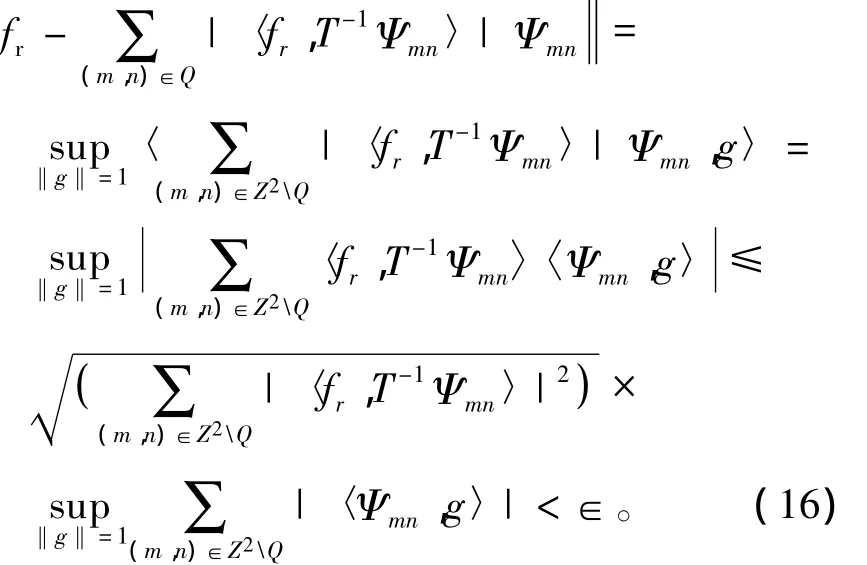
PMLSM中的推力波动为连续函数,故采用一维墨西哥草帽函数构成的小波神经网络可以任意精度实现对推力波动信号的逼近。
证毕。
考察式(5)摩擦模型可得,摩擦力在速度x·=0是不连续的。根据定理1可得,采用一维墨西哥草帽函数构成的小波神经网络可任意精确度逼近摩擦力的连续部分,但对不连续部分则无法有效逼近,其误差主要通过反馈误差控制环节来抑制。
3.2 小波神经网络的结构及学习算法
与径向基函数神经网络结构相同,小波神经网络结构采用3层前向网络。其结构如图4所示。

图4 小波神经网络结构Fig.4 Frame diagram of wavelet neural network
图4 中,输入变量 X=[x1,x2,…,xn]T为电机的位移量,隐含层中的基向量为 ψ =[ψ1,ψ2,…ψm]T,激励函数使用一维墨西哥草帽小波函数得
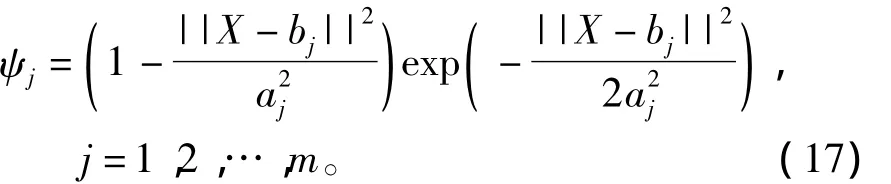
式中:bj=[bj1,bj2,…,bjn]T为网络节点j的移位参数;aj=[a1,a2,…,am]T为节点j的伸缩参数,网络输出层的权向量为 Wm=[ω1,ω2,…,ωj,…,ωm]T。
根据图3中设计的结构图,WNN的输入变量为X=[x(k-1),x(k-2),…,x(k-n)]T,网络输出为

学习信号为反馈误差控制器PID的输出值,即
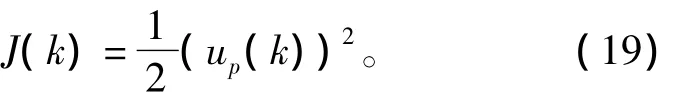
根据反馈误差学习方法[17-18],可避免使用 Jacobian信息。同时根据梯度下降法,输出权值、伸缩参数及平移参数的迭代算法分别如下(η为学习速率,α为动量因子),即
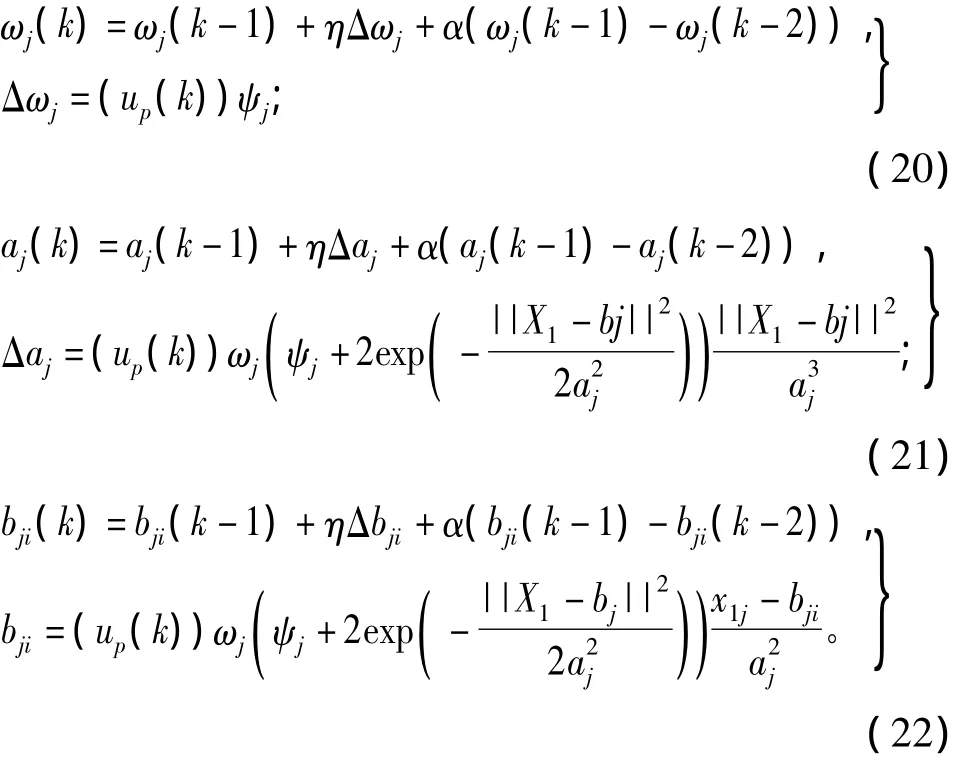
3.3 隐层节点数的确定及参数初始化
与小波函数的选择相同,小波神经网络中隐层节点数的确定和参数初始化尚无统一的理论参考。从理论上讲,隐层节点数越多,网络的逼近精度越高,但网络的结构也越复杂。因此,需要在逼近精度和结构复杂度之间进行折中[16]。参数初始化主要是对伸缩参数、平移参数和权值进行初始化,其大小直接影响网络的收敛性和逼近精度。文献[16]提出伸缩参数初始化主要考虑处理函数的极值,平移参数主要取函数时域边界之间的均值,权值初始化则同一般神经网络完全一样,其收敛速度较快。实际上,只是凭借经验判断,能够保证网络收敛,但并不一定能够保证网络达到较好的逼近性能。
论文采用K-均值聚类算法对网络参数进行初始化训练,可较好地解决网络结构对初值敏感问题,并保证网络达到较好的逼近性能。具体算法步骤可参考文献[19]。
4 实验结果及分析
4.1 实验平台简介
PMLSM实验平台主要包括某微纳科技有限公司自主研制的无铁芯永磁同步直线电机平台、控制箱及PC机组成。
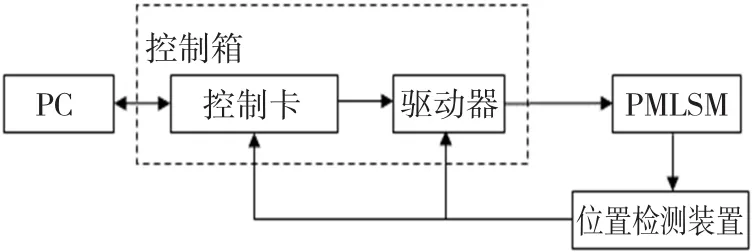
图5 控制系统的硬件原理Fig.5 Hardware block diagram of control system
系统的硬件原理框图如图5所示。硬件实物图如图6所示。在图6中,控制箱中的驱动器采用的是以色列 Elmo公司生产的 Harmonica驱动器。PMLSM的主要额定参数为:动子质量M=0.3 kg,线圈电阻R=19.3 Ω,推力常数Kf=11.71 N/A,反电动势常数Ke=9.6 V·m/s,电感L=2.49 mH,最大运动行程为370 mm。

图6 控制系统实验平台Fig.6 Platform of system experiment
软件资源方面主要是基于TMS320F2812开发的 cSPACE 控制系统,具有 A/D、D/A、I/O、Encoder和快速控制原型开发和硬件在环仿真功能。设计过程中,只需使用Matlab/SIMULINK环境自动生成代码便可完成软件设计,不需要另外编写代码。因此,该平台具有开放性、快速性和易与Matlab联接等诸多优点。
4.2 基于小波神经网络的控制方法实现
基于小波神经网络的控制方法在Matlab/SIMULINK环境下搭建的cSPACE控制算法及运行结果如图7、8所示。图7中小波神经网络补偿器NNC采用了效率高、速度快的C-MEX S-function编程,该算法直接编译下载到cSPACE系统后,便可实现实时控制。

图7 基于小波神经网络的cSPACE控制算法Fig.7 cSPACE control algorithm based on wavelet neural network
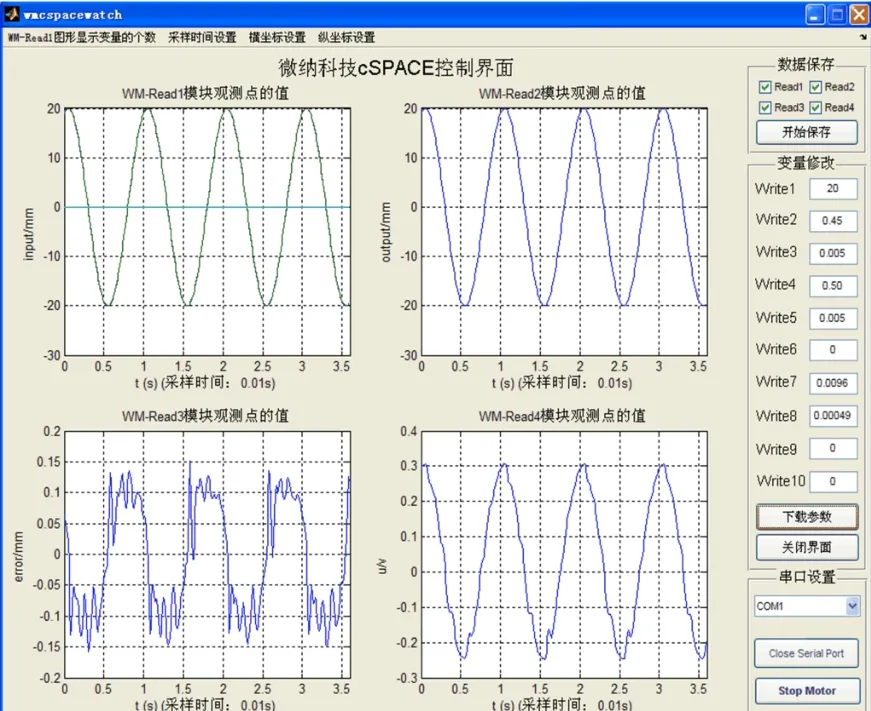
图8 基于小波神经网络的控制方法运行结果Fig.8 Rresults of control based on wavelet neural network
在图7中,输入信号为正弦信号,频率为1Hz,“WM-Write1”用于设定正弦信号的幅值,与图8中“Write1”对应,设置为20 mm;图7中“In2”与“WM-Write3”分别为小波神经网络的学习速率与增益系数,与图8中“Write2”与“Write3”对应,分别设置为0.45与 0.005;图 7中“WM -Write4”、“WM -Write5”与“WM-Write6”分别 PID控制器中的比例、微分及积分系数,与图8中“Write4”、“Write5”与“Write6”对应,分别设置为0.50、0.005与0;图7中“WM -Write7”与“WM -Write8”分别为系统的速度与加速度补偿系数,与图 8中“Write7”与“Write8”对应,根据PMLSM的额定参数的计算值,设置为0.009 6与0.000 49。
在图8运行结果图中,左上角第一个窗口显示的是位置参考输入信号,与图7中“WM-Read1”对应;右上角第二个窗口显示的是电机实际位移,与图7中“WM-Read2”对应;左下角第三个窗口显示的是电机位置跟踪误差,与图7中“WM-Read3”对应;右下角第四个窗口显示的是小波神经网络的补偿电压值,与图7中“WM-Read4”对应。由图8可得,该方法下的位置跟踪误差约为0.15 mm,误差百分比为0.75%。
图9与图10为采用复合前馈PID控制方法下的cSPACE控制算法及运行结果图。

图9 复合前馈PID控制的cSPACE控制算法Fig.9 cSPACE control algorithm of combined feedforward plus PID control
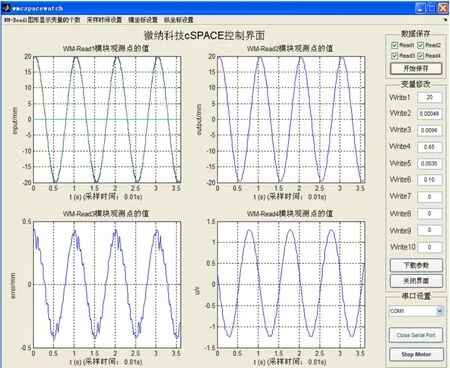
图10 复合前馈PID控制方法运行结果Fig.10 Results of combined feedforward plus PID control
调整PID控制器中比例、微分与积分系数为0.65、0.003 5与 0.10,速度、加速度补偿系数为0.009 6与0.000 49。由图10运行结果可知,采用复合前馈PID控制方法下的位置跟踪误差约为0.44mm,误差百分比为2.2%。
图11与图12给出了采用小波神经网络逆模型控制方法下的cSPACE控制算法及运行结果图。

图11 小波神经网络逆模型控制的cSPACE控制算法Fig.11 cSPACE control algorithm of wavelet neural network adaptive inverse control

图12 小波神经网络逆模型控制运行结果Fig.12 Results of wavelet neural network adaptive inverse control
调整PID控制器中比例、微分与积分系数为0.35、0.004与0,小波神经网络学习速率与增益系数为0.06与0.015。由图12运行结果可得,采用小波神经网络逆模型控制方法下的位置跟踪误差约为0.56 mm,误差百分比为2.8%。
为了便于观察干扰消除情况,对图8中基于小波神经网络控制方法与图12中小波神经网络逆模型控制方法中的位置跟踪误差信号,分别观察其频谱图,其结果如图13所示。表1给出了3种控制方法下跟踪性能的汇总结果。

图13 位置跟踪误差的频谱分析比较Fig.13 Comparisons of frequency analysis for position tracking errors

表1 3种控制方法的跟踪性能比较Table 1 Comparisons of tracking performance
比较图7~13及表1数据可知,采用复合前馈PID控制方法对PMLSM系统的补偿量只是根据PMLSM模型本身进行了近似补偿,并没有对干扰进行补偿,且其跟踪效果受参数估计值精度影响较大;小波神经网络自适应逆模型控制方法不需要估计模型参数值,类似于无模型控制思想,可有效应对模型参数变化,鲁棒性较好,但经频谱分析可知,此方法不能有效消除干扰影响。基于小波神经网络的控制方法采用的是“分而治之”思想,虽然在对PMLSM系统进行速度、加速度补偿时需要对模型参数值进行估计,但参数不精确造成的误差及推力波动、摩擦力等干扰影响可通过小波神经网络在线估计进行补偿,因此受参数估计值影响较小。较前两种控制方法,基于小波神经网络控制的位置跟踪精度能够得到显著提高,且经频谱分析可得该方法能较好地消除干扰影响,从而验证了基于小波神经网络控制的有效性。
5 结论
1)采用“分而治之”思想,在复合前馈PID控制的基础上,引入小波神经网络在线补偿推力波动、摩擦力以及固定参数模型不精确等因素对系统造成的干扰,可使PMLSM系统获得理想的跟踪效果,且能够较好地消除干扰影响。
2)小波神经网络对摩擦力中非连续部分估计效果不佳,导致PMLSM系统仍然受到静摩擦力影响,在后续工作中可加入简单的静摩擦力补偿环节达到完善提高。
3)提出的控制系统适应于连续可微的位置输入跟踪信号。如正弦波等,如要跟踪不可微信号,如三角波,可用不完全微分法近似代替。
4)对小波神经网络中权值参数的初始化问题,仍需作进一步研究。
[1]王丽梅,武志涛,左涛.永磁直线电机自构式模糊神经网络控制器设计[J].电机与控制学报,2009,13(5):643 -647.
WANG Limei,WU Zhitao,ZUO Tao.PMLSM self-constructing fuzzy neural network controller design[J].Electric Machines and Control,2009,13(5):643 - 647.
[2]李腾,刘延杰,孙立宁,等.考虑端部效应的永磁直线同步电机键合图建模[J].电机与控制学报,2011,15(2):71 -75.
LI Teng,LIU Yanjie,SUN Lining,et al.Bond graph approach to the modeling of permanent magnet linear synchronous motor with consideration of end-effect[J].Electric Machines and Control,2011,15(2):71 -75.
[3]郭庆鼎,王成元.直线交流伺服系统的精密控制[M].北京:机械工业出版社,2000:50-72.
[4]侯伯杰,李小清,周云飞,等.直线电机伺服系统的复合前馈 P I D 控制[J].机床与液压,2009,37(2):56 -61.
H0U Bojie,LI Xiaoqing,ZH0U Yunfei,et al.The development of feedforward plus PID controller for linear motor[J].Machine Tool and Hydraulics,2009,37(2):56 -61.
[5]夏加宽,王成元,李皞东,等.高精度数控机床用直线电机端部效应分析及神经网络补偿技术研究[J].中国电机工程学报,2003,23(8):100 -104.
XIA Jiakuan,WANG Chengyuan,LI Haodong,et al.Study of endeffects analysis and NN compensation technique of linear motor for high precision NC machine[J].Proceedings of the Chinese Society for Electrical Engineering,2003,23(8):100 -104.
[6]ZHAO S,TAN K K.Adaptive feedforward compensation of force ripples in linear motors[J].Control Engineering Practice,2005(13):1081-1092.
[7]张代林,陈幼平,艾武,等.基于观测器模型的直线电机干扰抑制技术的研究[J].中国电机工程学报,2007,27(12):14 -18.
ZHANG Dailin,CHEN Youping,AI Wu,et al.Research on disturbance suppression technology for linear motors based on a disturbance cbserver model[J].Proceedings of the Chinese Society for Electrical Engineering,2007,27(12):14 -18.
[8]ZHANG Dailin,CHEN Youping,AI Wu,et al.Force ripple suppression technology for linear motors based on back propagation neural network[J].Chinese Journal of Mechanical Engineering,2008,21(2):13 -16.
[9]宋亦旭,王春洪,尹文生,等.永磁直线同步电动机的自适应学习控制[J].中国电机工程学报,2005,25(20):151 -156.
SONG Yixu,WANG Chunhong,YIN Wensheng,et al.Adaptivelearning control for permanent-magnet linear synchronous motors[J].Proceedings of the CSEE,2005,25(20):151 -156.
[10]ZHU Y W,JIN S M,CHUNG K,et al.Control-based reduction of detent force for permanent magnet linear synchronous motor[J].IEEE Transactions on Magnetics,2009,45(6):2827-2830.
[11]CHEN S L,TAN K K,HUANG S N,et al.Modeling and compensation of ripples and friction in permanent-magnet linear motor using a hysteretic relay[J].IEEE Transactions on Mechatronics,2010,15(4):586 -594.
[12]AHN H,CHEN Y Q,DOU H F.State-periodic adaptive compensation of cogging and coulomb friction in permanent-magnet linear motors[J].IEEE Transactions on Magnetics,2005,41(1):90-98.
[13]刘金琨.先进PID控制及其MATLAB仿真[M].北京:电子工业出版社,2004:55-58.
[14]YLMAZ S,OYSAL Y.A fuzzy wavelet neural network model for system identification[C]//2009 Ninth International Conference on Intelligent Systems Design and Applications,2009,Nov 30 -Dec 2,2009,Pisa,Italy.2009:1284-1289.
[15]程启明,王勇浩.基于小波神经网络的控制方法及其应用研究[J].工业仪表与自动化装置,2004,4:6 -9.
CHEN Qiming,WANGYonghao.A study on the control method and its application based on wavelet neural network[J].Industrial Instrumentation & Automation,2004,4:6 -9.
[16]张茁生,刘贵忠,张宗平.基于小波框架的自适应径向基函数网络[J].自动化学报,2002,28(2):229 -236.
ZHANG Zhuosheng,LIU Guizhong,ZHANG Zongping.Radial basis function networks based on wavelet frames[J].Acta Automatica Sinica,2002,28(2):229 -236.
[17]阮晓钢,丁名晓,于乃功,等.加入预测信息的反馈误差学习模型及其仿真研究[J].系统仿真学报,2006,18(11):3227-3229,3246.
RUAN Xiaogang,DING Mingxiao,YU Raigong,et al.Design and simulation of predictive feedback error learning model[J].Journal of System Simulation,2006,18(11):3227 -3229,3246.
[18]党选举.压电陶瓷执行器的神经网络实时自适应逆控制[J].光学精密工程,2008,16(7)1266 -1272.
DANG Xuanju.Real-time adaptive inverse control based on neural networks for piezoceramic actuator[J].Optics and Precision Engineering,2008,2008,16(7)1266 -1272.
[19]MACQUEEN J.Some methods for classification and analysis of multivariate observations[C]//Proc of the 5th Berkeley Symposium on Mathematical Statistics and Probability.Berkeley,USA:University of California Press,1967:281 -297.

