极限学习机在卫星钟差预报中的应用*

雷 雨 赵丹宁

1)中国科学院国家授时中心，西安 710600

2)中国科学院时间频率基准重点实验室，西安 710600

3)中国科学院大学，北京 100049

极限学习机在卫星钟差预报中的应用*

雷 雨1，2，3)赵丹宁1，3)

1)中国科学院国家授时中心，西安 710600

2)中国科学院时间频率基准重点实验室，西安 710600

3)中国科学院大学，北京 100049

将极限学习机引入卫星钟差预报，对比Sigmoidal、Sine和Hardlim三种激励函数对预报精度的影响，并与传统灰色系统模型和径向基函数神经网络进行比较。结果表明，极限学习机的预报精度优于另外两种模型，其学习速度也快于径向基函数神经网络，且基于Sigmoidal的激励函数最适合于钟差预报。

极限学习机;激励函数;径向基函数神经网络;卫星钟差;钟差预报

1 引言

随着人们对卫星导航和定位精度要求的提高，卫星钟差的预报成为一项至关重要的工作。卫星钟差数据属于一类变化异常复杂的非线性时间序列，而神经网络正是解决复杂非线性映射问题的有效手段。研究发现，将神经网络应用于卫星钟差的预报，比传统的灰色系统模型有更高的预报精度［1－4］。目前在卫星钟差预报中主要采用径向基函数(RBF，Radial Basis Function)神经网络算法，虽然该算法的学习速度较传统的误差反向传播(BP，Back Propagation)神经网络快得多，但由于其在学习过程中需要通过聚类算法迭代选取基函数中心，当学习样本数量较多时导致网络学习是一个非常耗时的过程。极限学习机(ELM，Extreme Learning Machine)作为单层隐含层前馈神经网络(SLFN，Single-Hidden Layer Feedforward Neural Network)的一种新型学习算法，随机产生输入层与隐含层间的连接权值和隐含层神经元的阈值，且在学习过程中无需调整，只需设置网络隐含层神经元的个数，便可获得唯一的最优解。因此具有学习速度快、泛化性能好的优点［5］。

为了缩短神经网络的训练时间，提高预报精度，利用ELM模型进行卫星钟差预报，并利用数值实验讨论了该方法的有效性。

2 ELM的基本原理及其用于钟差预报的方法

已知训练样本{xi，ti}，xi∈Rp，ti∈Rq，i=1，2，…，N，含有L个隐含层神经元(节点)且激励函数为g(x)的SLFN以数学模型的形式可表示为［5］

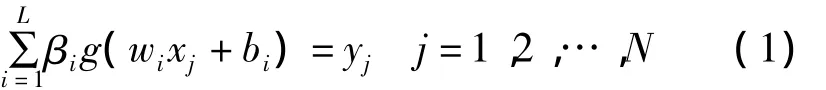
式中，βi表示隐含层第i个神经元与输出层神经元的的连接权值，wi表示输入层神经元与隐含层第i个神经元的连接权值，bi为第i个隐含层神经元的阈值，yj表示第j个输入样本的输出值。

若隐含层神经元个数L与训练集样本个数N相等，则对于任意的w和b，SLFN都可以以零误差逼近训练样本，即

结合式(1)、(2)可写为

式(3)可表示为

式中，H为隐含层输出矩阵，T为输出层输出矩阵。

然而，当训练集个数N较大时，为了减少计算量，隐含层神经元个数L通常取比N小的数，此时SLFN的训练误差可以逼近一个任意ε，即

因此，当激励函数g(x)无限可微时，SLFN的参数并不需要全部进行调整，w和b在训练前可以随机选择，且在训练过程中保持不变。而隐含层与输出层间的连接权值β可以通过

求解最小二乘解获得其解为

式中，H+为隐含层输出矩阵H的Moore-Penrose广义逆，T'是T的转置。

ELM在训练前可随机产生w和b，只需要确定隐含层神经元个数及其激励函数，即可计算出β。

基于ELM的钟差预报的步骤为:

1)确定网络的输入量、输出量。输入量为已知的钟差值，输出量为钟差预报值;

2)根据已有数据，进行训练样本集与验证样本集的划分。其中训练集用来训练网络，验证集用以评估网络泛化性能;

3)将训练样本和测试样本变换到［－1，1］的范围内，以利于提高网络的训练速度［6］;

4)采用MATLAB神经网络工具箱建立ELM，并确定网络的隐含层神经元个数;

5)利用训练集对ELM进行训练;

6)利用训练好的ELM进行钟差预报;

7)将网络输出值进行逆变换，使其恢复到原始数据的量级，并对还原结果进行精度分析。

3 算例分析

实验数据为IGS发布的2010年11月28—30日的GPS精密卫星钟差，采样间隔为5分钟，其中将28、29日两天的数据作为训练样本，30日的数据作为测试样本。考虑到目前在轨GPS卫星有30多颗，限于篇幅，从现有的五种类型卫星钟中各选一颗进行预报，分别是 PRN04(IIA Rb)、19(IIR Rb)、25(IIF Rb)、30(IIA Cs)和31(IIR-M Rb)号卫星，预报跨度为1天。对比不同激励函数对ELM预报性能的影响，对ELM对钟差的预报效果与常用的精度较好的方法进行比较。

3.1 不同激励函数对预报性能的影响

选取Sigmoidal、Sine和Hardlim三种函数作为ELM隐含层神经元的激励函数进行学习，并分析其预报效果。由于隐含层节点个数会导致预报性能存在明显区别，所以该参数的选择是ELM有效进行学习的关键。文中随机将训练集划分为学习样本和测试样本，其中测试样本用以确定隐层节点个数，根据测试样本的均方根误差的大小确定最优隐层节点数，令隐层节点个数以10为步长在［10，280］内递增，采用交叉验证(Cross-Validation，CV)法优化网络［7］。训练过程中测试误差相对于隐层节点个数的变化曲线如图1所示(限于篇幅，这里只给出PRN19号卫星的结果)，由图1可以看出，Hardlim函数对应的测试误差最大，并且随着隐层节点个数的增加，误差逐渐减小，为了更清楚地反映图1所示结果，将Sigmoidal函数和Sine函数的测试误差随隐层节点个数的变化情况单独绘于图2。由图2可以看出，隐层节点个数由10增加至100时，Sigmoidal函数和Sine函数对应的误差较小，在0.2 ns左右，且基本保持稳定;当达到140时，两种函数对应的测试误差急剧增大。需要说明的是，训练误差最小时所对应的节点数即为最优隐层节点个数。

基于三种激励函数的ELM预报均方根误差见表1。由表1可知，使用Hardlim函数作为激励函数时，预报误差非常大，比使用另外两种激励函数的预报精度大约低1～2个数量级;而基于Sigmoidal和Sine激励函数的预报精度在同一个数量级，预报效果较为理想，并且Sigmoidal激励函数比Sine函数更为实用。

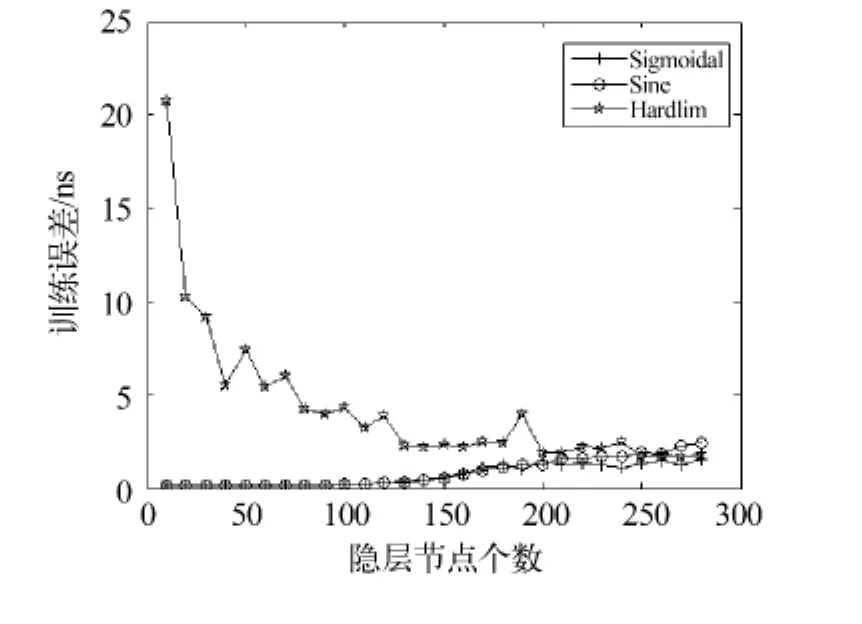
图1 隐层节点个数的确定Fig.1 Determination of number of hidden layer nodes

图2 隐层节点个数的确定(放大图)Fig.2 Determination of number of hidden layer nodes(the amplified figure)

表1 基于不同激励函数的ELM预报精度(单位:ns)Tab.1 Prediction precision of ELM based on different activation functions(unit:ns)

3.2 不同预报方法的比较分析

为了进行比较，使用灰色系统模型和径向基函数神经网络模型进行卫星钟差预报。实验中，对于灰色系统模型，采用29日最后12个历元(时长为1小时)的数据建模;对于RBF神经网络模型，同样将28、29日两天的数据作为训练样本，令隐层神经元个数与训练样本个数相等，并采用CV法优化网络;对于ELM模型，使用Sigmoidal函数作为激励函数。不同预报模型的误差比较如图3～7所示，对应的误差值见表2。

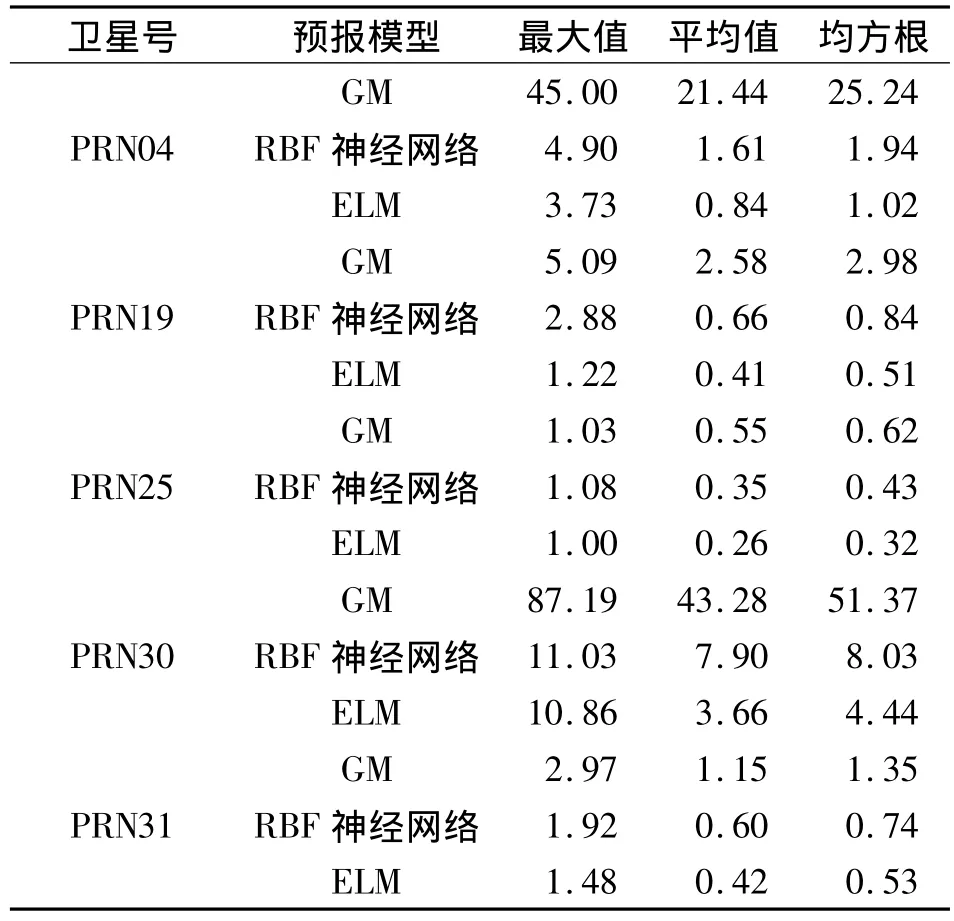
表2 不同预报模型的误差统计(单位:ns)Tab.2 Error statistics of different prediction models(unit:ns)

结合图3～7，分析表2可以看出:

1)RBF神经网络和ELM模型的预报精度和稳定性要明显优于传统灰色系统模型，这是因为神经网络是一种自适应的映射方法，它没有作假设，更不需要事先建立任何数学模型，能避开未知因素的影响，因此能提高钟差的预报精度;

2)ELM模型的预报精度好于RBF神经网络，说明前者的泛化能力比后者强;

3)Block IIA型卫星的星载Rb钟和Cs钟的可预报性远低于其他星载钟，而该型Rb钟的预报精度又高于Cs钟。

为了比较RBF神经网络算法与ELM算法在学习速度、学习能力以及泛化能力等方面上的差异，通过50次实验对同一个训练样本进行学习训练，并对验证样本进行网络验证，计算50次实验结果的平均训练时间、平均训练误差、平均验证时间和平均验证误差(泛化误差)作为两种算法的性能评价标准，对比结果见表3(限于篇幅，仍以PRN19号卫星为例进行讨论)。实验在个人PC上进行，硬件配置如下:CPU为Intel酷睿双核E7500(主频2.93 GHz)，内存为2 G;软件平台为Microsoft Window XP系统MATLAB R2012a编程环境。

由表3可知:

1)ELM相对于RBF神经网络，以较少的隐层节点个数获得与RBF神经网络相似的学习性能，两种算法的训练误差仅相差0.01ns，说明它们的学习能力相当;

图3 不同预报模型的误差比较(PRN04)Fig.3 Error comparison of different prediction models(PRN04)

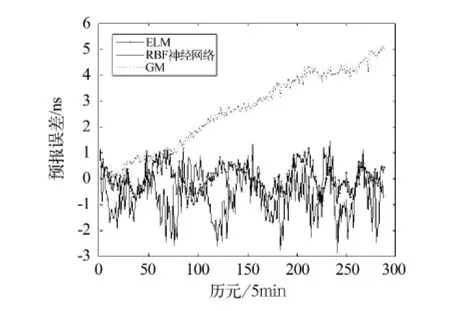
图4 不同预报模型的误差比较(PRN19)Fig.4 Error comparison of different prediction models(PRN19)

图5 不同预报模型的误差比较(PRN25)Fig.5 Error comparison of different prediction models(PRN25)

2)ELM对验证样本的外推误差小于RBF神经网络，说明ELM的泛化能力强于RBF神经网络;

3)在学习速度方面，由于ELM在确定隐层节点个数后不调整任何参数，ELM的学习过程平均耗时仅4.26 s，而RBF神经网络需要不断调整基函数中心，因此需要耗费的时间比ELM的多，平均耗时8.08 s，此外，在对未知样本(验证样本)进行测试时，两种算法的计算速度相当，由此得知，两者速度上的区别仅体现在对训练样本的学习快慢上。

需要说明的是，本文令RBF神经网络的隐层节点个数等于训练样本个数，这样做的目的是简化学习算法，提高学习速度，当然如果想提高网络的学习能力可以通过特定方法选取合适的隐层节点数，但网络的学习算法会变得比较复杂，而且学习速度也会因此随之减慢。另外，值得一提的是，ELM从本质上讲是RBF神经网络的一个特例，即隐层节点数与训练样本数相等，输入层与隐含层间的连接权值和隐含层神经元的阈值是固定的而不是随机产生的，且激励函数为径向基函数时的情况。

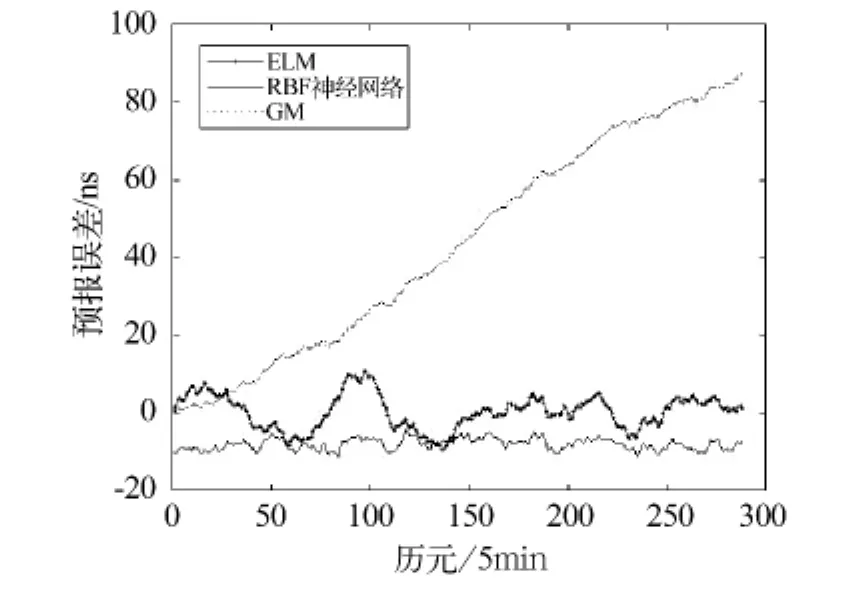
图6 不同预报模型的误差比较(PRN30)Fig.6 Error comparison of different prediction models(PRN30)

图7 不同预报模型的误差比较(PRN31)Fig.7 Error comparison of different prediction models(PRN31)

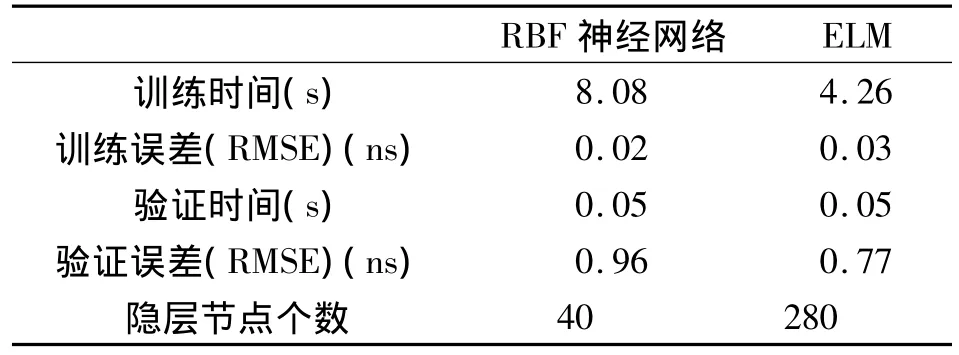
表3 RBF神经网络与ELM性能对比Tab.3 Comparison between performance of RBF neural network and ELM algorithm

4 结论

1)ELM和RBF神经网络算法在卫星钟差预报中具有较高的精度，明显优于传统的灰色系统模型;

2)ELM算法的预报精度不但优于RBF神经网络，且在学习速度上也具有一定的优势;

3)基于Sigmoidal激励函数的预报效果好于Sine激励函数和Hardlim激励函数，其中Hardlim激励函数的效果最差;

4)Cs钟的预报精度远低于Rb钟。

1 崔先强，焦文海.灰色系统模型在卫星钟差预报中的应用［J］.武汉大学学报(信息科学版)，2005，30(5):447 －450.(Cui Xianqiang and Jiao Wenhai.Grey system model for the satellite clock error prediction［J］.Geomatics and Information Science of Wuhan University，2005，30(5):447 －450)

2 郑作亚，卢秀山.几种GPS卫星钟差预报方法比较及精度分析［J］.山东科技大学(自然科学版)，2008，27(4):6－15.(Zheng Zuoya and Lu Xiushan.Comparison and precision analysis of several GPS satellite clock bias prediction methods［J］.Journal of Shandong University of Science and Technology，2008，27(4):6－15)

3 郭承军，滕云龙.基于小波分析和神经网络的卫星钟差预报性能分析［J］.天文学报，2010，51(4):395－403.(Guo Chengjun and Teng Yunlong.Performance analysis of satellite clock bias based on wavelet analysis and neural network［J］.Acta Astronomica Sinica，2010，51(4):395 －403)

4 郭承军，滕云龙.神经网络在卫星钟差短期预报中的应用研究［J］.测绘科学，2011，36(4):198 － 200.(Guo Chengjun and Teng Yunlong.Application of neural network in satellite clock bias prediction［J］.Science of Surveying and Mapping，2011，36(4):198 －200)

5 Huang Guangbin，et al.Extreme learning machine:theory and applications［J］.Neurocomputing，2006，70:489 － 501.

6 王新志，等.基于BP神经网络的厦门集美大桥高程传递的设计与实现［J］.南京信息工程大学学报(自然科学版)，2010，2(5):451 － 454.(Wang Xinzhi，et al.Design and implementation of elevation transmission in Xiamen Jimei bridge based on BP neural network［J］.Journal of Nanjing University Information Science and Technology，2010，2(5):1 451 －1 454)

7 丁常富，王亮.基于交叉验证法的BP神经网络在汽轮机故障诊断中的应用［J］.电力科学与工程，2008，24(3):31－34.(Ding Changfu and Wang Liang.BP neural network application in turbine fault diagnosis base on the cross-validation［J］.Electric Power Science and Engineering，2008，24(3):31－34)

APPLICATION OF EXTREME LEARNING MACHINE IN SATELLITE CLOCK ERROR PREDICTION

Lei Yu1，2，3)and Zhao Danning1，3)
1)National Time Service Center，CAS，Xi’an710600
2)Key Laboratory of Time and Frequency Primary Standards，CAS，Xi’an710600
3)University of Chinese Academy of Sciences，Beijing100049

Extreme Learning Machine(ELM)is employed for predicting satellite clock error.The impact of activation functions on prediction accuracy using ELM is analyzed，including Sigmoidal，Sine and Hardlim functions，and ELM model is compared with the grey system model and radial basis function(RBF)neural network(NN)model.The results show that prediction precision of ELM algorithm is best，and can learn faster than RBF neural network.Moreover，the Sigmoidal activation function is best for clock error prediction.

Extreme Learning Machine(ELM);activation function;radial basis function neural network;satellite clock error;clock error prediction

P207

A

1671-5942(2013)05-0053-05

2013-02-27

国家自然科学基金(10573019)

雷雨，男，1983年生，博士，主要研究方向为GNSS时间传递.E－mail:leiyu@ntsc.ac.cn