基于仿生小波变换和模糊推理的语音降噪算法研究

左东广，王伟军，樊天锁，周 帅，张欣豫

（第二炮兵工程大学 陕西 西安 710025）

在语音通信中，不可避免的会受到各种噪声的干扰，较大的噪声信号可以使语音处理系统的性能急剧下降，甚至处于瘫痪状态。由于语音信号和噪声信号和噪声信号都是非平稳时变的随机信号[1]，使得固定步长的自适应LMS算法在提高初始收敛速度和提高滤波精度上存在不可调和的矛盾，越来越多的变步长LMS算法应用于信号降噪处理中[1-2]。

文中以模糊推理和仿生小波变换为基础，提出了一种新的自适应变步长LMS算法对语音信号进行降噪处理。该算法能够实现在大的误差范围内步长较大，小的误差范围内步长较小，并结合仿生小波变换对语音信号噪声的良好分解能力，达到对语音信号进行滤波的目的。该算法具有较高的收敛精度和良好的跟踪跃变系统能力，实现了非平稳的语音信号在同频段对噪声信号和语音信号的最佳估计和信噪分离。为语音信号的降噪处理技术提供了一种新的方法。

1 基于模糊推理的步长自适应调整算法（VS-FLMS）

语音信号的噪声消除可以通过自适应滤波器实现[3]。自适应滤波的算法有很多，基本的方法有最小均方误差算法（LMS）和递归最小二乘（RLS）算法[4]。步长因子 μ（n）的变化的基本原理是：当误差|e（n）|较大时，步长 μ（n）较大，当|e（n）|较小时，步长μ（n）也变小。这种原则类似于模糊推理的原则，因此可以将模糊推理技术应用于变步长算法的改进。

考虑采用带有中心平均解模糊器、乘积推理机、单值模糊器及高斯隶属函数的模糊推理系统，其在理论上是一个万能的逼近器，能够逼近任意精度的函数。可以通过一个双规则模糊控制系统来说明对步长因子μ（n）的调整过程。

在模糊控制系统中，绝对误差|e（u）|看作模糊控制系统的输入信号，步长因子M（m）作为模糊控制系统的输出信号。以下两条规则构成了模糊推理系统。

规则 A：如果|e（n）|较大，则 μ（n）较大；

规则 B：如果|e（n）|较小，则 μ（n）较小。

为了书写方便，用 x 代替|e（n）|，用 y 代表 μ（n）。 模糊集“较大”与“较小”的两个隶属度函数分别表示为：

式中a1a2＞0，通过中心平均解模糊器和乘积推理机，可以得到模糊控制系统如下：

化简后，得到：

将|e（n）|和 μ（n）代入式（2）后化简得到：

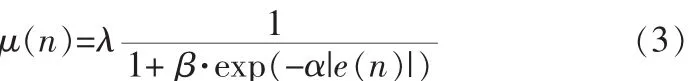
将式（3）中的|e（n）|改为 e（n）2对总体运算不产生太大影响，可得 μ（n）与 e（n）的函数关系式为：

式（4）中 β 用于调节 μ（n）的最小值，α 用于调节 μ（n）与e（n）曲线的倾斜度，λ 用于调节 μ（n）的最大值。

根据万能逼近原理[5]，只要选择恰当的隶属度函数和模糊原则，就可以得出μ（n）与e（n）的非线性函数表达式，用任意的精度去逼近一切 μ（n）与 e（n）的连续性函数，保证了VS-FLMS算法的收敛速度和收敛精度。

2 仿生小波变换法

在对语音信号进行处理的过程中考虑人耳对语音信号的感知特性[6]。小波分解过程中结合人耳的临界带宽并不能较好地反映人耳对语音信号的幅度以及频率的感知特性，考虑采用仿生的小波变换法[7]进行语音信号的信噪分离。

仿生小波变换（BWT）是将人耳的耳蜗机理和小波变换相结合的一种基于生物模型的自适应时频分析方法。相比于一般的小波变换，它在时频域的尺度不仅可以根据信号的频率进行调节，还可以随着信号的瞬时幅度以及一阶微分系数自适应调节。在一般的小波变换中[8-9]，母小波函数h（t）必须满足容许条件，因此可以用其包络函数（t）来表示，即

式中 ω0=2πf0，f0为 h（t）的窗中心频率。 信号 f（t）的小波变换为：

式中a与τ分别表示尺度和时间因子。仿生小波变换引入调整因子T到小波变换的母函数中[10]，即：

其中调整因子T是Gigure的主动听觉模型引入的，它的定义为：

式中fBWT（τ，a）表示时间 τ与尺度 a下的仿生小波系数，G1与G2分别表示人耳中耳蜗的两个能动因子，SBWT表示为饱和因子，Δτ表示计算步长，仿生小波变换可表示为：

仿生小波变换比一般的小波变换具有明显的优点，但是调整因子的公式过于复杂，降低了该算法的实时跟踪能力。通过对Morlet母小波的研究，表明仿生小波变换与基本小波变换之间存在以下的关系：

式中 fBWT（τ，a）表示仿生小波变换的系数，fWT（τ，a）表示一般的小波变换的系数，T0表示母小波函数的常量。

3 基于仿生小波变换和模糊推理变步长自适应滤波语音降噪算法

用小波变换法区分有用信号和噪声信号的方法有很多[13]，主要有：基于小波变换的模的极大值原理消噪法、小波阈值消噪法以及基于小波变换域内系数相关性消噪等[11]，但是当有用信号和噪声信号在重叠频谱时，这些方法虽然能实现信噪分离，提高信噪比，但是不能实现对噪声信号的最优估计，很难实现最优滤波。文中结合模糊推理与仿生小波变技术，提出了基于仿生小波变换和模糊推理变步长自适应滤波语音降噪处理算法，其模型如图1所示。

图1 算法结构模型Fig.1 Algorithm structure model

图中 N=[n0，n1，…，nM-1]T表示输入信号 x（n）经过仿生小波变换法分离出来的噪声分量，M表示滤波器的阶数。算法的主要流程如下：

1）对含噪声的语音信号x（n）进行仿生小波变换

对含噪声的语音信号进行预处理后，进行仿生小波变换，得到含噪声的小波系数。

设 x（n）=s（n）+v0（n），式中 x（n）表示含噪声 语音信号，s（n）表示语音信号，v0（n）表示噪声信号。 含噪声语音信号经过仿生小波变换后，得到：

式中fBWTT为含噪声语音信号经过仿生小波变换的系数。

经过仿生小波变换后，有用的语音信号表现为低频信号，噪声信号为高频信号，通过阈值处理的方法去掉低频信号，保留高频的噪声信号，作为自适应抵消器的输入信号。仿生小波变换的原理框图如图2所示。

图2 仿生小波变换的原理图Fig.2 Schematic of the bionic wavelet transform

利用小波阈值处理方法的基本步骤如下：

①对语音信号进行一维的分解：选择一个小波，同时确定分解的层次J，然后对语音信号进行J层分解。

②小波分解高频系数的阈值压缩，选择恰当的阈值和阈值函数，对第一层到第J层的高频系数进行阈值压缩，分解出其中的噪声成分。阈值的取值为：

2）对分解后的小波系数进行基于模糊推理的变步长自适应滤波

自适应滤波器的输入信号为 N=[n0，n1，…，nM－1]T，滤波器的输出信号为：

误差信号为：

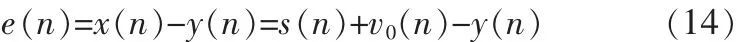
均方误差LMS算法的迭代公式为：

将式①代入②、③可得：

当误差信号的均方值最小时，即E[e2（n）]最小时，输出信号e（n）逼近语音信号 s（n），通过上式不断调整滤波器的抽头权值，使E[e2（n）]达到最小，这时滤波器的权系数即为最佳权值。

4 实验验证和结果分析

实验中采用Morlet函数作为仿生小波的母小波，汉宁窗为窗函数，变换尺度设为a=20，取T0=0.000 073 28，G1=0.62，G2=72.84，自适应滤波器 M=16，μ=0.005。

在语音库中截取一段基本的语音信号作为样本，采样频率为 16 kHz，加入高斯白噪声 v0（n）（0，），通过调整噪声的方差来调整输入信号的信噪比，范围在－5～5 dB。信噪比为－5 dB时的仿真结果如图3所示。

图3 语音降噪效果对比图Fig.3 Voice Noise Reduction effect comparison chart

表1给出了信噪比为－5～5 dB的含噪声语音信号经过3种降噪方法后的信噪比情况。

其失调量的对比图如图4所示。

通过图3中的3种降噪处理方法和表1的数据的对比，文中提出的降噪处理方法明显地优越于其他2种方法，信噪比有很大的提高，文中的方法比单一的自适应滤波法和仿生小波变换法的信号降噪效果都为明显，表明了该算法在语音降噪处理方面的效果是很明显的。

表1 3种方法的信噪比对比图Tab.1 Three ways SNR comparison chart

图4 失调量对比图Fig.4 Comparison chart of the offset amount

5 结 论

文中通过仿生小波变换对语音信号进行信噪分离，将其输出作为模糊推理变步长自适应滤波器的输入进行语音信号的降噪处理，提出了一种基于仿生小波变换与模糊推理变步长自适应滤波器的语音降噪算法。该算法具有较高的收敛精度和良好的跟踪跃变系统能力，实现了非平稳的语音信号在同频段对噪声信号和语音信号的最佳估计和信噪分离。为语音信号的降噪处理技术提供了一种新的方法。

[1]赵力.语音信号处理[M].2版.北京：机械工业出版社，2010：63-68.

[2]孙恩昌，李于衡，张冬英，等.自适应变步长LMS滤波算法及分析[J].系统仿真学报，2007，19（4）:3172-3175.

SUN En-chang，LI Yu-heng，ZHANG Dong-ying，et al.Variable step size LMS adaptive filtering algorithm and analysis[J].Journal of System Simulation，2007，19（4）:3172-3175.

[3]曹斌芳，李建奇.强噪声背景下的语音信号提取研究[J].噪声与振动控制，2008，28（4）:145-148.

CAO Bin-fang，LI Jian-qi.Voice signal extraction in the context of strong noise[J].Noise and Vibration Control，2008，28（4）:145-148.

[4]Haykin S.Adaptive filter theory[M].Fourth Edition.北京：电子工业出版社，2006:342-347.

[5]陆光华，彭学愚，等.随机信号处理[M].西安：西安电子科技大学出版社，2003:163-167.

[6]韩纪庆，张磊，郑铁然.语音信号处理[M].北京：清华大学出版社，2004:54-57.

[7]龚亮，张艳萍.基于掩蔽效应的改进型自适应语音增强算法[J].南京信息工程大学学报：自然科学版，2010，2（6）:529-532.

GONG Liang，ZHANG Yan-Ping.Based on the masking effect of improved adaptive speech enhancement algorithm[J].Nanjing University of Information Science and Technology：Natural Science，2010，2（6）:529-532.

[8]Chen S H，Wang J F.Speech enhancement using perceptual wavelet packet decomposition and eager energy operator[J].Journal of VLSI Signal Processing，2004，36（2）:125-139.

[9]Loizou H Y，Philipos C.Speech enhancement based on wavelet threshold the multilayer spectrum[J].IEEE Trans on Speech and Audio Processing，2004，12（1）:59-67.

[10]杨玺，樊晓平.基于仿生小波变换和自适应阈值的语音增强方法[J].控制与决策，2006，21（9）:1033-1036.

YANG Xi，FAN Xiao-ping.Bionic wavelet transform and adaptive threshold-based voice enhancement method[J].Control and Decision，2006，21（9）:1033-1036.

[11]张晓宁，孙丽君.一种改进的小波阈值信号去噪方法[J].电子科技，2012（11）：15-17，24.

ZHANG Xiao-ning，SUN Li-jun.An improved method for wavelet threshold signal demonizing[J].Electronic Science and Technology，2012（11）：15-17，24.