词类共现频率的MapReduce并行生成方法
程兴国,肖南峰
(华南理工大学计算机科学与工程学院,广州 510640)
在语言学中,语料库(corpus)指大量文本的集合。库中的文本(称为语料)经过整理通常具有既定的格式与标记,特指计算机存储的数字化语料库。
语料库是语料库语言学研究的基础资源,也是经验主义语言研究方法的主要资源,应用于词典编纂、语言教学、传统语言研究、自然语言处理中基于统计或实例的研究等方面。词类共现是其研究内容之一,词类共现频率以共现矩阵的形式表达[2]。
共现矩阵是一个n×n的方阵,n是所需处理的语料中的单词数(不同单词的数量)。矩阵元素mij的值代表单词wi和wj的共现(共同出现)次数。wi,wj共现定义为:wi,wj在指定的上下文范围中同时出现。上下文的范围可以有各种定义,例如同一个句子、同一个段落、同一个文档或是同一个由连续k个单词构成的序列(k的值也是可以定义的)。由于共现关系是对称关系,因此m的上三角阵与下三角阵是相同的[3]。
共现矩阵的空间开销是O(n2),其中n为词汇表(vocabulary)的大小(即不同单词的数量)。根据数据集的不同,词汇表的大小也会有差距:英语语料库中可能包含几万个词汇,而对于Web规模的语料库则可能有几十亿大的词汇表。如果词汇表不大,共现矩阵能放入单机内存中处理是最好不过的。但是大的语料数据往往有很大的词汇表,以至于共现矩阵过大无法放进内存。虚存的使用会降低算法性能,即使压缩能将共现矩阵的空间开销降低一些,这种基于单机、主存的处理模式仍是有上限的。本文基于MapReduce模型实现共现矩阵的计算算法,具有良好的可扩展性,能处理大规模语料数据。
1 MapReduce编程模型
MapReduce模型是Google实验室提出的分布式并行编程模型或框架,它能组织集群来处理大规模数据集,成为云计算平台主流的并行数据处理模型。Apache开源社区的Hadoop项目用Java语言实现了该模型[4-5]。
MapReduce编程模型的基本思路是将大数据集分解为成百上千的小数据集splits,每个(或若干个)数据集分别由集群中的1个节点(一般是一台普通的计算机)并行执行Map计算任务(指定了映射规则)并生成中间结果,然后这些中间结果又由大量的节点并行执行Reduce计算任务(指定了归约规则),形成最终结果。图1描述了MapReduce的运行机制。在数据输入阶段,JobTracker获得待计算数据片在NameNode上的存储元信息;在Map阶段,JobTracker指派多个TaskTracker完成Map运算任务并生成中间结果;Partition阶段完成中间结果对Reducer的分派;Shuffle阶段完成中间计算结果的混排交换;JobTracker指派Task-Tracker完成Reduce任务;Reduce任务完成后通知JobTracker与NameNode以产生最后的输出结果。MapReduce详细执行过程如图1所示[6]。
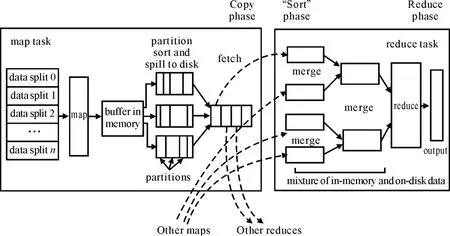
图1 MapReduce详细执行过程
2 词类共现频率的MapReduce方法
2.1 pair算法
表1展示了一种基于pair的MapReduce共现矩阵计算算法(以下简称为pair算法)。

表1 pair算法伪代码清单
mapper接受(docid,doc)对作为输入,对于每个共现对(w,u)都产生一个输出key-value对(见表1的第5行)。这里采用直观的二层循环的方式完成:第1层循环遍历所有单词;第2层循环遍历所有与当前单词相邻(共现)的单词。如果将共现矩阵看作一张图(graph),这相当于每次输出图中的一条边上的一个计数。
reducer将所有具有相同key值的((w,u),1)相加得出最终的((w,u),s)集合,集合中的每个元素对应共现矩阵中的一个元素,因此这个集合等价于共现矩阵。
2.2 stripe算法
表2展示了一种基于stripe的MapReduce共现矩阵计算算法(以下简称为stripe算法)。

表2 stripe算法伪代码清单
mapper构造当前文档的共现对的过程与表1所示算法类似,也是通过二层循环,但mapper记录与输出数据的方式有了一些变化:对于当前文档的每个单词/术语(term)w,维护一个关联数组H,使得H{u}记录的是共现对(w,u)出现的次数。reduce操作则是对分配到当前reducer的由mapper产生的(w,H)对进行加和合并,最后得到一个(w,H)的集合。对于其中每个元素,w是一个单词/术语,H中存储的是所有与w共现的单词u以及共现对(w,u)出现的次数。这个集合同样等价于共现矩阵。
为了更好地理解stripe算法,下面结合例子来说明。例如,对于如下的共现对输入:
文档 1(1,2)(1,2)(1,3)(2,3)
文档 2(2,4)(1,4)(3,4)
输出共现矩阵(共现对计数):
(1,2)∶2(1,3)∶1(2,3)∶1(2,4)∶1(1,4)∶1(3,4)∶1
stripe模式在mapper内对于当前单词wi维护一个关联数组(可以是哈希表、treemap等k-v结构)H。在H中,k是与wi存在共现关系的单词wj,v是共现对(wi,wj)的计数。例如,对于上面给出的实例,当处理文档1时,mapper有如表3所示的处理过程。

表3 stripe模式算法处理过程
随后,reducer接受(w,[H1,H2,H3…]),合并H1,H2,H3…后输出结果,共现矩阵计算完毕。
2.3 pair算法与stripe算法的比较
pair算法与stripe算法代表了两种从观察集中发现、计数共现事件(在本例中即为从语料库中构造共现矩阵)的方法。这两种算法的思路在很多类问题中都能得到有效应用(例如文本处理、数据挖掘、生物信息计算等)。
直观比较下,基于stripe的算法数据表示更为紧凑,而基于pair的算法会产生比基于stripe的算法多得多的中间结果key-value对。因此执行时基于pair的算法需要排序的元素数更多。
进一步来看,pair算法与stripe算法又是统一的,两者只是记录的粒度不同:pair算法单独记录每一次共现,而stripe算法将满足某种条件的共现记录在一起。
stripe算法工作的前提是对于每个mapper输入((docid,doc)对),其对应产生的关联数组都能放入内存之中,虚存的引入将会大大降低其性能。因此,stripe在词汇表很大的情况下难以胜任,一般处理几个GB的语料数据没有问题,而TB甚至PB级的数据就可能会导致内存溢出。相比之下,pair算法则不存在这个问题。
3 stripe算法内存瓶颈的解决
3.1 分治解决内存瓶颈
在stripe算法中,可以将语料数据的词汇表划分为b个桶(比如通过哈希),这样原stripe就会被划分为b个“子 stripe(sub-stripe)”。这种方法可以解决词汇表很大时stripe算法内存不足的问题。需要注意的是,当b=1时,即为标准的stripe算法;当b=|V|(其中|V|是词汇表中的词汇数)时,stripe算法即等价于pair算法。
单词表很大的情况下,每个文档可能包含的单词量非常多。此时对于每个wi可能都有非常多的单词与之共现。假如对于每个单词wi,与之共现的不同的wj单词数平均是一个相对于词汇表规模的固定比例r(例如1%),那么对于规模为n的单词表,维护一个特定单词wi的H平均需要存储r×n个k-v对。如果H的空间利用率是常数的话(例如50%或100%),那么维护H的空间开销是O(n)。
简而言之,词汇表很大会导致与每个wi共现的不同wj很多,最终导致H变得很大。考虑stripe的应用情境:mapper内维护H,可以得出stripe受限于单机内存容量的结论(一个mapper任务在一台机器上运行)。因此stripe虽然高效,却不能直接应用于词汇表很大的语料数据。
内存瓶颈问题的本质是每个wi需要维护的wj过多,导致H过大,如图2所示。
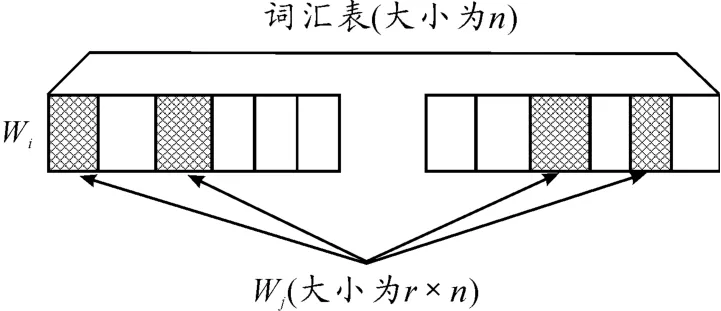
图2 词汇表中wi和wj构成
为简单考虑,先假设这r×n个wj均匀分布在整个词汇表区间里。如果能对该词汇表做划分,那么就可减少一次需要统计的wj的数量,从而减小H。划分情况如图3所示。
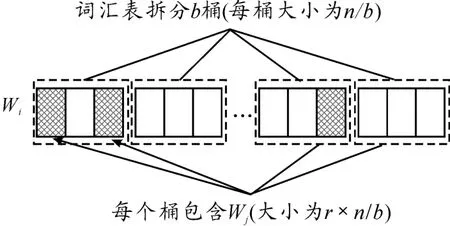
图3 词汇表拆分b桶
将词汇表划分为b个桶后,对于每个桶单独统计就可减小H,而b的值是可变的。这样即使词汇表过大,也可以通过增大b缩小需要一次处理的词汇表大小,从而使得stripe模式能应用至任意大小的词汇表。
3.2 算法实现
分治可以通过在原有的stripe算法上增加一次预处理实现。预处理的功能即划分词汇表,代码见表4。

表4 stripe算法预处理伪代码清单
经过预处理后,数据集被划分为b个子数据集(桶),其中第 i个数据集中只包含(wi,wj),hash(wj)mod b=i。对这b个数据集分别使用stripe算法计算共现矩阵。由于数据集根据wj划分,可知每个数据集的计算结果都是最终全局共现矩阵的其中几列,而数据集之间的计算结果无交集。因此只需要将各数据集的结果简单合并即可得到全局共现矩阵,如图4所示。
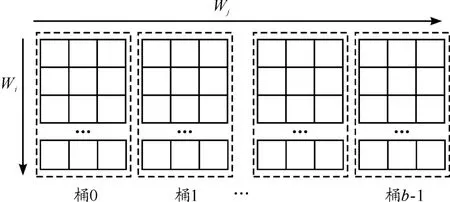
图4 拆分为b个桶示意图
4 实验和结果分析
4.1 环境搭建
实验中云计算平台的结构:1台机器作为NameNode和JobTracker的服务节点,其他8台机器作为DataNode和TaskTracker的服务节点。每台节点硬件配置如下:CPU型号为Intel(R)Core(TM)Duo T8300@2.40GHz;内存为 2GB;硬盘为2TB;基于hadoop-0.20.2版本构建集群。
4.2 实验对照
为达到对照的效果,分别进行pair算法、stripe算法(下称算法1)和分桶的stripe算法(下称算法2)。算法2中,桶的个数分别为40和80个,取得的实验数据如表5所示。
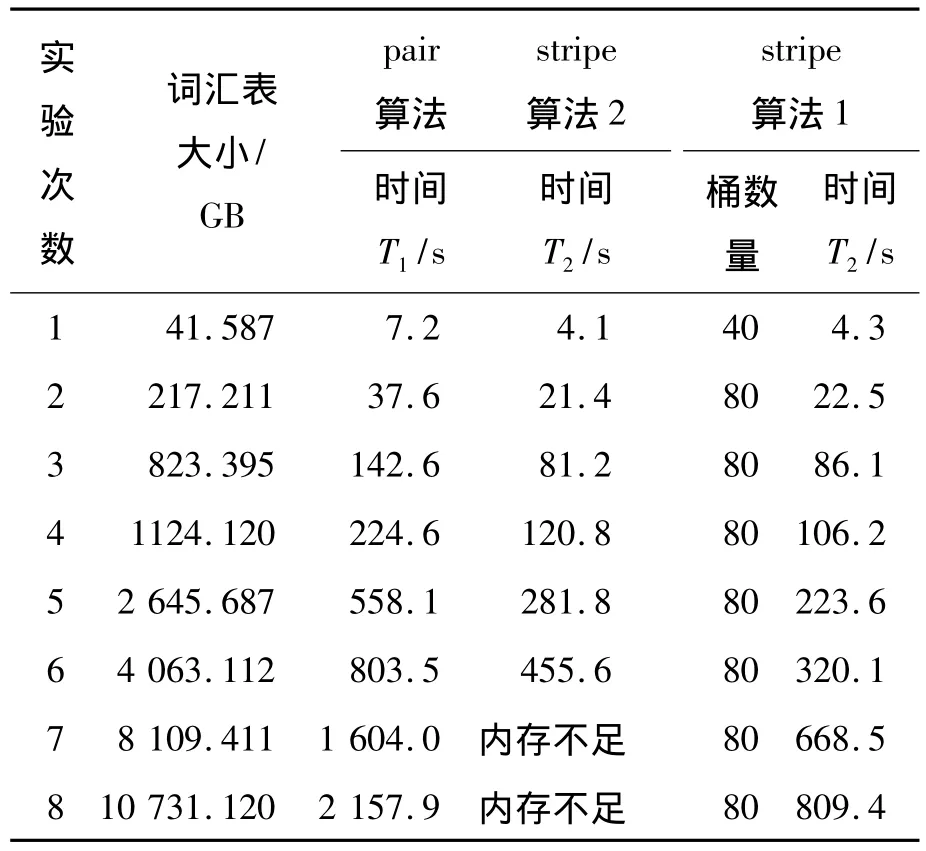
表5 对照实验数据
从表5和图5可以得出:pair算法较stripe算法性能差,并且随着词汇表的增加,其时间急剧增加,直至报内存不足;而stripe拆分算法(stripe算法2)较stripe算法1并没有明显的性能优势,反而时间有所增加,原因是算法2增加了一个预处理阶段,耗费了一定的时间;但随着词汇表的增大,算法2的优势逐渐凸显,海量的词汇表时也没有报内存不足,只是时间稍长,如果适当增加集群的大小,时间会有相当程度的降低。
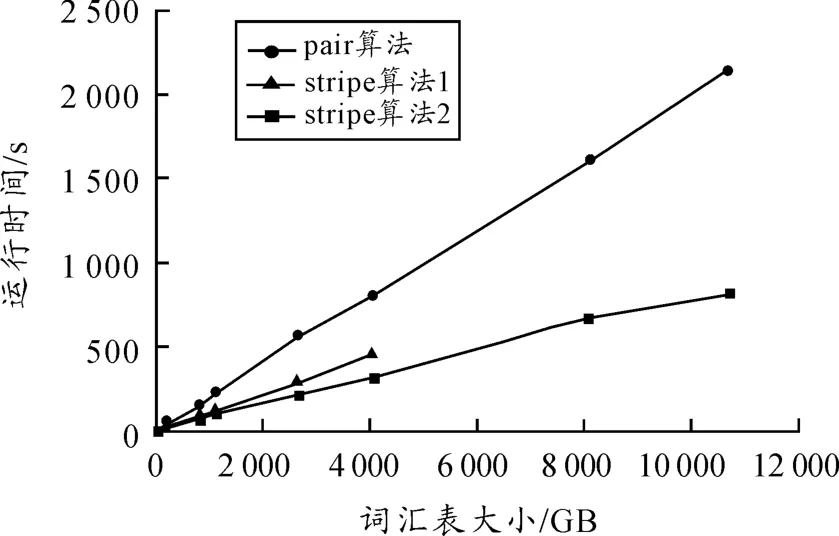
图5 对照实验数据曲线
5 结束语
本文阐述了基于MapReduce模型的两个并行算法:pairs和stripes算法。针对stripes模式在词汇表很大时存在内存溢出问题,本文给出了划分词汇表的解决方法,对输入词汇表进行拆分,此过程也可利用MapReduce模型进行预处理。实验数据证明利用MapReduce的并行性能较好地提高海量语料库中词类共现频率统计的效率和性能。
上述算法可以进行改进,例如都可以应用combiner(Map阶段产生的中间结果合并)。对于stripe算法,应用combiner算法很简单,效率也很高,只需要合并关联数组即可,且合并的步数不会超过语料数据词汇表的尺寸(因为需要合并的关联数组元素数不会超过语料数据词汇表的尺寸);而pair算法的合并工作量就大很多,它只能合并那些具有相同(w,u)值的((w,u),1)对,而(w,u)的可能取值通常很多。
这两种算法都可以应用mapper内合并。无论具体做法是什么,有一点与使用combiner相同:pair算法产生的中间结果key-value对在key的取值范围内呈现稀疏分布的特征,因此即使对其应用局部合并,能真正合并的项也是很少的。另外,(w,u)的可能取值非常大,也使得pair应用mapper内合并时很有可能遇到内存不足的问题。of Computer and System Sciences
[1]Jimmy Lin,Chris Dyer.Data-Intensive Text Processing with MapReduce[J].Morgan & Claypool Publishers,2010(7):26-28.
[2]冯志伟,自然语言处理的历史与现状[J].中国外语,2008(1):14-22.
[3]杨代庆,张智雄.基于Hadoop的海量共现矩阵生成方法[J].现代图书情报技术,2009(4):23-26.
[4]Apache Hadoop,Hadoop[EB/OL].[2011 - 02 - 15].http://hadoop.apache.org.
[5]Hadoop MapReduce[EB/OL].[2008-12-16].http://wiki.apache.org/hadoop/HadoopMapReduce.
[6]Tom White,Hadoop.The Definitive Guide[Z].OReilly Yahoo Press,2ndedition.

