基于半空间刻度的阵列感应测井仪线圈系误差确定方法

李梦春，王成龙，陈宝，党峰，江有宏，王鲁

(中国石油集团测井有限公司，陕西 西安 710077)

0 引言

通过刻度建立感应测井仪器测量电压与视电导率之间的关系，消除仪器线圈系误差和电子线路误差[1]，以保证仪器测量的准确性。传统双感应测井仪利用串有刻度电阻的刻度环确定刻度系数，通过内刻消除电子线路误差，半空间测量确定线圈系误差[2]。通过实时测量校正阵列感应测井仪的电子线路误差，不同测井公司采用不同的半空间测量方法确定线圈系误差。斯伦贝谢公司的AIT采用两高度(1.2 m和3.6 m)测量方法[3-4]。贝克阿特拉斯公司的HDIL提供2种方法[5]，一种是给定大地电导率，通过2个高度(1.8 m和3 m)测量的差值，然后查寻预先计算的测井响应数据库获得线圈系误差;另一种方法是未知大地电导率，将2种高度测量值传回测井解释中心，中心返回大地电导率，用户再查测井响应数据库获得线圈系误差。哈里伯顿公司的HRAI利用2个高度(1.7 m和6 m)确定线圈系误差。魏宝君等[5-6]推导出阵列感应测井仪在水平和垂直情形时半空间响应解析解，分析大地对刻度系数的影响，给出与Barder方法[3-4]一样的线圈系误差确定方法。阵列感应测井仪线圈系误差的准确性直接影响其在高电阻率地层电阻率测量的适应性。例如200Ω·m地层对应电导率5 mS/m，如果线圈系误差的不确定性是±1%，则电阻率测量值在167～250Ω·m间波动;不确定性提高到±0.5%，波动范围减小为182～222Ω·m。由于测量环境不可避免存在大地影响，目前阵列感应测井仪采用的各种半空间测量方法均不能准确确定线圈系误差，实际使用时存在一些问题。如实际测量高度与数据库的理论高度不一致，或者2种高度测量信号差太小都将影响大地电导率估计的准确性，并导致阵列感应测井仪线圈系误差计算不正确。最简单的方法是将仪器提升足够高，完全忽略大地的影响。但理论计算表明，即使高度达到9 m，最长子阵列的大地影响仍超过0.5 mS/m，实际环境条件很难实现9 m高度测量。本文提出一种基于测井响应数据库的新方法，通过仪器水平放置的操作，就可以准确计算阵列感应测井仪线圈系误差。

1 阵列感应测井仪半空间刻度装置与2种高度测量方法存在的问题

标准的半空间刻度装置见图1。5个矮的木桩用于仪器工程刻度，利用刻度环最终确定仪器刻度系数，阵列感应测井仪的木桩高1.2 m。3个高立的木桩用于吊装阵列感应测井仪。刻度环境20 m范围内要求无大块的金属、高压电线、金属排水管道等，地面上铺有水泥。Barder提出的2种高度测量方法确定阵列感应测井仪线圈系误差的方法[3-4]是预先计算好不同高度的线圈系误差校正图版，然后测量2个高度信号，根据差值从误差校正图版查表计算大地电阻率，将实际测量的高值响应减去图版得到的高值视电导率就是线圈系误差，每个子阵列均用同样的方法。这种刻度方法在实际使用中存在和需要解决如下问题。

(1)实际测量高度与理论模型计算高度的不一致性。实际刻度环境的大地从地面向下不可能均匀分布，与计算大地影响的理论模型不一致，因此，实际测量高度不是理论模型中仪器到空气与均匀大地交界面的距离。

(2)2种测量高度的准确性。AIT和HDIL的2种测量高度分别是1.2和3.6 m、1.8和3 m。当大地电导率较小时，2种高度测量差小于或接近仪器测量误差，很难确定大地电导率。最高高度通常选择测量环境条件能够提供的最高高度，选择最低高度成为关键。

(3)刻度过程中温度变化对测量的影响。刻度时从工程刻度到2种高度测量有一定的时间间隔，故测量值除了受大地影响外，还会受到环境温度变化的影响。

(4)选择合适的高度计算线圈系误差。理论上用最高位置确定大地影响，最高位置测量信号减去大地影响即为线圈系误差;但仪器升高时，线圈系存在一定的机械形变，对短阵列影响尤为明显，致使短阵列的线圈系误差不正确。

根据半空间响应理论计算结果提出一种新的方法，以解决以上问题。

图1 水平放置情况下的阵列感应测井仪半空间刻度模型

2 计算半空间响应数据库

正确计算阵列感应测井仪半空间响应数据库是半空间刻度的基础。使用文献[7]的方法计算不同高度、不同大地电导率的半空间响应数据库(也称大地影响数据库)。大地电导率范围0.01～0.5 S/m(电阻率2～100Ω·m)，包括了各种情况下的大地电导率。当大地电导率小于0.1 S/m时，间隔0.01 S/m;大于0.1 S/m时，间隔0.02 S/m，共30种大地电导率。阵列感应测井仪距空气与大地交界面的高度0.2～15 m，为准确确定等效高度，兼顾测量精度，按照不同高度采用不同采样间隔的方法进行:0～2 m，采样间隔为0.1 m;2～4 m，采样间隔为0.2 m;4～10 m和10～15 m，分别对应采样间隔为0.5 m和1 m，共计46个采样点。实际使用时，根据高度与大地电导率，利用查表双线性插值法确定阵列感应测井仪各子阵列对应的大地影响。

3 半空间刻度新方法

阵列感应测井仪的线圈系由8个双侧布置的三线圈系子阵列组成，发射线圈发射包含3种频率(26.256、52.512、105.024 kHz)的信号，8 个子阵列有选择地接收频率信号，实部和虚部共28个原始测量信号，阵列感应测井仪的最长探头距离发射线圈为1.8 m，最短距离为0.15 m。在进行半空间刻度之前，首先要完成工程刻度与1.2 m高度的线圈系误差测量。

3.1 确定等效高度

半空间刻度的高度是指地面到仪器的垂直距离。图2是理论计算的不同大地电导率时，阵列感应测井仪的6、7、8子阵列测量信号随高度变化曲线。从图2可知，每个子阵列有且只有1个峰值，6、7、8子阵列的峰值所对应的仪器高度分别为0.4、0.5 m和1 m，这里的仪器的高度称为理论高度。假设实际刻度结果与理论计算一致，即阵列感应测井仪线圈系的每一个子阵列有且只有1个峰值，则实际与理论高度之间就可建立对应关系，此时实际测量高度称为等效高度。

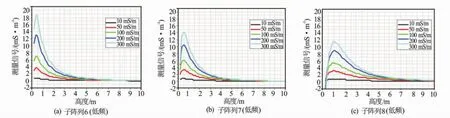
图2 不同大地电导率时测量信号随高度的变化曲线

3.2 确定2种标准高度和计算等效大地电导率

当已知2种高度时，2种高度测量信号之差去除了阵列感应测井仪线圈系误差的影响，仅与大地电导率有关。因此，可以根据2种高度测量信号差从半空间响应数据库查表计算大地电导率。但如果2种高度测量信号之差较小，甚至小于测量信号误差范围，就很难准确计算大地电导率。斯伦贝谢、贝克阿特拉斯和哈里伯顿等公司的第1高度分别是1.2、1.8和1.7 m，第2高度是刻度装置的最高位置。从图2知，这3个第1高度均不是测量信号最大值对应高度。要准确确定大地电导率，2种高度测量信号之差尽可能大。从图2可知，子阵列6、7和8的最大测量信号高度均对应峰值，分别是0.4、0.5和1 m，这就是子阵列6、7和8对应的第1标准高度。第2标准高度选取刻度装置的最高位置。这样得到的2个高度差信号最大，计算大地电导率最准确。图3是子阵列6、7和8的2种高度差信号随大地电导率变化曲线。可用子阵列6、7、8中的任意一个计算大地电导率，根据实际测量信号的稳定性选择其中1个。如均稳定，同时选择，然后取平均值作为大地电导率。

3.3 消除环境温度的影响

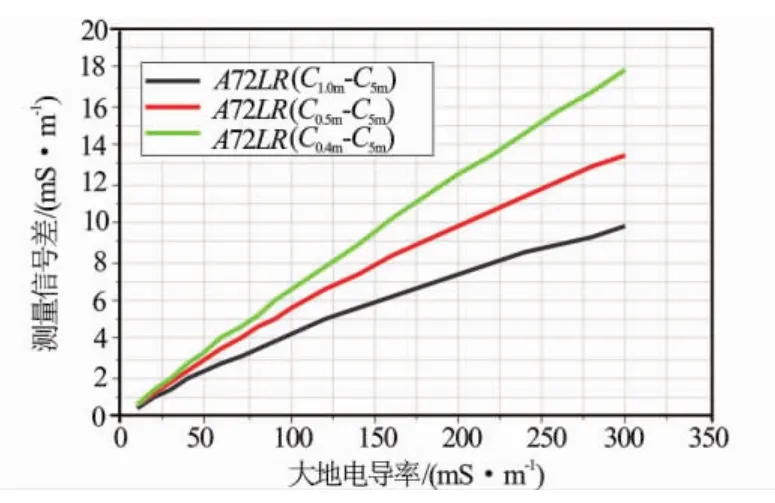
图3 阵列感应测井仪6、7、8子阵列的2种标准高度差信号随大地电导率变化曲线

温度是刻度时常被忽略的因素。刻度环境的温度时刻在变化，工程刻度确定刻度系数需要一定时间。当线圈系受温度影响较大时，如果不进行温度校正，测量信号除了高度和大地影响外还受温度影响，由此计算的大地电导率将不准确，最终影响线圈系误差计算的准确性。因此，在不同高度测量时，测量信号要进行温度校正，校正到刻度时的温度。

3.4 确定计算线圈系误差的基准高度

理论上任意高度均可作为计算线圈系误差的基准高度。常规半空间刻度中取最高位置为基准高度，最高位置测量信号减去该高度对应的大地影响作为线圈系误差。实际测试表明这是有问题的。当硬连接的仪器向上拉升时，拉升仪器的3根尼龙绳不可能完全一致，线圈系和电子仪很难保持平行，玻璃钢只要有弯曲，对各子阵列测量值均有不同程度的影响，最高位置的测量值不仅仅是仪器的线圈系误差和大地影响信号之和，而是包含了仪器弯曲造成的影响。图4是某支阵列感应测井仪的7、8子阵列随高度的变化曲线，曲线不是十分光滑，最高位置附近有波动。如果用最高位置测量信号减去该高度大地影响，线圈系误差将不准确。因此计算线圈系误差的基准高度必须选择信号测量稳定的高度。

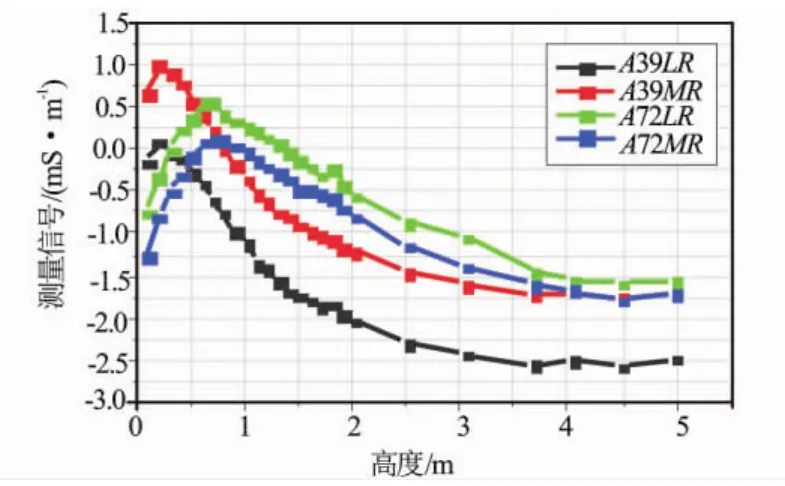
图4 阵列感应测井仪7、8子阵列不同高度实际测量信号

选择仪器固定放置的高度作为半空间刻度基准。此时仪器固定放置在5个木桩上，测量信号稳定，该位置同时也是工程刻度位置，该位置减去大地影响作为线圈系误差稳定可靠。

3.5 半空间刻度新方法的实现

(1)选择用于确定大地电导率的子阵列。通常选择大地影响最大的子阵列确定大地电导率。考虑到实际测量环境比较复杂以及测量信号稳定性，选择子阵列7和8的中低频率信号分别确定大地电导率，然后取平均值作为等效大地电导率。

(2)确定2种基准高度。查半空间响应数据库，子阵列7、8的峰值分别出现在0.5 m和1.0 m处，因此，2个子阵列的第1基准高度分别为0.5 m和1.0 m;第2基准高度由刻度装置能够达到的最高位置决定。

(3)确定理论高度与实际高度差值，计算数据库的第2基准高度。首先将仪器从地面开始升高，每隔0.1 m测量1组数据，直到2 m;大于2 m，每隔0.5 m测量1次，然后绘出随高度变化的测量值，找出峰值出现的高度，该高度是实际的第1基准高度，与理论第1基准高度之差就是理论高度与实际高度的差值。将仪器升至刻度装置最高位置，测量并记录数据。实际最高高度加上理论与实际峰值高度之差就是数据库的第2基准高度。

(4)确定等效大地电导率。根据用2个基准高度从数据库查表获得不同大地电导率时的响应之差，该差值与实际测量差值比较就可确定测量环境对应的等效大地电导率。利用子阵列7和8的中频、低频共4个信号分别计算大地电导率，取平均值作为等效大地电导率。

(5)确定计算线圈系误差的基准高度，计算线圈系误差。如果仪器能够平稳升至刻度装置最高位置，那么选择最高位置作为计算线圈系误差的基准高度。否则，选择工程刻度高度作为计算线圈系误差的基准高度。在该高度时仪器平稳放置在工程刻度装置上，测量信号稳定可靠。根据该基准高度和大地电导率，用数据库插值计算大地影响。从测量信号中减去大地影响即为仪器的线圈系误差。

根据以上步骤设计相应刻度程序。第1次在新环境刻度时必须按以上步骤进行，一旦确定了测量环境实际高度与半空间数据库的理论高度之差，以后再测量时只需测量2个等效基准高度的数据，一个是由最长子阵列8确定的峰值高度位置信号，另一个是刻度装置最高位置信号，刻度程序将自动计算扣除刻度环境影响后的线圈系误差。测量数据必须经过温度校正。

4 实际仪器的半空间刻度测试

根据上述方法先后完成10支仪器的半空间刻度测试。图5是某支仪器实测半空间响应与理论计算曲线的比较，其中实测数据去除了线圈系误差。图5表明实际高度与理论高度相差约0.2 m，调整该高度后，理论结果与实际结果十分吻合。

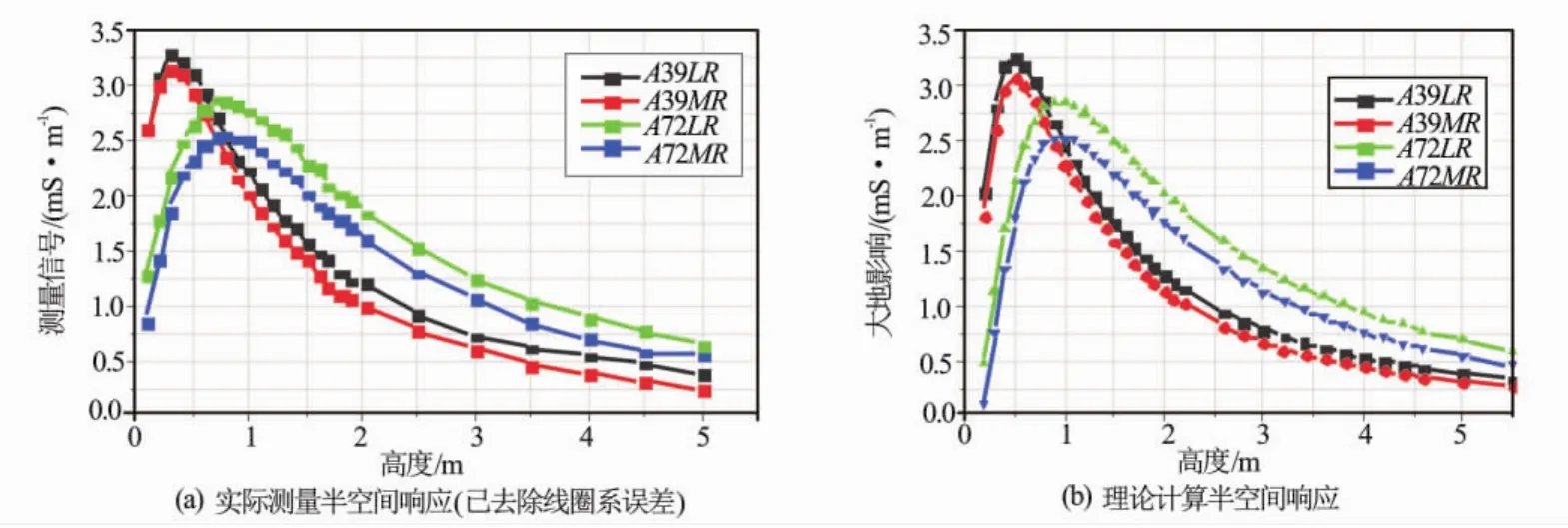
图5 某仪器半空间刻度实测曲线与理论计算曲线比较

图6是试验井测量数据直接使用1.2 m高度刻度[见图6(a)]和使用半空间刻度[见图6(b)]处理结果，同时给出了双感应仪器的测量结果。图6表明，在257～266 m的层位直接使用1.2 m高度刻度处理测井数据，合成曲线分开明显，且显示地层电阻大于100Ω·m，明显与双感应测井仪不一致，但仪器采取半空间刻度后，再次对测井数据进行处理，阵列感应测井仪的合成曲线与双感应测井仪完全一致，且读数合理，曲线分开现象得到明显改善，证明运用半空间刻度的方法完全可以消除阵列感应测井仪线圈系的误差。

图6 某仪器的试验井测井处理结果

5 结论

(1)针对阵列感应测井仪刻度确定线圈系误差中存在的问题，提出一种基于半空间测量的线圈系误差确定新方法。

(2)新方法解决了实际测量高度与半空间响应数据库理论计算高度不一致、合理确定大地电导率、测量信号温度影响以及确定计算线圈系误差基准高度等问题。

(3)通过仪器测试与试验井数据处理，验证了新方法的有效性，且该方法完全可以推广应用于其他阵列感应测井仪线圈系的误差确定。

[1]仵杰，牒勇，解茜草，等.阵列感应测井仪器MIT的标定研究[J].石油仪器，2009，23(2):19-21，74.

[2]李国玉，马明学，彭智.阵列感应测井仪刻度方法研究[J].石油仪器，2011，25(1).

[3]Barder T D，Vandermeer W B，Flanagan W D.Method for Determining Induction Sonde Error[P]，USP4，800，496，1989.

[4]Barder T D，Hanming Wang.Method for Determining Sonde Error for an Induction or Propagation Tool with Transverse or Triaxial Arrays[P]，US20050143920 A1，2005.

[5]魏宝君，张中庆，张庚骥.半空间水平放置阵列感应测井仪的刻度及误差校正[J].西南石油大学学报，1998，20(3).

[6]魏宝君，张庚骥.半空间垂直放置阵列感应测井仪器的刻度及误差校正[J].西安石油学院学报，1999，14(3).

[7]仵杰，王昭.基于COMSOL Multiphysics的阵列感应测井半空间响应计算和误差校正[J].国外测井技术，2012，(2):27-30.