C#矩阵类的实现及其在测量平差中的应用

朱 杰 吕 伟 赵显富

(1南京信息工程大学遥感学院，南京 210044)(2中国石化石油物探技术研究院，南京 211103)

C#矩阵类的实现及其在测量平差中的应用

朱 杰1吕 伟2赵显富1

(1南京信息工程大学遥感学院，南京 210044)
(2中国石化石油物探技术研究院，南京 211103)

摘 要:为了简化测量平差程序，优化矩阵在平差程序中的应用，采用面向对象C#语言编写了矩阵类.测量平差的数学模型具有某些共性，首先将这些共性归纳提取出来;然后按照字段、属性和方法对这些共性进行分类、设计;最后利用C#语言强大的类库支持实现程序化并最终封装成一个矩阵类，不同的平差方法可从这一矩阵类进行继承和扩展.用实例对该矩阵类进行了验证，结果表明:C#矩阵类使各种平差模型程序化实现变得更加简易、高效，节省了平差处理的时间，提高了计算结果的正确性.另一方面，程序代码的共享和扩展也更加方便，对其他涉及矩阵运算的领域和行业有借鉴和实用价值.

关键词:测量平差;矩阵类;C#

矩阵运算在许多学科、工程项目等中都有涉及，成为研究和解决实际问题不可少的数学工具，尤其在诸如测量这种需要处理海量数据的学科中.测量平差是测量内业数据处理中非常重要的一个环节［1］.随着计算机的广泛应用，矩阵运算往往是由计算机处理完成.用计算机技术实现平差，既节省了时间，提高了效率，又提高了计算结果的准确性.测量平差方法多样，但从网形、平差的数学模型上都有某些共性，可把这些共性抽象出来，组成一抽象基类，不同的平差方法可从这一抽象基类进行继承和扩展，形成一个完整的测量平差类框架［2］，本文将这些共性提取出来封装成一个抽象基类(即矩阵类)，基类内的方法和属性可以直接被调用，这为不同平差方法的实现打下了基础.C#是专门针对.NET开发的一种安全的、稳定的、简单的面向对象的编程语言.C#综合了VB简单的可视化操作和C++的高运行效率，具有强大的操作能力，它能创建并使用强大的新类型，将实体的特性和能力都封装到一个独立而且自给自足的代码单元中［3］.

1 C#矩阵类的实现

之前人们总是编写许多函数和过程来实现矩阵的各种运算，这给程序代码的复用带来了一定的困难，程序员经常把大量的精力放在重复调试上.面向对象编写的矩阵类不但能存贮数据，而且还能操作数据，数据和方法被封装在一起，一切方法和数据都在矩阵类中自动处理，如图1所示.

图1 矩阵类视图

为了保证矩阵类设计的正确性和使用的稳定性，在设计的方法内还加入了错误报告提示.用户实例化一个Matrix(矩阵类)对象后，可以实现以下主要属性和方法:

1)矩阵对象的行数、列数等基本属性;

2)矩阵对象的基本运算(加、减、乘等)，可实现多个矩阵对象的混合运算;

3)矩阵对象的复杂运算，包括矩阵求逆，矩阵求伪逆等

1.1 矩阵基本属性的实现

由于在测量平差中，数据多为浮点数，为提高计算结果的精度，定义矩阵数组为双精度型(double型)［4］.测量平差计算过程中，考虑到误差方程和法方程计算基本上都是二维数组，因此，矩阵类中定义的数组是二维的.其中误差方程的常数项L可以将其看作是一个(n×1)二维数组.这里主要介绍了矩阵的行、列2个基本属性，见表1.

表1 矩阵的基本属性

属性按可以访问的类型分为3种不同的类型:一是读/写属性，二是只读属性，三是只写属性.考虑到平差数据都是通过系统读入的，因此系统将矩阵类的行列属性设置为只读.

1.2 构造函数的实现

构造函数是类的一种特殊成员方法，它会在创建类的对象实例时被系统自动调用执行，用户调用构造函数来为类对象分配空间，给它的数据成员赋初值，以及其他请求资源的工作.在C#中实例构造函数又分为默认构造函数和非默认构造函数，默认构造由系统自动提供，它仅负责创建对象，而不做任何初始化工作.非默认构造函数在创建对象的同时会初始化类中的成员数据.系统设计的矩阵类设计的是非默认构造函数:

1)指定行列构造函数

public Matrix(int l，int w)，其中 l是矩阵的行数，w是列数.

2)指定值构造函数

public Matrix(double［，］value)，其中 value 是二维数组，将矩阵各元素存储其中.利用矩阵类进行平差计算时首先要将对象初始化，以误差方程中的系数矩阵A为例，采用二维数组初始化矩阵对象，Matrix B=new Matrix(A)，式中对二维数组A进行初始化，此时A的返回类型是Matrix型.

1.3 基本数学运算的实现

系统设计的矩阵类的基本运算包括矩阵之间的加、减、乘、数乘等一些普遍运算方法.在进行矩阵计算之前，首先得实例化2个矩阵对象，然后结合C#中运算符重载的功能，2个矩阵对象就可以进行运算了.以开发的矩阵类中乘法为例说明:

在调用此方法时，首先要实例化矩阵对象，以法方程系数矩阵的运算为例，p为观测值权数组，A为误差方程中的系数矩阵，AT是误差方程系数矩阵转置矩阵(矩阵类设计的方法中包括矩阵转置，文中不详细说明)，Matrix B=new Matrix(A);Matrix P=new Matrix(p);Matrix BT=new Matrix(AT)，代码中“operator*”是C#中重载运算符的标志，那么法方程的系数矩阵即为B*P*BT.

1.4 复杂运算的实现

平差计算除了用到一些基本的矩阵运算，还需要用到矩阵的一些复杂算法，如矩阵求逆、求矩阵的满秩分解、求矩阵伪逆等.这些算法在平差计算中都会涉及到，以下主要介绍了矩阵求逆和求矩阵伪逆的实现方法.

1.4.1 矩阵求逆的实现

在测量平差中，不管采取哪一种平差模型(条件平差、间接平差、附有参数的条件平差、附有限制条件的间接平差)，矩阵求逆是核心［5］.矩阵求逆的方法很多，根据矩阵的特点和逆矩阵的定理，有伴随矩阵法、初等变换法、分块矩阵法、解方程组法等.系统采用了初等变换法求矩阵逆，如果n阶方阵A可逆，作一个n×2n的矩阵(A|E)，在一行上施行初等变换，对A和E施行相同的初等变换，使A化为单位矩阵E.同时E化为A－1.实现方法如下:

1.4.2 矩阵伪逆的实现

在无起始数据的秩亏网平差中，广义逆矩阵起着重要的作用.在线性代数中讨论线性方程组的解时，一般均不涉及带权的问题.但在测量平差中，观测值向量L或未知数向量X往往具有先验权阵P，因此，在讨论线性方程组的解时，必须引入加权广义逆的概念［6］.根据广义逆的概念和定理可知［7］，伪逆(又称Moore-Penrose逆)有唯一解.秩亏网平差的解法常用的方法有:直接解法，附加条件法和转换法等.另一种是广义逆法，即通过求法方程系数阵N的某些广义逆，或求误差方程系数的伪逆，求出其特解.这里使用伪逆算法来解决秩亏问题［8］，这样求出的未知参数有唯一解.求伪逆的方法很多，本文设计的矩阵类采用的是满秩分解法求伪逆.有m×n复矩阵A，秩r＞0，对A施行初等行变换，可得到阶梯形矩阵，然后将阶梯型矩阵转化为行最简形矩阵，最后将满秩分解后的2个矩阵提取出来.其实现方法如下:

2 矩阵类在平差中的应用

水准网是建立高程控制的一种常规方法，在取得合格的外业数据后需要对所建立的水准网进行平差.由于工程规模、所处地理环境及工程本身要求的多样性，要求有适应工程自身特点的多种平差模型来处理不同工程、工程不同建设阶段的观测数据.当前大都测量平差软件都是按照经典平差模型设计实现的，对于像普通秩亏、拟稳秩亏以及加权秩亏的平差模型设计的较少，平差模型不全面，功能较单一.矩阵类的设计很大程度上解决了此类问题，在实现经典平差的基础上，几种秩亏平差能够完全实现，这就大大地促进了平差软件功能的完整性，迎合了工程的多样性和复杂性.以矩阵类在秩亏自由网平差模型［9］应用为例，其实现过程如下.

误差方程及其约束条件:

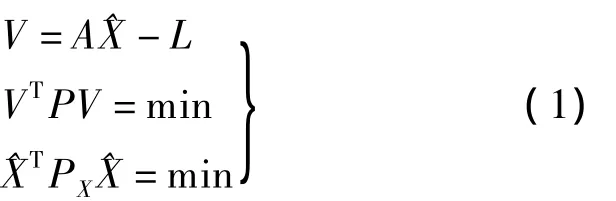
式中，第一式为误差方程，第二式为最小二乘条件，P为观测值权矩阵;第三式为最小范数条件，PX为未知数的权，在秩亏自由网平差中PX=I.

法方程及其解为

对(3)未知数伪逆求解，即

精度估计:

鉴于以上秩亏自由网平差模型，程序代码计算如下:

采用矩阵类后，程序会变得简洁、直观，运行效率也会变高.

3 结语

通过采用面对对象方法设计的矩阵类，实现了矩阵运算在程序中的运用，使程序简单直观、易于掌握理解.随着各项工程、科研项目所需要处理的数据越来越多、越来越复杂，数学方法的使用非常广泛，开发和实现的矩阵运算类应用于一些工程项目中，大大地提高了工作效率，推进了工作进度.因此，矩阵类实用性很大.

［1］陈影，程耀东.基于VC++、ObjectARX的边角网平差系统的设计［J］.物探与化探，2007，31(1):60-61.

Chen Ying，Cheng Yaodong.The designing of the measurement adjustment system on VC++and objectARX［J］.Geophysical and Geochemical Exploration，2007，31(1):60-61.(in Chinese)

［2］谢智颖，李清泉.面向对象的测量平差软件设计与网络化应用［J］.武汉大学学报信息科学版，2003，28(5):605-606.

Xie Zhiying，Li Qingquan.Design of object-oriented survey adjustment software and its online service［J］.Geomatics and Information Science of Wuhan University，2003，28(5):605-606.(in Chinese)

［3］李愈胜，刘卫卫，汪泳.Programming C#3.0中文版［M］.5 版.北京:电子工业出版社，2009:61-62.

［4］王友昆，余章蓉.测量平差矩阵类C#实现［J］.测绘工程，2007，16(5):31-33.

Wang Youkun，Yu Zhangrong.Realization of matrix class in survey adjustment by C#［J］.Engineering of Surveying and Mapping，2007，16(5):31-33.(in Chinese)

［5］郭小龙，周世健.测量平差电算程序中矩阵求逆实现与优化［J］.测绘科学，2004，29(2):74-76.

Guo Xiaolong，Zhou Shijian.Matrix inversion realizing and optimizing by computer programing in survey adjustment［J］.Science of Surveying and Mapping，2004，29(2):74-76.(in Chinese)

［6］於宗俦，于正林.加权广义逆与秩亏网平差［J］.武汉测绘学院学报，1985(1):42-52.

Yu Zongchou，Yu Zhenglin.Weighted generalized inverse and rank-defect net adjustment［J］.Journal of Wuhan Institute of Surveying and Mapping，1985(1):42-52.(in Chinese)

［7］徐仲，张凯院.矩阵论简明教程［M］.北京:科学出版社，2005:141-142.

［8］陶本藻.自由网平差与变形分析［M］.武汉:武汉测绘科技大学出版社，2000:5-12.

［9］张勤，张菊清，岳东杰.近代测量数据处理与应用［M］.北京:中国测绘出版社，2011:20-21.

Realization of matrix class based on C#and its application in survey adjustment

Zhu Jie1Lü Wei2Zhao Xianfu1

(1School of Remote Sensing，Nanjing University of Information Science and Technology，Nanjing 210044，China)
(2Sinopec Geophsical Research Institute，Nanjing 211103，China)

Abstract:In order to simplify the procedure of the survey adjustment and optimize the application of matrix in adjustment procedure，the matrix class based on C#is programmed.The mathematical model of survey adjustment has some commonalities.First，these similarities are generated and extracted.Then，they are classified and designed according to the fields，properties and methods.Finally，these commonalities are programmed and packaged into a type of matrix using a strong library support of C#language.Different adjustment methods can be inherited and expanded from the matrix class.Experimental results indicate that various procedures of the adjustment model are realized more easily and efficiently by applying the C#matrix class.Thus，the time of processing adjustment is saved and the accuracy of the results is also improved.On the other hand，it is convenient to share and expand the program code and there is referential and practical value in other fields and industries involved in matrix operations.

Key words:survey adjustment;matrix class;C#

中图分类号:P207.2;TP31

A

1001－0505(2013)S2-0406-04

doi:10.3969/j.issn.1001 －0505.2013.S2.040

收稿日期:2013-08-20.

朱杰(1989—)，男，硕士生;赵显富(联系人)，男，教授，xfu-zhao@163.com.

基金项目:苏州市科技局基金资助项目(SG201113/20110242).

引文格式:朱杰，吕伟，赵显富.C#矩阵类的实现及其在测量平差中的应用［J］.东南大学学报:自然科学版，2013，43(S2):406-409.［doi:10.3969/j.issn.1001 －0505.2013.S2.040］