基于量子分布估计算法的火力分配问题研究

张 毅， 杨秀霞， 周绍磊

(海军航空工程学院控制工程系，山东烟台 264001)

0 引言

火力分配问题是根据武器攻击的任务，合理进行目标配对决策，并向武器装订相应的决策指令，使攻击效率最高，其属于NP难问题。传统的求解算法，如非线性网络流法、搜索树法等，都基于图论搜索的思想，具有指数级的时间复杂度，当武器及目标数目增加时很难求解［1］。目前，一些学者采用智能优化算法如遗传算法［2］、粒子群算法［3－4］、蚁群算法［5］等对火力分配问题进行了研究，但算法的收敛速度仍然较慢，且难以保证解的精度。为满足实战需求，只能降低最优性要求，求得满意解。针对这一问题，本文在综合考虑武器作战效能和防御效能的基础上，建立了一种用于多武器对抗多目标的火力分配模型，提出了基于量子分布估计算法的火力优化分配方法，并引入一种适于问题求解的编码方法，这种方法可以根据武器目标的数目决定具体的编码方式，同时将模型的约束条件与解的编码结合到一起，提高了算法的运算效率。分布估计算法以全局概率估计模型实现种群的进化，其具有良好的全局优化性能，且进化速度比较快，而量子进化算法的局部寻优能力很强，能够提高搜索精度［6］，本文提出的量子分布估计算法将两种算法的优点相结合，以提高算法的收敛速度及精度，同时给出了自适应量子进化操作算子，提出一种基于量子分布估计算法的火力分配问题求解方法。

1 火力分配的数学模型

1)战术背景:假设有W个火力单位对T个目标进行打击，每个火力单元只能打击一个目标，每个目标可以分配多个火力单元，目标特征用毁伤概率Kij描述，Kij表示分配第i个武器到第j个目标的杀伤概率。

2)分配矩阵:用 R=(Rij)w×T描述，Rij为第 i个火力单元对第j个目标的分配，0为不分配，1为分配。

3)毁伤价值:V(j)为第j个目标将对打击目标产生的期望损伤值。

4)分配期望:最优分配的目标函数是使对目标的摧毁价值指标达到最大。

假设火力单元数目大于目标数目，即W＞T，以最小化目标对系统的损伤为目标函数，要求所有的火力单元必须分配给目标，每个目标至少分配一个武器攻击，则得到多火力单元任务分配模型(N)为

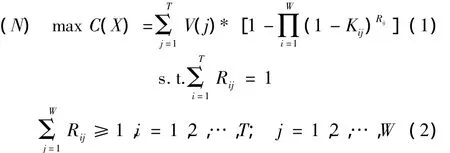
式(1)中，X表示可行的分配方案。

这是一个典型的组合优化问题，且为0－1分配的NP难问题。对于模型(N)，可有(m+1)n种分配方案，在问题规模较大的情况下，采用枚举法得到问题的最优解是不现实的，因此，分配算法对求解的质量和速度要求很高［5］。

2 基于量子分布估计算法的火力分配求解算法

2.1 量子进化算法

目前量子计算理论与进化算法相结合的量子进化算法的研究引起越来越多的学者关注，并被成功地用于背包问题、数值优化等多个领域［7－8］。量子进化算法可看作是一类特殊的分布估计算法(Estimation of Distribution Algorithm，EDA)［9］，其采用量子比特概率幅来构建概率模型，通过该模型对问题解空间中可能存在最优解的区域进行估计和描述，并指导搜索。与大多数EDA算法不同，量子进化算法采用多个量子概率模型并行演化搜索，每个概率模型都可以作为一个独立的搜索单元。在量子进化算法中，概率模型的学习是否全面、充分，对算法的探索能力有着重要的影响。量子概率模型学习越充分，量子进化算法对复杂优化问题的寻优能力可能越强。

一个量子位染色体由一个量子位串组成。如前面所述，一个量子位可以表示为一对复数，当一个量子位染色体量子位长度为m时，它可以表示为

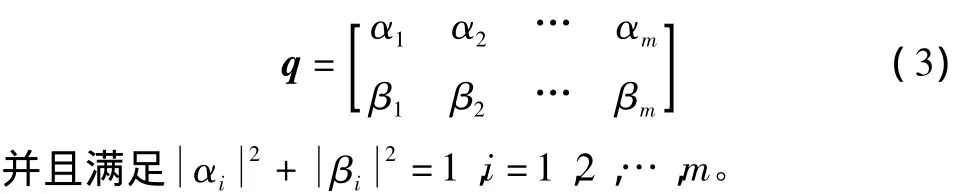
式(3)所描述的是解空间中各个解的取值概率分布，其作用相当于EDA算法中的单变量概率模型。在量子力学中，量子比特的状态还可用相角θ来表示，因此，式(3)所描述的量子概率模型可表示为

量子进化算法实现的基本步骤如下:

1)设进化代数t=0，对种群Q(t)进行初始化;

2)由Q(t)的观测状态产生新的个体P(t)，并对P(t)进行适应度评价，将最优解保存于个体B(t)中;

3)判断终止条件是否满足，若满足，则输出优化结果，否则，令t=t+1，使用量子门更新种群Q(t)，然后转移到步骤2)。

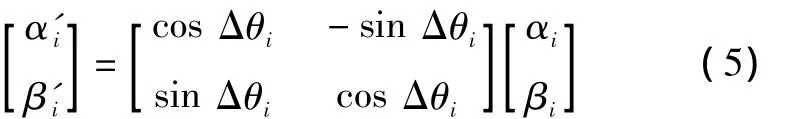
式中，α′i、β′i(i=1，2，…，n)表示采用量子旋转门更新操作后量子位染色体的取值。采用式(5)的模型编码，旋转算子可简化为

式中，Δθi表示量子旋转门的旋转角度，其大小和方向一般由一个事先设计的调整策略决定，由查表获得。在算法实现时需要多个条件判断指令，且必须逐位计算，不方便以向量或矩阵为单位的算法实现。因此，本文采用文献［10］中的方法计算Δθi，即

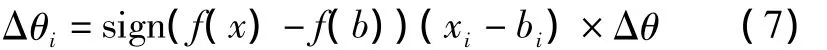
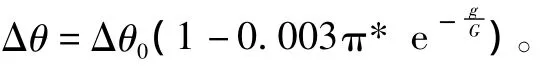
2.2 分布估计算法

分布估计算法也是一种概率种群进化方法，其主要操作算子为种群的概率估计模型，省去了遗传算法等优化算法的交叉、变异等操作，因此进化速度比较快。

标准分布估计算法的步骤为:

1)初始化种群P(t)和进化代数t=0;

2)选择优势群体构建概率估计模型ρ;

3)根据概率估计模型ρ生成新种群;

4)算法终止条件判断，如果满足终止条件，则算法结束，并保存当前的最优解，否则继续算法;

5)进化代数增加，t=t+1，转步骤2)。

可见，概率估计模型是EDA的核心，其通过概率估计模型来直接描述整个群体的进化趋势。但其是对生物进化“宏观”层面上的数学建模，对局部搜索能力较差，因此提出将EDA与量子进化算法相结合的量子分布估计算法。

2.3 基于量子分布估计算法的火力分配问题求解

1)问题编码。

在求解武器目标分配问题的各种进化算法中，可以采用以基因位表示武器所对应的目标来编码，也可以采用分配给目标的武器编号为编码，由于武器数目W一般大于目标数目T，因此采用前一种方式编码。编码时，根据武器数目W的最大值，对各武器设置二进制基因位数。

问题解的表达形式如图1所示，图中，ti表示基因位。每一个个体由长度为m的0－1编码表示，m=W*(int(lb W)+1)。

图1 问题解的个体基因表达Fig.1 Expression of the solution individual

2)适应度函数的确定。

由于费用函数变化比较平缓，其对适应值的贡献值采用幂函数形式，即 f=f′n，设 f′=C(X)(C(X)为费用函数)即n为大于1的幂函数定标参数，则

3)个体基因位的更新概率。

算法的关键是计算各基因位的更新概率。采用包含m个分量的概率向量 p(tj)=［p(t1)，p(t2)，…，p(tm)］，表示某个体 xi(i=1，2，…，n)各基因位 tj的更新概率，为了充分利用EDA的全局搜索能力及量子进化算法的局部寻优能力，考虑其中的p(tj)(j=1，2，…，m)的算式为

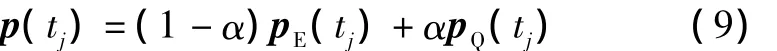
式中:pE(tj)为EDA各基因位的分布估计概率;pQ(tj)为量子进化算法中各基因位的更新概率，根据式(6)、式(7)得到;α(0＜α＜1)为调节因子。

根据上述设计，采用量子分布估计算法进行火力分配问题优化求解的步骤为:

1)初始化概率向量p(t);

2)对p(t)进行随机采样，产生n个个体;

3)计算各个体的适应值;

4)选择最好的N个个体计算种群的分布估计概率pE(tj);

5)对特定个体，产生0～1之间的随机数α，计算量子更新概率pQ(tj)，结合pE(tj)，利用式(9)进行个体更新，并保留最优个体;

6)判断终止条件是否满足，若满足，则输出优化结果;否则，转步骤2)。

3 基于量子分布估计算法的火力分配问题求解实例

对8个目标、15个火力单元的系统进行仿真，每个火力单元可单独迎击目标，其中，迎击武器的单发命中概率及目标对财产的期望损伤值随机给定，见表1及表2。分别采用分布估计算法(EDA)、量子进化算法(QEA)及量子分布估计算法(QEDA)求解武器－目标的分配，各算法均随机运行30次，统计结果见表3，最优结果的进化曲线列在图2中。

图2 QEA、EDA与QEDA的进化曲线比较Fig.2 The evolution curves of QEA，EDA and QEDA

仿真试验中，参数的设定对求解影响很大，而本文提出的量子分布估计算法的需设置参数比较少，可减小参数设置对结果的影响。取种群数n=100，最大进化代数G=100，最优个体取N=40，初始时p(t)在0～1之间随机产生。

从仿真结果的统计表2中可以看出，3种算法都收敛到了相同的最优解，各目标均有武器分配，有的目标分配的武器数目多于1个。

由图2可以看出，QEA的空间探索能力较强，EDA的全局进化能力比较好，而本文提出的量子分布估计算法由于结合了二者的优点，能充分利用进化种群的全局信息及局部信息，对解空间能够进行充分搜索，因此其优化性能很好，收敛速度最快，平均进化代数大大减少，能最大限度减小财产的损失值，并且算法的调节参数少，易于控制。

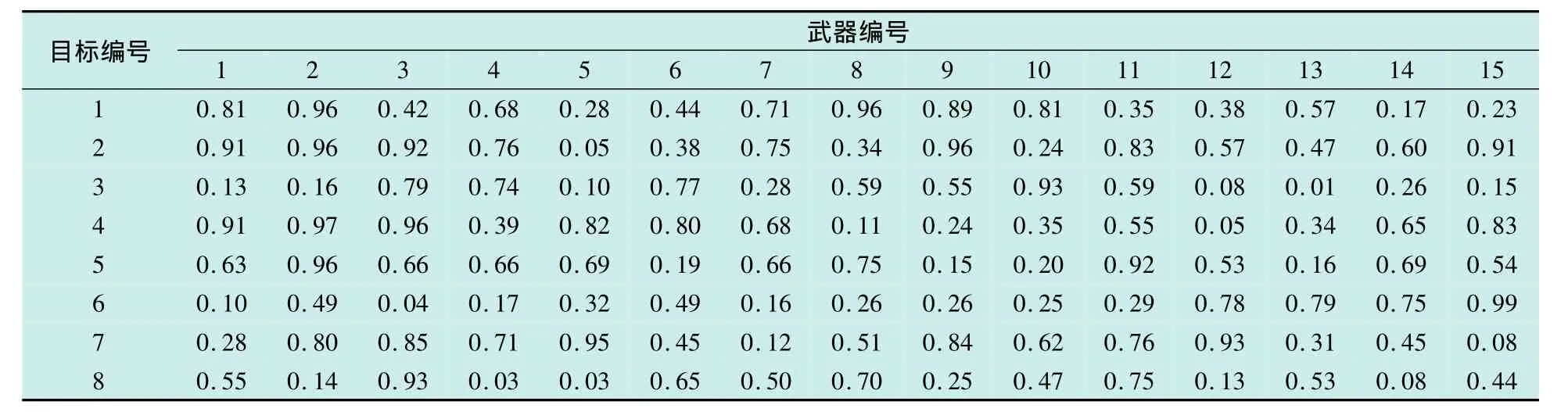
表1 武器对目标的损伤概率Table 1 Damage probability of the weapon to the target

表2 目标对财产的期望损伤值Table 2 The expected demage value of the weapon to the target

表3 武器－目标分配的仿真结果比较Table 3 Simulation results of the weapon-target assignment

4 结论

本文采用量子分布估计算法对火力分配问题进行求解，其融合了分布估计算法的较强全局搜索能力及量子进化算法适于局部寻优的特点，提高了进化效率。同时，本文采用了适合量子分布估计算法求解WTA问题的编码方案及自适应的量子进化转移算子，提高了算法的迭代效率和寻优能力，仿真结果证明了算法的有效性。本文提出的算法中需要调节的参数较少，易于控制，可应用于大规模的武器－目标实时分配，另外，也可用于其他的组合优化问题。

［1］SHIMA T，RASMUSSEN S.UAV cooperative decision and

control:Challenges and practical approaches［M］.Society for Industrial and Applied Mathematics，Philadelphia，2009.

［2］LU H Q，ZHANG H J，ZHANG X J，et al.An improved genetic algorithm for target assignment optimization of naval fleet air defense［C］//Proceedings of the 6th World Congression Intelligent Control and Automation，2006:3401－3405.

［3］高尚，杨静宇.武器—目标分配问题的粒子群优化算法［J］.系统工程与电子技术，2005，27(7):1250－1252.

［4］陈华东，王树宗，王航宇.基于混合粒子群算法的多平台多武器火力分配研究［J］.系统工程与电子技术，2008，30(5):881－883.

［5］刘建新，宋以胜，卢厚清，等.改进蚁群算法求解火力分配优化［J］.数学的实践与认识，2009，39(20):92－99.

［6］HAN K H，KIM J H.On the analysis of the quantuminspired evolutionary algorithm with a single individual［C］//2006 IEEE Congress on Evolutionary Computation，2006，7:9172－9179.

［7］王凌.量子进化算法研究进展［J］.控制与决策，2008，23(12):1321－1326.

［8］HAN K H，KIM J H.Quantum－inspired evolutionary algorithm for a class of combinatorial optimization［J］.IEEE Transactions on Evolutionary Computation，2002，6(6):580－593.

［9］PLATEL M D，SCHLIEBS S，KASABOV N.Quantuminspired evolutionary algorithm:A multimodel EDA［J］.IEEE Transactions on Evolutionary Computation，2009，13(6):1218－1232.

［10］谭立湘，郭立.基于全面学习的量子分布估计算法［J］.模式识别与人工智能，2010，23(3):314－319.