汇流环主轴刚度对测角系统精度的影响

陈 涛，施志勇

(南京电子技术研究所， 江苏 南京 210039)

汇流环主轴刚度对测角系统精度的影响

陈 涛，施志勇

(南京电子技术研究所， 江苏 南京 210039)

针对某雷达测角系统调试过程中出现轴角精度超差的现象，分析确定原因在于汇流环主轴转动扰动。应用MSC Nastran有限元软件建模，通过仿真分析研究了汇流环主轴模型在不同材料、不同形状时的扭曲变形，确定了汇流环主轴刚度不足造成轴角编码器测角精度细微偏差。对类似系统的设计具有指导意义。

汇流环；主轴；刚度；有限元分析；测角精度

引 言

雷达伺服系统中的测角系统，需要在实现跟踪的同时，完成测角的任务，实现天线实时轴角数据的高精度输出，在伺服系统中具有重要作用。测角系统的好坏，精度的高低，直接影响着伺服系统各种功能、各项指标的实现[1]。

汇流环是雷达固定部分与转动部分的电连接装置，用于大功率电源信号、中频信号和控制信号的传输。

在精密跟踪雷达系统中，常采用多极旋变与汇流环组合安装的形式。本文针对某雷达在测角系统调试过程中出现精度偏差的问题进行了有限元分析[2]，并对汇流环主轴在设计和应用中应注意的问题进行了探讨。

1 精度偏差现象描述及分析

某雷达整机联调时，测角系统调试过程中存在4′左右的测量精度误差，无法满足雷达使用要求。

影响轴角测量精度误差的因素主要包括：旋转变压器测量精度；旋转变压器的轴与机械安装轴的同轴度要求；联轴器的加工安装精度，轴系的精度和刚度；解算器件的解算精度和动态解算时的动态误差大小[3]。

该多极旋变与整机脱离，单独测试时，测量精度符合要求，由此可排除多极旋变以及解算器的因素。经分析发现，联轴器的加工安装精度或轴系的精度或刚度的不足影响了测角系统的测量精度。

常规精密测量雷达的旋变系统常安装在汇流环上方，旋变的转动通常直接由天线座主轴带动，再通过联轴节带动汇流环旋转，见图1。

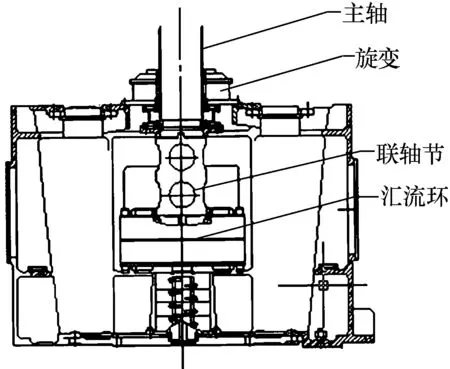
图1 旋变及汇流环安装结构图

此安装方式中旋变的转动与汇流环无直接联系，因此测量精度的误差与汇流环轴系无关。

该雷达天线座中多极旋变与汇流环的装配图见图2。

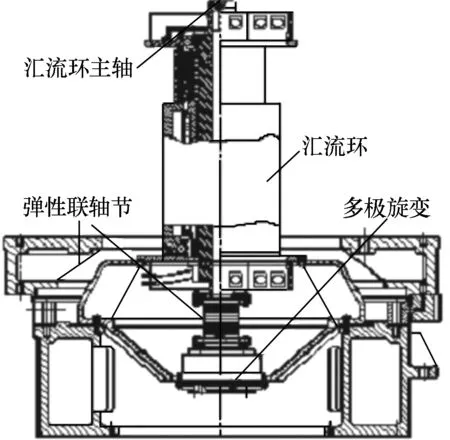
图2 汇流环与多极旋变装配图

多极旋变需由汇流环带动旋转，汇流环由控制汇流环和中频功率汇流环套装组成。控制汇流环的主轴即为汇流环主轴，转动力矩通过控制汇流环的主轴传递，再通过弹性联轴节与多极旋变的主轴相连。汇流环轴系的精度或刚度的不足就成为影响测角系统测量精度的关键因素。汇流环主轴要保证足够的刚度，防止自身的扭曲变形，才能保证测角系统精度的稳定和可靠。

控制汇流环结构见图3。

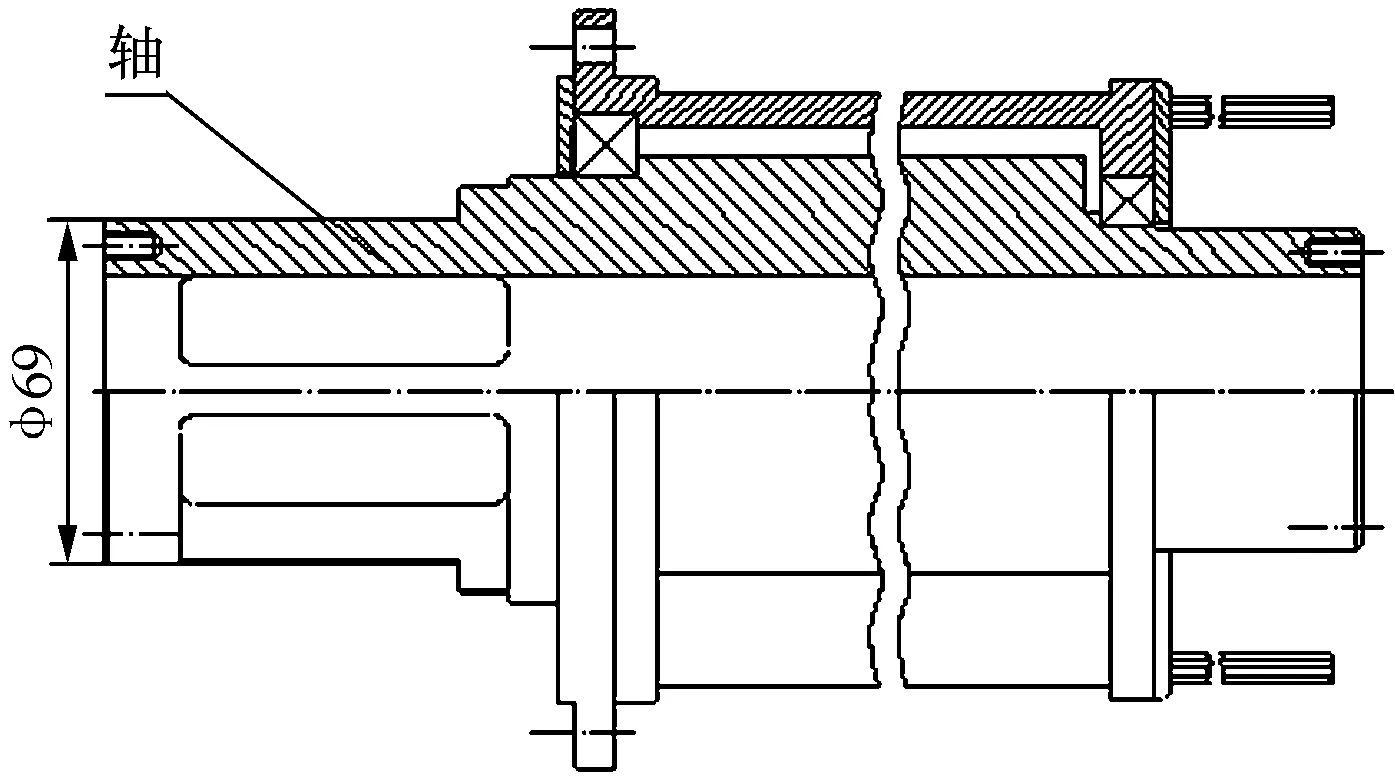
图3 控制汇流环结构示意图

为了方便控制汇流环出线，在轴的左端开了4个长65 mm的出线孔，在此部位只留有4根支撑筋，因此整个轴上此部位刚度最差。

根据实测，汇流环自身转动力矩为7 N·m，轴角编码器转动力矩不大于2 N·m。在安装到天线座上之后，考虑到汇流环与旋变之间可能存在转轴不同心现象，转动一周过程中个别角度的转动力矩可能会有所增大，因此汇流环带动旋变转动的最大转动力矩约为10 N·m。本文通过有限元数值模拟的方法，对该主轴结构进行了仿真分析。

2 仿真计算

汇流环主轴为铝质材料，外形尺寸：外径63 mm；内径45 mm；长804 mm。

采用Pro/E对汇流环主轴进行建模，分析时采用MSC Nastran通用有限元软件，有限元模型采用实体单元建模，共产生36 142个节点和124 631个单元。

模型材料参数为：弹性模量E=0.7×105MPa；泊松比μ=0.3；质量密度ρ=2.7×103kg/m3。

边界条件定义：主轴一端采用固定端约束；另一端施加一10 N·m力矩，通过一个刚性单元均匀分布在主轴端面上。有限元模型如图4所示。

图4 汇流环主轴有限元模型

有限元仿真结果表明，汇流环主轴在10 N·m扭矩的作用下，扭转刚度较弱的左端相对于右端的扭转变形位移为4.47×10-2mm。汇流环主轴左端直径为69 mm。相对转角：

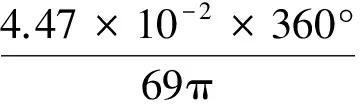
主轴变形云图如图5所示。

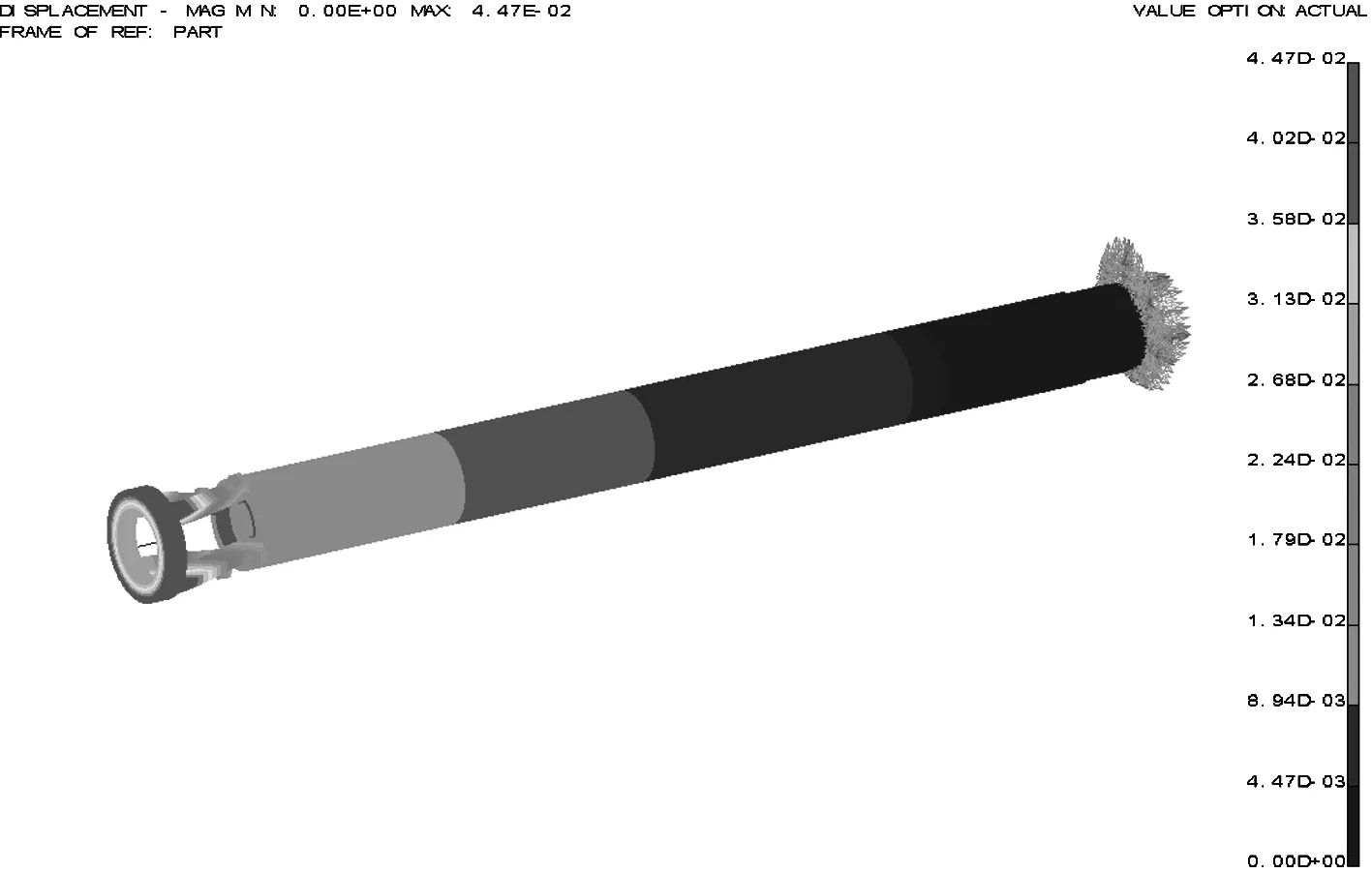
图5 汇流环主轴变形云图

汇流环主轴应力和变形主要集中在主轴左端刚度最弱处。主轴4.45′的转角变形与轴角编码器4′的测量误差基本一致，因此正是由于此处控制汇流环主轴的扭转刚度较低，从而造成转动过程中的扰动现象，影响了测角系统的测量精度。

3 改进措施

铝质材料的扭转刚度较低，为加强控制汇流环主轴的扭转刚度，在主轴中套一加固轴。加固轴外形见图6，外径44 mm，内径26 mm，材料为45号圆钢。

图6 加固轴外形图

汇流环加装加固轴后的结构示意图见图7。

图7 汇流环加装加固轴后的结构图

对改进后的主轴结构进行有限元分析。同样采用Pro/E建模，采用MSC Nastran分析，有限元模型如图8所示。

图8 改进后主轴有限元模型

模型材料参数为：弹性模量E=2.06×105MPa；泊松比μ=0.3；质量密度ρ=7.8×103kg/m3。

有限元仿真结果表明，改进后主轴在10 N·m扭矩的作用下，扭转变形为8.15×10-3mm。相对转角：

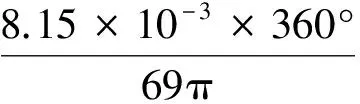
主轴变形云图如图9所示。

图9 改进后主轴变形云图

加装加固轴之后控制汇流环主轴的刚度得到增强，其抗扭转变形能力明显提高。

改进后雷达测角系统的测量精度误差由原来的4′降到了0.7′，满足雷达伺服系统使用要求。

4 结束语

该雷达汇流环主轴经过安装加固轴的改进措施后，有效解决了测角系统的测量精度偏差问题。后期产品中将原主轴材料改成45号圆钢，外形设计时改变汇流环走线方式，主轴上不开设窗口，汇流环主轴自身刚度得到加强。

雷达系统中，天线座主轴的刚度可设计得较强，汇流环主轴受其自身结构限制，刚度性能要较天线座主轴差。当雷达系统中汇流环与旋变两个分系统同时存在时，要尽可能将旋变安装在汇流环上端，旋变的转动直接由天线座主轴带动，避免与汇流环之间存在连带转动关系。若受天线座结构限制，旋变系统只能安装在汇流环下方，旋变的转动由汇流环带动，则汇流环主轴必须具有足够的扭转刚度。要尽量避免在主轴上开设窗口，主轴材料尽可能选用刚度、强度高的材料。

[1] 李素梅. 雷达天线轴角编码器实现的一种新方法[J]. 无线电通信技术, 1999, 25(4): 24-25.

[2] 魏忠良, 陈玉振, 岳振兴. 传动齿轮疲劳寿命的仿真分析[J]. 电子机械工程, 2010, 26(6): 56-58, 61.

[3] 高建华. 轴角编码器误差分析及控制[J]. 零八一科技, 2001(2): 46-49.

陈 涛(1977-)，男，工程师，主要从事汇流环设计工作。

施志勇(1978-)，男，高级工程师，主要从事天线座设计工作。

Effect of the Rigidity of Collector Ring Spindle on the Accuracy of Angle Measurement System

CHEN Tao，SHI Zhi-yong

(NanjingResearchInstituteofElectronicsTechnology，Nanjing210039,China)

The angle measurement accuracy deviation has occurred in the adjustment of a radar angle measurement system. It is confirmed that this deviation is resulted from the disturbance of the turning collector ring spindle. The problem is modeled using the finite element analysis software MSC Nastran. Model twist and de-formation of the collector ring spindle with different materials and different shapes are studied. Simulation analysis result confirms that the reason of the slight angle measurement accuracy deviation of the axial angle coder is that the collector ring spindle is not rigid enough. Results of this paper have guidance value for similar design.

collector ring; spindle; rigidity; finite element analysis; angle measurement accuracy

2013-04-18

TH114；TH115；TN820.3

A

1008-5300(2013)04-0028-03