遥感图像几何精纠正中更为有效的稳健估计方法

丁 娟，葛永慧

（太原理工大学 矿业工程学院测绘科学与技术系，太原030024）

遥感图像在投入使用前，需要对图像中产生的畸变进行几何纠正。遥感图像几何纠正的方法有多项式纠正法、共线方程纠正法、空间投影法等［1］。多项式纠正法原理直观、计算简单，适用于地面平坦地区；共线方程纠正法引用了地面高程信息，在地形起伏较大的地区，纠正精度要高于多项式纠正法［2］；空间投影法精确地模拟了卫星动态成像的几何关系，它只需少量地面控制点，就能直接建立影像与投影之间、像点与地面点之间严格的数学关系［1］。几何纠正，即图像级别中的几何精纠正，主要方法是多项式纠正法［3］。

多项式纠正法通常用最小二乘（LS）估计求取转换参数。但是当观测值中不可避免地含有粗差时，LS估计也会受到很大的干扰［4］，结果便会受到歪曲。G．E．P．BOX提出的稳健估计的概念［5］，可以消除或减弱粗差对参数估计的影响，然而不同稳健估计方法减弱和消除粗差对参数估计影响的能力不同。Li［6］认为Fair法的效果要优于残差绝对和最小法（L1法），而Danish法的计算量相对其他方法较大。Sharmishtha Mitra等［7］的研究表明，由于重尾噪声分布的存在，Andrews法和Huber法的稳健性要优于残差绝对和最小法。Pennacchi［8］用算例证明，迭代100次以后，Cauchcy法比 Welsch法、German－McClure法和Tukey法的效果都要好。焦伟利等［5］提出利用稳健理论自动检测和消除图像校正中的控制点粗差，实验结果表明，稳健估计可以有效消除观测值中的粗差，使验后单位权方差变小，同时提高控制点的拟合精度。那么，多项式纠正法在求取转换参数时，哪些稳健估计方法相对更为有效呢？

笔者采用多项式纠正法建立模型，通过仿真实验（1 000次）对不同的观测值数量、粗差数量和粗差数值的13种稳健估计方法消除或减弱粗差的能力进行了比较，确定了遥感图像几何精纠正中相对更为有效的稳健估计方法。

1 材料与方法

1．1 13种常用的稳健估计方法及其权函数

13种常用的稳健估计方法如下。在下列各式中，u代表标准化的残差指标表示权函数；a，b和c表示调和系数，它们的值均采用有关文献的推荐值。

1）Huber法［9］：

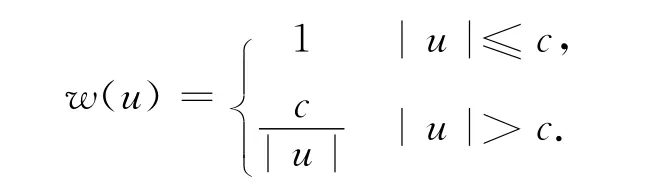
式中：c＝1．5．

2）L1法（残差绝对和最小法）［8］：

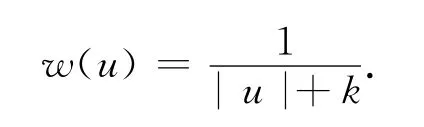
式中：k为很小的数。

3）L1－L2法［8］：

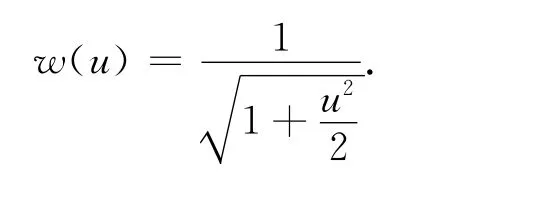
4）Andrews法［10］：

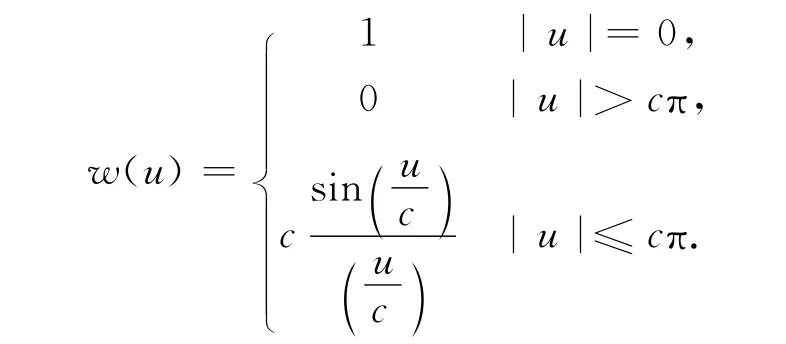
式中：c＝1．339．

5）Hampel法［11］：

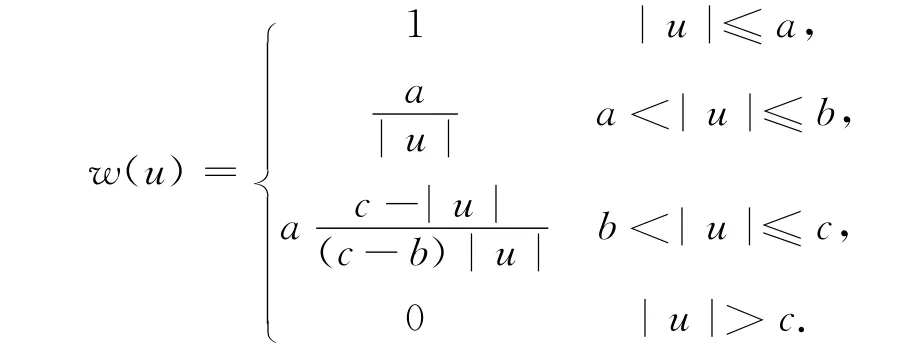
式中：a＝1．6；b＝3；c＝6．5．

6）Welsch法［8］：

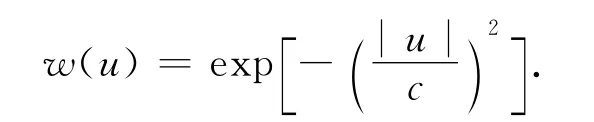
式中：c＝2．984 6．

7）Tukey法［8］：

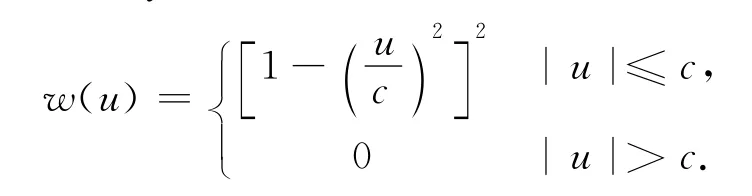
式中：c＝4．685 1．

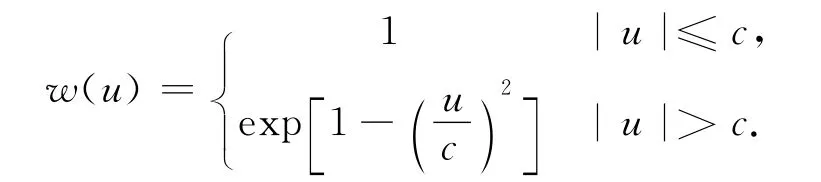
8）Danish法［12－13］：式中：c＝1．5或c＝1．4，在本文中，c＝1．5．

9）Fair法［8］：

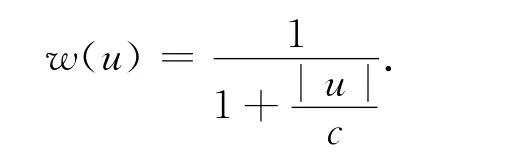
式中：c＝1．399 8．

10）German－McClure法［8］：

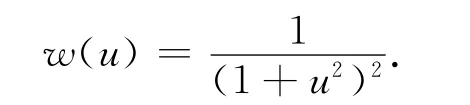
11）IGG 方案［13－14］：

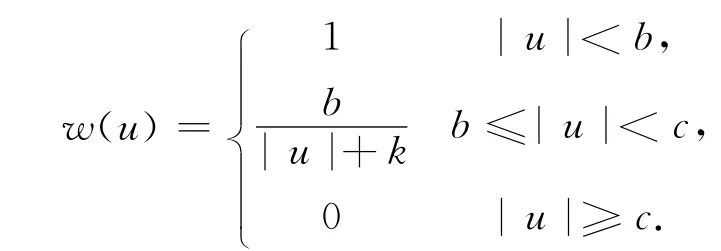
式中：b＝1．5；c＝2．5；k为很小的数。

12）IGGⅢ方案［15－16］：

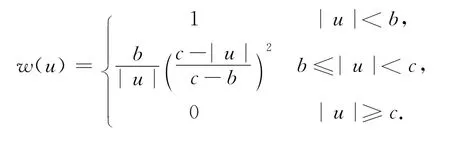
式中：b＝1．0～1．5；c＝2．5～3．0．在本文中，b＝1．5，c＝3．0．

13）Cauchy法［8］：

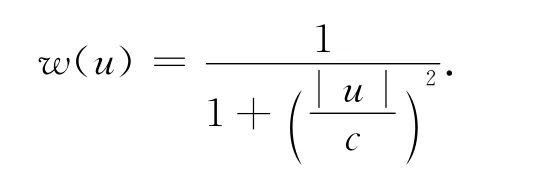
式中：c＝2．384 9．

1．2 两种稳健估计方法比较指标

1．2．1 残余真误差均方误差与相对增益

文献［17］提出了残余真误差均方误差和相对增益两种指标，用仿真实验的方法比较了任意两种参数估计。笔者采用文献［17］提出的方法比较13种稳健估计方法对于遥感图像精纠正消除或减弱粗差的能力。

两种稳健估计方法比较的绝对指标——残余真误差均方误差（＾σf）：

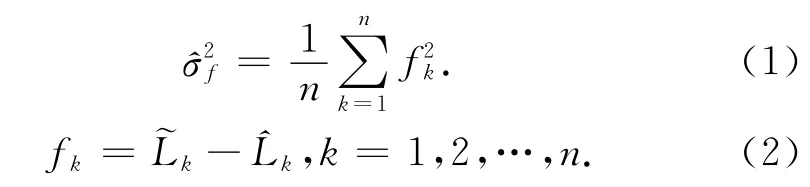
式中：fk为残余真误差为观测值Lk的真值为通过参数估计方法得到观测值Lk的估值，并随着参数估计方法的不同而不同；n为观测值的数量。

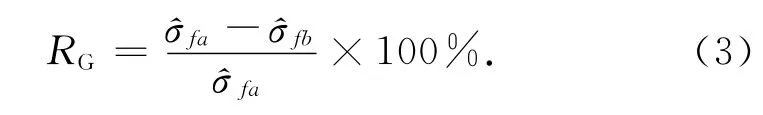
两种稳健估计方法比较的相对指标——相对增益（RG）：式中和为A 和B 两种参数估计方法对于同一个参数估计问题1 000次仿真实验残余真误差均方误差的平均值。当RG＞0时，B方法相对于A方法的相对增益提高；当RG＝0（或接近0）时，B方法与A方法参数估计结果等价；当RG＜0时，B方法相对于A方法的相对增益降低。因此，RG从实质上可以说明两种参数估计方法哪个更有效。在本文中，各种稳健估计方法相对于LS法的相对增益简称为相对增益。

1．2．2 观测值中包含粗差的仿真实验

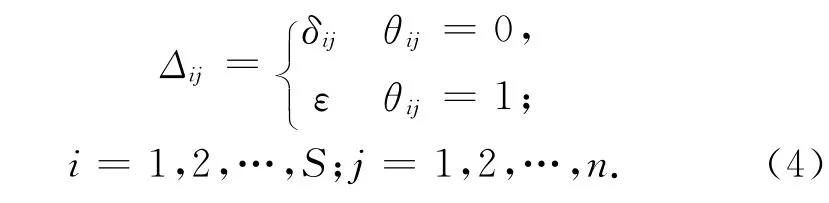
用观测值的真值减去包含粗差的随机误差得到S组包含粗差的模拟观测值：

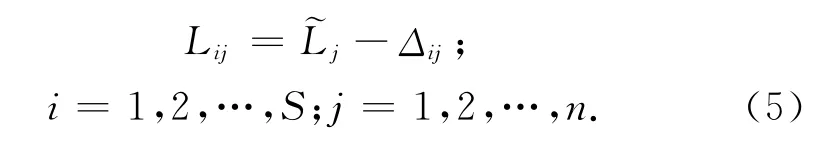
用各种稳健估计方法和最小二乘法分别计算S组中每一组模拟观测值的MSRTE，并取它们的平均值作为观测值中包含g个粗差ε时此方法的MSRTE。稳健估计方法的终止条件是相邻两次残差之差的绝对值的最大值小于0．1像素。用最小二乘法和不同稳健估计方法得到的MSRTE分别计算每一种稳健估计方法相对于最小二乘法的增益。

1．3 遥感图像几何精纠正模型

遥感图像几何精纠正的主要方法是多项式纠正法，其建立了控制点像坐标（x，y）与其控制点地面空间坐标（u，v）之间的关系，多项式纠正模型的数学表达式［18］为：

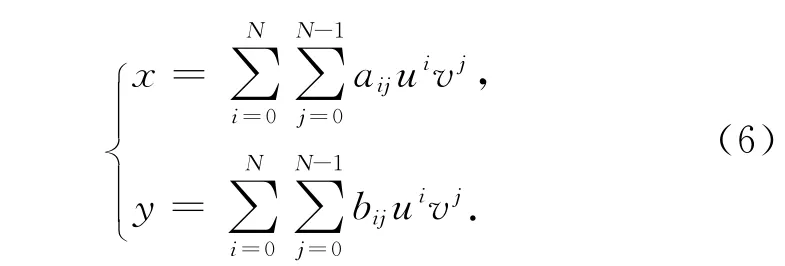
式中：aij、bij为多项式系数；N 是多项式次数，取决于图像变形的程度和地面控制点的数量，建立N次多项式模型所需控制点数至少要（N＋1）×（N＋2）／2个。一般情况采用二次多项式，表达为：

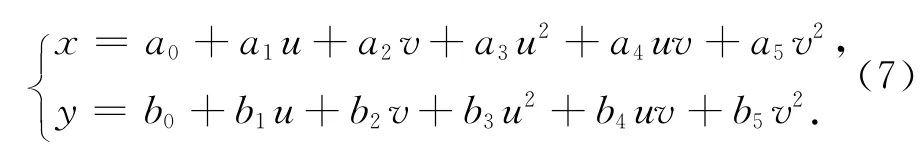
式中，x、y的表达式具有相同的形式。在本研究的仿真实验中，以x为例，计算坐标转换参数a0，a1，a2，a3，a4，a5。仿真实验中的重合点如图1所示，重合点的坐标真值是模拟值，9～15个重合点的选取方式如下：

9个重合点：P11，P13，P15，P31，P33，P35，P51，P53，P55；

10个重合点：P11，P13，P15，P31，P32，P34，P35，P51，P53，P55；

11个重合点：P11，P12，P14，P15，P31，P33，P35，P51，P52，P54，P55；

12个重合点：P11，P12，P14，P15，P31，P32，P34，P35，P51，P52，P54，P55；

13个重合点：P11，P13，P15，P22，P24，P31，P33，P35，P42，P44，P51，P53，P55；

14个重合点：P11，P13，P15，P22，P23，P24，P31，P35，P42，P43，P44，P51，P53，P55；

15个重合点：P11，P13，P15，P22，P23，P24，P31，P33，P35，P42，P43，P44，P51，P53，P55．

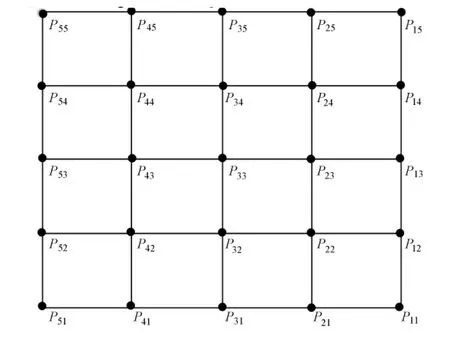
图1 重合点分布图

2 结果与讨论

2．1 遥感图像几何精纠正仿真实验

当观测值数量n＝9，粗差数量g＝1时，取粗差ε＝5．0σ0进行1 000次的仿真实验，分别计算LS法和13种稳健估计方法的残余真误差均方误差，并取它们的平均值作为相应的残余真误差均方误差（见表1）。对于粗差ε＝10．0σ0作同样的计算。相应地，计算出13种稳健估计方法相对于LS法的相对增益（见表2）。

表1 不同稳健估计方法的残余真误差均方误差（n＝9，g＝1） 像素

在后续的仿真实验中，分别计算在n（9～15）个观测值中含有g（1～3）个粗差、ε为5．0σ0和10．0σ0时，LS法和13种稳健估计方法的残余真误差均方误差，并分别计算出相对应的13种稳健估计方法相对于LS法的相对增益。

表1中，MLS表示LS法得到的残余真误差均方误差；M1，M2，M3，M4，M5，M6，M7，M8，M9，M10，M11，M12，M13分别表示 Huber法、L1法、L1－L2法、Andrews法、Hampel法、Welsch法、Tukey 法、Danish法、Fair法、German－McClure法、IGG 方案、IGGIII方案、Cauchy法得到的残余真误差均方误差。

表2 不同稳健估计方法的相对增益（n＝9，g＝1） %

表2中，R1，R2，R3，R4，R5，R6，R7，R8，R9，R10，R11，R12，R13分别表示 Huber法、L1法、L1－L2法、Andrews法、Hampel法、Welsch法、Tukey法、Danish法、Fair法、German－McClure法、IGG方案、IGGIII方案、Cauchy法相当于LS法的相对增益。

2．2 仿真实验结果与讨论

图2是当n＝9～15并且g＝1，n＝13～15并且g＝2，n＝15并且g＝3时，13种常用稳健估计方法相对于LS法的相对增益的平均值。

由图2可知，L1法（R2）和 German－McClure法（R10）是相对更为有效的稳健估计方法。当粗差ε＝5．0σ0时，L1法和 German－McClure法的相对增益平均值分别是13%和11%，其他稳健估计方法的相对增益平均值均小于等于10%。当粗差ε＝10．0σ0时，L1法和German－McClure法的相对增益平均值分别是39%和38%，其他稳健估计方法的相对增益平均值均小于等于24%。

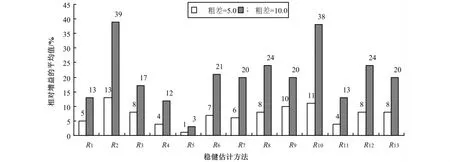
图2 不同稳健估计方法相对于LS法的平均相对增益

3 结论

笔者通过仿真实验（1 000次），对不同的重合点（观测值）数量（9～15个）、粗差数量（1～3个）和粗差数值（5．0σ0、10．0σ0）的13种稳健估计方法消除或减弱粗差的能力进行了比较。仿真实验结果说明，13种常用稳健估计方法都有消除或减弱粗差影响的能力，但是能力大小不尽相同。总体上，对于遥感图像几何精纠正，L1法和German－McClure法是相对更为有效的稳健估计方法，它们比其他常用稳健估计方法能更有效地消除或减弱粗差的影响。

［1］ 程志梅，陆玲，邱霞明．利用空间投影法实现遥感图像的几何精纠正［J］．科技广场，2005（10）：103－105．

［2］ 刘云峰，李若．不同 DEM 数据对卫星遥感影像纠正精度的影响［J］．测绘通报，2002（7）：26－28．

［3］ 王学平．遥感图像几何校正原理及效果分析［J］．计算机应用与软件，2008，25（9）：102－105．

［4］ 归庆明，张建军，郭建锋．压缩型抗差估计［J］．测绘工程，2000，29（3）：224－228．

［5］ 焦伟利，何国金，王威，等．稳健估计方法求解遥感图像几何校正模型研究［D］．北京：中国科学院对地观测与数字地球科学中心，2009．

［6］ Huifen Li，Xaingqian Jiang，Zhu Li．Robust estimation in Gaussian filtering for engineering surface characterization［J］．Precision Engineering，2004（28）：186－193．

［7］ Sharmishtha Mitra，Amit Mitra，Debasis Kundu．Genetic algorithm and M－estimator based robust sequential estimation of parameters of nonlinear sinusoidal signals［J］．Communications in Nonlinear Science and Numencal Simulation，2011，16（7）：2796－2809．

［8］ Pennacchi P．Robust Estimate of Excitations in Mechanical Systems Using M－estimators—Theoretical Background and Numerical Applications［J］．Journal of Sound and Vibration，2008，310（4－5）：923－946．

［9］ Baselga S．Global Optimization Solution of Robust Estimation［J］．Journal of Surveying Engineering，2007，133（3）：123－128．

［10］ El－Hawary F，Mbamalu G A N．Fair and Andrews＇s weighting－based IRWLS algorithms for time－delay estimation in underwater target tracking［J］．Ieee Journal of Oceanic Engineering，1993，18（2）：142－150．

［11］ 李浩军，唐诗华，黄杰．抗差估计中几种选权迭代法常数选取的探讨［J］．测绘科学，2006，31（6）：70－72．

［12］ Knight L，Wang J L．A Comparison of Outlier Detection Procedures and Robust Estimation Methods in GPS Positioning［J］．Journal of Navigation，2009，62（4）：699－709．

［13］ 王新洲，陶本藻，邱卫宁．高等测量平差［M］．北京：测绘出版社，2006．

［14］ 周江文．经典误差理论与抗差估计［J］．测绘学报，1989，18（2）：115－120．

［15］ 常志巧，郝金明，张成军，等．GPS快速定位中病态问题的正则化抗差解法［J］．大地测量与地球动力学，2008，28（3）：83－86．

［16］ 文援兰，杨元喜，王威．卫星精密轨道抗差估计的研究［J］．空间科学学报，2001，21（4）：341－350．

［17］ Ningning Jia，Yonghui Ge．Remainder reliability and robust estimation：A case study using twelve simulated leveling networks，2013（263－266）：3163－3167．

［18］ 黄世存，章文毅，何国金，等．几种不同矩阵算法的遥感图像几何精纠正效果比较［J］．国土资源遥感，2005（3）：18－22，43．