基于白光干涉泥岩表面形貌试验研究
韩文梅,康天合
(1.中北大学 理学院,太原030051;2.太原理工大学 采矿工艺研究所,太原030024)
岩石的摩擦滑动性质对于断裂岩体的稳定性有着重要的影响,而影响岩石摩擦滑动性质的一个主要因素就是岩石滑动面的表面形貌[1,2]。在试验研究岩石摩擦滑动性质的过程中,岩石摩擦滑动面主要为自然断裂面、锯开面和抛光面等三种,其中,自然断裂面可以很好地反映出岩石自然断裂的特征,但摩擦滑动过程中岩石滑动面的几何性质不易确定;锯开面和抛光面可以很好地反映出摩擦滑动过程中岩石滑动面的几何性质,即滑动面的表面形貌,在一定程度上,锯开面也是抛光面的一种,因此,岩石抛光表面形貌的研究对于岩石的摩擦滑动性质有重要的影响。
表面形貌的测量方法主要为接触式测量法和非接触式测量法,各有优缺点和应用范围[3-5]。非接触测量法主要分为非光学式扫描显微镜测量法和光学测量法,白光干涉作为光学测量法中的一种,具有灵敏度高、稳定性高和抗干扰性强等优点[3,6],可以获得岩石抛光表面形貌的所有数据,成为近些年来国内外的研究重点。
已有的岩石表面形貌表征方法[7,8]主要为统计学参数表征和分形几何表征等两种方法。在统计学方法中,岩石表面形貌表征的核心内容是岩石表面粗糙度,采用中线制得到岩石表面的轮廓算术平均中线,根据该中线从岩石表面微观不平度高度、间距和形状等方面对岩石的表面形貌进行量化描述,得到轮廓算术平均偏差、轮廓均方根偏差、粗糙度参数平均值、轮廓最大谷深和轮廓最大峰高等一系列粗糙度参数。在分形几何学方法中,当岩石的抛光表面形貌具有分形特征时,其测度和尺度的双对数曲线为直线,分形维数为描述岩石抛光表面形貌的唯一参数,不依赖于测量仪器的分辨率和取样尺度,可以通过某一尺度的测量来表征表面形貌在所有尺度下的特性,是表征表面形貌的固有参数。本文采用白光干涉显微镜法对泥岩样抛光表面形貌进行测定,在此基础上,采用统计学和分形几何方法对泥岩样表面形貌进行进一步表征。
1 试验岩样及装置
1.1 试验岩样
试验所用泥岩样为山西高平唐安煤矿3410工作面回风顺槽距四盘区轨道运输巷300m处的顶板泥岩,属二叠系下统山西组,为陆相碎屑沉积岩。
1.2 试验装置
采用岩石切割机将该泥岩样加工成50mm×50mm×50mm的试验岩样。选择一个面,采用岩石抛光机进行表面抛光,抛光机型号为SIP-MSD-180,功率为760W,转速为4 000r/min,抛光片为500号聚氨酯片。
试验岩样抛光表面形貌测定仪器为American MicroXAMTMADE三维白光干涉表面形貌仪。该仪器的XYZ三轴行程为100mm×100mm×100 mm,垂直扫描范围为30μm~100mm,分辨率为480×752像素,垂直扫描分辨率最小可到0.01 nm,侧向分辨率最小可到8.8nm~0.01μm,重复精度为1nm,校正精度≤0.1%,视场范围为84μm×63μm~8mm×10mm,放大倍数为2.5倍、10倍和50倍。
对试验岩样抛光表面形貌进行测定,测试面积为857μm×638μm,空间采样为1.1μm×1.3μm,光学分辨率为0.92μm,工作距离为7.4mm,聚焦深度为3.89μm,放大倍数为10倍。
2 表面形貌分析方法
2.1 表面形貌统计学表征
统计学表征表面形貌的主要内容是表面粗糙度,表征方法为中线制,根据测定的泥岩样抛光表面形貌,得到表面形貌的轮廓算术平均中线,基于该中线通过计算得到表面形貌统计学参数。
选择具有代表性的轮廓算术平均偏差Ra、轮廓均方根偏差Rq、粗糙度参数平均值R、轮廓最大谷深Rm和轮廓最大峰高Rp等5个粗糙度参数作为试验岩样表面形貌统计学参数。其计算公式为
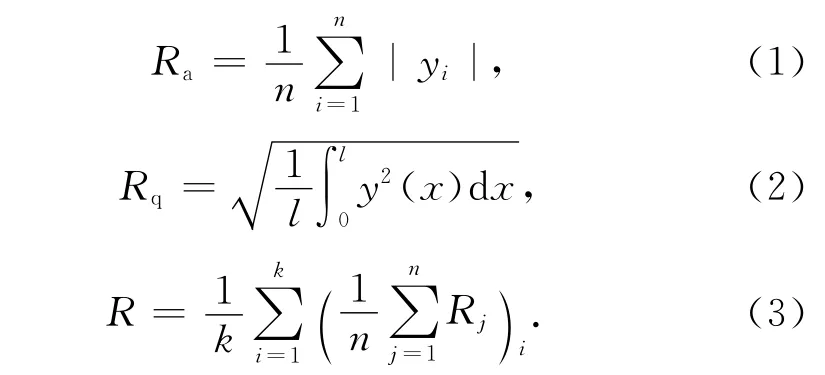
式中:l为取样长度;k为评定长度的个数;Rm为取样长度内从轮廓谷底线至中线的距离;Rp为取样长度内从轮廓峰顶线至中线的距离。
2.2 表面形貌分形几何表征
2.2.1 功率谱法
根据 Majumdar[9]所推导的W-M 函数
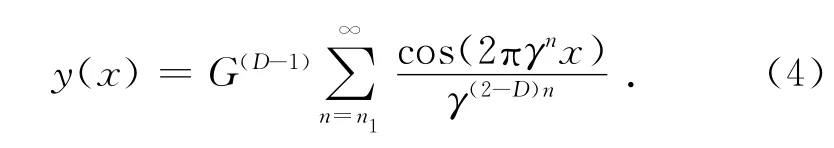
式中:x为采样长度;y为轮廓高度;G为表面特征长度尺度系数;D为分形维数,1<D<2;γn为空间频率的模,为滑动面表面波长的倒数,即
对式(1~4)进行快速傅立叶变换,得其功率谱函数S(ω)
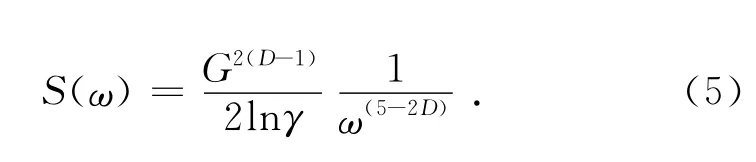
式中:ω为空间频率。
对式(1~5)取对数,得分形维数功率谱法的计算公式
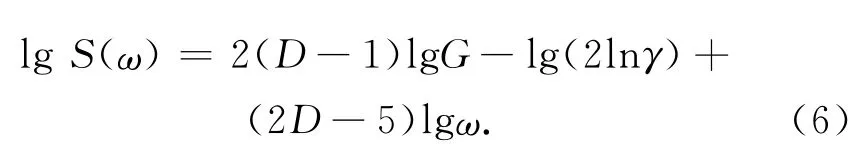
2.2.2 盒维数法
根据测度位数的定义,滑动面表面的分形维数D 为[10]
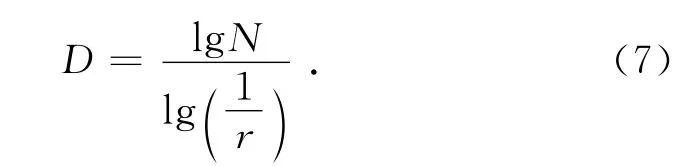
式中:N为盒子r量度表面的结果。对于M×M的图像,用单位为e的网格划分整个图像,则N对式(1~7)取对数,得分形维数盒维数法的计算公式
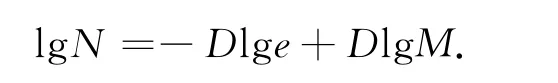
2.2.3 三角测量法
三角测量法是将表面形貌二维图像看作类似数字正视模式(Digital Elevation Model)的三维矩阵,将图像上每一像素的灰度值作为z值,将二维图像转化到三维图像。图像柵格的4个角,即a、b、c、d,组成图像的面积作为正视图的值。取这4个点的中心线交点作为中心点e点,四个三角形abe、bce、cde和dae的表面积之和即为a、b、c、d所组成的图像的表面积,即图像栅格的表面积。随着栅格尺度L的变化,重复计算,即可得到图像栅格的表面积与栅格尺度之间的关系
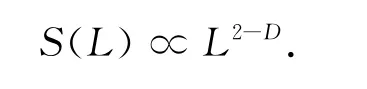
式中:S(L)为图像的表面积;L为栅格尺度。对其取对数得
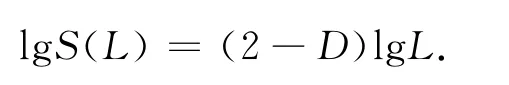
式中:(2-D)为该双对数曲线的斜率。
由上述分析可知,功率谱法是基于轮廓算术平均中线计算一维分形集的分形维数;盒维数法和三角测量法是基于表面图像计算二维分形集的分形维数,其关系为二维分形集的分形维数为一维分形集的分形维数加1[10-11]。
3 试验结果及分析
3.1 试验结果
图1为采用白光干涉法测得的试验岩样表面形貌二维图像。
从图1中可以看出,试验岩样表面抛光后,岩样表面仍呈现为凹凸不平。在该岩样抛光表面形貌中,含有大量的微凸体,该微凸体是由泥岩样表面的岩石颗粒所组成,白色光亮部分为山峰形状的微凸体,颜色较暗的为山谷形状的微凸体,这两种形状的微凸体呈不规律状,且数量繁多,表现为无序性、自相似性、自仿射性和多尺度等性质,具有分形特征。

图1 试验岩样表面形貌二维图像
3.2 试验结果分析
对图1所示的试验岩样表面形貌二维图像进行进一步分析,图2为试验样抛光表面的表面轮廓算术平均中线。
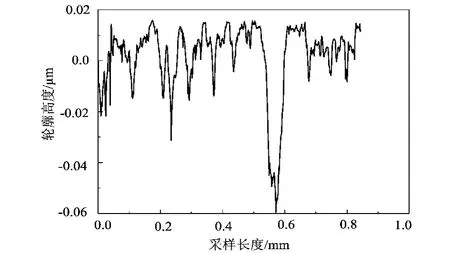
图2 试验岩样表面轮廓算术平均中线
从图2中可以看出,在轮廓高度为-0.06~0.02μm范围内,试验岩样表面轮廓高度成无序性和自相似性。基于该表面轮廓算术平均中线,采用统计学方法根据式(1)~(3)表征试验岩样的轮廓算术平均偏差Ra、轮廓均方根偏差Rq、粗糙度参数平均值R、轮廓最大谷深Rm和轮廓最大峰高Rp等5个粗糙度参数,其计算结果分别为0.28,0.4,0.71,13.55,2.24μm。由该计算结果可知,轮廓算术平均偏差Ra、轮廓均方根偏差Rq和粗糙度参数平均值R这三个粗糙度参数值相接近,为0.28,0.4,0.71μm;轮廓最大谷深Rm和轮廓最大峰高Rp这两个参数值相差较大,分别为13.55μm,2.24μm。这一结果说明,对试验岩样滑动面进行抛光,影响的是Ra、Rq和R这三个粗糙度参数,对Rm和Rp这两个粗糙度参数的影响不大,其原因为试验岩样抛光后,抛光表面仍存在大量的微凸体,相对于表面轮廓算术平均中线,Rm和Rp使得该中线呈现无序性,Ra、Rq和R使得该中线在一定范围内发生变化。
这5个粗糙度参数是以欧氏几何为基础,从试验岩样抛光表面微观不平度高度等方面对试验岩样抛光表面形貌进行了量化描述,对岩石摩擦滑动微观机理的研究具有积极的意义,但也存在一些不足之处。采用统计学方法表征试验岩样抛光表面粗糙度是基于表面轮廓算术平均中线,即这些粗糙度参数是在一定的测量条件下得到的统计学表征参数,只能表征试验岩样表面形貌二维图像的局部表面形貌,不能表征整体表面形貌,且这些粗糙度参数所表征的表面形貌特征不具有唯一性。
图3为采用功率谱法得到的试验岩样表面轮廓功率谱,对其进行线性拟合,拟合的线性方程为
lgS(w)=43.68-2.03lgw.
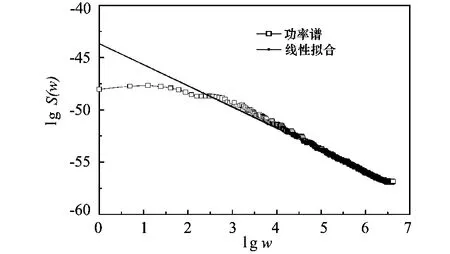
图3 试验岩样功率谱法双对数曲线
从图3可以看出,lgω在2.31~6.62范围内,lgS(ω)与lgω为直线线性关系,表明试验岩样抛光面轮廓在该范围内具有分形特性,分形维数D为1.49。
图4为采用盒维数法得到的试验岩样抛光表面
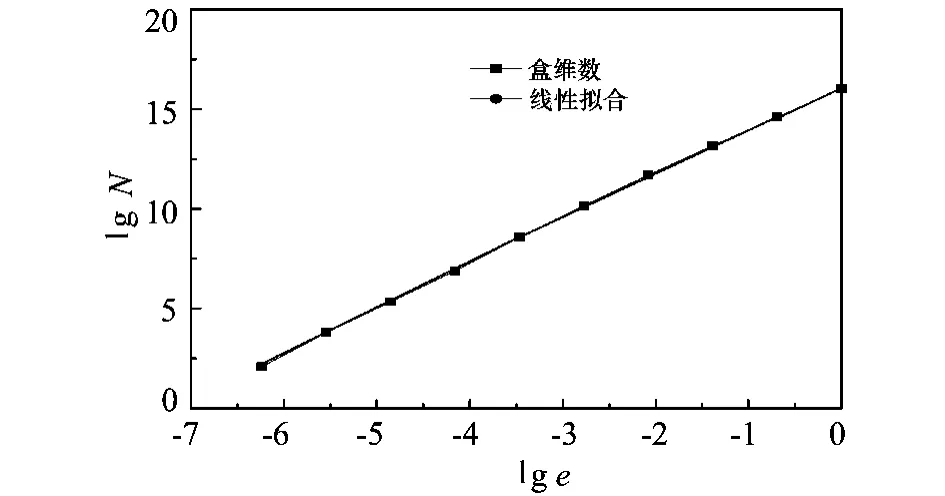
图4 试验岩样盒维数法双对数曲线
双对数曲线,对其进行线性拟合,拟合的线性方程为
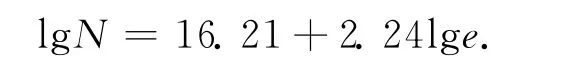
从图4可以看出,lge在-6.24~0范围内,lgN与lge为直线线性关系,表明试验岩样抛光表面在该范围内具有分形特性,分形维数D为2.24。
图5为采用三角测量法得到的试验岩样抛光表面双对数曲线,对其进行线性拟合,拟合的线性方程为
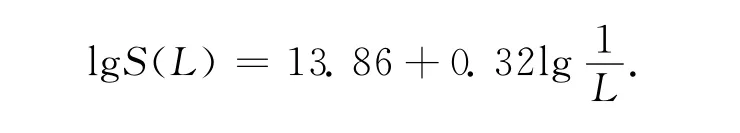
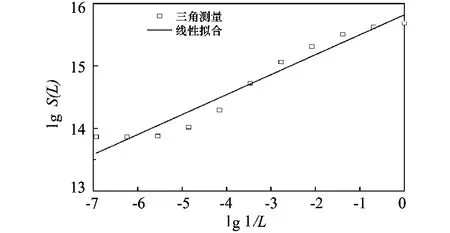
图5 试验岩样三角测量法双对数曲线
分形参数是岩石表面形貌的固有参数,不依赖于仪器的分辨率和取样长度。功率谱法、盒维数法和三角测量法的分形维数不相一致,其原因主要是三者的算法不同。从三者的算法上可以看出,功率谱法是基于轮廓算术平均中线,对轮廓算术平均中线进行FFT变换,得到轮廓的功率谱函数,功率谱函数将离散高度转换成频率来计算,会产生许多近似误差;盒维数法和三角测量法基于滑动面表面形貌图像实现其算法,图像像素的大小和灰度级数会对分形维数的计算结果产生误差。已有的成果表明[12-18],相对于理论分形维数,功率谱法的计算结果远大于理论分形维数,尤其是当分形维数较小时[18];盒维数法的计算结果偏小[18],偏差约为4%~10%[12];三角测量法的计算结果偏差最小[13,18],偏差约为1%~3%[15,16]。从图3~图5的计算结果中也可以看出,功率谱法的计算结果最大,三角测量法的计算结果次之,盒维数法的计算结果最小,综合这三种计算方法,取三角测量法的分形维数计算结果作为本试验岩样抛光表面形貌的分形维数。
4 结论
1)基于白光干涉法对泥岩抛光表面形貌进行了试验研究,从白光干涉法得到的泥岩抛光表面形貌二维图像中可以看出,泥岩样被抛光后,抛光表面呈现为凹凸不平,存在大量微凸体,其中,白色光亮部分为山峰形状的微凸体,颜色较暗的为山谷形状的微凸体,这两种形状的微凸体呈不规律状,数量繁多,表现为无序性、自相似性、自仿射性和多尺度等性质。
2)采用统计学方法从微观不平度高度等方面对泥岩抛光表面形貌进行了量化表征,表征参数为轮廓算术平均偏差Ra、轮廓均方根偏差Rq、粗糙度参数平均值R、轮廓最大谷深Rm和轮廓最大峰高Rp等5个粗糙度参数,这些参数可以表征泥岩抛光表面形貌的局部区域,不能表征表面整体区域的形貌,且用这些粗糙度参数所表征的表面形貌特征值不具有唯一性。
3)采用分形几何法对泥岩抛光表面形貌进行了量化表征,表征参数为分形维数,分形维数具有唯一性,是表征泥岩抛光表面形貌的固有参数。
4)通过对泥岩抛光表面形貌的试验研究,结果表明,统计学方法得到的粗糙度参数反映的是泥岩抛光表面形貌的局部区域,不具有唯一性;分形几何法得到的分形维数是岩石表面形貌的固有参数,不依赖于测定仪器的分辨率和取样长度,具有唯一性。计算分形维数时由于算法的不同,泥岩抛光表面形貌的分形维数不尽相同,功率谱法的计算结果偏大,盒维数法的计算结果偏小,相对而言,三角测量法的计算结果接近于泥岩表面形貌的实际分形维数。
[1] Byerlee J.Frictions of Rocks[J].Pageoph,1978,116(1):615-626.
[2] Jaeger J C.The frictional properties of joints in rocks[J].Pure and Applied Geophysics,1959,43(1):148-158.
[3] 郧建平.基于白光干涉的表面形貌接触和非接触两用测量系统的研究[D].武汉:华中科技大学,2008.
[4] 刘建辉.基于数字图像处理技术的磨粒图像分析与识别方法的研究[D].北京:北京交通大学,2007.
[5] 全书海.基于表面灰度图像的加工表面形貌分形特征研究[D].武汉:武汉理工大学,2003.
[6] 王淑珍.基于白光干涉超精密表面形貌测量方法与系统研究[D].武汉:华中科技大学,2010.
[7] Lee S D,Lee C I,Park Y.Characterization of joint profiles and their roughness parameters[J].International Journal of Rock Mechanics and Mining Sciences,1997,34(3-4):171-174.
[8] 陈国安,葛世荣,张晓云.分形几何与摩擦学进展[J].润滑与密封,1999,(5):69-71.
[9] Majudar A,Bhushan B.Fractal model of elastic-plastic contact between rough surfaces[J].Tram of ASME,1991,113(1):1-11.
[10] 蒋书文,姜斌,李燕,邓宏,郑昌琼.磨损表面形貌的三维分形维数计算[J].摩擦学学报,2003,23(6):533-536.
[11] 葛世荣.粗糙表面的分形特征与分形表达研究[J].摩擦学学报,1997,17(1):73-80.
[12] 葛世荣,索双富.表面轮廓分形维数计算方法的研究[J].摩擦学学报,1997,17(4):354-362.
[13] Buzio R,Valbusa U.Applied Scanning Probe MethodsⅢ[M].Heidelberg,Germany:Springer Berlin Heidelberg,2006.
[14] Hyslip J P,Vallejo L E.Fractal analysis of the roughness and size distribution of granular materials[J].Engineering Geology,1997,48(3-4):231-244.
[15] Jahn R,Truckenbrodt H.A simple fractal analysis method of the surface roughness[J].Journal of Materials Processing Technology,2004,145(1):40-45.
[16] Martan J,Przybylski G,Tabaka R,et al.Fractal analysis of roughness profile induced by ion bombardment of metal surface[J].Vacuum,2005,78(2-4):217-221.
[17] Tanaka M,Komagata M,Tsukada M,et al.Fractal analysis of the influence of surface roughness of toner particles on their flow properties and adhesion behavior[J].Powder Technology,2008,186(1):1-8.
[18] 李小兵,刘莹.表面形貌分形表征方法的比较[J].南昌大学学报(理科版),2006,30(1):84-86.

