隧道软弱围岩的改进BP神经网络位移反分析

高攀科，谢永利

(1.长安大学公路学院，陕西西安710064;2.陕西铁路工程职业技术学院，陕西渭南714099)

0 引言

隧道工程研究对象是复杂的地层环境，常受到断层破碎带及节理裂隙等地质体影响，加之工程开挖、气候等外部环境的影响，人们往往难以获得理想的工程力学参数［1］.位移反分析是以工程现场的量测位移作为基础信息反求实际岩土体的力学参数、地层初始地应力，支护结构的边界荷载等，为理论分析和工程应用提供符合实际的基本参数.位移反分析法是解决岩土体力学参数重要途径之一［2-3］.

人工神经网络(Artificial Neural Network，ANN)方法，具有较强的非线性动态识别和处理能力，在岩土体工程力学参数和变形关系不可知、不确定的情况下，可有效建立二者之间的线性映射关系［4］，能较好帮助人们掌握岩土体工程特性.郝哲等［5］采用FLAC仿真，获取神经网络训练样本，建立基于差分法和人工神经网络的反分析法模型，但上述二者研究中样本获取均来源于数值模拟，如何更加真实反映实际施工值得考虑.朱合华等［6］以隧道施工动态位移为基础，把前施工步测点位移的监测值通过反分析确定所需参数，据此建立有限元仿真模型来预测后施工步位移，取得一些有益的结果.然而，上述研究大多是针对稳定围岩隧道，对于软弱围岩隧道施工位移反分析及其预测的研究相对较少.笔者针对隧道软弱围岩位移与力学参数之间的非线性映射关系，建立基于改进的BP人工神经网络模型进行位移反分析，以期求得合理力学参数，更好地为隧道、地下硐室等地下工程建设服务.

1 人工神经网络

20世纪40年代，人工神经网络的概念被提出，随即引起人们广泛关注.

1.1 神经网络模型

人工神经网络是单个并行神经元的集合，对于一个神经网络，首先应建立神经元模型.将ωij定义为神经元i和神经元j的权值(连接强度)，ui(j=1，2，…n)为神经元 i的输入信号;θi为神经元的阀值或称为偏差;xi为经偏差调整后的值，即神经元的局部感应区.则有

f(xi)为非线性函数，称为激励函数或作用函数;yi是神经元i的输出.

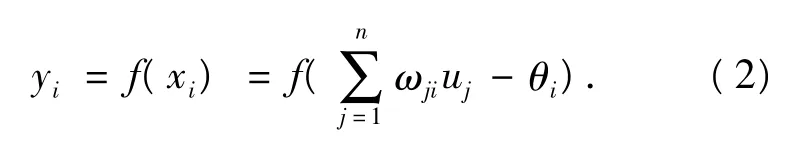
由大量神经元进行连接可构成人工神经网络.神经网络中的神经元连接方式与训练网络的学习算法是紧密结合的，可以认为应用于神经网络设计中的学习算法是被结构化了的，网络的拓扑结构也对网络的特性有重要的影响.图1是多层神经网络模型图.

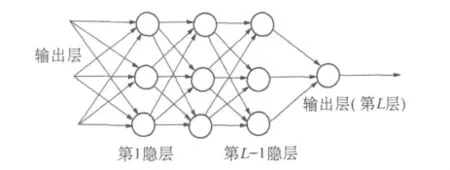
图1 多层神经网络模型Fig.1 Multilayer neural network model

1.2 BP算法的基本原理

神经网络的学习也称为训练，是通过神经网络所在环境的刺激作用调整神经网络的自由参数，使神经网络以一种新的方式对外部环境作出反应的一个过程.学习算法是针对学习问题的规则集合.BP算法(Error Back Propagation algorithm)的学习过程是有工作信号正向传播和误差信号反向传播两个过程组成.正向传播是信息从输入层经隐层逐层传递、处理，至输出层输出的过程，由于权值不变，每一层神经元的状态只能影响到下一层神经元.如果在输出层得不到期望输出，则转入误差信号反向传播过程，误差信号将逆传返回，由反馈的误差调节权值.通过这2个过程的循环，不断修正网络输出，使得误差越来越小，直至满足条件.

2 位移反分析的改进BP神经网络模型

2.1 模型构建的基本思想

首先，针对隧道软弱围岩，进行室内试验、现场试验，设置各力学参数值，采用有限元程序计算出围岩变形，获取一组计算位移数据，经过初始化转换(归一化处理)形成网络训练样本，并选取检验样本.利用这一训练样本训练神经网络直至达到精度条件.此时，神经网络就形成了隧道围岩力学参数和位移之间的映射关系，即位移反分析神经网络模型构建成功.其次，通过现场检测取得隧道软弱围岩位移观测值，利用上述反分析模型反向计算软岩力学参数，即完成隧道软弱围岩的位移反分析.

应当注意的是隧道工程的建设是一个复杂的动态过程，影响因素众多，不但与围岩相关的力学性能参数(弹模E、黏聚力C、内摩擦角φ、泊松比μ、容重γ和埋深h等)相关，还应考虑诸如开挖跨度B、高跨比H/B、开挖进尺L、喷射混凝土厚度D、锚杆设置等工况参数.考虑神经网络模型的稳定性和可靠性，输入参数参数数目过多，将对网络训练十分不利.为此，可将输入参数按照分步、分区的思想，依据上述反分析模型构建过程，逐次进行反演分析.

2.2 BP神经网络的改进

BP神经网络具有对信息的分布式存储，有一定的容错性和抗干扰性，其最主要的特点是具有很强的非线性影射能力和柔性网络结构，得到了广泛的应用.

2.2.1 BP神经网络的缺陷

一般BP网络由于自身网络结构和算法问题，使其存在不可避免的缺陷:①网络结构设计时网络层数，特别是最佳隐层神经元数目的选择尚无成熟理论指导，一般依靠经验选择，不确定性大;②学习算法收敛速度慢，常需要千步以上迭代，甚至更多，消耗时间长;③由于采用梯度优化，往往不能保证取得全局最小值，存在易陷入局部极小问题;④若学习系数和惯性系数选择不当，会使网络学习麻痹.

2.2.2 BP神经网络结构的改进

BP神经网络设计中，隐层单元数的确定与输入层和输出层的单元数有关，且最佳隐层单元数的计算尚无成熟理论指导，一般依靠经验选择，这一定程度上增加的建立位移法分析模型的难度.笔者提出两点改进措施以解决这一难题.

(1)采用数学二分法原理，通过多次试算确定最佳隐层单元数，其原理在文献［9］有详细说明，本文不再赘述.

(2)在传统的神经网络隐层原有神经元输出基础上加入反馈量，使BP网络具有动态处理能力，增强网络的适应性和泛化能力.

式中:yi(n+1)为第n+1次神经元输出;yi(n)为第n次神经元输出;ρ为反馈系数，通常0≤ρ≤1.神经元的输出不仅由本次迭代权值确定，同时考虑了上次迭代的影响，即反馈系数越大第n次神经元输出对第n+1次输出影响越大，反之则越小.本文网络模型调试实践证明反馈系数增强了神经网络的抗干扰能力，进一步强化了网络的适应性和泛化能力.

2.2.3 BP网络学习算法的改进

(1)改进惯性校正法.考虑BP学习算法收敛速度慢，目标函数存在局部极小问题，惯性校正法表述为在每次对权值和阈值进行校正时，可按照一定的比例加上前一次学习时的校正量，即惯性项.这样可以加快网络的学习收敛效果.

式中:Δω(n)为本次应得校正量;d为本次校正量;η为惯性系数;Δω(n-1)为前一次校正量.若惯性系数太大，会削弱误差项的作用，延长收敛作用，引起振荡.为此可将惯性项系数设为变量，随着校正的进行而逐渐增大惯性系数，使被校正量随着学习进程的发展，逐渐沿前一次校正方向变化，为此达到加速收敛的目的.通常η≤0.9.

(2)基于变步长的算法.惯性系数越大，学习效率越高，收敛也越快;但随着η增大，函数收敛易引起振荡.为避免引起振荡，提出变步长的思想.即在训练开始时选较大的η值，然后每次训练结束时，将误差指标E(n+1)与上一次误差E(n)比较，若E(n+1)＜E(n)，则按原步长继续训练，否则，将发生振荡，故可减少步长E(n+1)=E(n)/2，退回上一步重新进行训练计算.

(3)改进误差函数.传统的误差函数表达式见(7)式:

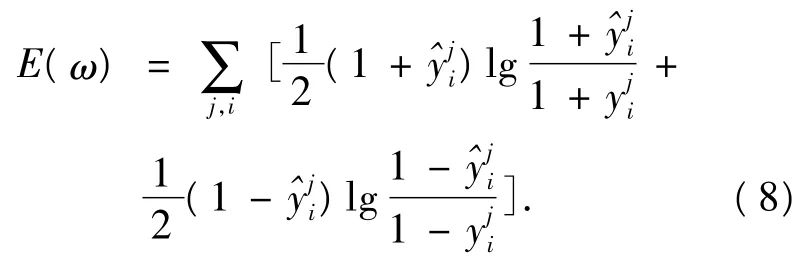
该函数，当yi→±1时，发散，从而避免了传统误差函数式容易产生麻痹的现象.

2.3 具体实施步骤

(1)利用有限元计算形成训练样本和检验样本.

(2)将训练样本参数输入上述神经网络中，经向前传播分析，求出网络输出.

(3)若在输出层得不到希望的输出，则转入反向传播，将误差信号沿原神经元连接通路返回，通过修改各层神经元的权值，逐次地向输入层传播进行计算.

(4)输入检验样本检验，如果不满足要求，继续训练网络，直至满足误差要求，完成神经网络训练.

(5)通过隧道现场监测取得围岩位移的观测值，利用已经训练成功的神经网络，反算围岩力学参数.

3 应用实例分析

3.1 模型分析

笔者为以斑竹林隧道软弱围岩段新奥法施工实践为例［7］，岩土体力学参数经试验室分析确定，采用弹性模量 E=2 200 MPa，泊松比 μ=0.41，黏聚力 C=25 kPa，内摩擦角 φ =24°.对YK35+250～YK35+200段Ⅴ级围岩(软弱的泥质页岩与砂岩互层)开挖及支护过程进行有限元仿真分析，获取关键点部位相关参数(图2).并对所有参数及位移进行归一化预处理，作为网络训练样本和检验样本，进行位移反分析.输入层节点数为 4(E，μ，C，φ)，输出层结果为位移，即输出层节点为1.

图2 隧道反分析关键点Fig.2 Tunnel’s key points of back analysis

3.2 训练结果分析

图3是进行运算的误差收敛情况.从中可以看到误差收敛平稳，基本未见震荡，并在经历局部极点后，达到满足要求误差，经过9 033次迭代训练，系统误差收敛到0.000 1停止.该训练成果很好证明了上述改进措施的效果.

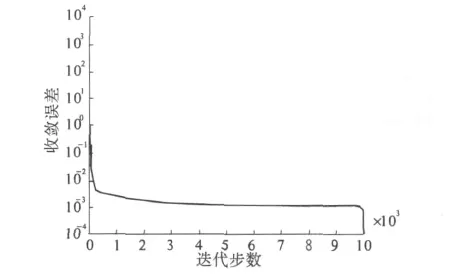
图3 误差收敛曲线Fig.3 Convergence curve of error

利用检验样本122#数据对训练完成的网络进行检验，经检验该网络满足要求.结果分析情况见表1所示.

经改进的BP神经网络已经训练完毕，且完成了检验过称.此时，输入隧道施工现场位移观测值，利用网络保存的映射关系，便可求得相应岩体力学参数.具体结果见表2.

表1 训练结果检验表Tab.1 Testing chart of training result

表2显示，将经神经网络反分析求得岩体力学参数，再次应用于有限元数值仿真，从而计算出隧道软弱围岩位移值.并将现场监测的观测值和反分析计算位移值进行比较，其总体相对误差均在4%以内，显然满足工程需要.

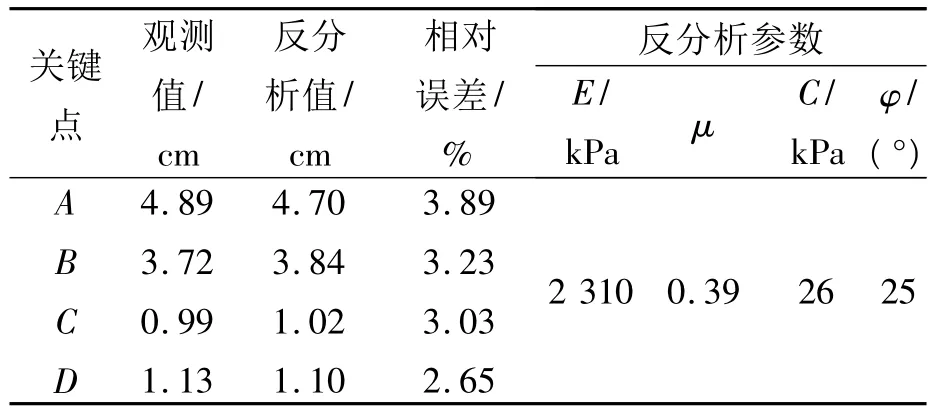
表2 关键点位移反分析结果分析表Tab.2 Result analysing chart of key points’displacements back analysis

4 结论

笔者采用改进的BP神经网络和有限元数值仿真对软弱围岩隧道进行位移反分析，从而确定围岩力学性能参数.实例分析结果表明:

(1)就网络改进方面，采用多种改进措施，使运算误差收敛平稳，且能达到较高精度要求，拟合精度令人满意，具有较高可靠性.

(2)该隧道关键点位移反分析结果显示，反分析数值与观测值相对误差较小，总体在4%以内，证明其结果具有实用性.

［1］冯夏庭，杨成祥.智能岩石力学(2)——参数与模型的智能辨识［J］.岩石力学与工程学报，1999，18(3):350-353.

［2］王芝银，杨志法，王思敬.岩石力学位移反演分析回顾及进展［J］.力学进展，1998，28(4):488-498.

［3］冯夏庭，张治强，杨成祥，等.位移反分析的进化神经网络方法研究［J］.岩石力学与工程学报，1999，18(5):497-502.

［4］高隽.人工神经网络原理及仿真实例［M］.北京:机械工业出版社.2010.

［5］郝哲，刘斌.基于差分法及神经网络的硐室围岩力学参数反分析［J］.岩土力学，2003，24(S2):77-80.

［6］朱合华，张晨明，杨建秀.龙山双连拱隧道动态位移反分析及预测［J］.岩石力学与工程学报，2006，25(1):67-73.

［7］高攀科.斑竹林隧道软弱围岩变形特征与控制措施研究［D］.重庆:重庆交通大学土木建筑学院，2009.