基于齿形法的空间桁架结构抗风优化

黄友钦，王艳萍，傅继阳，林俊宏，吴玖荣

(广州大学广东省结构安全与健康监测工程技术研究开发中心，广东广州510006)

0 引言

空间桁架结构中构件可灵活布置成各种空间外形来满足建筑需要，因此在现代公共建筑中得到了广泛应用［1］.但此类结构通常具有固有频率低、柔性大、阻尼小等特点，是典型的风敏感结构，风荷载常成为结构设计的主要控制荷载［2］.因此，有必要研究这类结构的抗风优化设计方法，使杆件间受力更加协调以节省材料和降低造价.

然而，目前结构抗风优化研究基本集中于高层建筑结构，较少涉及大跨屋盖.Chan等以等效静力风荷载下高层建筑的楼顶和层间位移响应为约束条件，工程造价作为目标函数，采用最优准则法对高层建筑的构件尺寸进行优化［3］.Spence进一步考虑了场地气候概率信息，建立了基于可靠度的抗风优化数学模型［4］.

大跨空间结构的优化中通常设计变量众多，准则法通常被认为是有效方法［5］.笔者首先阐述基于满应力准则的抗风优化设计理论和程序实现，然后介绍用于本研究的双层柱面网壳及其风荷载获得方法，最后基于计算结果讨论了截面积下限、满应力步长等的影响.

1 抗风优化设计理论

空间桁架结构的抗风优化数学模型为:

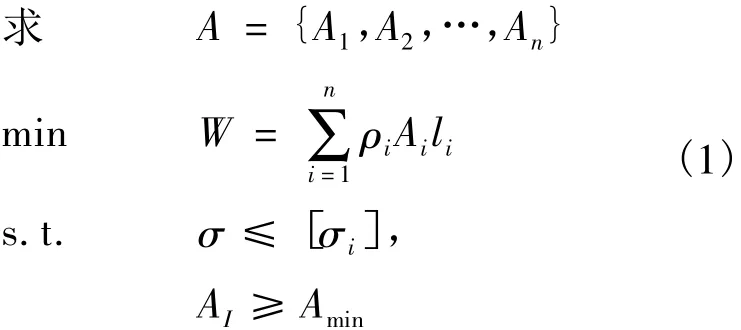
式中:A={A1，A2，…，An}表示所有n根杆件的截面积;W表示结构重量，ρi和li分别表示杆件i的截面积;σi和［σi］分别表示杆件i的风致应力和容许应力;Amin表示截面积下限值，即几何约束下界.

满应力准则法是指通过调整构件的截面尺寸，使各构件的应力尽量达到容许应力，此时认为结构承受荷载的能力被充分发挥，结构达到最优状态［6］.空间桁架结构的抗风优化可按下面步骤进行.

(1)根据结构的初始设计方案确定截面积初值A，且令k=1(k表示迭代次数).

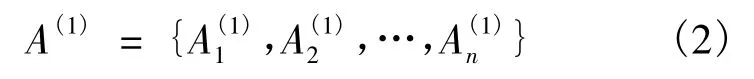
(2)计算杆件应力比.等效静力风荷载下计算杆件的应力，通过与容许应力比较来得到应力比，并选择非零杆进行优化.

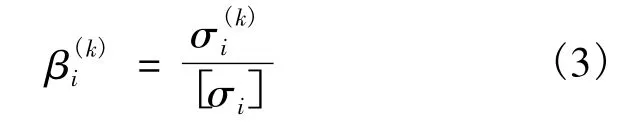
(3)走射线步.由于结构最优解位于主约束曲面，所以为了能够得到最优解，应使迭代点落在主约束曲面上，因此在两次应力比计算之间增加射线步使所有杆件满足约束条件［6］.

(4)判断是否终止迭代.为了判别设计点是否为最优点，可在每次射线步后记录一次结构重量，当发现经某一射线步后结构重量大于前一次的重量时，就取前一次的设计点为最优点.射线步后通过下式计算结构重量.

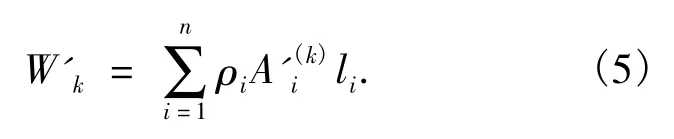
(5)走满应力步.走射线步后若计算未收敛则需要将应力比还原至原本值，即将各杆件的应力同时改变β(k)max倍以得到下次迭代的截面积初值.

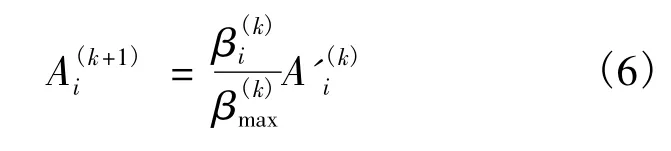
当满应力步的步长太大时，可能会错过真正的最优解，而使所求解远离最优解，因此可通过修改应力比来缩短满应力步长，使相邻两射线步的迭代点之间相距更近，从而提高最优解的精度.可通过下式来缩短满应力步长.式中:λ为修改系数，其值越大表示对满应力步长的改变越小.

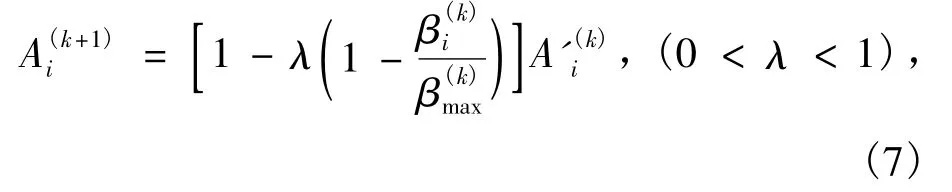
(6)越界处理.当某些杆件的截面积小于几何约束中的截面积下限值时，可由下式进行截面积修正.

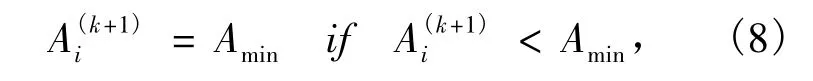
进行越界处理后获得更新的杆件截面积，再回到步骤(2)进行下一次迭代计算，直至结构重量出现增加而停止迭代.

基于MATLAB数值计算平台编制优化计算程 序 (Wind ResistantOptimization Program，WROP)，整合了等效静力风荷载、风致响应和优化计算等三个部分［7］.

2 结构简介及风荷载

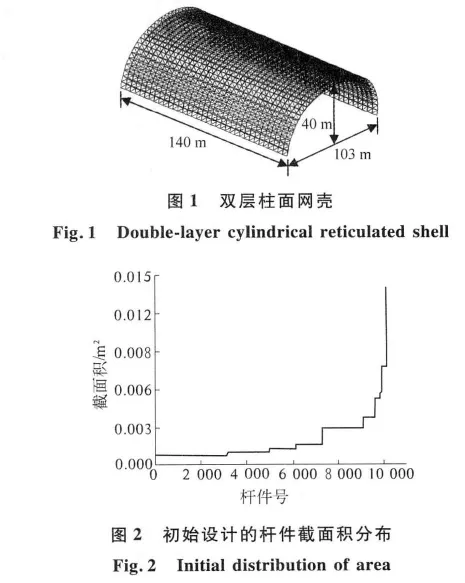
用于分析的空间桁架结构为正放四角锥双层柱面网壳，高度和跨度分别为为40 m和103 m，长度为140 m，采用纵向边缘落地支承［8］.结构中杆件的布置如图1所示，杆件总数为10 080，节点总数为2 592，初始总重量为603.5 t.杆件间的连接视为铰接，杆件截面积的最大值为1.41e-2 m2，最小值为8.51e-4 m2.杆件的弹性模量和密度分别为206 GPa和7 850 kg/m3.初始设计的杆件截面积分布如图2所示，将初始截面积作为优化设计的初值A(1)，将其最小值8.51e-4 m2作为几何约束下界Amin.

风洞试验是获得结构上风荷载的有效方法，该双层柱面网壳的刚性模型测压风洞试验在同济大学TJ-2风洞中完成，每隔10°在90°～180°之间进行7个风向角的测试［8］.基于试验得到的非定常风荷载进行平稳激励随机振动分析可得到结构上的等效静力风荷载［9］.

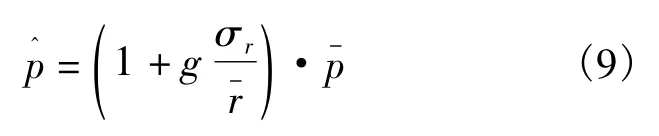
考虑到风向角为150°时结构的风效应较为显著，因此选取150°风向角下的等效静力风荷载=1.6进行优化计算.图3给出了计算该风向等效静力风荷载时得到的应力峰值杆件的应力响应功率谱.

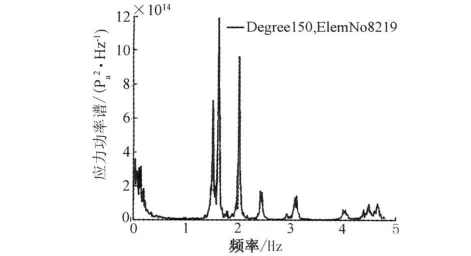
图3 150°风向下杆件的应力响应功率谱Fig.3 Auto-power spectrum of stress at 150°

3 优化结果与讨论

以初始设计截面对应的风致应力最大值作为所有杆件的约束容许应力，采用编制的计算程序对双层柱面网壳进行抗风优化.以下给出优化计算结果并对关键参数进行讨论.

3.1 优化计算结果

优化计算76次后迭代停止，图4给出了结构总重和最大应力比随迭代次数的变化.可以看出，结构重量约降低48%，最大降幅发生在首次迭代;最大应力比的变化较为平稳，由1.18逐渐稳定至收敛值.因此，通过设置射线步保证了所有杆件的应力均小于容许应力，即不违反强度约束.

3.2 截面积下限的影响

图5给出了λ=1.0且不设几何约束下界时第2次迭代中射线步得到的杆件应力比和截面积.由图可见，最大应力比为6.21，远大于设定截面积下限时的1.18.同时，由于未设定截面积下限，满应力步后的最小截面积仅为3.03e-8 m2，小于规范允许值［10］.

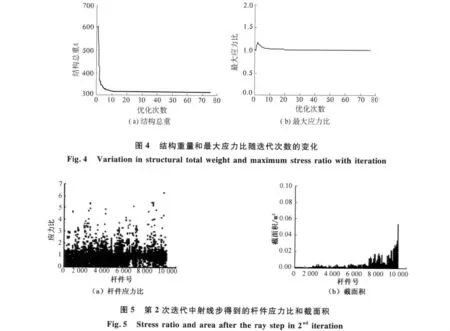
迭代4次后结构重量出现增加，因此取第4次迭代中射线步的结果作为优化结果.表1给出了优化过程中杆件的最大应力比、截面积和结构重量的变化，并与设定几何约束下界的结果进行比较.可以看出，不设截面积下限时，随着迭代进行，杆件的最小截面积远小于约束下限值(仅为1.25e-12 m2)，而最大杆件截面积(4.84e-2 m2)却大于设定截面积下限时的结果(1.12e-2 m2)，从而得到的结构总重反而大于设定截面积下限的结果.因此，在复杂桁架结构的抗风优化中，虽然射线步已将迭代点拉回主约束曲面，但仍有必要设定截面积下限来使各杆件间的受力更加协调，从而充分利用材料性能.

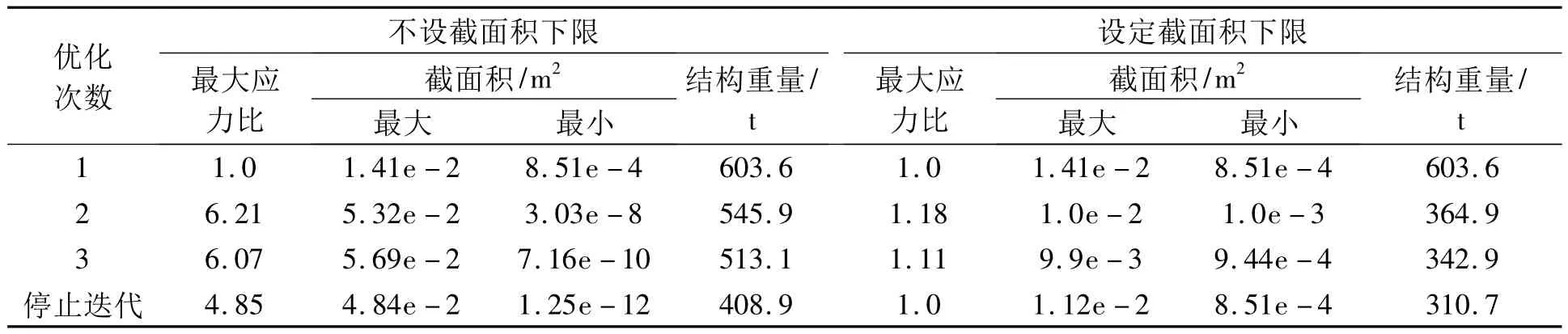
表1 前3次迭代和停止迭代时的部分计算结果Tab.1 Results of the first 3 and final iterations

3.3 满应力步长的影响

λ=0.5时，第1次迭代中满应力步后的杆件应力比和截面积如图6所示.显然，将满应力步长折减后应力比的范围变小，提高了应力比的最小值，从而增大了杆件截面积的最小值.

图7给出了λ=0.5时结构总重随迭代次数的变化.对比图4可见，优化得到的结构重量与未修改满应力步长的结果接近，这是因为设定截面积下限时杆件的最大应力比本身较小，故优化结果对满应力步长缩短并不敏感.由于第2次迭代时最大应力比就已十分接近1.0，因此计算收敛所需迭代次数小于未修改满应力步长的情况.

图6 第1次迭代中满应力步后的应力比和截面积Fig.6 Stress ratio and area after the full stress step in 1st iteration

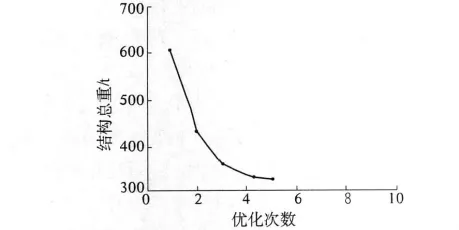
图7 结构重量随迭代次数的变化Fig.7 Variation in structural weight with iteration

4 结论

(1)优化设计使网壳总重降低了约48%，所有杆件的应力均小于初始设计下的最大应力值，因此在满足初始设计要求的前提下使结构总重有效降低;

(2)通过设定设计变量下限避免了优化得到的杆件截面积小于规范容许值，且使杆件间受力更加协调，充分利用材料性能;

(3)对于最大应力比并未明显超出可行范围的情况，优化结果对满应力步长并不敏感，但通过修改满应力步长可能使迭代次数减少.

［1］LU Chun-ling，LI Qiu-sheng，HUANG Sheng-hong，et al.Large eddy simulation of wind effects on a longspan complex roof structure［J］.Journal of Wind Engineering and Industrial Aerodynamics，2012，100(1):1-18.

［2］孙文斌，孙芳锦.大跨度屋盖风振控制的遗传算法［J］.郑州大学学报:工学版，2012，33(1):40-42，50.

［3］CHAN C，HUANG Ming-feng，KWOK K.Stiffness optimization for wind-induced dynamic serviceability design of tall buildings［J］.Journal of Structural Engineering-ASCE.2009，135(8):985-997.

［4］SPENCE S，GIOFFRE M.Large scale reliabilitybased design optimization of wind excited tall buildings［J］.Probabilistic Engineering Mechanics， 2012(28):206-215.

［5］钱令希.工程结构优化设计［M］.北京:科学出版社，2011.

［6］朱杰江.建筑结构优化及应用［M］.北京:北京大学出版社，2011.

［7］BATHE K.Finite element procedures［M］.New Jersey:Prentice-Hall Inc.，1996.

［8］顾明.浙江省华能玉环电厂干煤棚风效应研究［R］.上海:同济大学土木工程防灾国家重点实验室，2006.

［9］DAVENPORT A.Gust loading factors［J］.ASCEJournal of Structural Division，1967(93):11-34.

［10］中华人民共和国建设部.JGJ 61—2003网壳结构技术规程［S］.北京:中国建筑工业出版社，2003.