软土超深基坑失稳破坏的离心模型试验研究

冯 虎，高丹盈，刘国彬，马险峰

(1.郑州大学土木工程学院，河南郑州450001;2.同济大学地下建筑工程系，上海200092)

0 引言

软土具有颗粒细、抗剪强度低、含水量高、天然孔隙比大、灵敏度高、高压缩性和流变性等工程特性，土体经扰动后强度明显降低，且在长时间内存在固结和次固结沉降.因此，软土基坑的稳定安全问题显得格外突出［1-2］，尤其是对于开挖深度20 m以上的软土超深基坑，尚未形成完整的设计理论，其失稳破坏机制及影响因素、稳定性验算方法等都有待进一步研究［3-4］.离心模型试验可以在高速离心场下模拟基坑开挖过程，其应力水平与现场相当，文献［5-6］开展了这方面研究，证明其适合于研究基坑的开挖问题，探讨周边建筑对软土超深基坑变形的影响.笔者通过离心模型试验模拟挖深24 m的软土深基坑开挖施工过程及失稳破坏，研究软土超深基坑稳定影响因素、破坏特征与征兆等，为判断基坑稳定安全状态提供依据，为研究软土深基坑稳定性分析方法提供试验数据.

1 离心模型试验方案

1.1 土样制备

试验选用了上海地区具有代表性的第④层淤泥质黏土和第⑦层粉细砂土作为需要模拟的开挖土层.其中第④层土厚39 cm，第⑦层土厚19 cm.为了便于固结排水，形成双排水通道，在土箱的底部铺设一层2 cm厚的黄砂.试验前对土样进行了含水率测定，第④层土含水率为41%，第⑦层土含水率为22.0%.在试验室里将第⑦层土按照土水的质量比为10∶1(ω=32.1%)进行调制，第④层土按照土水质量比为3∶1(ω=67%)进行调制，然后搅拌均匀后按照断面土层分布采用分层固结法进行固结形成重塑土.先对于第⑦层粉细砂土固结，再对第④层土进行固结，其固结度利用固结时间与含水率进行控制.

1.2 模型率的选取

考虑要保证基坑外部横向有不受基坑开挖影响的足够土体和模型箱净空尺寸，试验选取的模型率n=100，即离心机稳定运转时加速度为100 g.

1.3 试验模型设计

试验三组模型分别模拟连续墙深度52、43、38 m，墙厚1.0 m，开挖深度24 m，插入深度比1.14、0.8、0.6.八道支撑，第一道为混凝土支撑，界面尺寸1.0×0.8 m，第二至八道为φ609钢管支撑，壁厚16 cm.土层以上海典型土层适当简化，上部39 m为④层淤泥质黏土、下部19 m为⑦层粉细砂.根据模型比例关系，模型中基坑开挖深度24 cm，土层厚度60 cm(最下面2 cm为黄砂，固结排水用)，挡墙深度分别为52、43和38 cm，挡墙和支撑用铝板和铝管模拟.

试验中量测坑外地表沉降、挡墙应变、土压力和坑底隆起量.

图1为三组模型的示意图，考虑到对称特性，取基坑半结构进行试验.

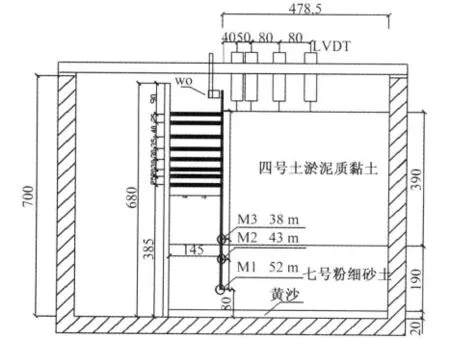
图1 试验模型示意图Fig.1 Experiment model diagram

1.4 模型围护结构设计

(1)地下连续墙

本次离心模型试验中，采用铝板模拟地下连续墙，根据材料抗弯刚度等效相似原则，确定替代材料板的厚度［7］，即

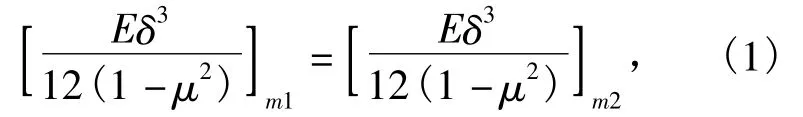
式中:E为弹性模量;δ为挡墙厚度;μ为泊松比;m1表示与原型P相同的模型材料，μm1=μp，Em1为模型替代材料，经推导计算，模型铝板厚度为6.5 mm，模拟的地下连续墙厚度1 000 mm.

(2)混凝土支撑和钢管支撑

现场水泥混凝土支撑与钢支撑均采用铝管模拟，根据抗压刚度等效的原则可确定模型试验中模拟支撑的铝管直径和壁厚.

钢管支撑

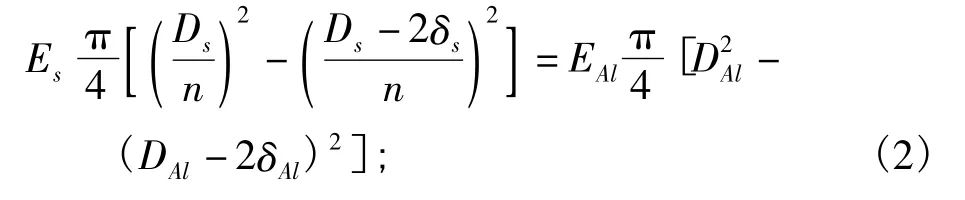
混凝土支撑

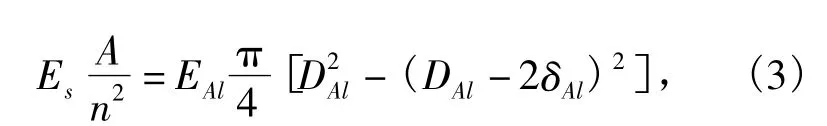
式中:Es为混凝土或钢支撑弹性模量;δs为钢支撑壁厚;A 为混凝土支撑截面积;EAl，DAl，δAl为模型试验中铝管的弹性模量、直径和壁厚;混凝土支撑截面尺寸1.0×0.8 m，强度等级C30;模量为Es=3.0×104MPa;钢管支撑为φ609钢管支撑，壁厚16 cm，计算得到:第一道撑直径取12 mm，第二至第八道钢管撑取8 mm，壁厚都取2 mm.

1.5 试验设备及主要仪器

(1)同济大学TLJ-150土工离心机.本试验是在同济大学岩土及地下工程教育部重点实验室完成，实验室配置了TLJ-150复合型土工离心机，其最大加速度为200 g，最大载重2 t，转臂形式不对称.

(2)电阻式应变片及地下连续墙变形的量测.地下连续墙的侧移在实际工程中是通过测斜管测得.本试验采用基于宽带光源的布拉格光栅形变原理的多点光纤传感器测应变，通过曲线应变换算曲率半径，推导曲线变形公式，从而计算得到地下连续墙的变形.

试验所采用的应变片是由浙江黄岩测试仪器厂生产的BX120-6AA型电阻式应变片，应变片电阻值120±1%，灵敏系数2.08±1%，栅长×栅宽:6×4 mm.

(3)地表位移的量测.位移传感器是由西南结构力学研究所研制生产的差动式位移传感器(LVDT)，测杆形式为弹簧复位，量测分为30和50 mm，精度0.1%FS，电源 ±12 V，输出(-2～ +2)V.

(4)土压力的量测.本试验采用微型土压力盒，微型土压力传感器由西南结构力学研究所制造，规格是外径8 mm，厚2 mm，量程1 MPa，输入电源5 V，输出0～2 V，非线性度0.07%FS，经标定后使用.

2 试验数据分析

2.1 试验土层室内土工试验结果

离心模型试验是在重塑土的环境中模拟基坑开挖过程，重塑土的性质直接关系到试验结果，因此必须对重塑土的性质进行评价，以便对试验误差进行估计，同时对模型与原型的近似程度进行评判.为了减少对试验土体的扰动，在模拟基坑开挖刚刚结束后就进行取样测试抗剪强度和含水量.将土样抗剪强度指标和含水量汇总成表1.

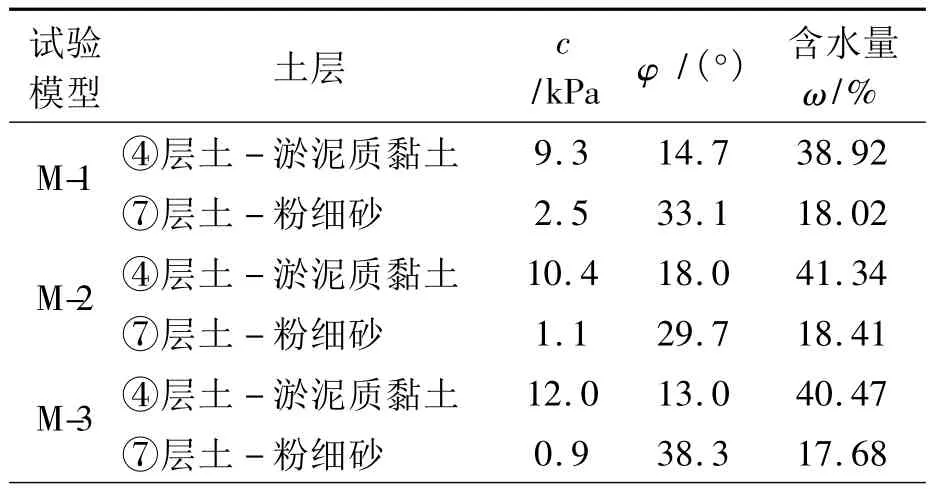
表1 模型土样直剪试验结果Tab.1 Direct shear test results of soil samples

2.2 地下连续墙水平位移

模型M-1和M-2地下连续墙水平位移曲线如图2.挡墙水平位移最大点随基坑开挖面的下移而下移.墙体水平位移是根据铝板上的应变值计算得到的，最靠下的应变片距离墙址有一段距离，墙址水平位移不能直接得到，可以将试验数据的曲线延伸到实际挡墙深度处得到墙体踢脚，可以发现，踢脚相当小，说明墙体插入到⑦层粉细砂硬土层中以后，墙趾的嵌固作用非常明显，对控制墙趾变形非常有利.同时对比两组试验数据可以看出，虽然插入深度不同(M-1为13 m，M-2为4 m)但是最大变形相近，这说明墙趾插入到⑦层硬土中一定深度再增加对墙趾和墙体总体变形的影响不再显著.墙趾插入⑦层硬土层中墙趾嵌固作用下对踢脚控制非常有利，进而也对基坑的稳定性有明显的贡献.

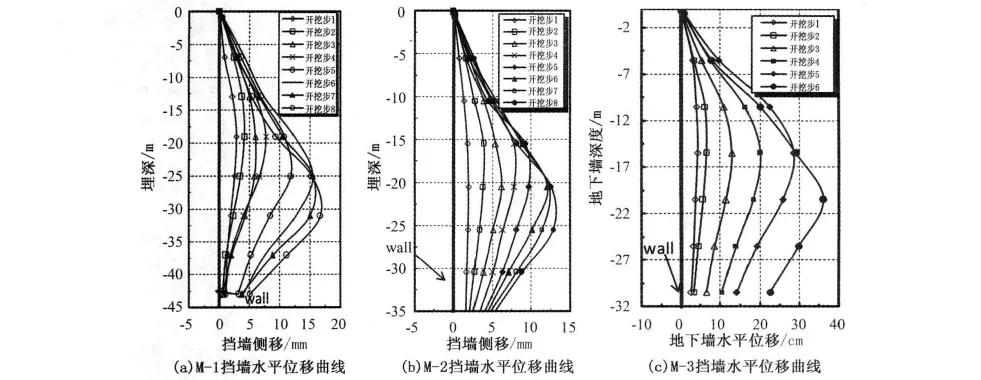
图2 M-1、M-2、M-3挡墙水平位移曲线Fig.2 Horizontal displacement of different retaining wall

模型M-3墙体没有插入硬土层⑦层中，全部位于4层软弱的淤泥质黏土中，在开挖步7过程中失稳破坏.在开挖步6就出现很大的变形，有失稳、坍塌的征兆.开挖步6时墙体水平位移达到了36.17 cm，开挖面以下的墙体变形急剧增加，将测斜曲线顺延可以得到墙趾真正的“踢脚”为12 cm左右，大概等于最大测斜值的1/3.

2.3 地表沉降

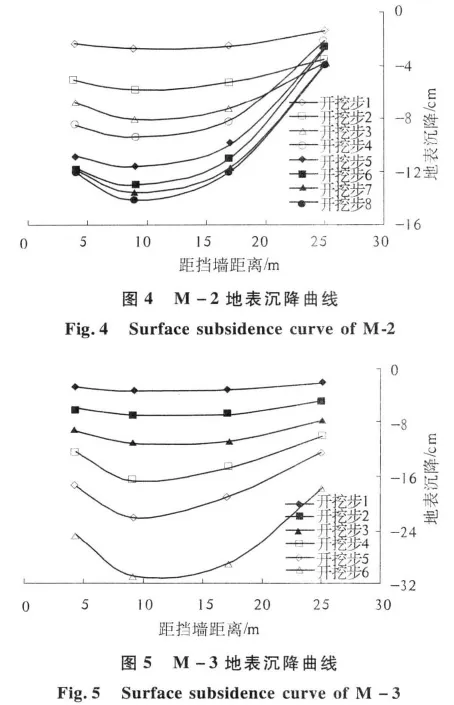
图3和图4分别是模型M-1、M-2地表沉降曲线.随着开挖深度增加，地表沉降随之增大，沉降曲线呈现凹槽型.在开挖后期，地表沉降变化量变小，变形趋于稳定，相对最大沉降量分别为1.6Hmax、1.16Hmax(Hmax为对应的墙体最大水平位移)，或1%H、0.59%H(H为基坑的最终开挖深度).

模型M-3地表沉降曲线如图5所示，变化规律与前两组有明显不同，随着开挖的进行，地表沉降增加的越来越快没有收敛的趋势，开挖步6时，地表沉降急剧增加到31.09 cm，即1.73%H(H为开挖深度)，可以看出基坑正向失稳破坏发展.继续进行第7次开挖，离心机加速过程中基坑坍塌、失稳破坏.

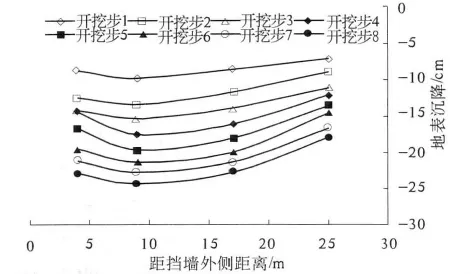
图3 M-1地表沉降曲线Fig.3 Surface subsidence curve of M-1

3 临界开挖深度

模型M-3进行第七次开挖中，在离心机启动加速阶段，地下连续墙出现严重踢脚，之后基坑坍塌，实际上没有达到第七次开挖的开挖深度.基坑极限平衡状态的临界开挖深度，介于第6步和第7步对应深度之间即17～22 m.根据郑颖人［8］数值分析边坡稳定性时采用的判据，笔者将地表沉降的不收敛作为破坏的标准.

模型M-3地表最大沉降点处的沉降值与开挖深度关系见图6，随着开挖进行，地表沉降越来越大，将曲线竖向渐近线定义为坍塌时的开挖深度，对应的地表沉降无穷大.

图中曲线方程

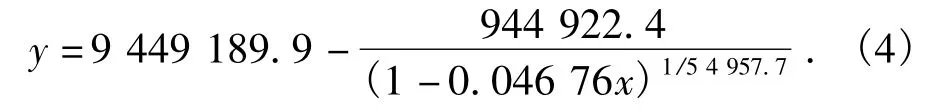
该函数渐近线方程为x=21.38 m，如图6所示，即模型M-3临界开挖深度为21.38 m，挡墙深度38 m，对应墙体插入深度为16.62 m，临界插入深度比为0.78.将其作为上海软黏土中墙址不进入硬土层时挡墙的临界插入深度比.

模型M-2挡墙插入硬土层⑦粉细砂层中4 m，完成既定开挖深度24 m时对应的插入深度比为0.8，与M-3极限破坏状态的插入深度比0.78非常接近，但距离失稳破坏尚远，对比可知墙趾进入硬土层⑦粉细砂层显著提高了基坑稳定性.

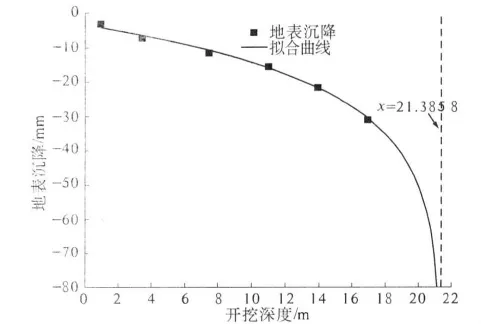
图6 开挖深度与地表沉降关系Fig.6 Curve of Excavation depth of relationship with the surface subsidence

4 基坑失稳破坏征兆

通过对试验数据和现象的总结，得到以下失稳破坏征兆，可以据此判断软土超深基坑稳定安全状态.

(1)墙体水平位移

墙体水平位移快速增加，“踢脚”明显，“踢脚”量值约为墙体最大变形值的1/3.

(2)地表沉降

地表沉降急剧增加到1.73%H(H为开挖深度)，坑外土体局部剪切破坏出现大变形，伴随地面有大量横裂缝出现，进一步开挖基坑坍塌、失稳破坏.考虑到实际地层中分布着其他稍好土层，将地表沉降值乘上折减系数0.8等于1.38H，作为地表沉降控制值.

(3)被动区土压力

坑内土体被挖卸载，被动区土压力减小，但受地墙的挤压作用，被动区土压力侧向系数呈增加趋势，当土压力系数逐步增加到一定值(理论土压力系数附近)时，达到被动极限状态，如图7所示.当被动区土体全部进入极限状态时基坑处于坍塌临界状态.

(4)坑底隆起

坑内土体在土体卸载回弹、坑外土体绕墙趾流入和挡墙挤压等作用下隆起.临近破坏步坑底隆起量为55.8～68.4 cm，即3.1～3.8%H(开挖深度)，坑底靠近挡墙的土体隆起大于基坑中部，坑底土体进入塑性隆起状态，再进一步发展，基坑失稳破坏、坍塌.

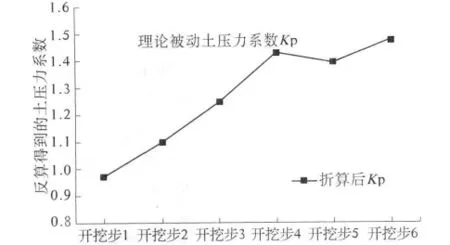
图7 M-3-被动区土压力系数Fig.7 Earth pressure coefficient of the passive zone

5 基坑失稳破坏特征分析

根据试验时标示的滑裂面，见图8，滑裂面绕过墙趾，整个滑裂面可以分成两部分，下半部分形状与抛物线或椭圆相近，比圆弧要扁长，坑内外对称分布，在坑内贯穿坑底;坑外上半部分滑裂面贯穿地面，与地表沉降曲线曲率最大处相交，交点位于地面最大横裂缝附近.从破坏特征，根据文献［9］对深基坑事故类型的分类，M-3属于隆起失稳破坏.

图8 第7开挖步基坑破坏总体特征Fig.8 7th Excavation step instability and failure characteristic

所有支撑都不同程度松动，并与挡墙明显错位.挡墙上抬明显，并且下部被坑外土体推动，整个墙体倾斜顺时针旋转一定角度，见图8、9.坑内土体在卸载、地墙挤压、坑外土体流入作用下，隆起量非常大，隆起土体将最后两道支撑(第6、7道支撑)冲掉，并将其部分掩埋，见图10.

6 结论

通过三组离心机模型试验，研究了软土超深基坑变形、稳定特性.

1)墙趾插入硬土层中，墙趾处的嵌固作用对“踢脚”变形控制非常有利，也提高了基坑的稳定性.

2)墙趾插入到硬土层中一定深度以后再增加插入深度对墙趾和墙体总体变形的影响都将不再显著.

3)对于上海典型软黏土，墙址不进入硬土层时，挡墙临界插入深度比为0.78.

4)软土深基坑失稳破坏征兆特征:

(1)墙体水平位移快速增加，“踢脚”明显，“踢脚”变形量值约为墙体最大水平位移的1/3.

(2)地表沉降急剧增加到约1.38%H(开挖深度)，伴随坑外地面有大量横裂缝出现.

(3)坑底靠近挡墙的土体隆起大于基坑中部，进入塑性隆起状态，最大隆起量达到3.1～3.8%H(开挖深度).

(4)基坑失稳破坏时被动区土体处于被动土压力极限状态.

5)软土超深基坑隆起破坏滑裂面特征:滑裂面通过墙趾，滑裂面下半部分形状与抛物线或椭圆相近，较圆弧扁长，坑内外对称分布;坑外上半部分滑裂面贯穿地面，与地表沉降曲线曲率最大处相交，且交点位于地面最大横裂缝附近.

［1］GOH A T C.Estimating basal-heave stability for braced excavations in soft clay［J］.Journal of Geotechnical Engineering，ASCE，1994，120(8):30-36.

［2］秦会来，黄茂松，王卫东.非均质软土基坑抗隆起稳定性的极限分析方法［J］.岩土力学，2008，29(10):2719-2724.

［3］赵锡宏，杨国祥.大型超深基坑工程实践与理论［M］.北京:中国建筑工业出版社，2004:01-06.

［4］冯虎.软土地区超深基坑抗隆起稳定计算方法研究［D］.上海:同济大学土木工程学院，2010:30-36.

［5］BOLTON M D，POWRIE W.Collapse of diaphragm walls retaining clay［J］.Geotechnique，1987，37(3):335-353.

［6］刘金元.软土基坑的离心模型试验研究(博士学位论文)［D］.上海:同济大学土木工程学院，1999:01-06.

［7］丁春林，周顺华，张师德.基于离心模型试验的承压水基坑变形稳定影响因素［J］.同济大学学报，2005，33(12):1586-1591.

［8］郑颖人，赵尚毅，宋雅坤.有限元强度折减法研究进展［J］.后勤工程学院学报，2005(03):1-6.

［9］刘国彬，王卫东.基坑工程手册［M］.2版.北京:中国建筑工业出版社，2009:121-122.