灭火救援最优路径算法探究

梁 溪

（海南省公安消防总队司令部信息通信处,570100）

0 引言

随着我国经济以及城市化建设的快速发展，我国城市人口、财富、生产、建筑越来越趋于集中化，火灾的发生极容易产生巨大的经济损失以及人员伤亡。现代城市消防灭火救援系统中的一项重要任务就是决定最优的消防出警路线，所谓最优出警路线即消防车能在火灾事故发生时，在最短的时间内达到火灾现场进行灭火救援行为。

目前，最短路径算法发展已经趋于完善，其中有十几种最短路径算法被国内外学者普遍研究，其中包括迪杰斯特拉Dijkstra算法、启发式A* 算法、动态规划方法、神经网络、蚁群算法、遗传算法、进化算法以及DNA算法等。本文在深入研究了Dijkstra算法的基础上，提出了一种新型的改进Dijkstra算法。

1 经典Dijkstra算法

1995年，荷兰数学家E.W.Dijkstra首次提出了Dijkstra算法，它是目前在求解最短路径问题上理论最完善、应用最广泛的一种经典算法。

经典Dijkstra算法可描述如下：

（2）T←N；

（3）从T中选取具有最小权的结点k，d(k)=min[d(j),j∈T]；S(k)=permanently labeled；

（4）如果得到k=t，表示算法结束 ；

（6）T←T={k}，转到步骤（3）。

2 改进Dijkstra算法

2.1 存储结构的优化

在实际交通路网中，道路大多数为单行车道，道路具有方向限制，所以我们应该使用有向图来表示交通路网。而且，交通路网中每个道路结点所连接的路段一般为3-5个，属于稀疏图。此时，更适合使用邻接表存储结构，该存储结构具有节省空间、易于实现且易于扩充更新数据域等优点，且更加能全面真实的反映路网特征方面。

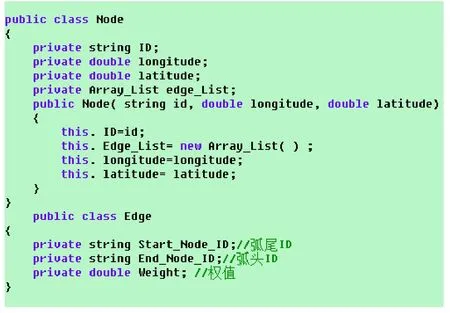
有向图中的结点Node类可描述道路交叉口，有向图中的弧Edge类可描述路段。所有路段的距离即Edge的长度可以用Mapinfo软件中自带的测距函数来实现测距功能。其中，每个节点包含以下信息：结点编号ID、结点的出边表edge_list、longitude、latitude等。而每条弧要包含以下信息：弧头ID（Star_Node_ID）、弧尾 ID（End_Node_ID）以及权值 Weight。

用C#语言描述邻接表存储结构：

2.2 搜索区域的限定

减小算法的搜索规模是提高算法效率的一项关键技术。Nordbeck根据交通路网的特性提出了基于椭圆限制的最优路径算法，设交通路网中起点为S，终点为D，中间的某个节点为N，N与S之间距离为 ，N与D之间距离为 ，则限制条件为。此时，则形成了一个椭圆形的搜索区域。该方法虽然减少了搜索结点，但并没有提高算法的效率，非线性运算增加了算法的运算量。王晓丽提出了基于平行四边形限制的最优路径算法，这种方法省去了非线性计算，但是仍然在计算量上有很大的增加，因为椭圆变成多边形要经过坐标轴旋转和平移等过程。

本文提出了一种简单易于实现的区域搜索限制模型，设给定起点为S，终点为D，则区域搜索限制模型可由公式(1)描述：

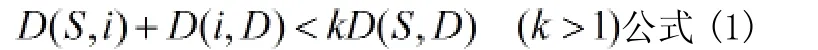
D(i ,j)为Mapinfo中自带的测距函数，表示的是节点i与点 j之间的几何距离，是由结点的地理坐标直接计算得出。k为区域控制参数，k越大，搜索区域越大，搜索出最优路径的几率也就越大，计算量也越大，反之则得到最优路径的几率就越小，计算量越小。所以，选择一个合适的k值显得至关重要，既可以避免搜索区域过大结点过多，又可以搜索到最优路径。

2.3 双向查找规则

为了得到更快速的搜索过程，本文在考虑规则的基础上，提出了双向查找规则应用于最优路径搜索系统中。双向查找规则的基本思想是从两个端点同时开始搜索，相遇后即停止搜索，这样，搜索速度较之单向搜索快了一倍，路径减少了一半。设 D(S,i)、D(N,i)分别为起点S和终点N到结点i的最短路径的长度，P(S,i)，P(N,i)分别表示从 S,N 到结点i的前一结点的最短路径的长度。每个结点都存在一个标号｛D(S,i),P(S,j ),D(N,i),P(N,i )｝。

3 实验结果及分析

本文将改进Dijkstra算法进行试验验证，试验数据取自于市区地图数据，经过处理后得到符合项目要求的路网数据。其中节点数为3187，路段数为4515。试验得到传统Dijkstra算法和优化Dijkstra算法的搜索结果比较如表1所示。根据源点和终点的不同，表1列出2组数据。

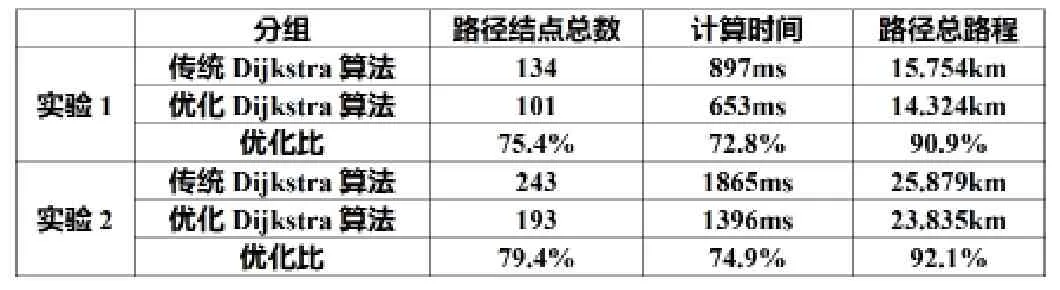
表1 实验对照表

4 结论

本文在基于传统的Dijkstra算法的基础上，提出了三个方面的优化策略，分别是搜索区域的限定、存储结构的优化以及双向查找规则。改进后的Dijkstra算法具有节省存储空间以及提高算法运行效率的优点。本文提出的优化算法是针对算法本身的，对于实际的消防出警有一定的理论参考，但是在实际应用中，实时的交通信息对最优路径的选择存在很大的影响。随着全球定位系统和路径导航系统的不断发展，研究更加符合实时交通的消防灭火救援最优路径有着重大的现实意义。

[1]唐文武,施晓东,朱大奎.GIS中使用改进的Dijkstra算法实现最短路径的计算[J].中国图象图形学报,2000,5(12): 1019～1023.

[2]Amit.Amit ’s notes about path-finding [Z].http://www-cs-students.stanford.edu/～amitp/gameprog.html.

[3]梁娟,郭军丽,魏勇.利用动态规划算法求解最短路径[J].河南机电高等专科学校学报,2006,14( 5):30～31.

[4]纪其进.一种基于脉冲耦合神经网络的最短路径算法[ J].小型微型计算机系统, 2005, 26(5): 826～829.

[5]黄贵玲,高西全, 靳松杰,谈飞洋.基于蚁群算法的最短路径问题的研究和应用[J].计算机工程与应用,2007,43(13) :233～235.

[6]孙霞,黄席樾,杨祖元,向长城.基于改进遗传算法的城市交通动态最优路径求解[J].计算机工程与应用,2007, 43(30) :245～248.

[7]冯琦, 周德云.基于微分进化算法的时间最优路径规划[J].计算机工程与应用, 2005, 12: 74～75,222.

[8]许进,张雷.DNA计算机原理、进展及难点(Ⅰ):生物计算系统及其在图论中的应用[J].计算机学报,2003,26(1): 1～11.

[9]NORDBECKS, RYSTEDT B.Computer Cartography Shortest Route Programs[M].Sweden:The Royal University of Lund,1969.

[10]王晓丽, 杨兆升,吕旭涛,等.平行四边形限制最短路径算法及其在交通网络中的应用[ J].吉林工业大学学报, 2006,36(1):123-127.