基于坐标系变换的并网锁相环性能分析
杨国韬 孙志毅 刘立群
(太原科技大学电子信息工程学院,山西 太原 030024)
0 引言
目前,在电力电子装置中广泛应用的锁相环一般分为两种方法。其中一种方法是采用硬件电路检测电网电压过零点求得相位差信号,然后用硬件或软件实现锁相[1-2]。但由于每个工频周期内电网电压只有两个过零点,限制了锁相速度,而且电网电压本身的畸变和检测电路的各种干扰信号,使硬件锁相环电路很难准确检测到过零点,从而使输出的相位信号产生振荡。另一种方法是基于同步旋转坐标变换的软件锁相环(software phase-locked loop,SPLL),常用的包括单同步坐标系软件锁相环(single synchronous reference frame software phase-locked loop,SSRF-SPLL)[3]、双同步解耦软件锁相环(decoupled double synchronous reference frame software phase-locked loop,DDSR-SPLL)[4]和增强型软件锁相环(enhanced phase-locked loop single synchronous reference frame software phase locked loop,EPLL-SSRF-SPLL)[5]。
锁相环算法的优劣直接决定了发电系统并网能力的好坏。针对目前常见的三种基于d-q坐标变换的锁相环算法,有必要分析它们在不同电网故障下的并网能力和优缺点,特别是在电网电压存在畸变或者不平衡的情况下,选取最适合的锁相技术可以有效提高系统并网能力。
1 三种锁相环原理及模型
1.1 SSRF-SPLL 原理
单同步坐标系软件锁相环(SSRF-SPLL)算法是基于跟踪电网正序分量而提出的。当电网平衡或者频率突变、电压偏转等电压不平衡时,该算法能够实现迅速锁定频率和相位[6]。其具体算法为:首先将由三相电网电压ua、ub、uc所在的三维坐标系转换到两维静止坐标系 α-β上;然后通过旋转坐标系,使得两维静止坐标系α-β变换为两维动态坐标系d-q,坐标系d-q以ω'的角速度逆时针旋转。SSRF-SPLL矢量图和模型图如图1所示。

图1 SSRF-SPLL矢量图和模型图Fig.1 Vector and model diagrams of SSRF-SPLL
假设电网电压矢量us的幅值不变,使us与d轴同向,可以实现锁相的效果。为了使us与d轴同向,可以让us在q轴上的投影为0。当电网电压频率或相位突变时,us与d轴之间的夹角不再为0。为了使之为0,以达到锁相效果,可以采取措施使得θ=ω't。


1.2 DDSRF-SPLL 原理
根据对称分量法,可以将电网电压矢量us表述为正序分量、负序分量和零序分量的合成[8],即。同时可进一步将三相电压表示为:
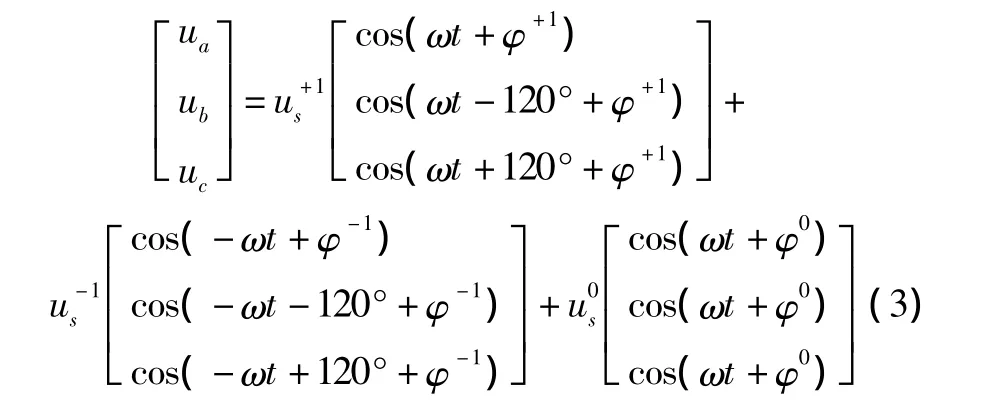
式中:φ+1、φ-1、φ0分别为正序、负序、零序基波电压的初始相位角。
将三相静止坐标系变换到两相静止坐标系后,可以得到α-β的坐标系:

计算得到零序分量在变换后为0,所以可以将式(4)进一步简化为式(5):
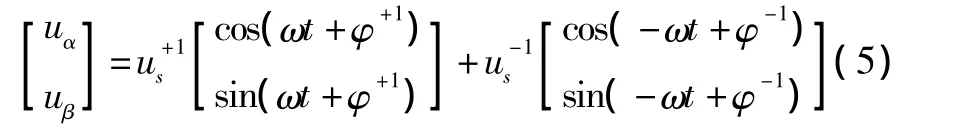
DDSRF-SPLL矢量图如图2所示。
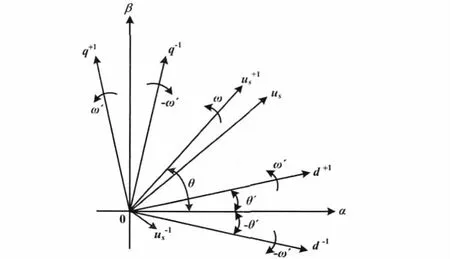
图2 DDSRF-SPLL矢量图Fig.2 Vector diagram of DDSRF-SPLL
图2显示了一个静止的坐标系和两个转动的坐标系。在α-β的坐标系上,电压矢量us可分解为以角频率ω旋转的正序电压分量和以角频率为-ω旋转的负序电压分量us-1组成,即两个分别以角频率ω和-ω旋转的坐标系 d+1-q+1以及坐标系 d-1-q-1,旋转过的角度分别为θ'、-θ'。通过对坐标系的旋转,使得两相静止坐标系转换为两相转动的坐标系。
根据单同步锁相环原理可知,当锁相环路锁相、us+1与正序分量d+1轴接近时,θ'≈θ。经过坐标系旋转,可以得到:

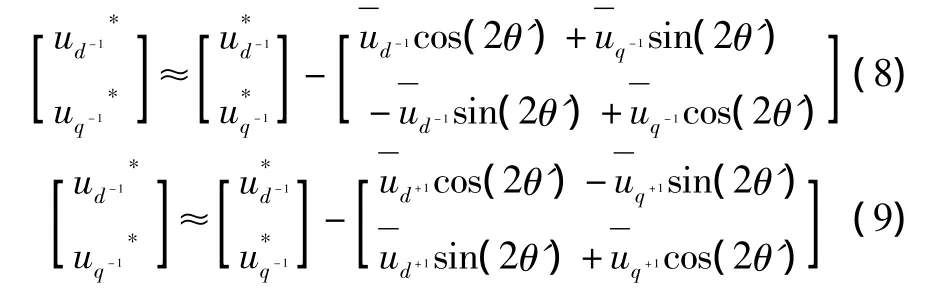
基于式(8)、式(9)构建的网络框图如图3所示。

图3 网络1示意图Fig.3 Schematic diagram of network 1
1.3 EPLL-SSRF-SPLL 原理
单同步坐标系软件锁相环在电压不稳定时表现很不理想,可以采取的方法是先将三相电压中的正序电压提取出来,从而消除负序电压对锁相环的影响,提升锁相环在不平衡电压条件下的锁频、锁相能力[9]。提取正序电压的转换矩阵如下:
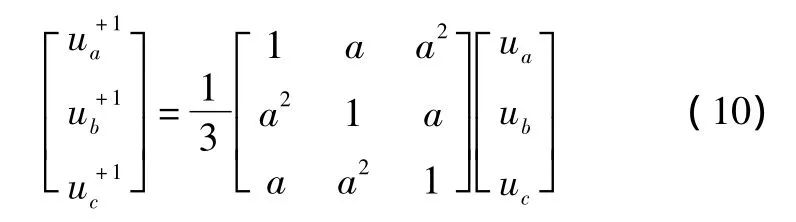
将a代入式(10)中,可以得到:
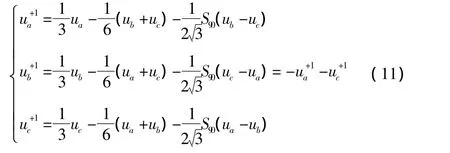
式中:S90为顺时针移动相位90°。
及时准确求取 ua、ub、uc,滤除各种干扰因素后的还原电压(锁相环输出电压)以及它们的正交向量S90ua、S90ub、S90uc显得尤为关键。
增强型锁相环(EPLL)由鉴相器、环路滤波器和压控振荡器等组成[10],用于求取各相电压还原电压及其正交分量的网络本身,其示意图如图4所示。使用这种增强型的锁相环路的目的就是能够对三相电压进行“过滤”,使其接近三相平衡电压的基波分量,从而增强锁相环的抗干扰性能。

图4 EPLL框图Fig.4 Block diagram of EPLL

2 电网电压检测仿真分析
2.1 电网电压理想
在电网正常的情况下,SSRF-SPLL、EPLL-SSRFSPLL与DDSRF-SPLL的频率和相位锁定曲线如图5所示。

图5 理想情况下频率、相位锁定曲线Fig.5 Frequency and phase lock under ideal conditions
锁相、锁频速度在很大程度上受到锁相环中PI环节参数的影响。本文通过设置相同的PI参数,使得三种锁相方法的滤波环节条件相同,这样便于达到对比的效果。其中,环路滤波器参数为Kp=10、Ki=802。
从图5可以看出,三种软件锁相方法均能快速锁定市电50 Hz的频率及其相位。由于DDSRF-SPLL使用了正负序解耦算法和低通滤波器环节,EPLL-SSRFSPLL中间嵌套了一个锁相环EPLL,导致三种方法锁相速度有所差异,其中SSRF-SPLL结构最简单、速度最快,DDSRF-SPLL次之,EPLL-SSRF-SPLL较慢。
2.2 单相电压跌落
电网故障中,电压跌落经常会对工业生产和生活用电造成很大的危害,现对单相电压跌落的情况进行仿真。假设A相短路跌落到0,B、C两相为正常电压311 V,则三种算法的锁频、锁相情况如图6所示。
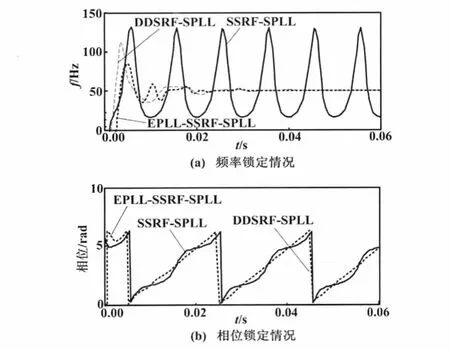
图6 单相电压跌落情况下频率、相位锁定对比Fig.6 Comparison of frequency and phase lock under single phase voltage dropping condition
从图6(a)可以看出,EPLL-SSRF-SPLL与DDSRFSPLL都能够迅速锁定频率,但SSRF-SPLL却发生了幅度较大的振荡,不能很好地锁定频率;从图6(b)可以看出,SSRF-SPLL相位锁定性能不佳,远不及能够迅速准确而锁定相位的EPLL-SSRF-SPLL与DDSRF-SPLL算法。
SSRF-SPLL、EPLL-SSRF-SPLL与 DDSRF-SPLL三种软件锁相方法在单相接地情况下的还原电压对电网A相的跟踪效果如图7所示。
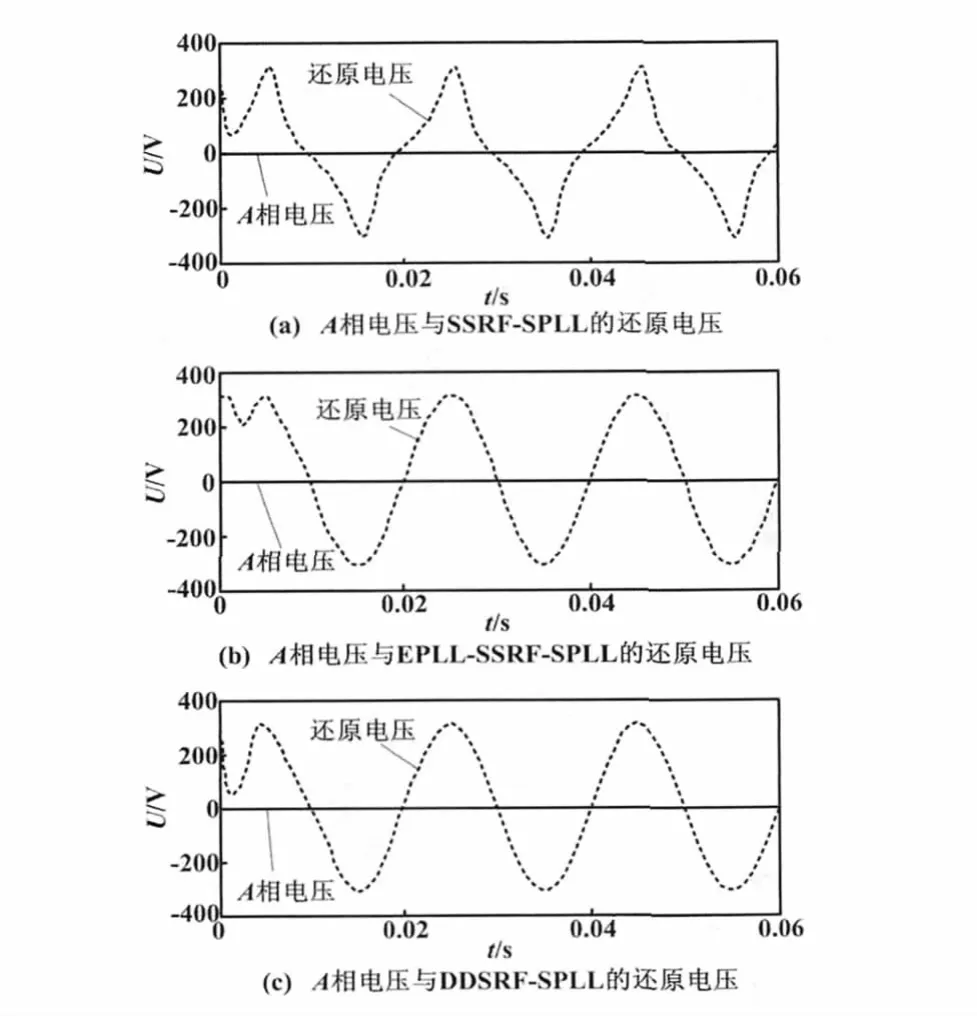
图7 在单相电压跌落情况下的电压还原效果Fig.7 Voltage recovery results under single phase voltage dropping condition
从图7可以看出,即便在A相电压为0 V的情况下,EPLL-SSRF-SPLL与DDSRF-SPLL也能够依据自己算法的优越性还原出A相电压,而SSRF-SPLL却不能做到较为准确的还原。
2.3 两相电压跌落
因三相电压不平衡而出现两相跌落的情况也很多见,仿真时假设A相电压正常(311 V)、B相跌落30%(218 V)、C相跌落50%(156 V)。对三种锁相算法锁频、锁相效果进行对比,对比结果如图8所示。
从图8(a)可以看出,EPLL-SSRF-SPLL与DDSRFSPLL都能够迅速锁定频率,但SSRF-SPLL却发生了幅度较大的振荡,不能锁定频率。同样,图8(b)中,SSRFSPLL相位出现抖动波动,而 EPLL-SSRF-SPLL与DDSRF-SPLL算法能够迅速准确地锁定相位。
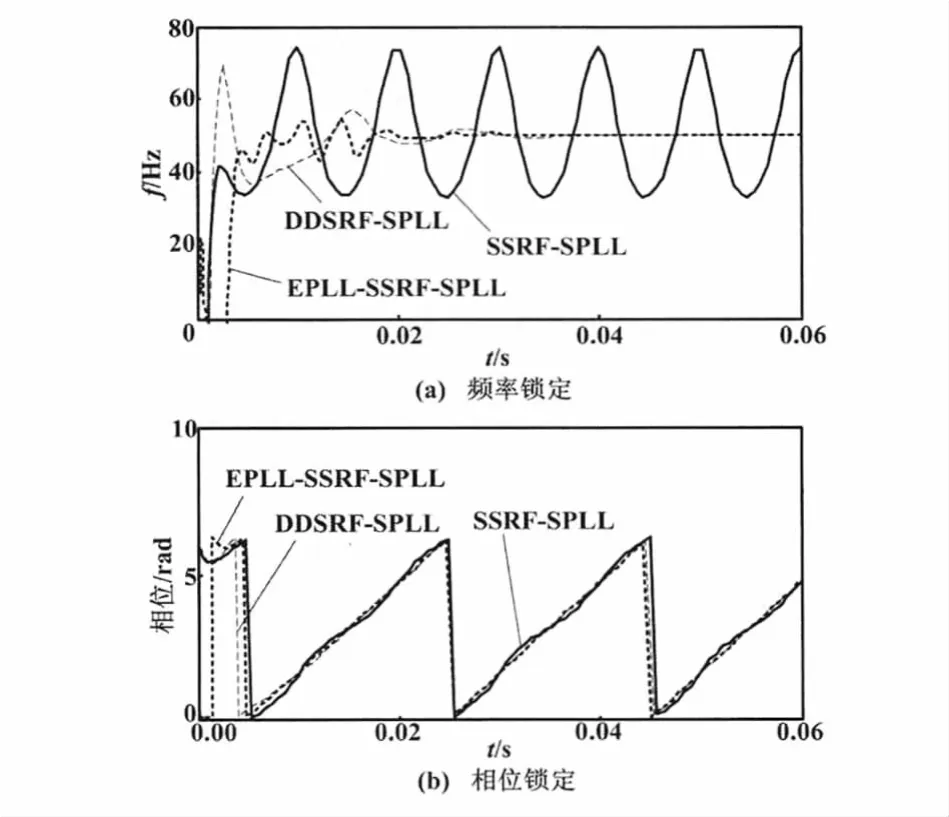
图8 两相电压跌落时频率、相位锁定情况Fig.8 Comparison of frequency and phase lock at two-phase voltage dropping
两相电压跌落时跟踪效果如图9所示。
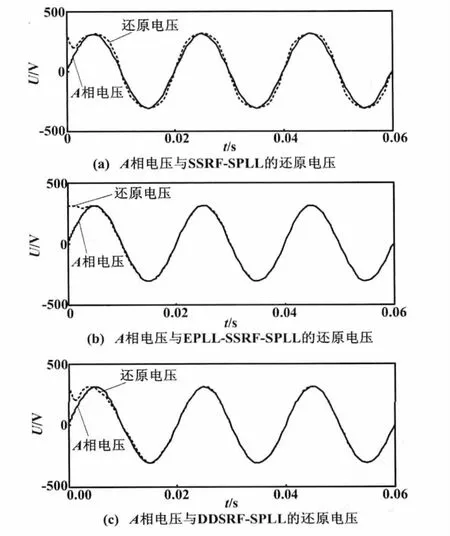
图9 两相电压跌落时跟踪效果对比Fig.9 Comparison of tracking results at two-phase voltage dropping
与图9(b)和9(c)中还原电压相比,图9(a)中还原电压虽然与A相电压比较接近,但在图9(a)中还原电压无法像图9(b)和9(c)一样很好地还原A相电压。这是由SSRF-SPLL频率和相位波动造成的。由此可以得出结论,在两相电压跌落情况下SSRF-SPLL锁相性能不佳。
2.4 频率突变
当频率在0.04~0.2 s发生突变(频率从50 Hz突减到40 Hz)时,SSRF-SPLL、EPLL-SSRF-SPLL与 DDSRFSPLL的锁频、锁相效果如图10所示。
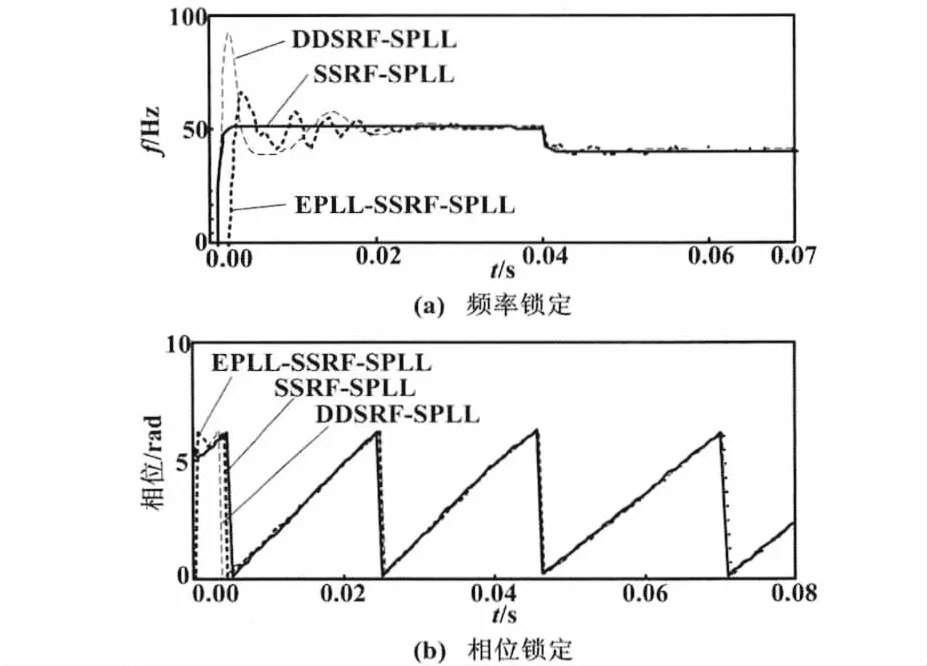
图10 频率突变情况下频率、相位锁定Fig.10 Frequency and phase lock at frequency mutation
从图10可以看出,三种方法在频率突变情况下频率和相位都能在较短时间内跟上相应电压,由于两个正弦函数(还原电压和A相电压)频率和相位相等,使得还原电压必定能跟上A相电压。
2.5 电压偏移
假设三相电压整体向上偏转30 V,频率和相位锁定情况如图11所示。
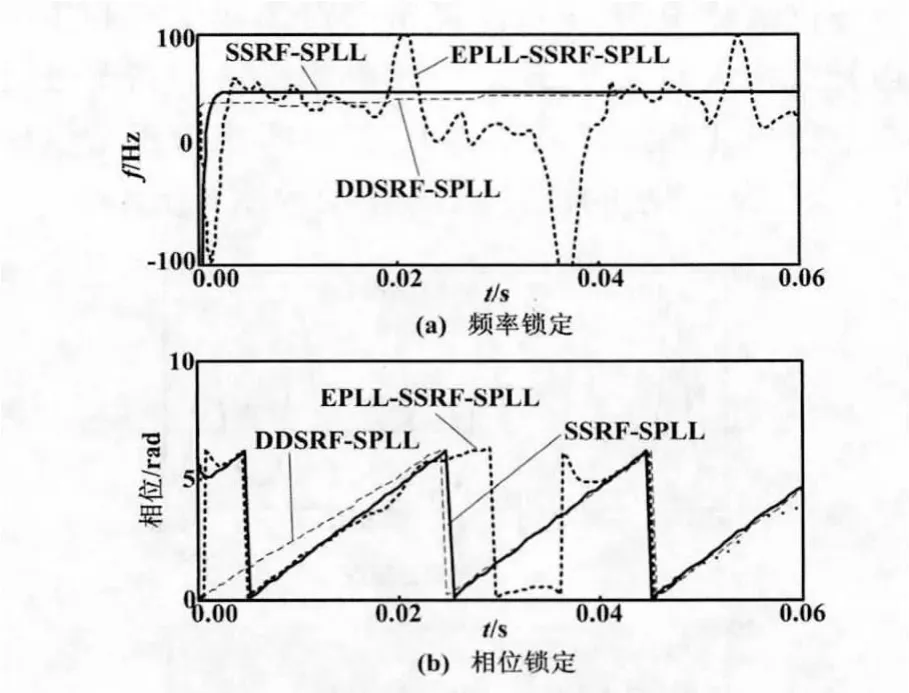
图11 电网电压偏转情况下频率、相位锁定对比Fig.11 Comparison of frequency and phase lock at grid voltage deflection
由图11可以看出,SSRF-SPLL和DDSRF-SPLL能够在这种情况下迅速实现频率和相位的锁定,而EPLL-SSRF-SPLL却不能有效并快速地锁定。
SSRF-SPLL、EPLL-SSRF-SPLL、DDSRF-SPLL 三种软件锁相方法在电压偏转情况下的还原电压对电网A相的跟踪效果如图12所示。
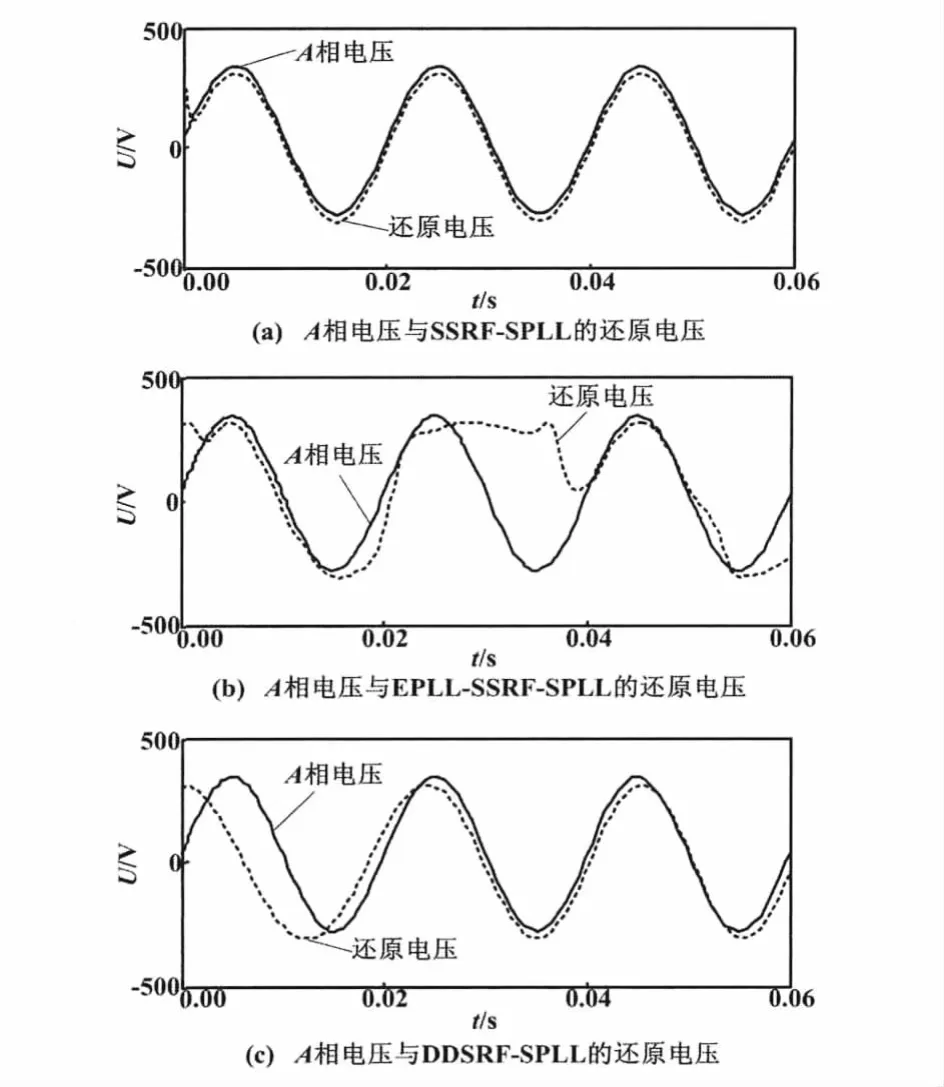
图12 电压偏转情况下跟踪效果Fig.12 The tracking results at voltage deflection
由图12可以看出,EPLL-SSRF-SPLL不能有效地跟踪电网电压,而SSRF-SPLL和DDSRF-SPLL却能较好地锁定电网频率和相位。
3 结束语
本文简述了单同步坐标系软件锁相环、双同步坐标系软件锁相环以及增强型软件锁相环的基本原理,并通过所建立的仿真模型,分析对比了三种锁相环的电网监测能力。
当三相电压平衡时,三种锁相环都能够锁相,在相同的PI参数条件下,单同步坐标系软件锁相环锁相最快。单同步坐标系软件锁相环在正序电压检测性能方面表现很好,速度也很快。但当含有负序分量的情况如电网电压单相短路、双相跌落及谐波注入时,单同步坐标系软件锁相环不能准确锁相;而当电压发生偏移时,双同步坐标系软件锁相环要比增强型软件锁相环效果好。双同步坐标系软件锁相环对各种不同电压状况的适应能力要更强些,并能够较准确且较快速地实现电压频率相位的跟踪监测。
[1]李波,姬劳.基于FPGA的三相电压过零点高精度检测[J].低压电器,2006(6):51 -55.
[2]郭雨梅,周晓章,陈曦.基于FPGA的新型数字锁相倍频方法[J].仪表技术与传感器,2010(5):60-62.
[3] Chung S.A phase tracking system for three phase utility interface inverters[J].IEEE Transactions on Power Electronics,2000,15(3):431-438.
[4] Pedro R,Josep P,Joan B.Decoupled double synchronous reference frame PLL for power converters control[J].IEEE Transactions on Power Electronics,2007,22(2):584 -592.
[5]田桂珍,王生铁,林百娟.基于d-q变换的改进型锁相环设计[J].内蒙古工业大学学报:自然科学版,2009,28(1):64-68.
[6]张治俊,李辉,张煦,等.基于单/双同步坐标系的软件锁相环建模和仿真[J].电力系统保护与控制,2011,39(11):138 -144.
[7]周鹏,贺益康,胡家兵.电网不平衡状态下风电机组运行控制中电压同步信号的检测[J].电工技术学报,2008,23(5):108 -113.
[8]田桂珍,王生铁,林百娟,等.电压不平衡时风电系统中基于双同步变换的锁相环设计[J].电气传动,2010,40(7):53 -57.
[9]张煦,周小铃,王亚飞,等.电网电压非理想工况下的软件锁相环比较与研究[C]//重庆市电机工程学会2010年学术会议,2010:845-850.
[10]徐健飞,庞浩,王赞基,等.新型全数字锁相环的逻辑电路设计[J].电网技术,2006,30(13):81-84.

