多尺度排列熵及其在滚动轴承故障诊断中的应用

郑近德 程军圣 杨 宇

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

时频分析方法由于能够提供振动信号时域和频域局部信息而在故障诊断领域得到了广泛应用，是目前故障诊断的重要手段［1－2］。该方法通过对信号进行小波分析［3］或经验模态分解［4－5］，将非平稳信号分解为若干个简单的平稳信号之和，然后对每个分量进行处理，提取时频域信息，进而得到原始信号的完整时频信息。然而，由于机械运转过程中的摩擦、振动以及负载等因素，机械系统振动信号往往表现出非线性行为，采用时频分析的方法，将信号分解为平稳信号，难免有一定的局限性。非线性分析的方法可以不经过对原始信号分解，而能够直接提取隐藏在机械系统振动信号中其他方法无法提取的故障信息［6］。

近年来，越来越多的非线性分析方法被用于机械故障诊断，如关联维数、近似熵、样本熵、多尺度熵等。徐玉秀等［7］研究了旋转机械的分形特征及故障诊断，Yan等［8］将近似熵应用于机械系统健康状态监测，Zhang等［9］将多尺度熵应用于滚动轴承的故障诊断。然而，分形维数的计算依赖数据长度，且较耗时，不适合在线监测；近似熵相对一致性较差［9］；多尺度熵［10－11］是基于样本熵而定义的，计算较耗时，且受时间序列的非平稳性和异常值的影响。

排列熵［12］是一种新的随机性和动力学突变的检测方法，它具有计算简单，抗噪能力强，且得到较稳定的系统特征值所需时间序列短，适合在线监测等优点，在肌电信号处理［13］、心率信号处理［14］、气温复杂度［15］等方面都取得了良好的效果。Yan等［6］将其应用于旋转机械振动信号的特征提取，并将其与近似熵和Lempel－Ziv复杂度进行了对比，结果表明，排列熵能够有效地检测和放大振动信号的动态变化，并且能够表征滚动轴承在不同状态下的工况特征。然而，与传统的基于单一尺度分析的非线性参数类似，排列熵只是检测时间序列在单一尺度上的随机性和动力学突变。Aziz等［16］提出了多尺度排列熵（multiscale permutation entropy，MPE）的概念，用于衡量时间序列在不同尺度下的复杂性和随机性，并通过分析生理信号，将其与多尺度熵进行了对比，结果表明，相对于多尺度熵，MPE更具有鲁棒性。由于机械系统比较复杂，振动信号不仅在单一尺度上包含有重要信息，而且在其他尺度上也包含有重要信息，因此，对振动信号进行多尺度分析是一种有效的方法。

本文将MPE引入到机械故障诊断领域，应用于滚动轴承的故障特征的提取。由于正常滚动轴承的振动信号是随机振动信号，而当滚动轴承发生故障时，振动信号随机性和动力学行为会发生变化。因此，本文考虑用MPE来衡量振动信号的随机性变化和动力学突变，并将MPE值作为特征参数，提取滚动轴承的故障特征。在此基础上，结合支持向量机（support vector mechine，SVM）［17－18］作为模式识别分类，提出一种基于MPE和SVM的滚动轴承故障诊断方法，并将其应用于滚动轴承实验数据的分析，结果表明，新提出的方法能够有效地诊断滚动轴承的故障类型。

1 排列熵及多尺度排列熵原理和算法

1.1 排列熵算法

排列熵的原理在于不考虑数据具体值，而是基于相邻数据的对比。下面说明其计算方法。

考虑长度为N 的时间序列｛x（i），i＝1，2，…，N｝，对其进行相空间重构，得到如下的时间序列：

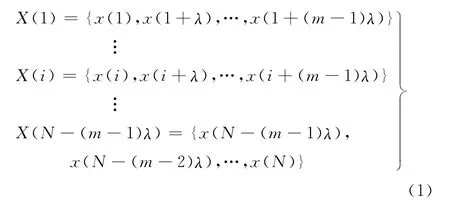
式中，m为嵌入维数；λ为时延。

将X（i）的m个数据按照升序重新排列，即

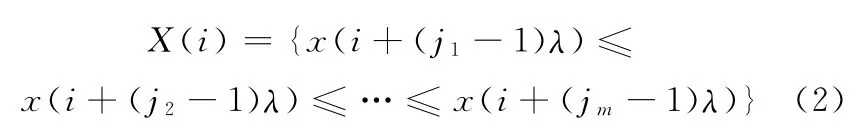
如果存在x（i＋ （ji1－1）λ）＝x（i＋ （ji2－1）λ），此时按j值的大小来进行排序，即当jk1＜jk2，有x（i＋（ji1－1）λ）≤x（i＋（ji2－1）λ），所以，任意一个数据X（i）都可以得到一组符号序列：

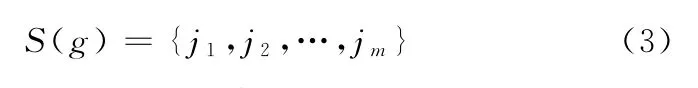
其中，g ＝1，2，…，k，k ≤ m！，m 个不同的符号｛j1，j2，…，jm｝共有m！种不同的排列，对应地，共有m！种不同的符号序列，S（g）是m！种符号序列中的一种。计算每一种符号序列出现的概率＝1，此时，时间序列｛x（i），i＝1，2，…，N｝的排列熵就可以按照Shannon熵的形式定义为

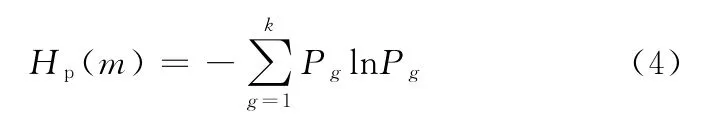
注意到，当Pg＝1／m！时，Hp（m）达到最大值ln（m！），因此，可以通过ln（m！）将排列熵Hp（m）进行标准化处理，即

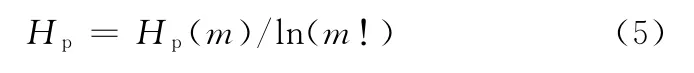
显然，Hp的取值范围是0≤Hp≤1。Hp值的大小表示时间序列的复杂和随机程度。Hp越大，说明时间序列越随机，反之，则说明时间序列越规则。Hp值的变化反映和放大了时间序列的局部细微变化。

1.2 排列熵参数的选取

在排列熵的计算中，有3个参数值需要考虑和设定，即时间序列长度N、嵌入维数m和时延λ。Bandt等［12］建议嵌入维数m取3～7，因为如果m等于1或2，此时重构的序列中包含太少的状态，算法失去意义和有效性，不能检测时间序列的动力学突变。但是，如果m取值过大，也不合适，因为相空间的重构将会均匀化时间序列，此时不仅计算比较耗时，而且也无法反映序列的细微变化［8，15］。

为研究数据长度N对排列熵值的影响，以长度分别为128、256、512、1024和2048的高斯白噪声信号为例，求得对应排列熵值，分别记为PE1～PE5，如图1所示，它们在不同嵌入维数下差值如表1所示。

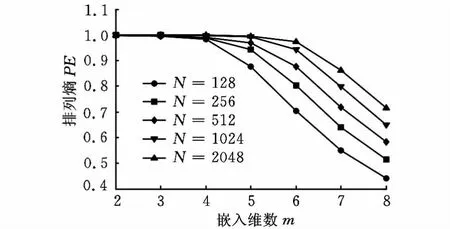
图1 不同长度的高斯白噪声的排列熵

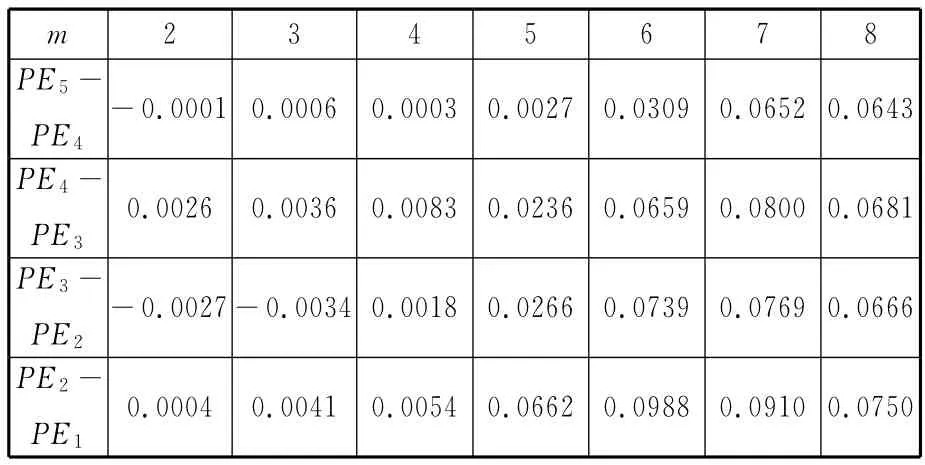
表1 不同长度高斯白噪声信号排列熵在不同嵌入维数下的差值

由图1和表1可以发现，以嵌入维数m＝6为例，数据长度分别为1024和512时，熵值相差0.0659，而数据长度分别为2048和1024时，则熵值仅相差0.0309，因此，此时选数据长度为1024较合适。而对m＝5而言，数据长度分别为1024和256的信号的熵值仅相差0.0502，此时，数据长度为256已经可以估计合理的排列熵值。一般，嵌入维数较小时，数据长度则要求越小。

时延λ对时间序列的计算影响较小，以长度为512的高斯白噪声信号为例，在不同λ下的排列熵值随嵌入维数的变化关系如图2所示，由图可以看出，时延对信号熵值的影响较小，因此，本文取λ＝1。

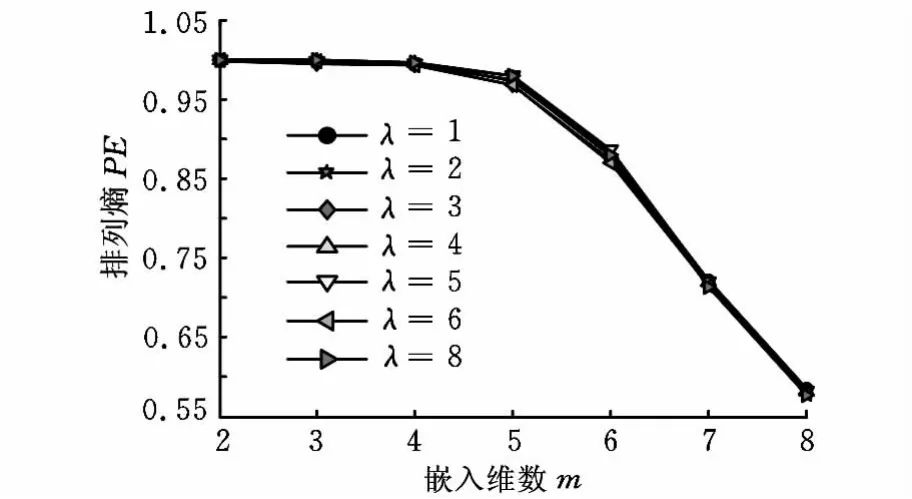
图2 高斯白噪声信号在不同时延下的排列熵

1.3 多尺度排列熵定义

多尺度排列熵定义为不同尺度下的排列熵，计算方法如下：

（1）考虑时间序列｛x（i），i＝1，2，…，N｝，对其进行粗粒化处理，得到粗粒化序列的表达式为

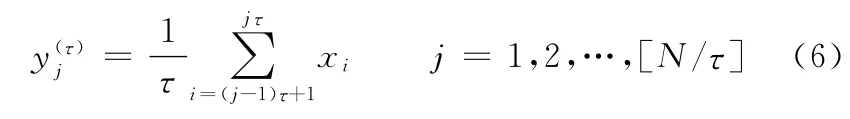
其中，［N／τ］表示对N／τ取整；τ为尺度因子，τ＝1，2，…。显然τ＝1，粗粒化序列即为原始序列；τ＞1时，原始序列被粗粒化为长度为［N／τ］的粗粒序列。

（2）计算每个粗粒序列的排列熵，并画成尺度因子的函数，上述过程即称为多尺度排列熵分析。

尺度因子的最大值一般取大于10即可，但要保证粗粒化序列长度［N／τ］不影响熵值的计算。

为了选取合适的计算MPE的嵌入维数，仍以高斯白噪声为例，数据长度为2048，尺度因子最大值为12，λ＝1，在m 分别为4、5、6和7时，求得它们的MPE，相对耗时分别为0.1880s、0.6710s、3.8290s和27.6710s，将MPE画成尺度因子的函数，如图3所示。

由图3可以看出，若m 取值太小，则PE值随尺度因子的增大而减小，但m越大，计算越耗时，因此，本文选取m＝6。此外，由图3可以看出，高斯白噪声的MPE随着尺度因子的增大而单调递减，这说明白噪声只在最小尺度上包含有主要信息。

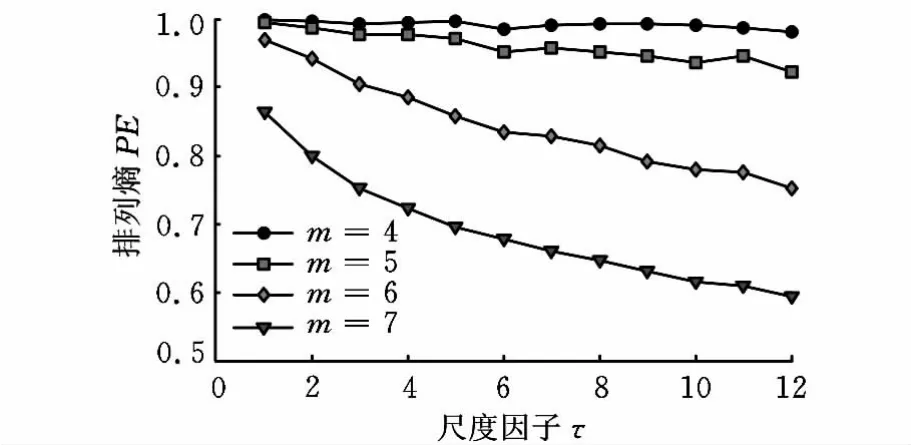
图3 高斯白噪声在不同嵌入维数下的MPE

2 基于MFE的滚动轴承故障诊断方法及应用

在上述理论的基础上，本文提出基于MPE和SVM的滚动轴承故障诊断方法。首先，从滚动轴承的原始振动信号从提取MPE；其次，依据MPE提取合适的故障特征向量；第三，采用SVM进行故障分类，从而实现滚动轴承故障类别的诊断。

为了说明本文方法的有效性，本文将该方法应用于实验数据分析。本文实验数据采用Case Western Reserve University（CWRU）轴承数据中心提供的滚动轴承试验数据［9］。测试轴承为6205－2RS JEM SKF深沟球轴承，电机功率约为2206.4963W，转速为1730r／min，采用电火花加工技术在轴承上布置单点故障，故障直径为0.5334mm，深度为0.2794mm。在此情况下采集到正常（normal，简称 NORM）、内圈故障（inner race fault，IRF）、外圈故障（outer race fault，ORF）和滚动体故障（rolling element fault，REF）4种状态的振动信号，各30组数据，数据长度为2048，采样频率为12kHz，4种状态轴承的振动信号时域波形如图4所示。

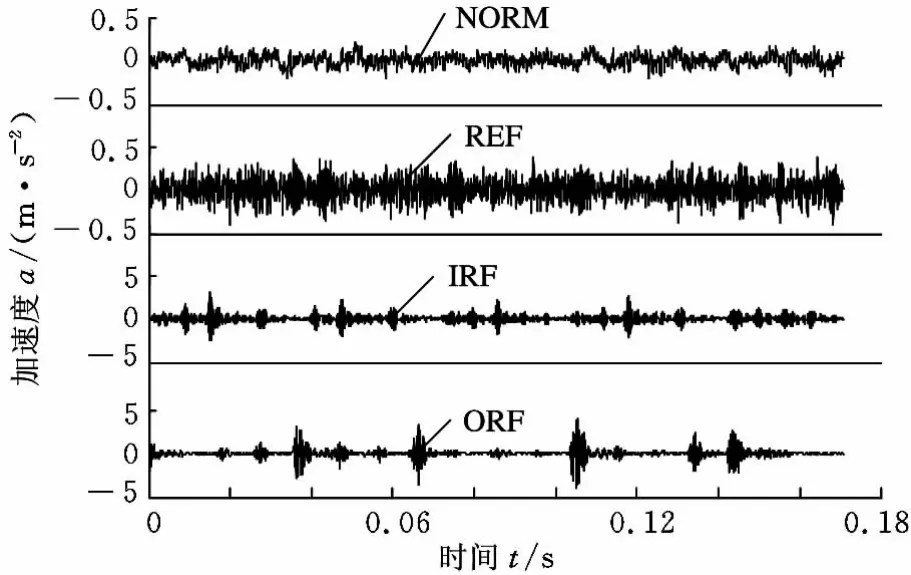
图4 正常和不同故障轴承振动信号的时域波形

从图4不易发现正常和故障轴承振动信号的明显区别，尤其是正常和滚动体故障，以及内圈故障和外圈故障。因此，本文首先对振动信号进行MPE分析，取嵌入维数m＝6，时延λ＝1，最大尺度因子为12，4种状态滚动轴承的多尺度排列熵画成尺度因子的函数，如图5所示。

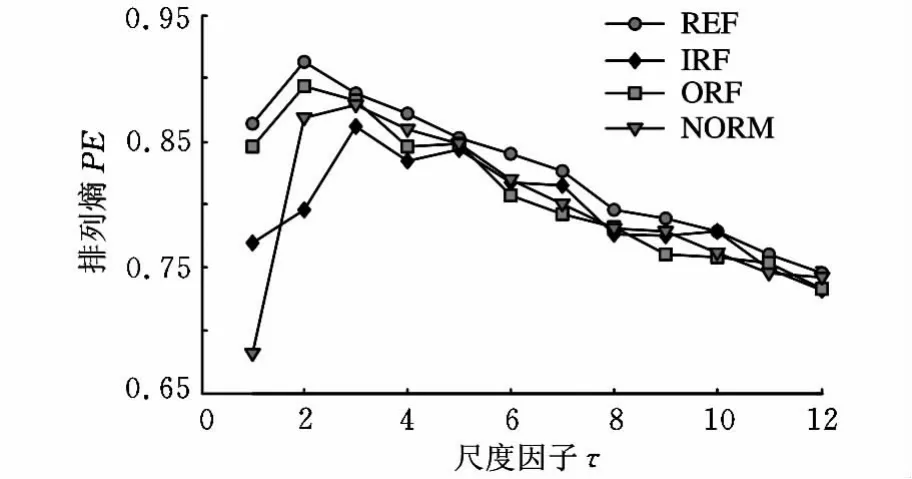
图5 正常和故障滚动轴承振动信号的多尺度排列熵

在尺度因子等于1时，即为原始振动信号的排列熵，由于熵值比较接近，无法明显地区别三种故障和正常轴承的类型，因此有必要对振动信号进行多尺度分析。为此，以多尺度排列熵值为特征参数，同时建立基于SVM的分类器，进行训练和测试。如果采用全部的12个特征值进行训练，会造成信息的冗余，且训练比较耗时，也需要较多的训练样本，且由图5也可以看出，前几个尺度的熵值表征了振动信号的主要信息，因此，采用前4个尺度的排列熵值作为特征向量，即T＝（PE1，PE2，PE3，PE4）。因此，本文的方法如下：

首先，提取特征参数，即对振动信号进行MPE分析，提取特征参数T。正常、滚动体故障、内圈故障和外圈故障4种状态，每种状态取30个样本，故每种状态可得到30个表征故障特征的特征向量，共得到120个特征向量。

其次，训练分类器。由于有3种故障状态和正常状态，因此，需建立3个SVM，其中SVM1为正常对3种故障分类器，SVM2为内圈故障对滚动体和外圈故障分类器，SVM3为滚动体故障和外圈故障分类器。每种状态随机抽取10个样本进行训练，并将每组30个样本用来测试。经过训练，SVM1和SVM3采用径向基核函数，SVM2采用多项式核函数。基于SVM的多故障分类器如图6所示。

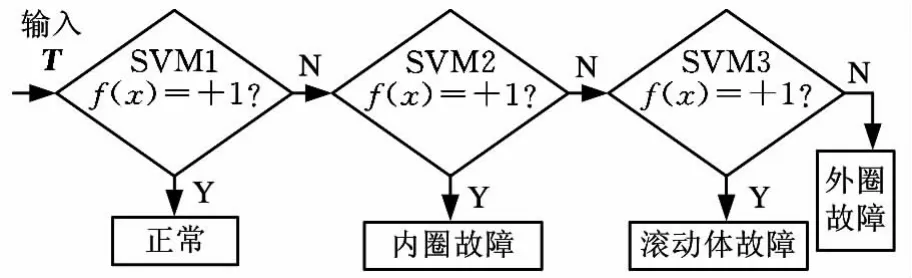
图6 多类故障支持向量机分类器示意图

最后，测试分类器。对已训练的SVM1、SVM2和SVM3，用全部样本进行测试，详细测试样本输出结果如表2所示。

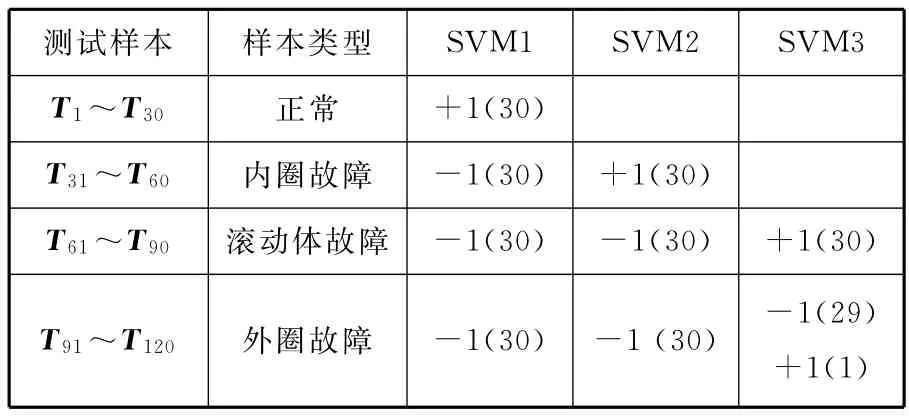
表2 测试样本SVM分类器的输出结果

由表2可以看出，本文提出的方法有很好的效果，在全部样本用来测试中，只有一组外圈故障的样本被错分为滚动体故障，其他都得到了正确的分类，正确识别率为99.17%。为了比较，下面建立以 BP 神 经 网 络 为 基 础 的 多 分 类 器［9，19－20］，BP分类器除输入层外，第一层隐含层有8个节点，第二层输出层有4个节点。为表述方便，标记正常为1类，内圈故障为2类，滚动体为3类，外圈故障为4类。BP分类器的训练和测试样本与支持向量机相同，其分类结果如图7所示。

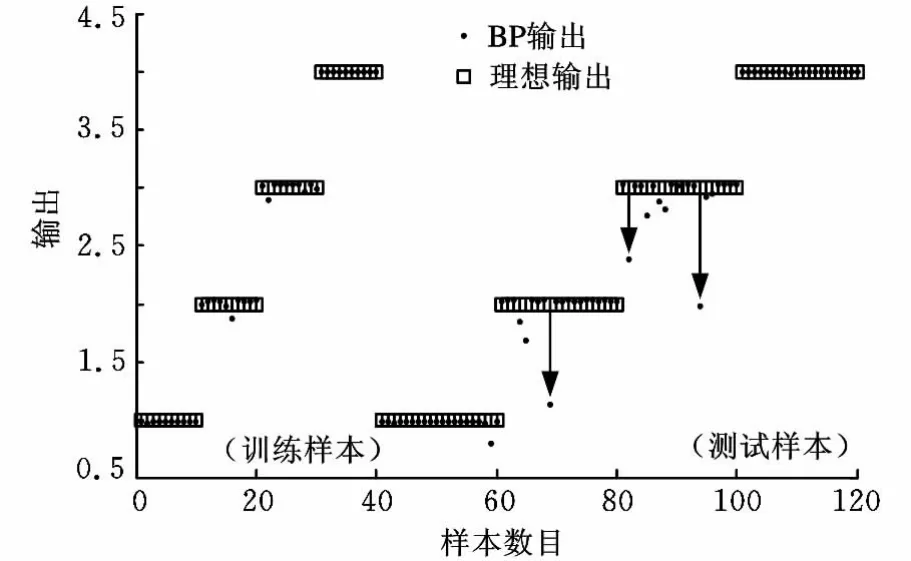
图7 BP神经网络分类器输出结果

图7中，训练样本作测试时，全部分类正确，而测试样本作测试时有3组分类错误，准确率为97.5%。这说明支持向量机的分类效果要优于BP神经网络。而且，在训练时间上，支持向量机也比BP神经网络短得多。

为了说明进行多尺度分析的必要性，下面选取尺度因子等于1时（即原始信号）的排列熵值作为特征参数，分别通过SVM和BP神经网络分类器进行训练和测试。其中，SVM分类器中，有6组样本分类错误，如表3所示；而BP神经网络分类器也有6组样本分类错误，如图8所示。

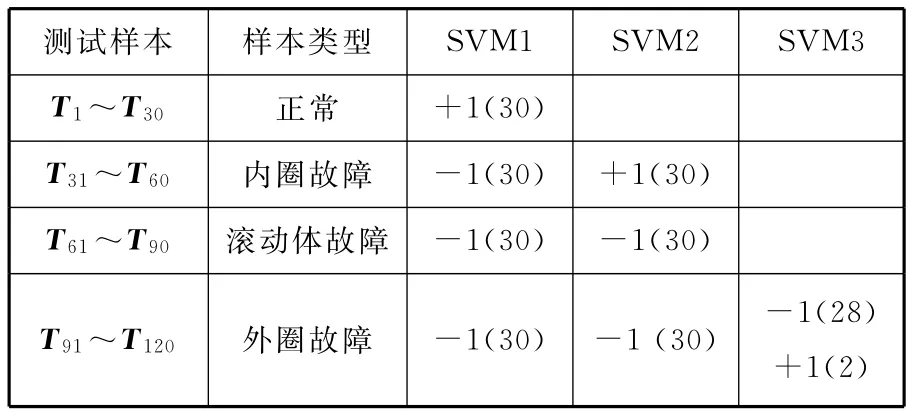
表3 测试样本SVM分类器的输出结果

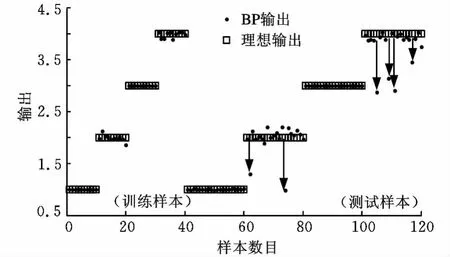
图8 BP神经网络分类器输出结果

从上文可以看出，原始信号单一尺度的排列熵作为特征参数，分类效果不理想，这说明了单一尺度上原始振动信号的排列熵并不能反映故障的本质，而多个尺度上的排列熵值则能够更好地实现分类。另外易发现，特征值的选取对分类结果的影响尤为关键。本文选取特征值为前4个尺度上的特征值，主要基于以下原因考虑：如果特征值过少，不能完全反映故障的特征信息，而特征值过多会造成信息冗余，且需要增加训练样本和训练时间，因此，本文选取了前4个尺度上的特征值。文献［9］中选择多尺度熵值的统计量时，将最大值、最小值、代数平均、几何平均和标准差作为特征向量，但统计量方法忽略了特征值之间的内在关系，因此，采用前4个尺度因子的排列熵值作为特征参数。

3 结束语

机械系统发生故障时，振动信号会在不同尺度上表现出不同程度的随机性和动力学突变，基于此，本文提出了一种新的基于多尺度排列熵和支持向量机的滚动轴承故障诊断方法，并将支持向量机与BP神经网络分类效果进行了对比。结果表明，支持向量机在训练时间和准确率方面，都优于BP神经网络。此外，本文还将特征向量包含多个尺度上熵值与特征向量仅包含原始信号单一尺度上排列熵值进行了对比，结果表明，原始信号单一尺度上排列熵值的不能全部反映故障的本质，而多尺度的排列熵值则有很好的诊断效果。本文提出的方法为故障诊断提供了一种新的思路和手段。

［1］于德介，程军圣，杨宇.机械故障诊断的 Hilbert－Huang变换方法［M］.北京：科学出版社，2007.

［2］何正嘉，陈进，王太勇，等.机械故障诊断理论及应用［M］.北京：高等教育出版社，2010.

［3］程军圣，于德介，邓乾旺，等.连续小波变换在滚动轴承故障诊断中的应用［J］.中国机械工程，2003，14（23）：2037－2040.Cheng Junsheng，Yu Dejie，Deng Qianwang，et al.Rolling Bearing Fault Diagnosis Using Continuous Wavelet Transform［J］.China Mechanical Engineering，2003，14（23）：2037－2040.

［4］Huang N E，Wu Z.A Review on Hilbert－Huang Transform：Method and Its Applications to Geophysical Studies［J］.Advances in Adaptive Data Analysis，2009，1：1－23.

［5］Yu Dejie，Cheng Junsheng，Yang Yu.Application of EMD Method and Hilbert Spectrum to the Fault Diagnosis of Roller Bearings［J］.Mechanical Systems and Signal Processing，2005，19：259－270.

［6］Yan Ruqiang，Liu Yongbin，Gao R X.Permutation Entropy：A Nonlinear Statistical Measure for Status Characterization of Rotary Machines［J］.Mechanical Systems and Signal Processing，2012，29：474－484.

［7］徐玉秀，钟建军，闻邦椿.旋转机械动态特性的分形特征及故障诊断［J］.机械工程学报，2005，41（12）：186－189.Xu Yuxiu，Zhong Jianjun，Wen Bangchun.Fractal Fault Diagnosis and Classification to Modal Characteristic of Rotor System［J］.Journal of Chinese Mechanical Engineering，2005，41（12）：186－189.

［8］Yan Ruqiang，Gao R X.Approximate Entropy as a Diagnostic Tool for Machine Health Monitoring［J］.Mech.Syst.Signal Process，2007，21：824－839.

［9］Zhang Long，Xiong Guoliang，Liu Hesheng.Bearing Fault Diagnosis Using Multi－scale Entropy and Adaptive Neuro－fuzzy Inference［J］.Expert Systems with Applications，2010，37：6077－6085.

［10］Richman J S，Moorman J R.Physiological Timeseries Analysis Using Approximate Entropy and Sample Entropy［J］.American Journal of Physiology－Heart and Circulatory Physiology，2000，278：2039－2049.

［11］Costa M，Goldberger A L，Peng C K.Multiscale Entropy Analysis of Physiologic Time Series［J］.Physical Review Letters，The American Physiological Society，2002：068102（1－4）.

［12］Bandt C，Pompe B.Permutation Entropy：a Natural Complexity Measure for Time Series［J］.Physical Review Letters，The American Physiological Society，2002：174102（1－4）.

［13］袁明，罗志增.基于排列组合熵的表面肌电信号特征分析［J］.杭州电子科技大学学报，2012，32（1）：64－67.Yuan Ming，Luo Zhizeng.Feature Analysis of SEMG Based on Permutation Entropy［J］.Journalof Hangzhou Dianzi University，2012，32（1）：64－67.

［14］马千里，卞春华.改进排列熵方法及其在心率变异复杂度分析中的应用［J］.中国组织工程研究与临床康复，2010，52（14）：9781－9785.Ma Qianli，Bian Chunhua.Application of Modified Permutation Entropy in Heart Rate Variability Analysis［J］.Journal of Clinical Rehabilitative Tissue Engineering Research，2010，52（14）：9781－9785.

［15］侯威，封国林，董文杰，等.利用排列熵检测近40年华北地区气温突变的研究［J］.物理学报，2006，55（55）：2663－2668.Hou Wei，Feng Guolin，Dong Wenjie，et al.A Technique for Distinguishing Dynamical Species in the Temperature Time Series of North China［J］.Acta Physica Sinica，2006，55（55）：2663－2668.

［16］Aziz W，Arif M.Multiscale Permutation Entropy of Physiological Time Series［C］／／Proceeding of IEEE International Multi－topic Conference，INMIC，2005.

［17］李岳，陶利民，温熙森.用于滚动轴承故障检测与分类的支持向量机方法［J］.中国机械工程，2005，16（6）：498－501.Li Yue，Tao Limin，Wen Xisen.Support Vector Machines Based Approach for Ball Bearing Fault Detection and Classification［J］.China Mechanical Engineering，2005，16（6）：498－501.

［18］Yang Yu，Yu Dejie，Cheng Junsheng.A Fault Diagnosis Approach for Roller Bearing Based on IMF Envelope Spectrum and SVM［J］.Measurement，2007，40：943－950.

［19］李永强，刘杰，侯祥林，等.人工神经网络的混合算法及其工程应用［J］.机械工程学报，2004，40（1）：127－130.Li Yongqiang，Liu Jie，Hou Xianglin，et al.Mixed Method of Artificial Neural Network and Its Application on Fault Diagnosis for Rotational Machine［J］.Journal of Chinese Mechanical Engineering，2004，40（1）：127－130.

［20］飞思科技产品研发中心.神经网络理论与 MATLAB7实现［M］.北京：电子工业出版社，2005.