基于弹性稳定约束的桁架臂顶节铰点布局优化研究
王 欣 王成林 周 杨 徐金帅
1.大连理工大学,大连,116023 2.大连益利亚工程机械有限公司,大连,116024
0 引言
桁架臂顶节铰点布局问题,是桁架类吊臂方案设计的关键问题之一。其设计是否合理,直接关系到桁架吊臂的受力是否合理[1]和整体的抗屈曲能力大小,进而影响桁架类起重机整机的起重性能。
目前,对桁架臂结构优化分析的方法主要有以下三种:一是采用解析法[2]计算吊臂的强度及稳定性,然后对计算结果进行筛选取优;二是运用有限单元法对桁架类结构进行尺寸及形状优化[3];三是运用ANSYS对空间桁架结构进行拓扑优化设计[4]。这几种方法对桁架臂结构的研究发挥了一定的作用,但均存在诸多不足:①桁架类臂架结构复杂且工况繁多,很难通过解析法获得最优化的结构形式;②有限元参数化建模困难,优化过程繁琐,耗费大量计算成本;③拓扑优化思想真正应用于工程实际尚有一定的距离,只停留在研究探索阶段。
再者,结构铰点优化这类多变量优化设计问题,是传统设计方法难以求解的问题之一[5-6]。文献[7]通过运用遗传算法,对结构工作装置铰点位置进行了优化,但又仅局限于该特定结构铰点形式的求解,对于桁架臂顶节铰点优化问题,该方法不能完全适用。
铁摩辛柯弹性梁理论[8]是工程实际中求解实心柱、组合柱以及“格子”柱压弯稳定性问题的经典理论之一,广泛运用于轴向压弯臂架结构的稳定性计算与分析。轴心压弯构件在横向载荷及端部集中弯矩下将产生初始变形,轴向力除有压缩作用外还将产生附件弯矩使构件产生更大变形,工程上称之为“二次压弯效应”,而这种现象在工程实际与研究中往往不应该被忽略。因此,本文以铁摩辛柯弹性梁理论为依据建立优化模型。
桁架臂顶节铰点优化问题是多变量、多极值点的约束非线性规划问题,常规的优化方法不易得到最优解。遗传算法[9-11]具有全局寻优的能力,能够解决复杂的优化设计问题,在结构分析领域中的应用越来越广泛。基于此,本文从工程实际出发,以桁架臂顶节铰点位置为优化变量,以各铰点坐标值上下边界及两铰点不产生干涉最小距离为约束条件,以最小屈曲储存应变能为目标函数建立数学模型,在MATLAB环境下编制了优化分析程序,运用改进的遗传算法对优化问题进行求解。
1 结构铰点布局优化模型的建立
桁架臂顶节铰点布局设计中,铰点的合理布置可以改善桁架臂结构在起吊重物过程中的受力性能,降低挠度,提高整体稳定性。
桁架臂铰点布局优化的关键是从工程复杂设计问题中抽象建立起合理的优化数学模型。优化数学模型的建立,不仅要考虑工程实际中各铰点上各部件的安装状态,避免干涉,还应考虑整个顶节的运输尺寸的要求。在此基础上,还要寻找适合该问题的合理的目标函数。
1.1 桁架臂主要载荷的确定
桁架式吊臂采用动定滑轮实现重物升降动作。作用在桁架臂上的载荷主要有起升载荷、自重、拉索力以及风载荷等。桁架臂自重可视为沿桁架臂长度方向均匀分布,按力矩平衡原理,也可认为按重心位置分配至桁架臂根部铰点和顶端,本文计算时采用后者。图1所示为桁架臂受力状态,其中,e1为桁架臂轴线到起升绳导向滑轮中心的距离(拉索铰点与升绳导向滑轮中心重合);e2为桁架臂轴线到起升定滑轮中心的距离;θ为桁架臂仰角;θ1为拉索与桁架臂轴线的夹角;θ2为起升钢丝绳与桁架臂轴线的夹角;Q为起重量;T1为拉索拉力;T2为起升绳拉力。
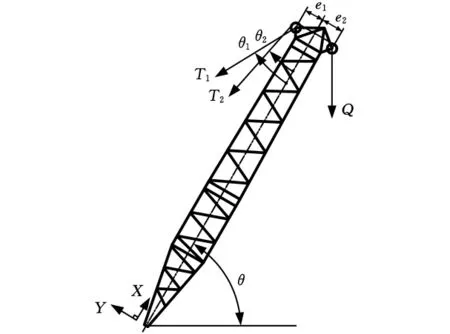
图1 桁架臂受力简图
垂直方向载荷Q0为
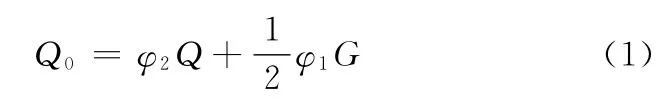
式中,φ1为自重冲击系数;φ2为起升动载系数;G为吊臂自重。
桁架臂轴向载荷S为
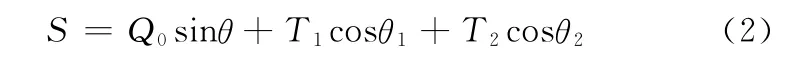
变幅平面内端部弯矩M0为
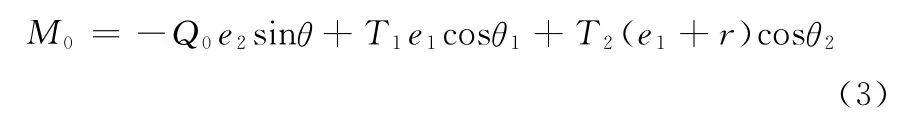
式中,r为导向滑轮半径。
由以上受力分析可知,起重桁架臂是以受压为主的轴向压弯构件。理想情况下,桁架臂在顶节处仅受轴向载荷,但实际情况下,需要考虑部件的安装空间、工艺等要求,各铰点位置不能重合于臂架轴线上,因此必然引起附加的弯矩。而合理布置铰点位置,可最大限度地减小这种附加弯矩,从而改善臂架受力。
1.2 桁架臂结构截面惯性矩计算
对于图1所示的桁架臂臂架结构,需要计算其任意截面惯性矩,才能进行力学模型的简化,其简化方法如下:
对于不同结构形式的臂架结构(图2),任意截面m-n惯性矩可由下式求得:

式中,I1为杆顶端截面惯性矩;n为与形状有关的常数,对于图2c所示的结果取n=2。
1.3 桁架臂力学模型简化
如图3所示,在变幅平面内(桁架臂绕根部铰点转动的平面),将桁架臂模型简化成简支梁形式,桁架臂受轴向载荷S、自重分量的均布载荷q以及端部弯矩M0的共同作用。
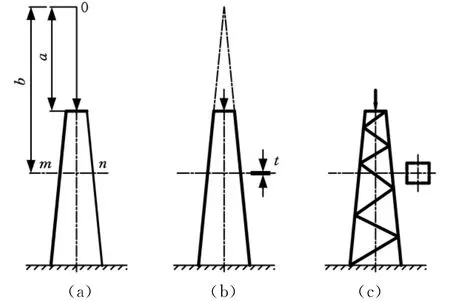
图2 不同结构形式臂架示意图
横向均布载荷q大小为

式中,l为臂长名义尺寸,为桁架臂根部铰点与起升滑轮铰点距离,一般设计为整数。
则桁架臂力学模型可以简化为图3所示的简支梁结构形式。
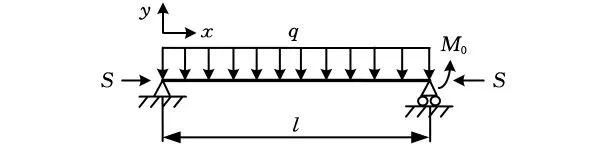
图3 桁架臂简化力学模型图
由铁摩辛柯弹性稳定性理论可推知下面两个方程。
(1)由力偶引起的梁—柱压弯挠曲方程。如图4所示,简支梁受轴向力S与端部力偶作用,则y向产生的位移y1为
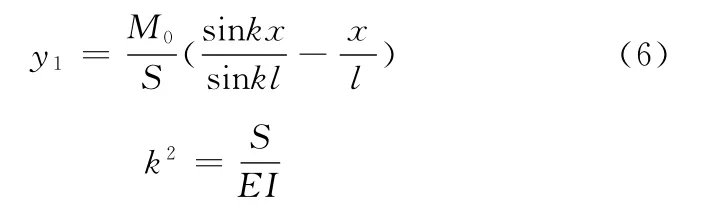
式中,E为弹性模量;I为截面惯性矩。

图4 力偶引起的梁—柱弯曲图
(2)由均载引起的梁—柱压弯挠曲方程。如图5所示,简支梁受轴向力S与均载q作用,则y向产生的位移y2为
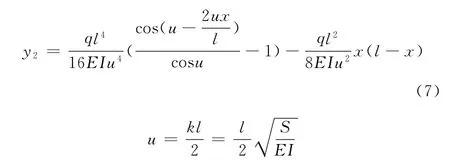
则桁架臂实际挠曲方程为

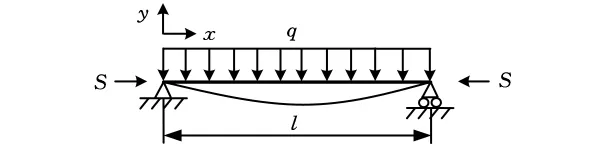
图5 均载引起的梁—柱弯曲图
1.4 能量法在铰点布局设计中的应用
在弹性材料体内,如果略去加载和卸载过程中的能量损耗,外力所做的功在数值上就等于积蓄在弹性材料体内的应变能。
对于一个结构单元,整体应变能高的时候,应力会处于较高的状态。所以从宏观角度来看,变形以及应力可以体现在结构整体或者单元的应变能上。故本文中,以整体结构最小屈曲储存应变能这一量化指标作为评判铰点布局设计合理性的标准。
1.5 桁架顶节部铰点布局优化数学模型
以屈曲储存应变能最小为目标,以顶节铰点位置上下限为约束,对桁架臂顶节铰点布局进行优化设计。
桁架臂屈曲储存应变能方程:
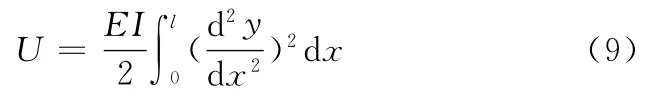
如图6所示,以桁架臂轴线方向为x′坐标,过起升滑轮铰点且垂直于桁架臂轴线方向为y′坐标,建立局部坐标系。

图6 顶节铰点位置可行域
可知,起升滑轮铰点坐标P1∈Ω1,拉索铰点坐标P2∈Ω2。这里
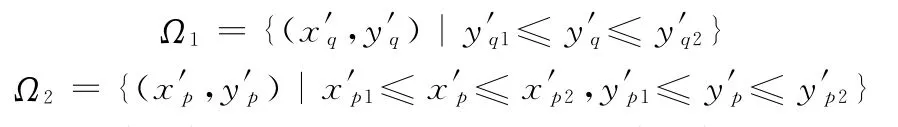
且根据工程实际中安装等需要,两滑轮距离要满足:

式中,d0为两滑轮最小安装距离。
因此,该优化模型可最终表示为

2 桁架臂受力影响因素分析
桁架臂结构整体主要受起吊过程中工作工况状态的不同以及各铰点位置的具体布置情况等影响,集中体现于桁架臂实际所受轴向力及端部弯矩的大小。因此,分析不同工况及顶节铰点位置的布局对桁架臂轴向力及端部弯矩的影响,有利于确定典型工况、探寻各铰点对桁架臂受力影响大小。
2.1 桁架臂受力典型工况的选取
以某150t桁架臂起重机为例,其顶节各铰点如图6所示。该型号起重机顶节起升滑轮铰点坐标与拉索铰点局部坐标分别为(0,y′q),(x′p,y′p)。其数值大小为:y′q= -477mm;x′p= -200mm,y′p=608mm。桁架臂轴向力S及端部弯矩M0随桁架臂仰角θ及起重量Q变化情况如图7所示。

图7 桁架臂轴向力和端部弯矩变化趋势图
分析可知:①该型号起重机最小臂架轴向力及最小端部弯矩工况出现在桁架臂为仰角45°左右的时候;②桁架臂轴向力及端部弯矩随起重量的增加呈现非规律性变化。
因此,可选择几个不同角度、吊载不同起重量工作工况作为典型工况,分别对其桁架顶节部铰点位置布局进行优化,探寻其优化结果的不同。
2.2 铰点位置对桁架臂受力影响分析
对于选定的典型工况,桁架臂轴向力S与端部弯矩M0随顶节各铰点位置坐标的不同呈现规律性变化:
(1)由图8可知,在起升滑轮铰点坐标值确定的情况下,轴向力及端部弯矩随拉索铰点纵坐标的增加而递减,而随横坐标的增大先递增后递减。
(2)由图9可知,在拉索铰点坐标值确定的情况下,起升滑轮铰点纵坐标值越大,其轴向力越小,而端部弯矩值反而增大。
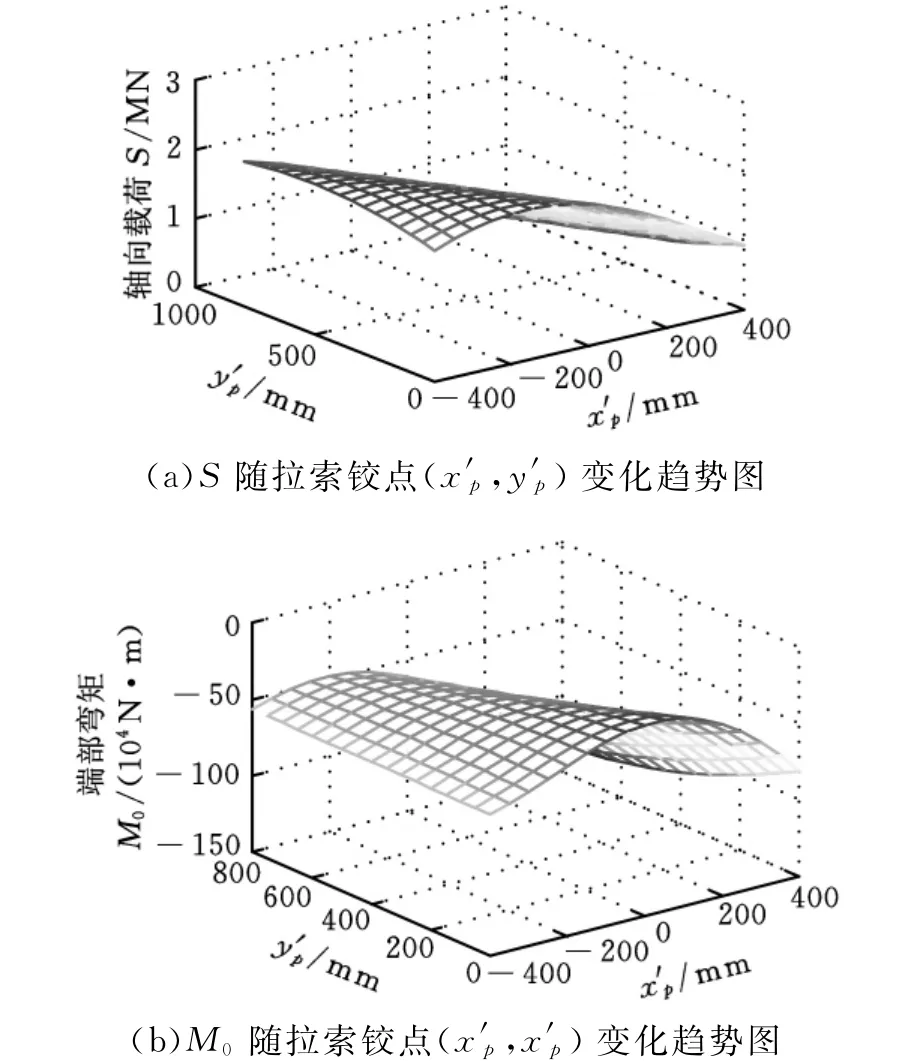
图8 桁架臂轴向力和端部弯矩变化趋势图
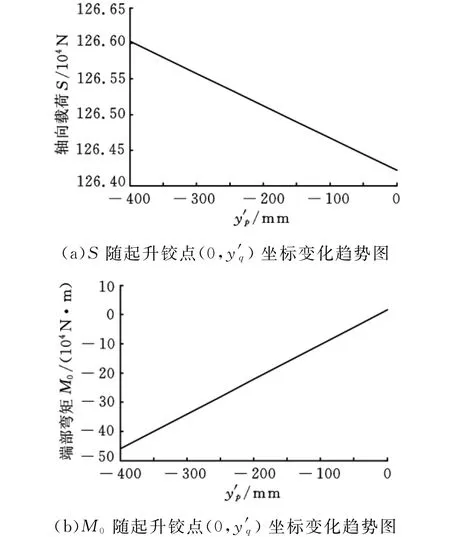
图9 桁架臂轴向力和端部弯矩变化趋势图
由上述变化规律可知,桁架臂轴向力与端部弯矩随顶节铰点位置坐标的变化呈现非严格递增或递减趋势。优化问题最优解很可能不在边界处得到,需要寻找合适的算法对可行域进行搜索求得。
3 优化问题的求解
3.1 优化算法的选择
遗传算法具有全局寻优的能力,能够解决复杂的优化设计问题。但常规的遗传算法容易陷入局部最优,需要对其进行改进,下面介绍常见的改进方法。
3.1.1 自适应交叉和变异概率
遗传算法中交叉概率Pc和变异概率Pm的选择是影响遗传算法行为和性能的关键所在,直接影响算法的收敛性。Pc过大,新个体产生的速度过快,会导致遗传规模被破坏的可能性变大。但如果Pc过小,会使搜索速度缓慢,甚至停滞不前。对于变异概率Pm,如果Pm过小,不易产生新的个体;如果Pm取值过大,遗传算法就变成了纯粹的随机搜索算法。自适应遗传算法在保持群体多样性的同时,能保证遗传算法的收敛性。经过改进后的Pc和Pm的计算表达式可参见文献[12]。
3.1.2 小生境适应度共享函数
在标准遗传算法(SGA)中,交配完全是随机的,虽然这种随机化的杂交形式在寻优的初始阶段保持了解的多样性,但在进化后期,大量个体集中于某一极值点上,其后代就造成了近亲繁殖。
为避免上述现象的产生,常运用小生境适应度共享函数代替原有的个体适应度值,其基本做法如下:通过表征个体之间相似程度的共享函数(表示群体中两个个体之间关系密切程度的函数)来调整群体中各个体的适应度,从而在群体的进化过程中,依据调整后的新适应度来进行选择操作,以便维护群体的多样性,创造出小生境的进化环境。共享函数的表达式参见文献[13]。
3.1.3 几种常见算法对比分析
依据上述改进方法,本文分别用标准遗传算法(SGA)、自适应遗传算法(AGA)、小生境遗传算法(NSGA)、自适应小生境遗传算法(NAGA)求解铰点优化问题,优化目标函数为臂架强度应力公式,其优化结果如表1所示,优化图解如图10所示。
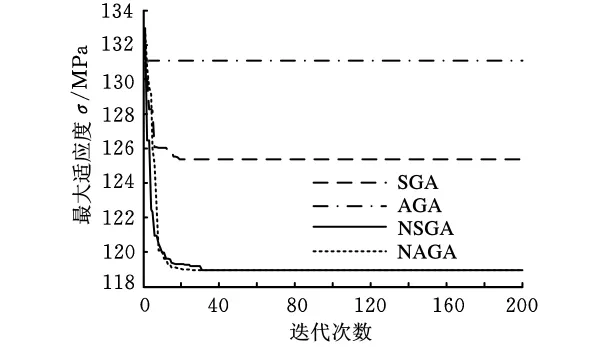
图10 四种优化算法优化图解
结果表明:①NSGA、NAGA优化结果优于SGA、AGA优化结果,但计算效率较之更低;②NAGA优化效率强于NSGA优化结果,收敛性更强。
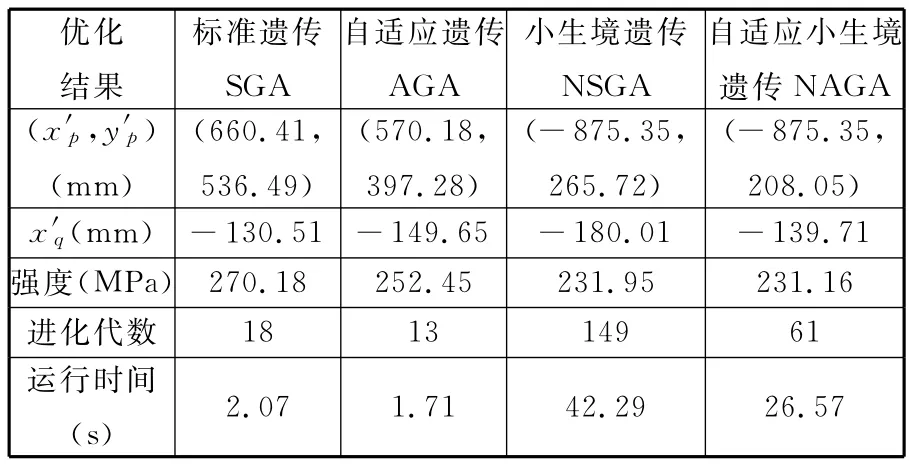
表1 四种优化算法优化结果对比
考虑到工程实际要求,本文选取自适应小生境遗传算法为本文的最终优化算法,其优化结果更好、收敛性更强,计算效率也能满足要求。
3.2 问题求解
以某150t桁架臂起重机为例,选取该起重机典型工况如表2所示。基于自适应小生境遗传算法进行优化设计,取群体大小为200,交叉概率Pc=0.8,变异概率Pm=0.08,基因型与表现型Niche半径分别取σr1=3,σr2=0.005。
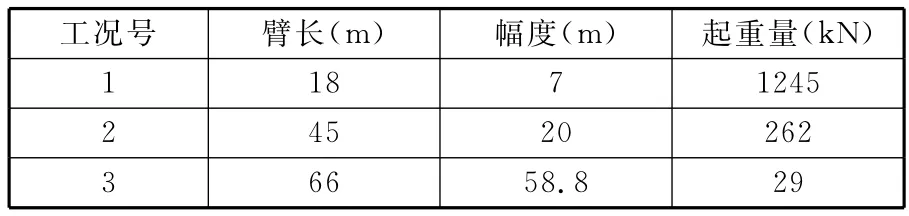
表2 150t桁架臂起重机典型工况
针对表2中工况,在MATLAB中编写遗传算法求解优化问题,优化结果如表3所示。
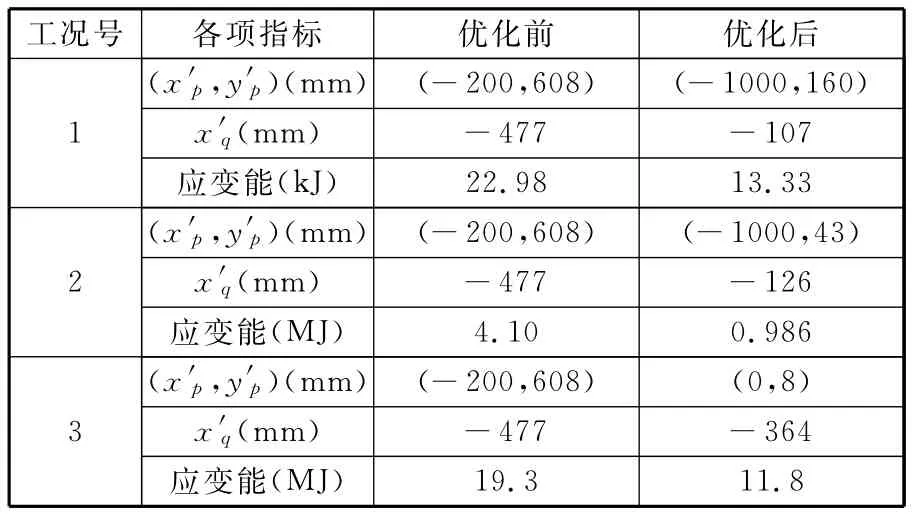
表3 三种典型工况下最优解
由表3可知:优化后臂架结构整体应变能较之前得以大大降低,优化后臂架结构总体应变能处于较低能级状态;铰点位置最优解随工况的变化而变化。
工程实际中,可根据需要选取关键性的代表性工况进行优化问题求解(例如,臂架结构对于工况1有较高要求,则优化目标函数可选择为该工况下其整体应变能),也可以选择多个典型工况以各个工况应变能的加权之和为目标函数进行求解(例如,臂架结构对于工况1、工况2、工况3均有较高要求,则优化目标函数可选择为三种工况下其整体应变能的加权之和)。
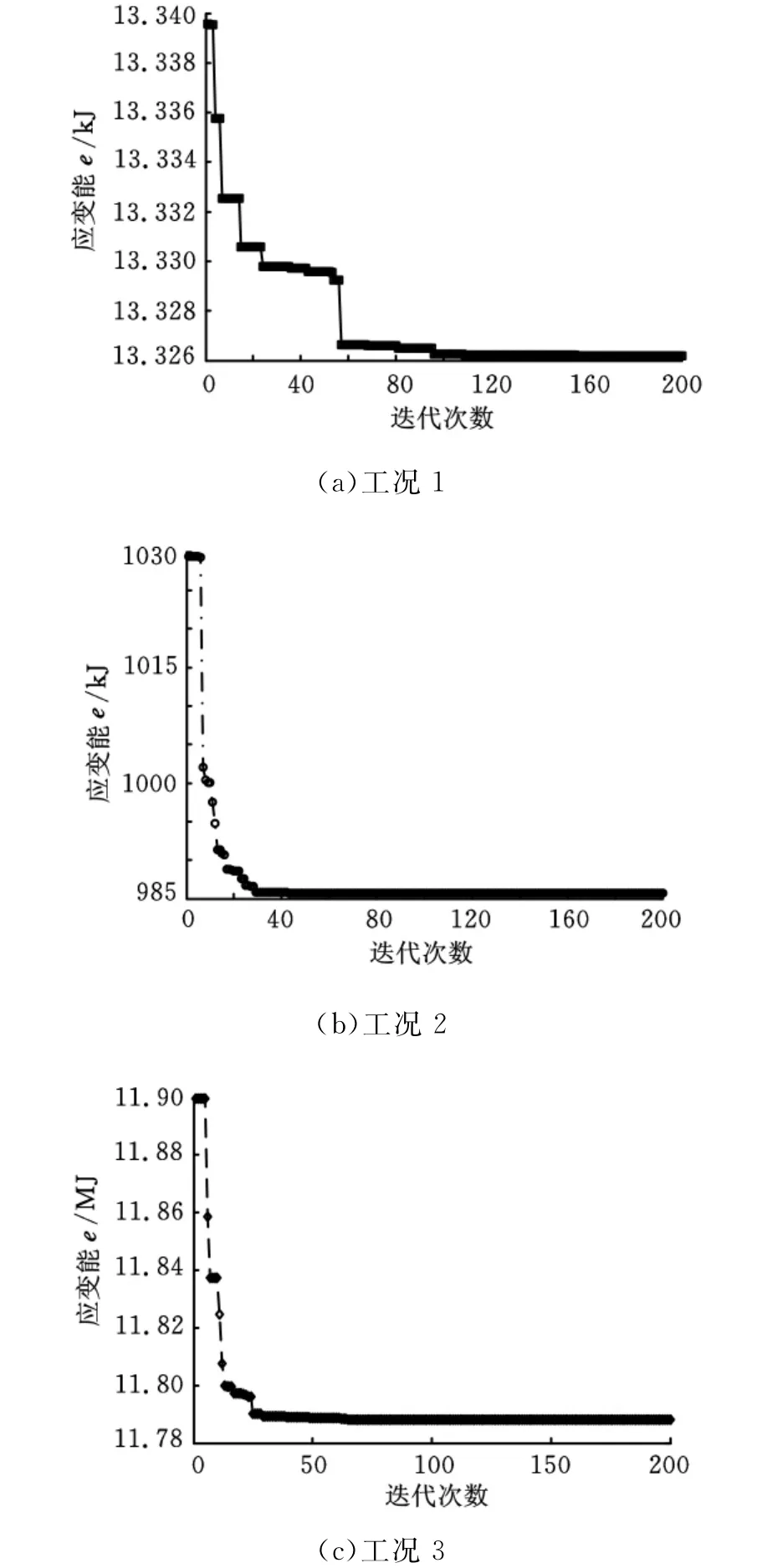
图11 三种典型工况下最优图解
4 优化结果对比分析
针对上述优化结果,分析比较吊臂整体稳定性。具体表达式参见文献[14]。由此计算出的轴向力、弯矩及整体稳定性应力的对比如表4所示。
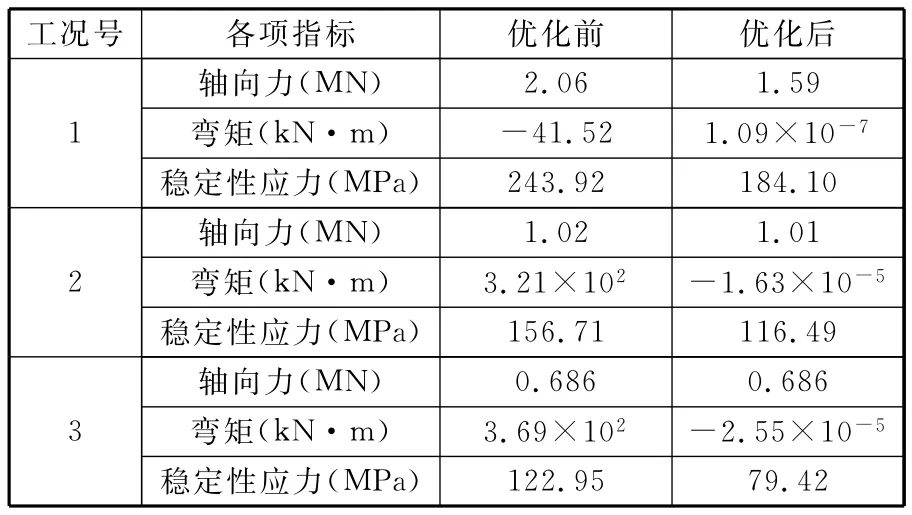
表4 优化前后桁架臂整体稳定性应力对比
优化前后结果对比分析表明:优化后桁架臂整体稳定性得到改善,轴向力减小,端部弯矩大幅降低。
5 结论
(1)将铁摩辛柯弹性梁理论运用于铰点优化设计过程中,通过实际算例验证,在优化结果上取得了满意的表现。
(2)提出了以顶节铰点位置坐标上下限及铰点距离大小为约束条件,以结构整体最小屈曲储存应变能为目标函数的数学模型,优化结果分析表明其合理性。
(3)通过将遗传算法应用于铰点位置布局优化当中,并运用自适应小生境的思想对其进行改进,求解工程实际中的结构组合优化问题。
(4)该方法除可以应用于桁架臂结构铰点布局优化,还可以为其他形式细长梁铰点布局提供设计依据。
[1]徐格宁.机械装备金属结构设计[M].北京:机械工业出版社,2009.
[2]张质文,虞和谦,王金诺,等.起重机设计手册[M].北京:中国铁道出版社,1998.
[3]Llu_õs G,Antoni A.Shape and Cross-section Optimization of a Truss Structure[J].Computers and Structures,2001(79):681-689.
[4]魏文儒,屈福政.基于ANSYS的空间桁架结构拓扑优化设计[J].起重运输机械,2008:32-34.Wei Wenru,Qu Fuzheng.Topology Optimization of Space Truss Structure Based on ANSYS[J].Hoisting and Conveying Machinery,2008:32-34.
[5]Yang Wei,Wang Jiaxu.Investigation Experimental Sensitivity of Work Device Natural Frequency of Hydraulic Excavator[J].Transactions of the Chinese society of Agricultural Machinery,2006,37(2):21-24.
[6]Han Jun,Chen Gaojie.Mechanical Property Analysis of Four-freedom Excavating Device[J].Journal of PLA University of Science and Technology,2010,11(3):290-295.
[7]蒋炎坤,刘刚强.基于遗传算法的挖掘机工作装置铰点位置优化[J].华中科技大学学报,2011,39(3):22-25.Jiang Yankun,Liu Gangqiang.Optimization of Hinge Position for Working Device of Excavators by Genetic Algorithm[J].Journal of Huazhong University of Science and Technology,2011,39(3):22-25.
[8]Timoshenko S P,Gere J M.Theory of Elastic Stability[M].New York:MoGraw-Hill Book Company,Inc.,1985.
[9]马恒,刘栋栋.基于遗传算法的桁架结构布局优化设计[J].北京建筑工程学院学报,2005,21(1):68-71.Ma Hen,Liu Dongdong.Layout Design Optimization of Truss Structures Using Genetic Algorithm[J].Journal of Beijing Institute of Civil Engineering and Architecture,2005,21(1):68-71.
[10]Sachin M,Paolo G.Reliability-based Optimal Design of Electrical Transmission Towers Using Multi-objective Genetic Algorithms[J].Computer-Aided Civil and Infrastructure Engineering,2007,22:282-292.
[11]Vedat T,Ays_T D.An Improved Genetic Algorithm with Initial Population Strategy and Self-adaptive Member Grouping[J].Computers and Structures,2008,86:1204-1218.
[12]魏立新,李兴强.基于自适应遗传算法的冷连轧负荷分配优化[J].中国机械工程,2009,20(20):2506-2509.Wei Lixin,Li Xingqiang.Load Distribution Optimizationin Tandem Cold Rolling Based on Adaptive Genetic Algorithm[J].China Mechanical Engineering,2009,20(20):2506-2509.
[13]刘爱军,杨育.含精英策略的小生境遗传退火算法研究及其应用[J].中国机械工程,2012,23(5):556-563.Liu Aijun,Yang Yu.Research on Niche Genetic Annealing Algorithm with Elite Strategy and Its Applications[J].China Mechanical Engineering,2012,23(5):556-563.
[14]徐克晋.金属结构[M].北京:机械工业出版社,1993.
- 中国机械工程的其它文章
- 基于信号共振稀疏分解的转子早期碰摩故障诊断方法

