环冷机组TSP无组织排放溯源及影响因素分析

王 伟，周璀巍，杨海真，

(1.同济大学环境科学与工程学院环境管理研究所，上海 200092;2.同济大学教育部长江水环境实验室，上海 200092)

烧结是将各种粉状含铁原料，配入适量的燃料和熔剂，加入适量的水，经混合和造球后在烧结设备上使物料发生一系列物理化学变化，将矿粉颗粒黏结成块的过程。它不仅是钢铁工业中一个物流量巨大的环节，也是一个有着高污染排放系数的环节［1］。经研究表明烧结TSP无组织排放在烧结厂总TSP污染排放中占很重要的部分，特别是在烧结矿的冷却过程中。国内普遍采用的是鼓风环形冷却设备通过鼓风来冷却烧结矿，在这个过程中大量的矿物粉尘颗粒物会伴随着热烟气排放到空气中［2］。这部分无组织粉尘会夹带大量的Cl－离子、铁、氨、Pb等有害物质排放到空气中，严重影响工作环境以及工人们的身体健康。因此对无组织粉尘无组织排放规律的研究对实现烧结厂的清洁生产以及保护工人们的身体健康都有十分重要的意义。

目前国内对于烧结污染物的控制主要集中在对其有组织排放的烟尘进行脱硫和减量化处理，而国外很多学者如Dany Hleis等对钢铁行业无组织粉尘的研究则主要集中在其污染物化学特征的识别［3］。同时目前颗粒物面源的反推模式相较于纯气质模型而言还不够成熟，关于颗粒物的面源计算模式也只是处于理论研究阶段，在工程应用上的相关报道也极少，因而在实际操作中我们很难得到这部分无组织污染物的排放量［4］。这就使得对无组织污染源减量化措施的比选没有一个直接的量化的参考。本研究刚好弥补了这方面研究的空白，以某钢铁企业的烧结厂3号烧结机为例，以中心虚点源法为基础对环冷机TSP无组织排放源强推算方法及其误差进行了分析研究，从而为颗粒物面源模式的反推计算提供了参考。对厂区内小范围无组织排放源排放规律的研究具有一定的借鉴意义。

1 实验部分

1.1 实验仪器及材料

本实验采用的仪器与材料包括:KC－120H型智能中流量 TSP采样器、电子分析天平(XB120A)、智能型风速风量仪 (MODEL6036)、激光粒度仪 (Mastersizer 2000)、皮尺、锡箔纸。

1.2 采样方法

根据《大气污染物无组织排放监测技术导则》HJ/T55－2000，结合现场气象监测结果，选取在西北风为主导风向时进行监测。在上风向布置一个参照点，下风向位置布置3个监测点。具体监测点位布置如图1所示，在烧结厂西北部设置一个参照点其距环冷中心的距离为49m，东南部设置渐远的3个参照点1、2、3，其距环冷机中心的距离分别为48m、62m、82m。采样器进样口距地面1.5m。

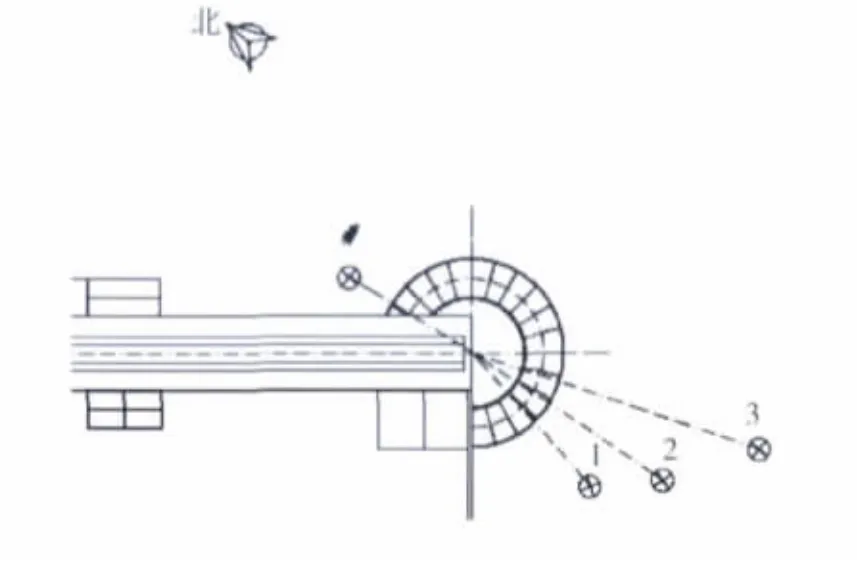
图1 监测点位布置图Fig.1 The layout of the monitoring sites

由于受到采样条件的限制，在采样频率上对导则规定进行了调整。实行多小时连续采样，再取平均值，以平均的小时浓度代表监测点的日均浓度。每次监测从监测当天的上午8点开始至下午2点，每换一次滤纸，并记录下当次气体采集的体积、温度。从2012年11月7日到2013年1月17日测得有效监测日期10天。

1.3 样品分析

采集TSP所用滤膜在使用前均在X光片机上进行检查，保证不存在任何缺陷，样品采集后用镊子取下滤膜，将滤膜对折，采样面向里对折，并用铝箔纸包裹后放入滤膜袋，存放于4℃冰箱内［5］。采样完成后，分别按照《总悬浮颗粒物的测定－重量法》GB/T15432－1995和《粉尘物性试验方法》GB/T 16913－2008所的规定方法，确定样品的TSP浓度和粒径分散度。

2 模拟计算

2.1 模型及参数的选取

目前对面源扩散模式进行模拟最常用的是后置虚点源法，该法广用于在建筑物附近的排放和工厂车间的无组织排放［3］，但是该法对于边长小于500m的面源模拟效果很不理想［3，4］。因此根据环冷机组本身构型的特点本次实验选用中心虚点源法来模拟计算。中心虚点源是后置点源法的一个修正方法，即在面源中心虚设一个点源，在扩散模拟的过程中加一个初始的烟云分布，利用经验公式将面源转化为特殊的线源来进行计算［6，7］。研究按照国标推荐的方法将面源虚拟成一个位于环冷机形心的点源，并用修正后的点源扩散模型对环冷机的排放强度进行模拟。同时考虑颗粒物干沉降的影响，在计算时对有效源高进行修正［8］。由于本研究的对象是粉尘颗粒物，主要是以干沉降的方式迁移到地面，因此在反推计算的过程中还必须考虑不同粒径颗粒物具有的不同干沉降速率［9］。

根据高斯模式的基本形式，在有风气象条件下，面源下风向地面污染物浓度采用经过面源修正的部分反射倾斜烟云模型，具体的计算表达式如式(1)所示［9，10］:

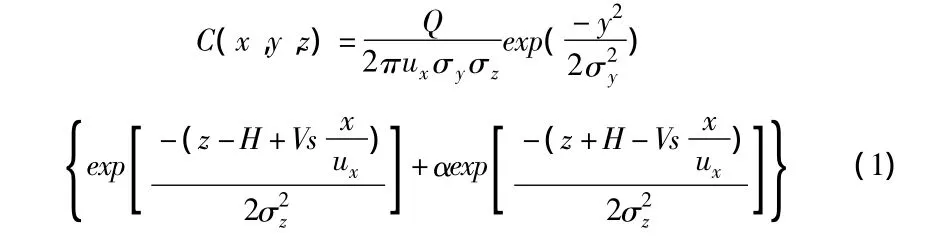
式中:

C(x，y，z)－ 颗粒物在坐标为(x，y，z)处浓度，g/m3;

Q－颗粒物排放源浓度，g/s;

α－地面反射系数;

ux－计算方向上的平均风速，m/s;

H－有效源高，m;

vs－颗粒物干沉降速率，m/s;

σy－修正后的横向扩散参数;

σz－修正后的铅直方向扩散参数。

根据GB/T 3840－91《制定地方大气污染物排放标准技术方法》中关于面源垂直向和横向扩散参数幂函数表系数取值表所得的扩散参数表达式，对横向扩散参数进行经验公式的修正后［11］，得到在D类大气稳定度下环冷机面源的横向扩散表达

式为:σy=0.234x0.93+垂直向扩散参数表达式为:σz=0.221x0.83。其他计算参数参照《环境影响评价技术导致—大气环境》HJ/T2.2－200进行选取［11，12］。

2.2 源强的计算

由于不同粒径段的颗粒物在空气中沉降时具有不一样的沉降速率，因为它们在大气中的扩散规律也不相同。在实际反推计算时需要分粒径范围分别对源强进行反推计算。因此本实验在模拟反推源强时将TSP源强分了5个粒径段 (0～15μm、15～30μm、31～47μm、48～75μm、76～100μm)来分别进行反推计算。其具体计算过程如下:

在不同的粒径段分别预设一系列源强，通过扩散公式分别计算出每个预设源强在3个监测点的产生的污染物浓度。将每组估算值分别与实测值进行误差分析。对于每个粒径段而言，当3处的平均误差最小时对应的预设源强即为此粒径段的源强。

将每个粒径段的平均误差分别乘上各部分占总排放量的比例系数后，加和到总平均误差，本实验通过对总平均误差的分析来确定估算模型的准确度。

3 结果与分析

3.1 粒径分布特征

在各个监测位点不同粒径段所占体积百分比如图2所示。

从图2中可发现，对于总悬浮颗粒物，0～30μm的小颗粒物所占体积组成较大，一般超过50%;参照点0～15μm所占的百分比最高。对于3个监测点而言，0～30μm粒径段所占体积比例随着距离的增加而增加;31～75μm粒径段所占比例先减小后略有增加;76～100μm粒径段所占比例随着距离的增加不断减小。

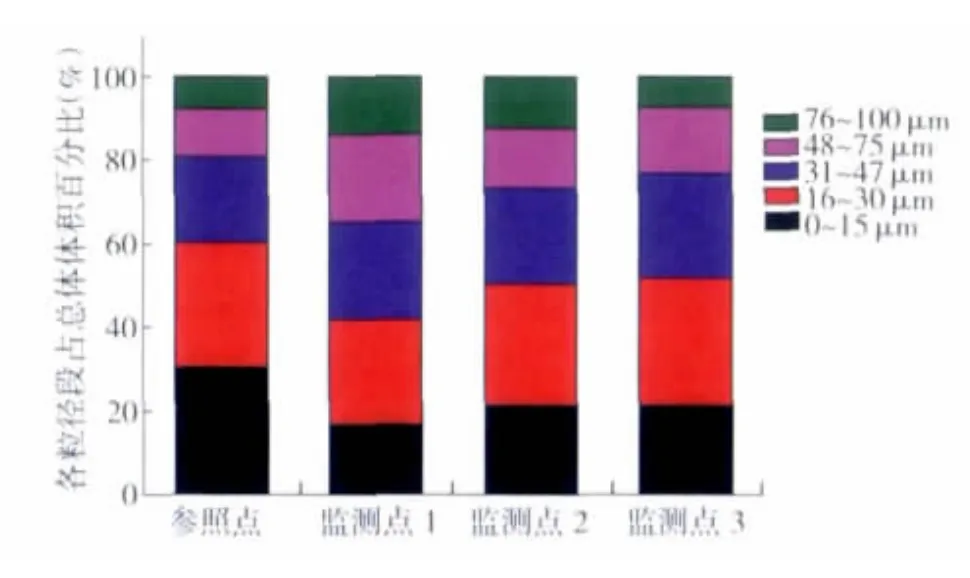
图2 各监测点颗粒物粒径体积百分比分布图Fig.2 The particle size volume percentage distribution of the various monitoring points

产生这种现象的原因是不同粒径段颗粒物的沉降系数不同，在密度相同的情况下大粒径的颗粒物会先沉降下来，从而改变整体各个粒径段的体积百分比分配。这也说明了分粒径段反推源强的必要性。

3.2 误差及源强特征

3.2.1 误差分布特征与影响因素分析

各粒径段的最小总相对物误差机和面源总误差随监测时间变化的趋势如图3所示:横坐标1～10分别对应从2012年11月7日到2013年1月17日的10个有效监测日。

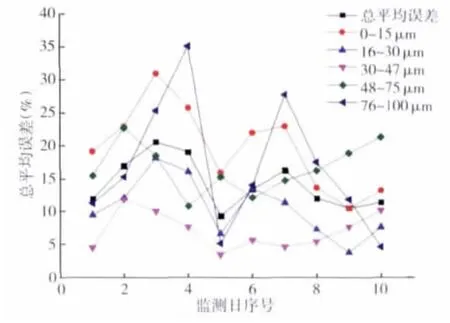
图3 10个有效监测日各粒径段误差及总平均误差分布变化图Fig.3 Particle size error and total average error distribution of 10 effective monitoring days

由图3可知，利用中心虚点源法模拟计算烧结厂环冷机组面源无组织排放的总平均误差范围在9.3% ～20.6%。其中30～47μm粒径段的总平均误差最小，误差范围在 3.4% ～11.8%;75～100μm粒径段误差范围跨度最大，4.6% ～35.1%。在第5个有效监测日 (12月5日)算得的面源总平均误差最小，只有9.3%。这与周斌斌等人关于后置点源法在不稳定大气条件下进行数值模拟时会产生10%～20%计算误差的研究结果相似［13］。

本次研究对这种系统误差浮动产生的原因进行分析，认为可能是受到了不同气象条件的影响。并将模拟计算所得计算系统误差与监测当日风速气象条件进行拟合，其拟合结果如图4所示:

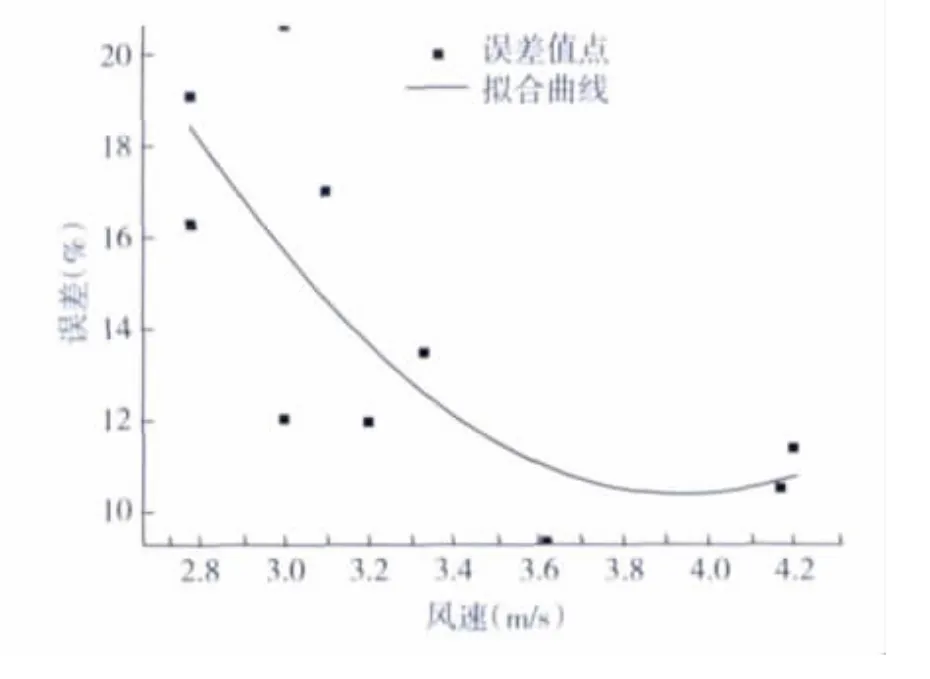
图4 模拟误差与监测当日风速拟合曲线图Fig.4 Fitting curve of simulation error versus wind speed of monitoring days

由图4可知，风速与误差之间存在很大的相关性，即随着风速的增大模拟的总平均误差呈减小趋势。因此监测时选取风速较大的时候可以减小计算反推的系统误差。对于该环冷机而言较为适宜的反推模拟风速条件为3.5～4.2m/s。

综上所述:通过误差分析我们可以发现，分不同粒径段采用中心虚点源法在不稳定大气条件下对环冷机无组织排放源进行源强推算时，会出现9.3%～20.6%的系统误差，这与前人的研究结果相似。本研究进一步对产生这种误差的原因进行了分析，发现风速与误差之间存在着很大的相关性，即通过选取较大风速的气象条件可以减小该系统误差，对于该环冷机而言较为适宜的反推模拟风速条件为3.5～4.2m/s。

3.2.2 环冷机面源的排放特征

每个有效监测日最小相对误差下，每个粒径段排放量与面源总排量如图5示。

由图5可知，该环冷机面源的无组织TSP排放量范围在12300～20790mg/s，跨度范围较大。其中在16～30μm粒径段颗粒物占的比例最大，达28%;75～100μm占的比例最小，只有14%。随着粒径尺度的增大，排放量先增大后减小，颗粒物粒径分布满足两头小中间大的趋势。

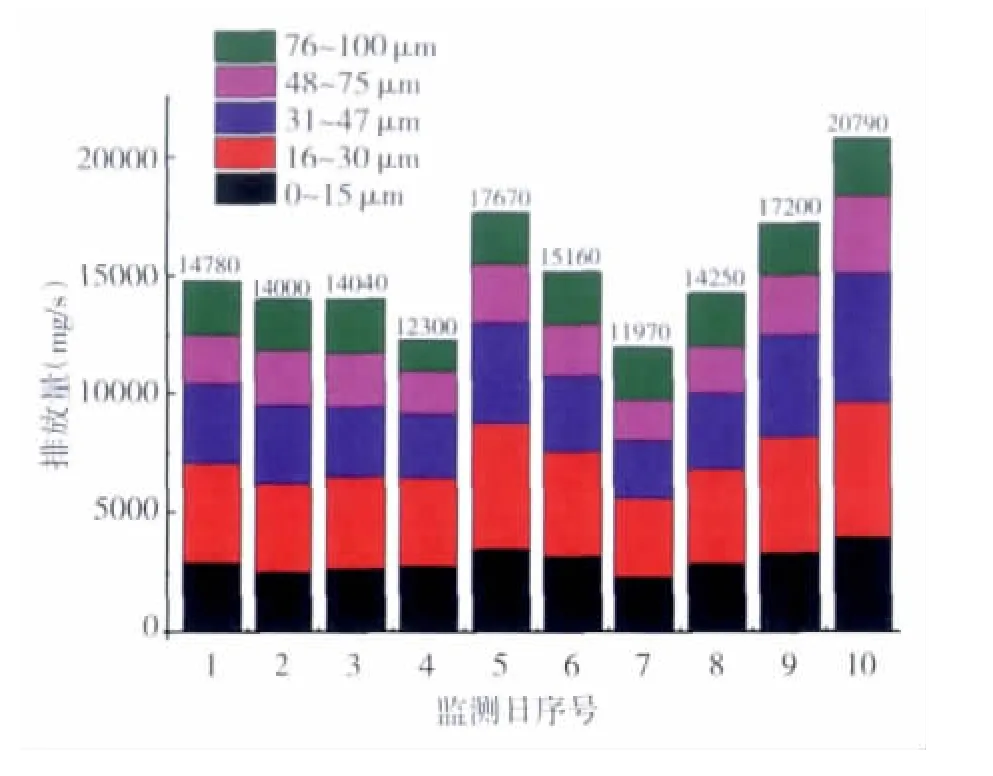
图5 10个有效监测日各粒径段排及总排放量分布图Fig.5 Each particle size segment emission and total emissions of 10 effective monitoring days

3.3 影响因素分析

采用spss软件对该烧结厂5类原料相关组分(混匀矿、烧结粉、溶剂、固体燃料、返矿)与环冷机的无组织TSP排放量进行偏相关性分析，通过多元线性拟合的方式，确定出各个排放量对于各个影响因子的偏相关性［14～16］，见下表。

表 各原料的使用量与TSP排放量多元线性回归分析结果Tab.Result of linear regression analysis of raw material usage amount and TSP emissions

由上表多元线性回归的结果可知:在所有原料中混匀矿的使用量与TSP的排放量拟合T值最大，为1.676。因此在众影响因子中混匀矿的使用量与TSP的排放量偏相关性最大，可以认为混匀矿的使用量是TSP排放的主要影响因素，但是sig值为0.169＞0.05，二者的直接线性关系不强。在实际生产中混匀矿的使用量表征着烧结厂的生产负荷，因此可推断该环冷机组粉尘无组织排放量大的根本原因是环冷机组的超负荷使用。

4 结论

4.1 通过对各检测点的粒径分析结果表明:在各监测点处0～30μm的小颗粒物所占体积组成都很大，一般超过50%。参照点0～15μm所占的百分比最高。对于3个监测点而言:0～30μm粒径段所占体积比例随着距离的增加而增加;31～75μm粒径段所占比例先减小后略有增加;76～100μm粒径段所占比例随着距离的增加不断减小。

4.2 利用中心虚点源法模拟计算烧结厂环冷机组面源无组织排放的总误差范围在9.3%～20.6%。其中30～47μm粒径段的总相对误差最小，误差范围在3.4% ～11.8%;75～100μm粒径段误差范围跨度最大，4.6% ～35.1%。在第5个有效监测日(12月5日)算得的面源总误差最小，只有9.3%。采用中心虚点源法对环冷机无组织排放源进行源强推算时存在着9.3% ～20.6%的系统误差，但是通过选取较大风速的气象条件可以减小该系统误差，对于该环冷机而言较为适宜的反推模拟风速条件为3.5～4.2m/s。

4.3 该环冷机面源的无组织TSP排放量范围在12300～20790mg/s，跨度范围较大。其中在16～30μm粒径段颗粒物占的比例最大，达28%;75～100μm占的比例最小，只有14%。随着粒径尺度的增大，排放量先增大后减小，颗粒物质量分布满足两头小中间大的趋势。

4.4 混匀矿的使用量是TSP排放的主要影响因素，推断该环冷机组粉尘无组织排放量大的根本原因是环冷机组的超负荷使用。

［1］潘 建.铁矿烧结烟气减量排放基础理论与工艺研究［D］.湖南:中南大学钢铁冶金专业，2007.

［2］朱苗勇.现代冶金学(钢铁冶金卷)［M］.北京:冶金工业出版社，2005.9.

［3］Hleis D.Fernandez-Olmo I，Ledoux F，Kfoury A，Courcot L，Desmonts T and Courcot D."Chemical Profile Identification of Fugitive and Confined Particle Emissions from an Integrated Iron and Steelmaking Plant"［J］.Journal of Hazardous Materials，2013，250:246-255.

［4］谷 清，杨新兴.面源模式数值模拟计算分析［J］.安全与环境学报，2002，2(2):10-13.

［5］HJ/T55-2000，大气污染物无组织排放监测技术导则［S］.

［6］石坚荣.大气面源模式具体应用探讨［J］.环境污染与防治，1983，8(2):10-12，30.

［7］谷 清.我国大气模式计算的若干问题［J］.环境科学研究，2000，13(1):40-43.

［8］谷 清，杨新兴，李云生.颗粒物面源模式计算方法［J］.中国工程科学，2005，7(1):41-44.

［9］谷 清，汤大钢.面源模式反扩散参数研究［J］.环境科学研究，2001，14(5):54-56.

［10］谷 清.烟气抬升公式计算对比［J］.环境科学研究，1991，4(3):25-32.

［11］谷 清.轨迹烟流模式计算方法［J］.城市环境与城市生态，2004，17(4):35-37.

［12］吴文军，丁 峰.面源模式的通用算法探讨［J］.环境科学研究，2007，20(2):118-122.

［13］周斌斌.面源模式的精度分析［J］.上海环境科学，1992，11(2):39-41.

［14］张文彬，闫 洁，等.SPSS统计分析基础教程［M］.北京:高等教育出版社，2004.9.

［15］杨维权，等.多元统计分析［M］.北京:高等教育出版社，1989.

［16］张润楚.多元统计分析［M］.北京:科学出版社，2006.